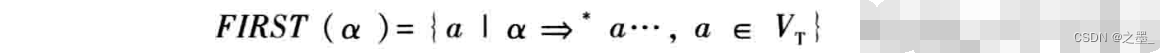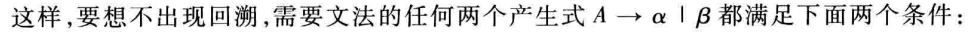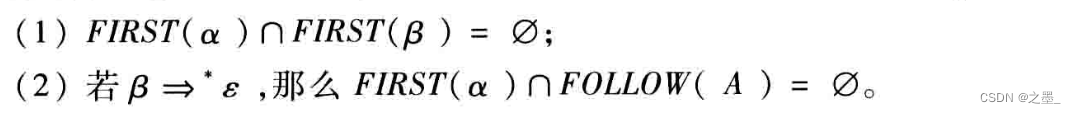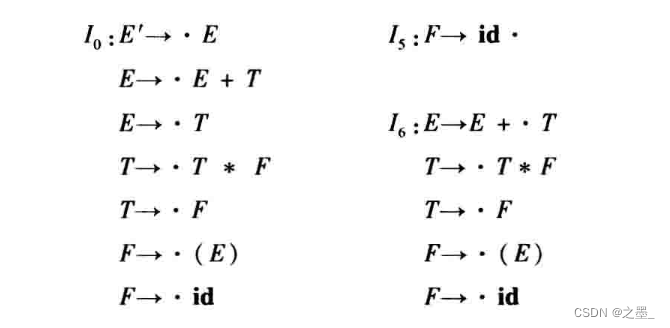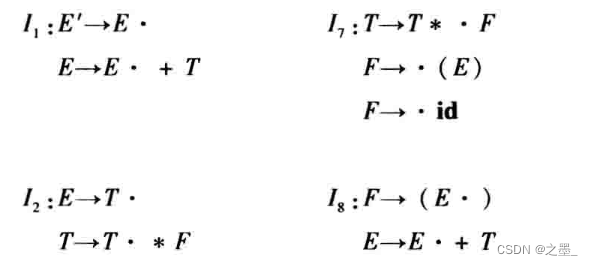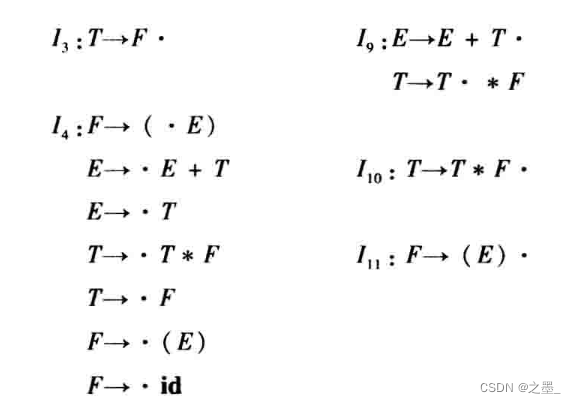系列文章戳这里👇
- 什么是上下文无关文法、最左推导和最右推导
- 如何判断二义文法及消除文法二义性
- 何时需要消除左递归
- 什么是句柄、什么是自上而下、自下而上分析
- 什么是LL(1)、LR(0)、LR(1)文法、LR分析表
- LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系
- 编译原理第三章习题
- 词法分析、构建DFA、上下文无关文法、LL(1)分析、提取正规式
- 证明LL(1)、SLR(1)、LALR(1)文法
- 翻译方案、属性栈代码
- 【运行时环境】什么是活动记录、 活动记录与汇编代码的关系
编译原理-LL(1)LR(0)LR(1)文法
了解LL(1)文法前,我们首先需要知道什么是FIRST和FOLLOW集合
FIRST集与FOLLOW集
为构造不带回溯的自上而下分析算法,首先要消除文法的左递归,并找出避免回溯的充分必要条件。消除左递归的方法已介绍了,下面讨论如何避免回溯,这就是FIRST集与FOLLOW集的工作。
在讨论不得回溯的前提对文法有什么限制之前,先定义两个和文法有关的函数。一个文法的符号串
a
a
a的开始符号集合
F
I
R
S
T
(
a
)
FIRST(a)
FIRST(a)
显然,概念定义为了保证准确性与一般性,都比较晦涩难懂,所以让我们通过一个栗子来认识这两个集合:
举个栗子
什么是LL(1)文法
把满足这两个条件的文法称为
L
L
(
1
)
LL(1)
LL(1)文法,其中的第一个
“
L
”
“L”
“L”代表从左向右地扫描输入,第二个
“
L
”
“L”
“L”表示产生最左推导,“
1
”
1”
1”代表在决定分析器的每步动作时需要向前查看下一个输人符号(即输入指针所指向的符号)。除了没有公共左因子外,
L
L
(
1
)
LL(1)
LL(1)文法还有一些明显的性质,它不是二义的,也不含左递归。
举个栗子
(
a
)
(a)
(a)证明下面文法是
L
L
(
1
)
LL(1)
LL(1)文法
S
→
A
a
A
b
∣
B
b
B
a
A
→
ϵ
B
→
ϵ
S→AaAb|BbBa\\ A→\epsilon\\ B→\epsilon
S→AaAb∣BbBaA→ϵB→ϵ
根据
L
L
(
1
)
LL(1)
LL(1)文法定义
F
i
r
s
t
(
A
a
A
a
)
=
{
a
}
,
F
i
r
s
t
(
B
b
B
b
)
=
{
b
}
First(AaAa)=\{a\},First(BbBb)=\{b\}
First(AaAa)={a},First(BbBb)={b}
F
i
r
s
t
(
A
a
A
a
)
∩
F
i
r
s
t
(
B
b
B
b
)
=
ϕ
First(AaAa)∩First(BbBb)=\phi
First(AaAa)∩First(BbBb)=ϕ,所以该文法是
L
L
(
1
)
LL(1)
LL(1)文法。
再举个栗子
构造下面文法的
L
L
(
1
)
LL(1)
LL(1)分析表
S
→
a
B
S
∣
b
A
S
∣
ϵ
A
→
b
A
A
∣
a
B
→
a
B
B
∣
b
F
i
r
s
t
(
S
)
=
{
a
,
b
,
ϵ
}
F
i
r
s
t
(
A
)
=
{
a
,
b
}
F
i
r
s
t
(
B
)
=
{
a
,
b
}
F
o
l
l
o
w
(
S
)
=
{
$
}
F
o
l
l
o
w
(
A
)
=
{
a
,
b
,
$
}
F
o
l
l
o
w
(
B
)
=
{
a
,
b
,
$
}
S→aBS|bAS|\epsilon\\ A→bAA|a\\ B→aBB|b\\ \ \\ \ \\ \begin{aligned} First(S)&=\{a,b,\epsilon\}\\ First(A)&=\{a,b\}\\ First(B)&=\{a,b\}\\ Follow(S)&=\{\$\}\\ Follow(A)&=\{a,b,\$\}\\ Follow(B)&=\{a,b,\$\}\\ \end{aligned}
S→aBS∣bAS∣ϵA→bAA∣aB→aBB∣b First(S)First(A)First(B)Follow(S)Follow(A)Follow(B)={a,b,ϵ}={a,b}={a,b}={$}={a,b,$}={a,b,$}
| a a a | b b b | $ $ $ | |
|---|---|---|---|
| S S S | S → a B S S→aBS S→aBS | S → b A S S→bAS S→bAS | S → ϵ S→\epsilon S→ϵ |
| A A A | A → a A→a A→a | A → b A A A→bAA A→bAA | |
| B B B | B → a B B B→aBB B→aBB | B → b B→b B→b |
什么是LR(0)文法
L
R
(
0
)
LR(0)
LR(0)分析法是其他
L
R
LR
LR分析法构造的基础,
L
L
L表示从左往右扫描,
R
R
R表示反向构造出一个最右推导,
k
k
k表示向前看
k
k
k个字符,缺省为
1
1
1。
如何判断:如果文法G的LR(0)分析表项没有多重定义—即动作冲突;或者它的LR(0)项目规范族中的任一状态不能同时含有移进和归约的LR(0)项目,那么文法G是LR(0)的,
举个栗子
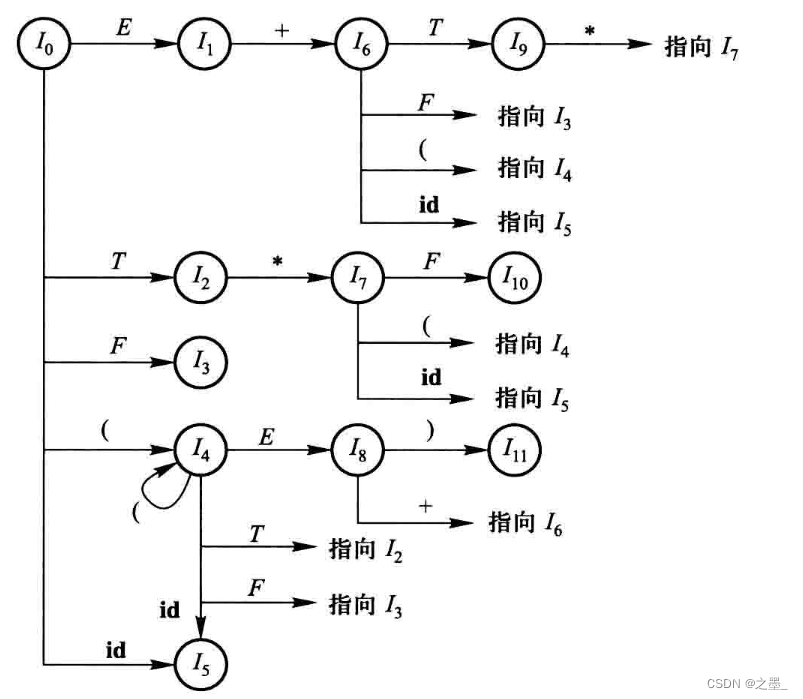
对于这个文法,它的LR(0)项目集规范族为:
上述项目集族的状态转移图为:
什么是LR(1)文法
构造 L R ( 1 ) LR(1) LR(1)项目集规范族的方法本质上和构造 L R ( 0 ) LR(0) LR(0)项目集规范族的方法是一样的,只需要修改 c l o s u r e closure closure函数和 g o t o goto goto函数。也就是LR(1)项目集在进行产生式归约时,只前看一个符号,也就是FOLLOW集中的第一个符号,若下一个符号与之匹配才进行归约。
举个栗子
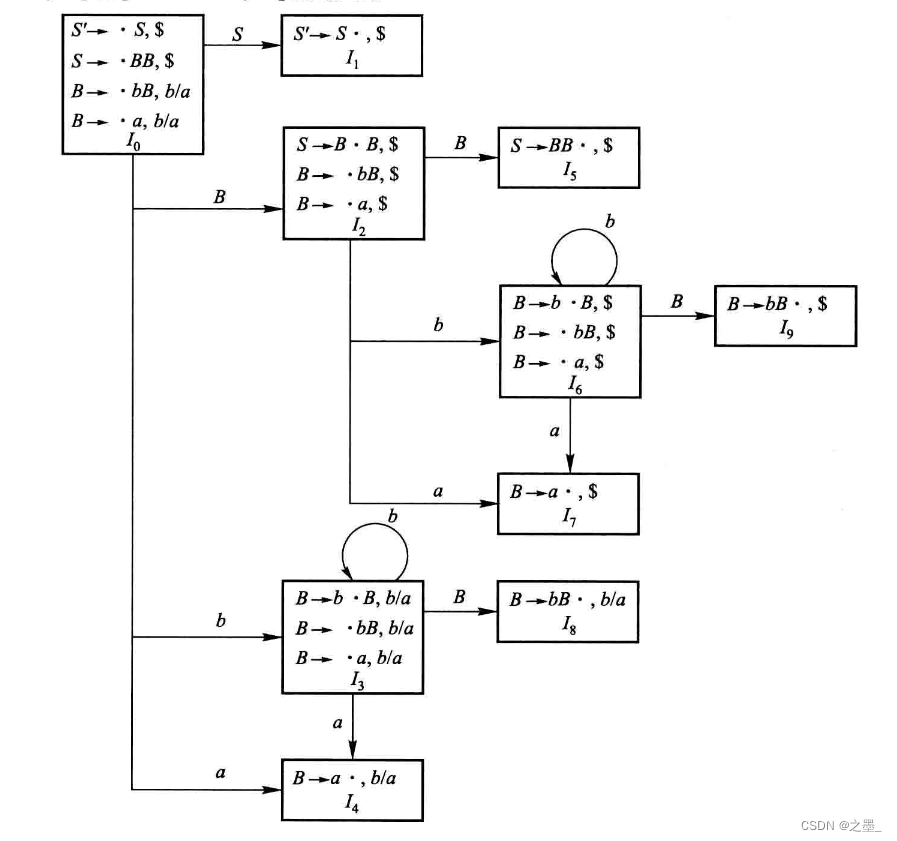
以下是该文法的
L
R
(
1
)
LR(1)
LR(1)项目集规范族以及 状态转换图
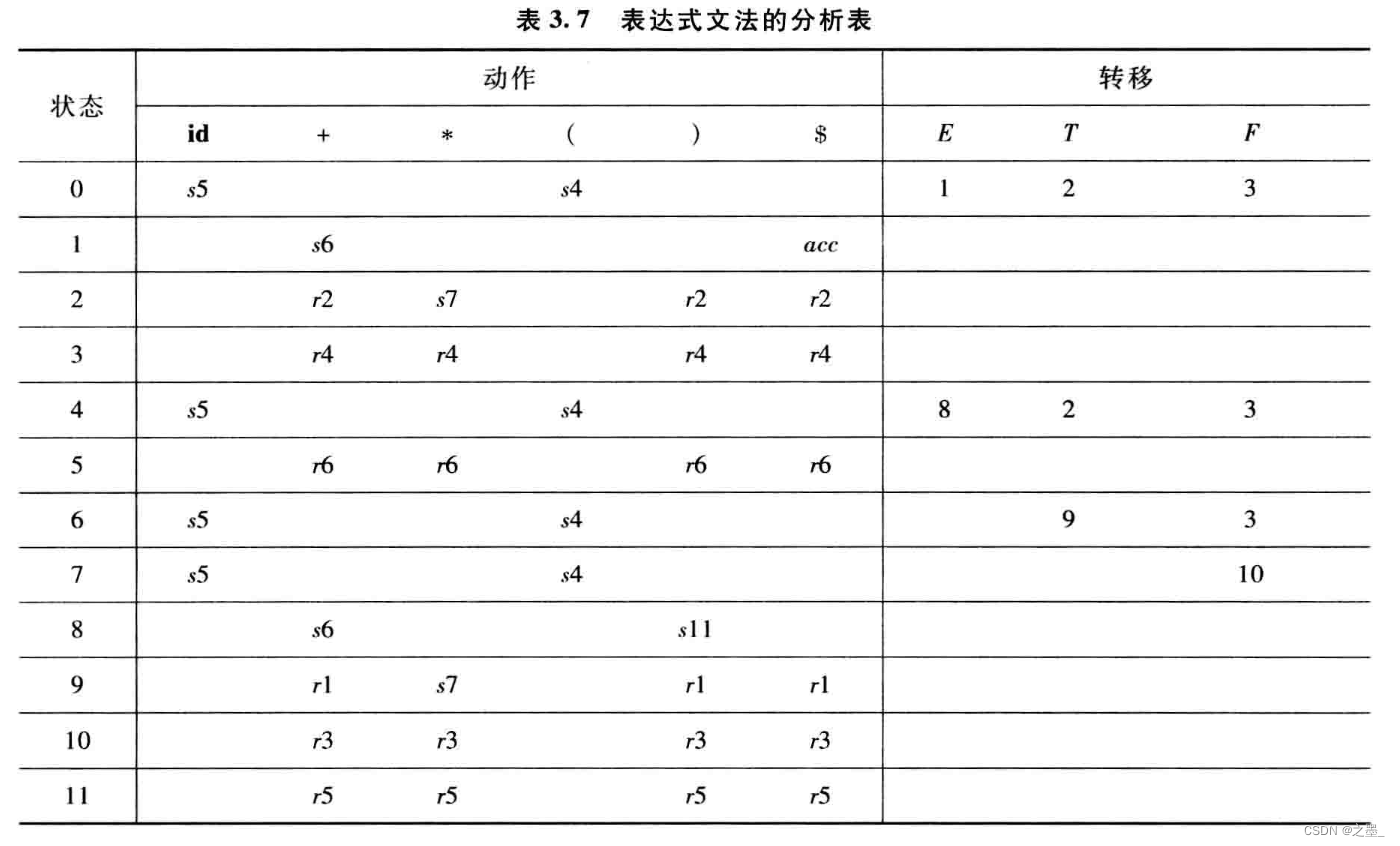
以下是该文法的规范
L
R
LR
LR分析表
LR分析表