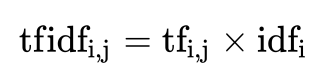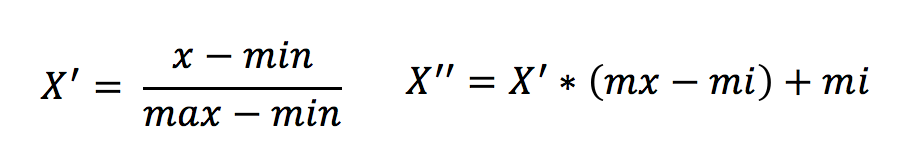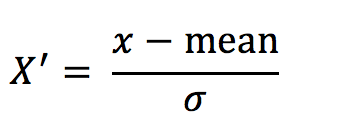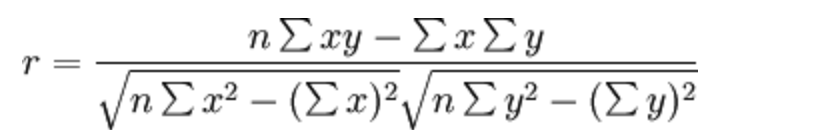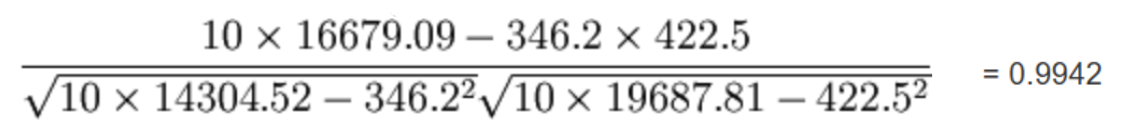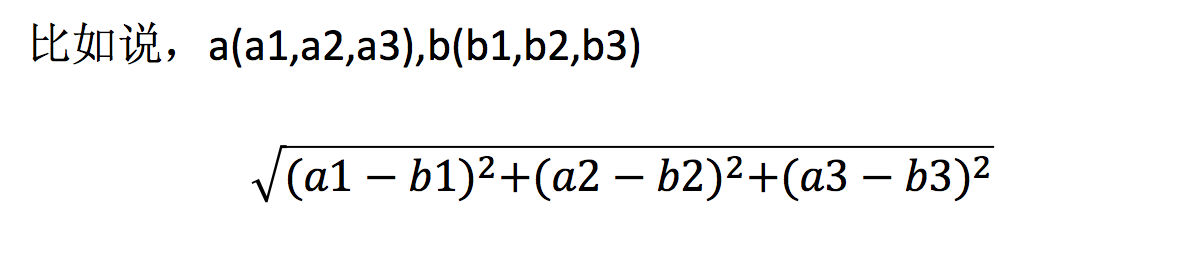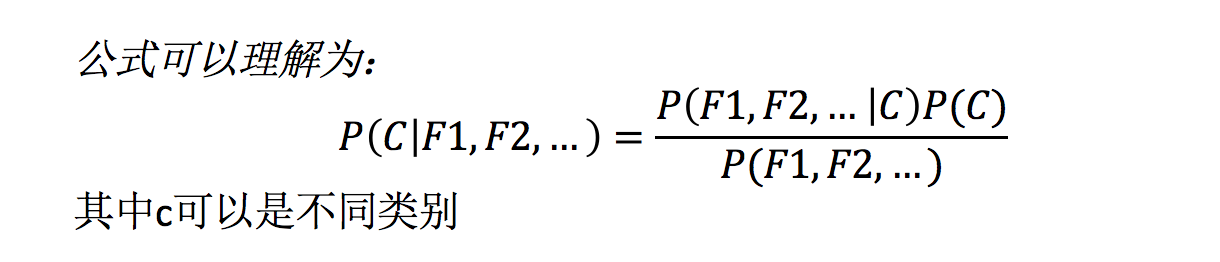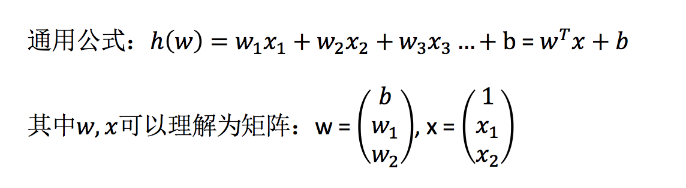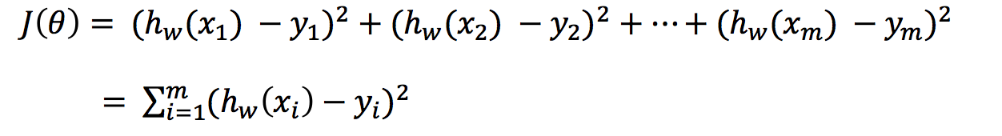文章目录
机器学习概述
1.1 人工智能概述
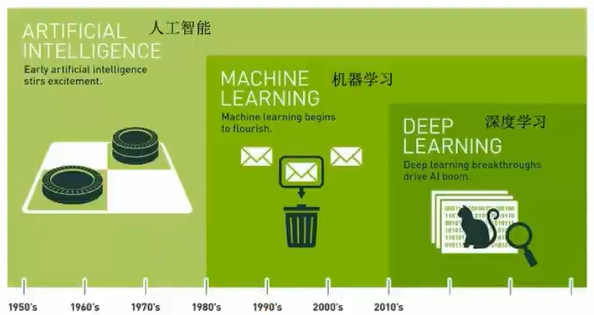
机器学习与人工智能、深度学习
- 机器学习与人工智能、深度学习的关系
- 机器学习是人工智能的一个实现途径
- 深度学习是机器学习的一个方法发展而来
- 达特茅斯会议-人工智能的起点
- 1956年8月,在美国汉诺斯小镇宁静的达特茅斯学院中,约翰·麦卡锡(John McCarthy)、马文闵斯基(Marvin Minsky,人工智能与认知学专家)、克劳德·香农(Claude Shannon,信息论的创始人)、艾伦·纽厄尔(Allen Newell,计算机科学家)、赫伯特·西蒙(Herbert Simon,诺贝尔经济学奖得主) 等科学家正聚在一起,讨论着一个完全不食人间烟火的主题:
用机器来模仿人类学习以及其他方面的智能。
会议足足开了两个月的时间,虽然大家没有达成普遍的共识,但是却为会议讨论的内容起了一个名字:
人工智能
因此,1956年也就成为了人工智能元年。
- 1956年8月,在美国汉诺斯小镇宁静的达特茅斯学院中,约翰·麦卡锡(John McCarthy)、马文闵斯基(Marvin Minsky,人工智能与认知学专家)、克劳德·香农(Claude Shannon,信息论的创始人)、艾伦·纽厄尔(Allen Newell,计算机科学家)、赫伯特·西蒙(Herbert Simon,诺贝尔经济学奖得主) 等科学家正聚在一起,讨论着一个完全不食人间烟火的主题:
1.1.2 机器学习、深度学习能做些什么
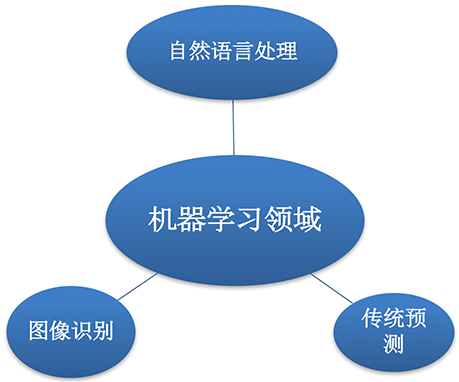
机器学习的应用场景非常多,可以说渗透到了各个行业领域当中。医疗、航空、教育、物流、电商等等领域的各种场景。
- 用在挖掘、预测领域:
- 应用场景:店铺销量预测、量化投资、广告推荐、企业客户分类、SQL语句安全检测分类…
- 用在图像领域:
- 应用场景:街道交通标志检测、人脸识别等等
- 应用场景:街道交通标志检测、人脸识别等等
- 用在自然语言处理领域:
- 应用场景:文本分类、情感分析、自动聊天、文本检测等等
- 应用场景:文本分类、情感分析、自动聊天、文本检测等等
当前重要的是掌握一些机器学习算法等技巧,从某个业务领域切入解决问题。
1.2 什么是机器学习
1.2.1 定义
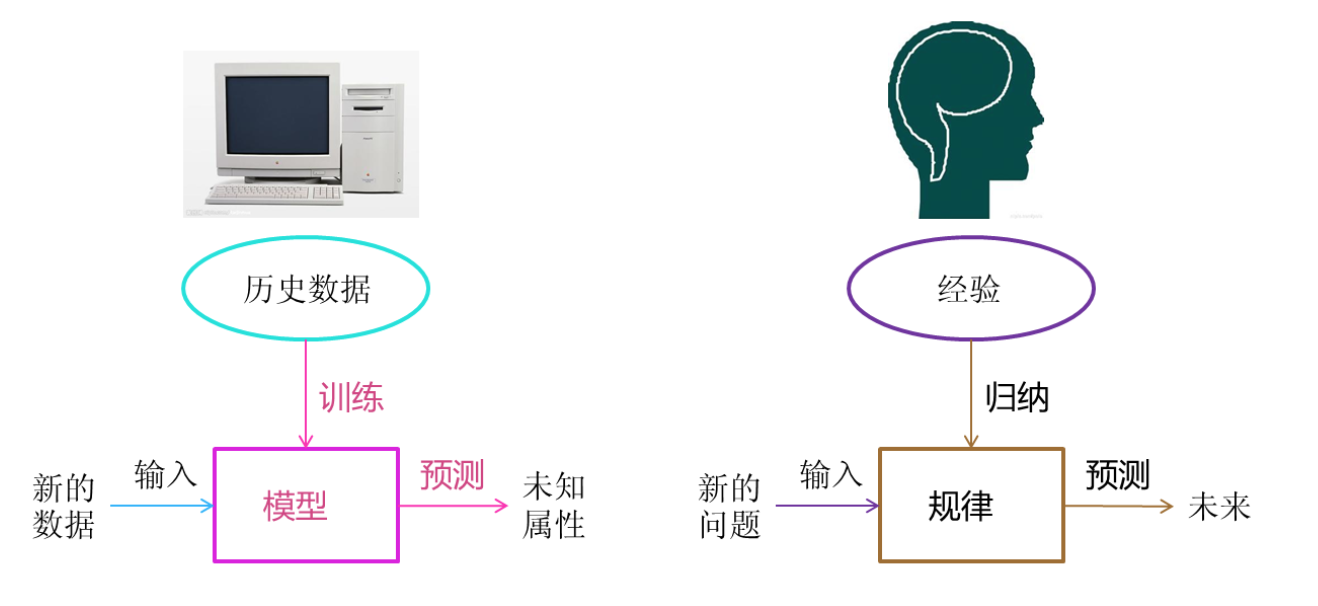
机器学习是从数据中自动分析获得模型,并利用模型对未知数据进行预测。
1.2.2 解释
-
我们人从大量的日常经验中归纳规律,当面临新的问题的时候,就可以利用以往总结的规律去分析现实状况,采取最佳策略。
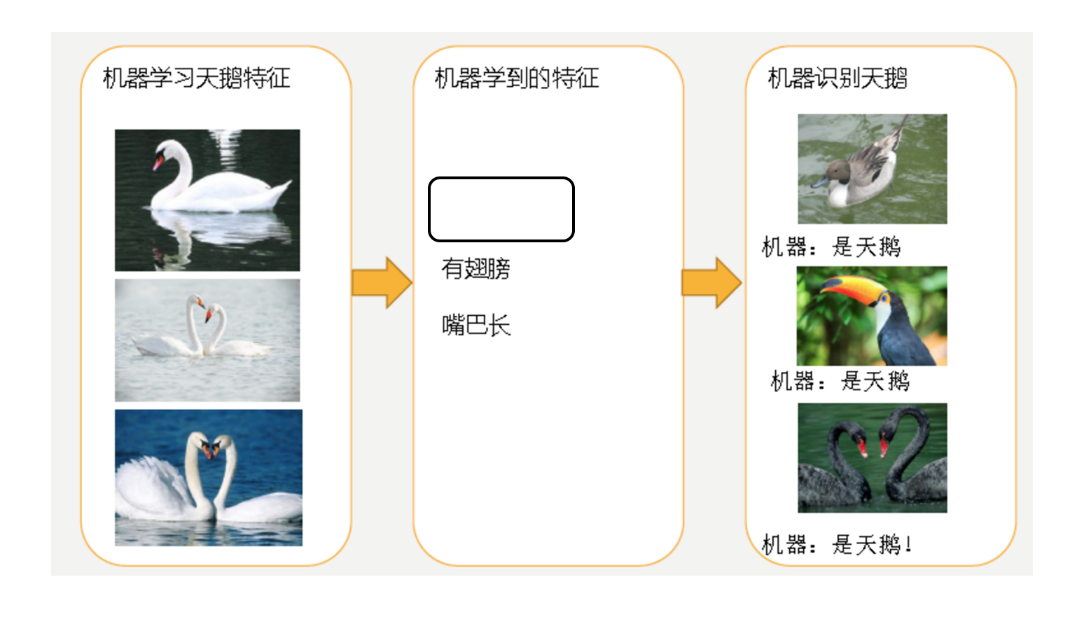
-
从数据(大量的猫和狗的图片)中自动分析获得模型(辨别猫和狗的规律),从而使机器拥有识别猫和狗的能力。
-
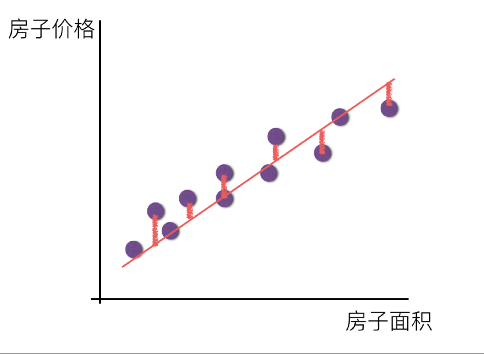
从数据(房屋的各种信息)中自动分析获得模型(判断房屋价格的规律),从而使机器拥有预测房屋价格的能力。
从历史数据当中获得规律?这些历史数据是怎么的格式?
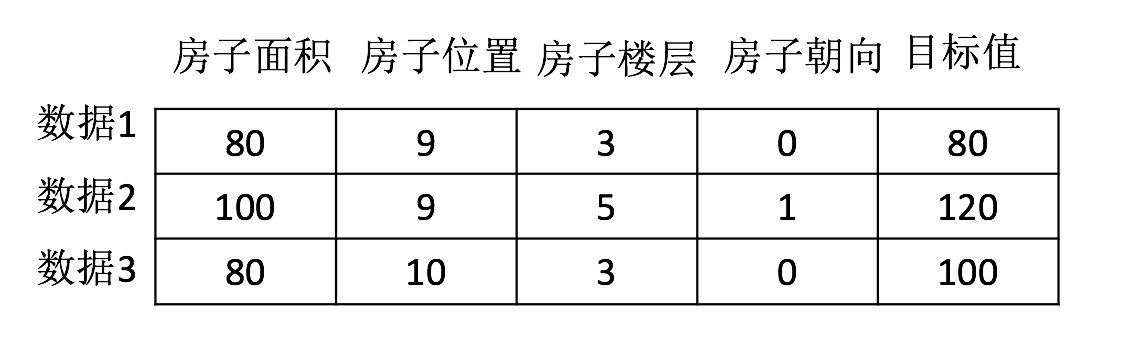
1.2.3 数据集构成
- 结构:
特征值 + 目标值
注:
- 对于每一行数据我们可以称之为样本。
- 有些数据集可以没有目标值:
1.3 机器学习算法分类
- 监督学习
- 目标值:类别 - 分类问题
- 目标值:连续型的数据 - 回归问题
- 无监督学习
- 目标值:无 - 无监督学习
分析1.2.2 中的例子:
- 特征值:猫/狗的图片;目标值:猫/狗-类别
- 分类问题
- 特征值:房屋的各个属性信息;目标值:房屋价格-连续型数据
- 回归问题
- 特征值:人物的各个属性信息;目标值:无
- 无监督学习
1.3.1 总结
1.3.2 练习
说一下它们具体问题类别:
1、预测明天的气温是多少度?
回归
2、预测明天是阴、晴还是雨?
分类
3、人脸年龄预测?
回归/分类, 看我们怎么定义这个年龄,比如说:
测心理年龄测试结果是26.1、50.1 … 这种就属于回归, 目标值是连续型的;
如果说测试心理年龄是 老的、小的 这种的话说明目标值是类别,这种就属于分类。
4、人脸识别?
分类虽然人脸识别最终的结果 他的目标值有很多很多,有多少个人就有不同的人脸,虽然类别很多但他还是分类
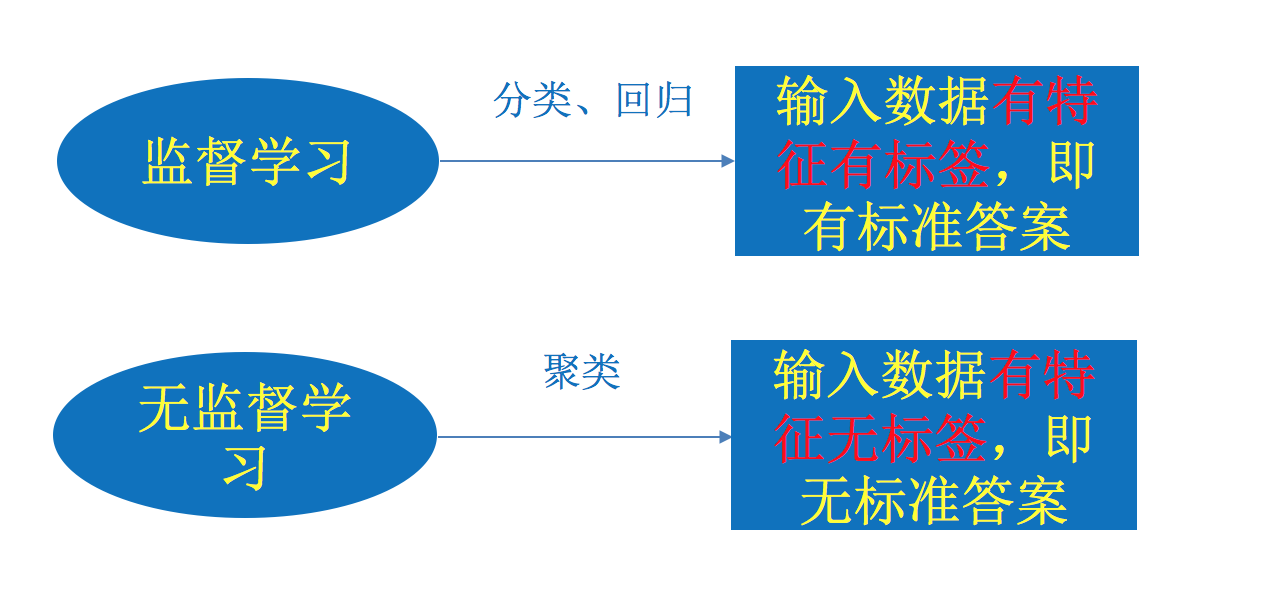
1.3.3 机器学习算法分类
- 监督学习(supervised learning)(预测)
- 定义:输入数据是由输入
特征值和目标值所组成。函数的输出可以是一个连续的值(称为回归),或是输出是有限个离散值(称作分类)。 - 分类算法 k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归、神经网络
- 回归算法 线性回归、岭回归
- 定义:输入数据是由输入
- 无监督学习(unsupervised learning)
- 定义:输入数据是由输入
特征值所组成。 - 聚类 k-means
- 定义:输入数据是由输入
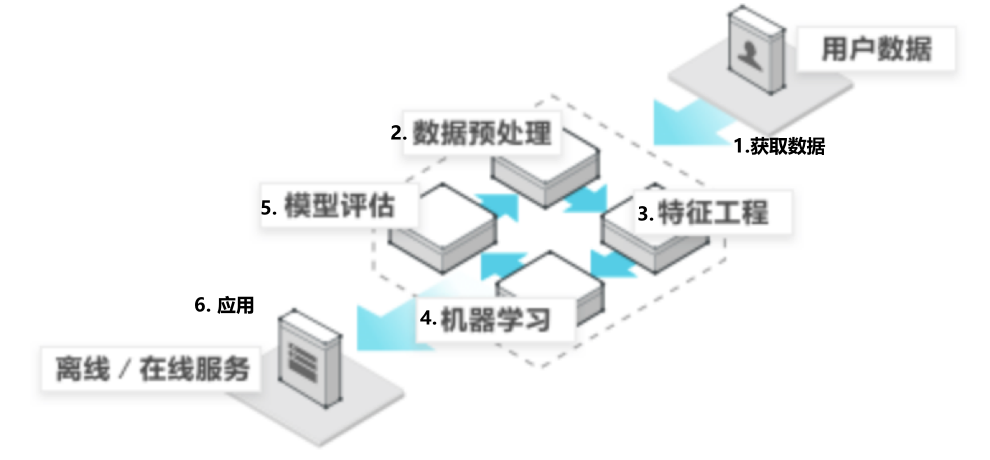
1.4 机器学习开发流程(了解)
1)获取数据
2)数据处理
比如:数据有缺失值处理一下缺失值;有一些数据不符合要求了给它处理掉。
3)特征工程
其实特征工程也算是在做数据处理,只不过我们将这些数据处理成更为直接能够被算法使用的数据。我们说机器学习的 数据集 分为 特征值 和 目标值,所以我们在处理数据的时候,直接叫特征工程,特征工程里的这个 特征 跟 特征值 是一回事。
4)机器学习算法训练 - 模型
选择合适的算法去训练了,训练好之后 得到一个模型。
5)模型评估
如果我们用一系列的方法看出这个模型效果比较好,那么就可以应用了;如果不好的话,还是要返回 数据处理 这一步,看看数据的处理有没有问题、看看特征工程做的好不好、看看算法选择有没有问题,这些都要检查一下,最终再看一下新的模型怎么样(模型评估),如果不好继续循环。直到模型评估比较好的,才可以应用。
6)应用
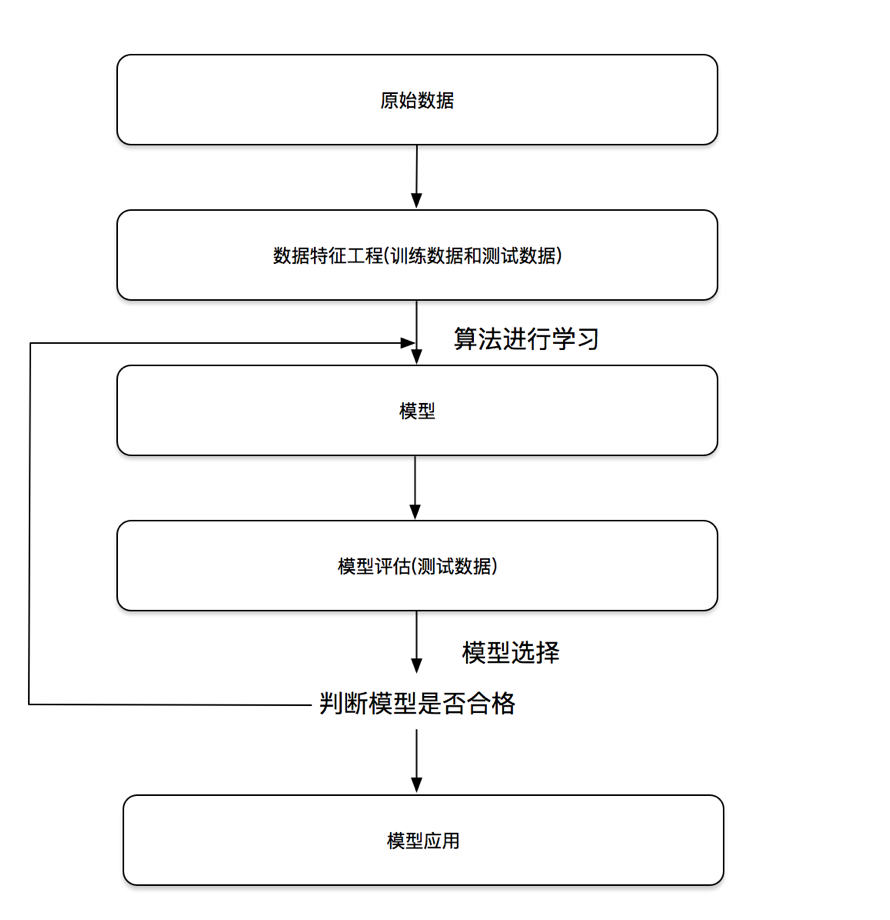
流程图:
1.5 学习框架和资料介绍
需明确几点问题:
(1)算法是核心,数据与计算是基础
(2)找准定位
大部分复杂模型的算法设计都是算法工程师在做,而我们
- 分析很多的数据
- 分析具体的业务
- 应用常见的算法
- 特征工程、调参数、优化
-
我们应该怎么做?
-
学会分析问题,使用机器学习算法的目的,想要算法完成何种任务
-
掌握算法基本思想,学会对问题用相应的算法解决
-
学会利用库或者框架解决问题
当前重要的是掌握一些机器学习算法等技巧,从某个业务领域切入解决问题。
1.5.1 机器学习库与框架
- 传统机器学习算法
- Scikit-lear
- 深度学习框架
- TensorFlow
- pytorch
- Caffe2
- theano(TensorFlow的前身)
- Chainer(pytorch的前身)
1.5.2 书籍资料
机器学习 -”西瓜书”- 周志华
统计学习方法 - 李航
深度学习 - “花书”
1.5.3 提深内功(但不是必须)
特征工程
了解特征工程在机器学习当中的重要性
应用sklearn实现特征预处理
应用sklearn实现特征抽取
应用sklearn实现特征选择
应用PCA实现特征的降维
2.1 数据集
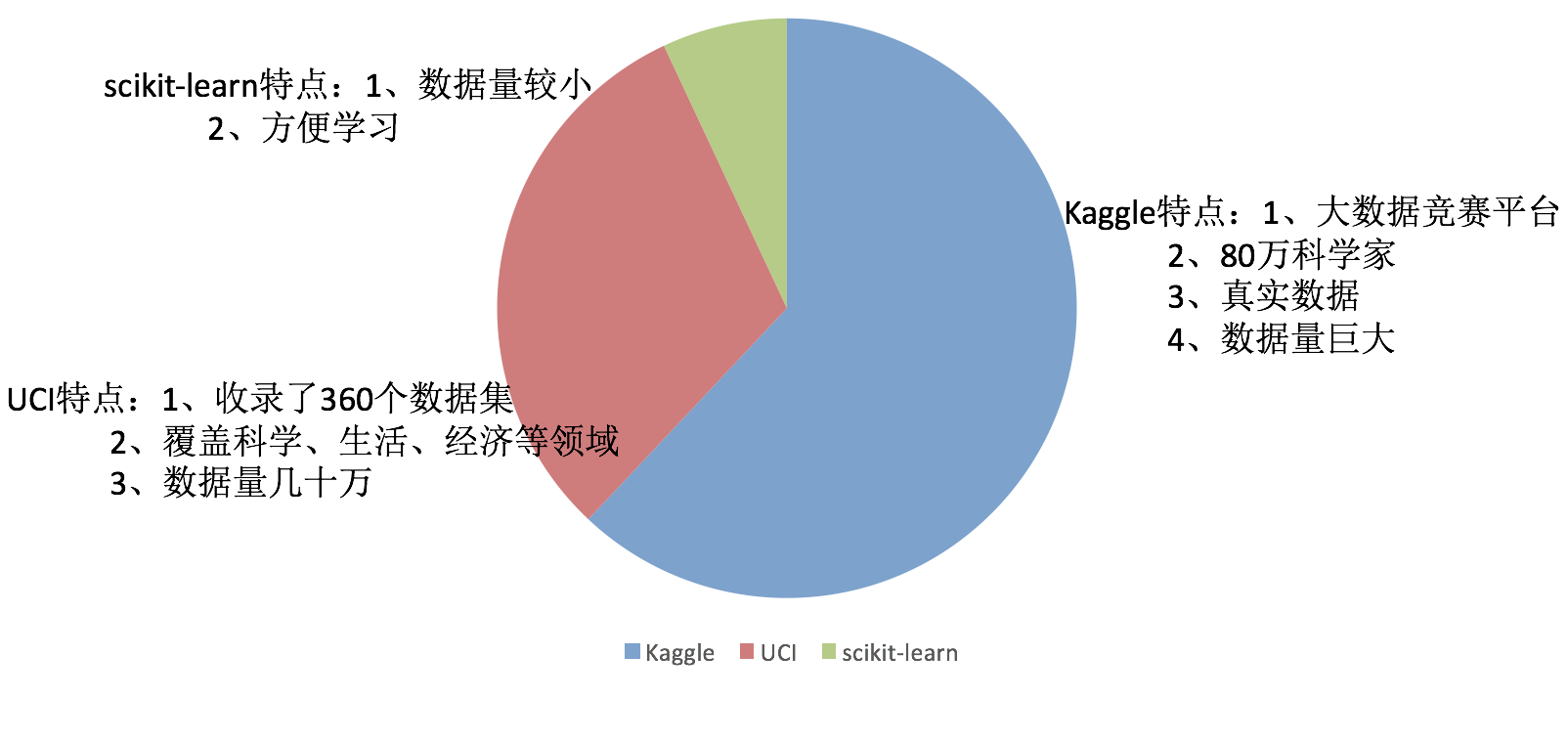
2.1.1 可用数据集
公司内部 百度
数据接口 花钱
Kaggle网址:https://www.kaggle.com/datasets
UCI数据集网址: http://archive.ics.uci.edu/ml/
scikit-learn网址:https://scikit-learn.org/stable/index.html
1、Scikit-learn工具介绍
- Python语言的机器学习工具
- Scikit-learn包括许多知名的机器学习算法的实现
- Scikit-learn文档完善,容易上手,丰富的API
- 本章用的版本 1.3.0
2、安装
pip install scikit-learn
可以指定版本号
pip3 install Scikit-learn==0.19.1
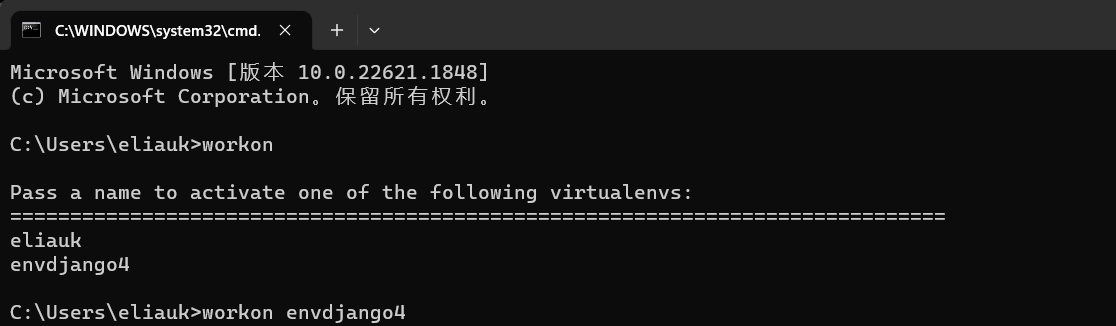
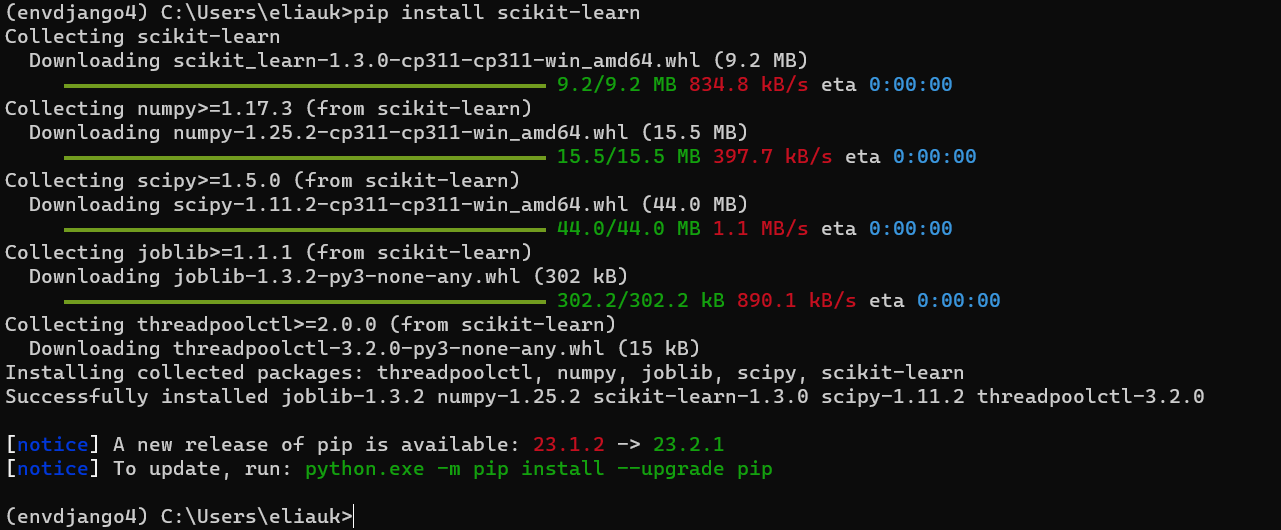
也可以在虚拟环境里安装
创建并进入虚拟环境eliauk
mkvirtualenv eliauk
安装win版本后可以是有命令进行虚拟环境的进入, 进入eliaukworkon eliauk
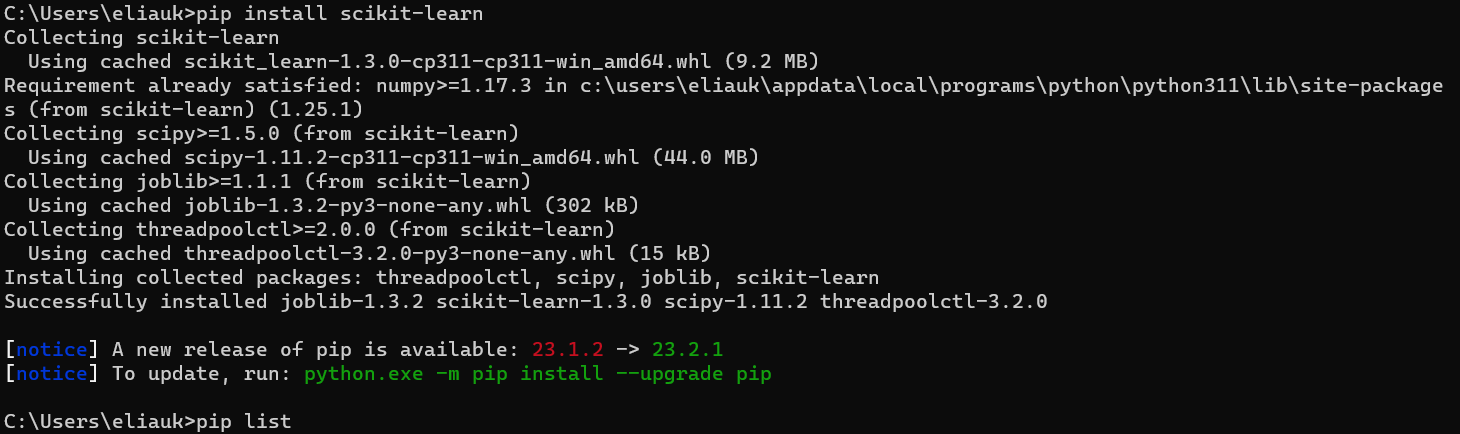
安装好之后可以通过以下命令查看是否安装成功
import sklearn
ipython是一个python的交互式shell
pip list看一下我们的环境
- 注:安装scikit-learn需要Numpy, Scipy等库
那你就把相应的库安装上就可以了。
3、Scikit-learn包含的内容
scikitlearn接口
- 分类、聚类、回归
- 特征工程
- 模型选择、调优
2.1.2 sklearn数据集
1、scikit-learn数据集API介绍
_* 是 _某一个数据集名字
- sklearn.datasets
- 加载获取流行数据集
- datasets.load_*()
- 获取小规模数据集,数据包含在- datasets里
- 返回Bunch类型
- datasets.fetch_*(data_home=None)
- 返回Bunch类型
- 获取大规模数据集,需要从网络上下载,函数的第一个参数是data_home,表示数据集下载的目录,默认是 ~/scikit_learn_data/
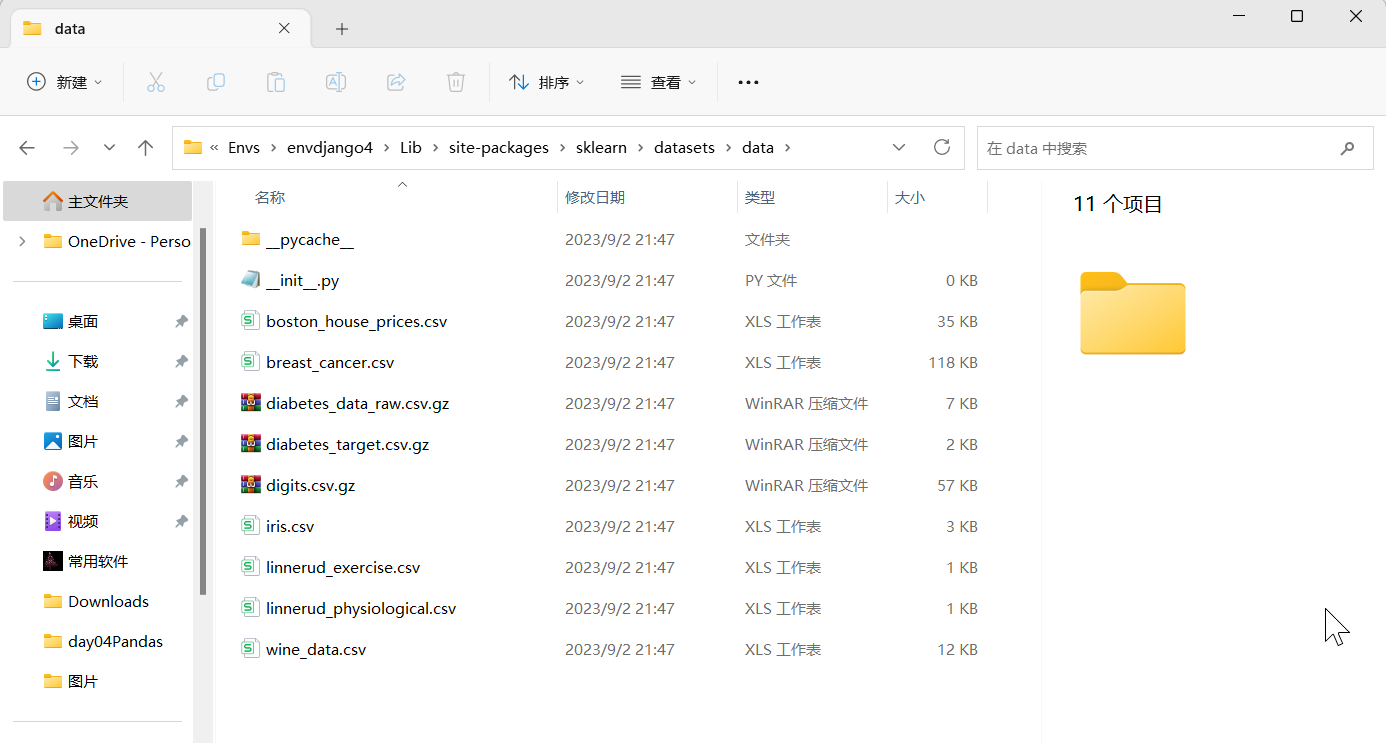
- 我的是windows,C:\Users\用户名\Envs\虚拟环境名\Lib\site-packages\sklearn\datasets\data
2、获取sklearn小数据集
- sklearn.datasets.load_iris()
加载并返回鸢尾花数据集
最受欢迎、用的比较多的数据集,鸢尾花数据集,是一个非常经典的数据集,在sklearn当中也有
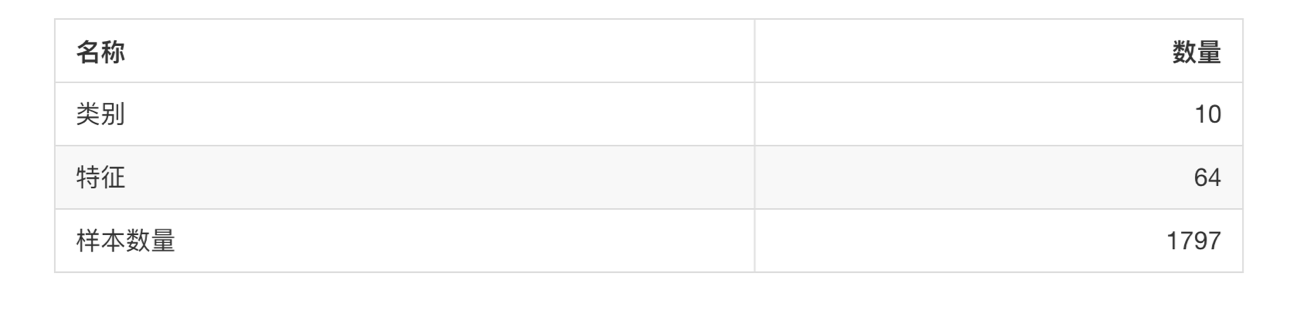
- sklearn.datasets.load_digits()
加载并返回数字数据集
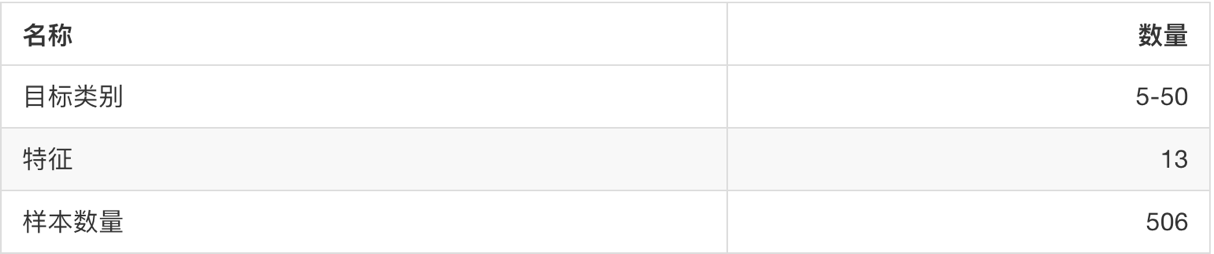
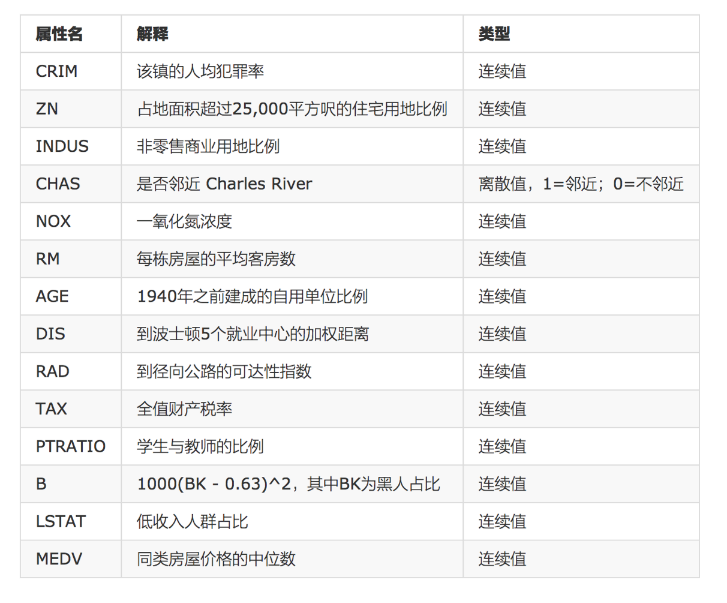
- sklearn.datasets.load_boston()
加载并返回波士顿房价数据集
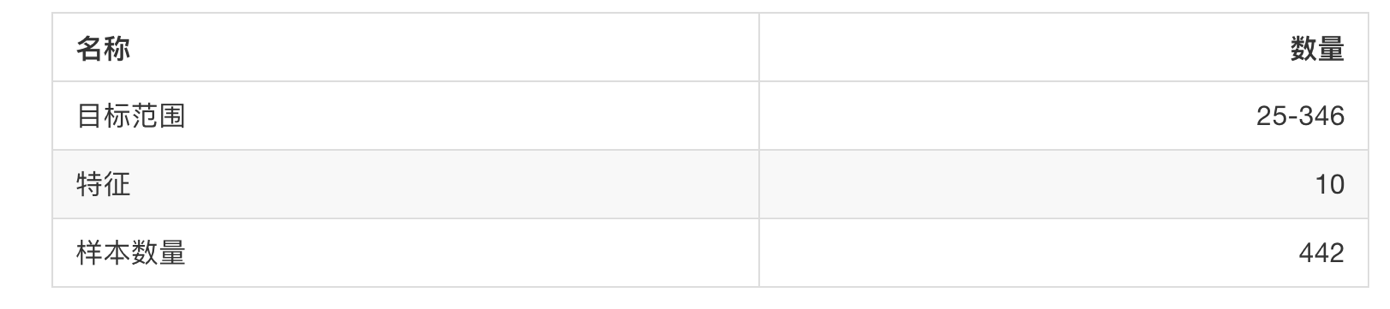
- sklearn.datasets.load_diabetes()
加载和返回糖尿病数据集
3、获取sklearn大数据集
- sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)
- subset:‘train’或者’test’,‘all’,可选,选择要加载的数据集。
- 训练集的“训练”train,测试集的“测试”test,两者的“全部” all
4、sklearn数据集的使用
- 以鸢尾花数据集为例:
sklearn数据集返回值介绍
- load 和 fetch 返回的数据类型datasets.base.
Bunch(字典格式),继承自字典- data:特征数据数组,是 [n_samples * n_features] 的二维 numpy.ndarray 数组
- target:标签数组,是 n_samples 的一维 numpy.ndarray 数组。目标值
- DESCR:数据描述
- feature_names:特征名,新闻数据,手写数字、回归数据集没有
- target_names:标签名。目标值的标签
- 字典的方式:
dict["key"] = values - .属性的方式:
bunch.key = values
from sklearn.datasets import load_iris
def datasets_demo():
"""
sklearn数据集使用
:return:
"""
# 获取数据集
iris = load_iris()
print("鸢尾花数据集:\n", iris)
return None
if __name__ == "__main__":
# 代码:sklearn数据集使用
datasets_demo()
结果:
鸢尾花数据集:
{'data': array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
...,
[5.9, 3. , 5.1, 1.8]]),
'target': array([0, 0, 0, 0, ..., 0, 1, 1, ..., 1, 1, 2,..., 2, 2]),
'frame': None,
'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),
'DESCR': '.. _iris_dataset:\n\nIris plants dataset...',
'feature_names': ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'],
'filename': 'iris.csv', 'data_module': 'sklearn.datasets.data'}
data 特征数据数组(特征值),是一个二维数组,它的类型是ndarray,Numpy是很多库的基础库,所以sklearn也是有Numpy的。
target 目标值(标签值),也是一个数组ndarray,目标值。target_names目标值的标签。0对应一类setosa, 1代表另一类versicolor。
DESCR 描述,不是特别清楚。
思考:拿到的数据是否全部都用来训练一个模型?
否
2.1.3 数据集的划分
机器学习一般的数据集会划分为两个部分:
- 训练数据:用于训练,构建模型
- 测试数据:在模型检验时使用,用于评估模型是否有效
划分比例:
- 训练集:70% 80% 75%
- 测试集:30% 20% 30%
数据集划分api
- sklearn.model_selection.train_test_split(arrays, *options)
- x 数据集的特征值
- y 数据集的标签值(目标值)
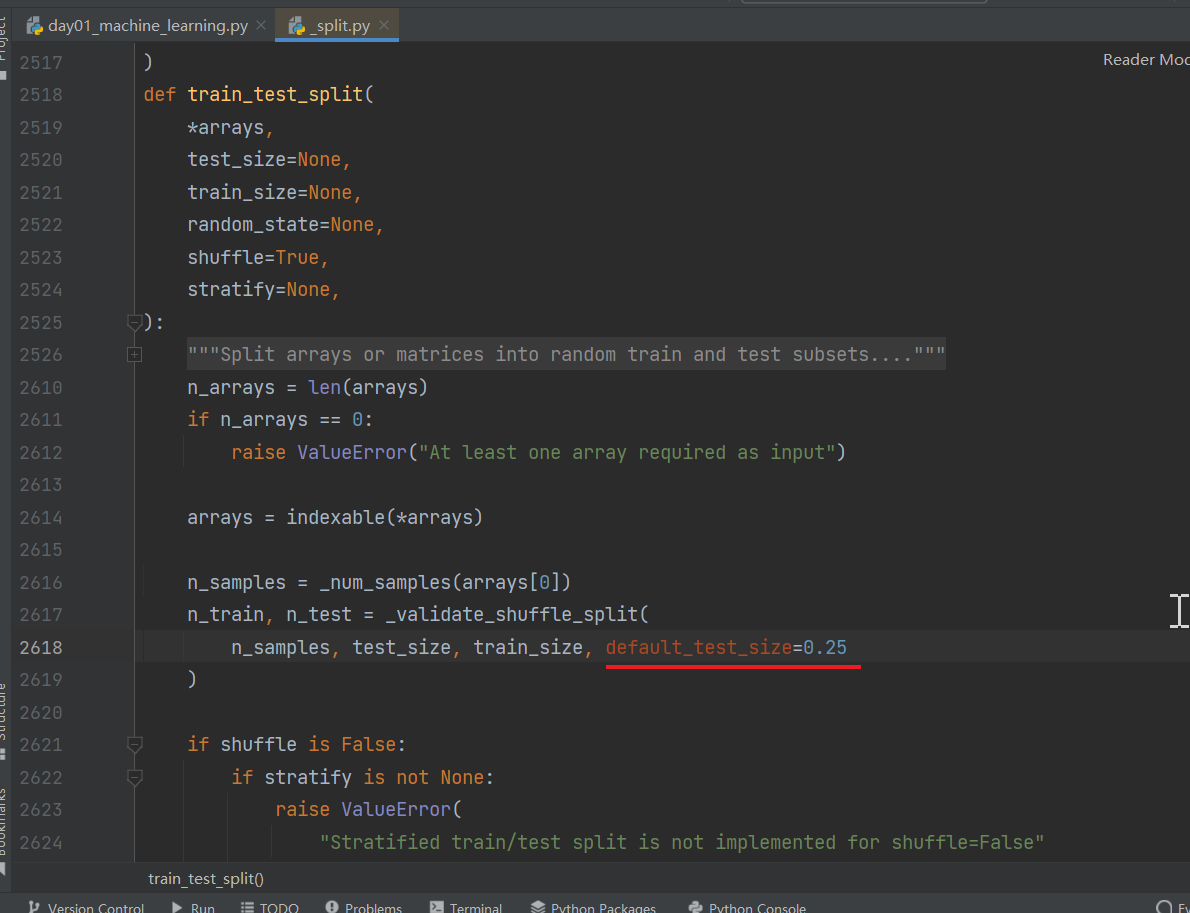
- test_size 测试集的大小,一般为float,比如想要设置20%那么就传入0.2。不传默认0.25
- random_state 随机数种子(大家都知道计算机伪随机),不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
- 返回值 :return 训练集特征值,测试集特征值,训练集目标值,测试集目标值
取名x_train, x_test, y_train, y_test
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def datasets_demo():
"""
sklearn数据集使用
:return:
"""
# 获取数据集
iris = load_iris()
print("鸢尾花数据集:\n", iris)
# 返回值是一个继承自字典的Bench
print("查看数据集的描述:\n", iris.DESCR) # iris['DESCR']
print("鸢尾花的特征值:\n", iris["data"],iris["data"].shape)# (150, 4)
print("鸢尾花特征的名字:\n", iris.feature_names) # ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
print("鸢尾花的目标值:\n", iris.target,iris.target.shape)
"""
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2] (150,)
"""
print("鸢尾花目标值的名字:\n", iris.target_names)
# 数据集划分
# 训练集的特征值x_train 测试集的特征值x_test 训练集的目标值y_train 测试集的目标值y_test
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
print("x_train:\n", x_train, x_train.shape)# (120, 4)
print("x_test:\n", x_test, x_test.shape)# (30, 4)
print("y_train:\n", y_train, y_train.shape)# (120,)
print("y_test:\n", y_test, y_test.shape)# (30,)
# 随机数种子
x_train1, x_test1, y_train1, y_test1 = train_test_split(iris.data, iris.target, test_size=0.2, random_state=6)
x_train2, x_test2, y_train2, y_test2 = train_test_split(iris.data, iris.target, test_size=0.2, random_state=6)
print("如果随机数种子不一致:\n", x_train == x_train1)
print("如果随机数种子一致:\n", x_train1 == x_train2)
return None
if __name__ == "__main__":
# 代码:sklearn数据集使用
datasets_demo()
2.2 特征工程介绍
这个图是一个数据科学的网站,里面有很多关于数据科学的比赛,这是有一个比赛的结果,可以看到这里有参赛者、组织、分数。我们可以看到,面对同样的问题就有不同的分数,这些分数其实是比较接近的。
为什么面对同样的问题他们的分数(最终效果、结果)会不一样?
影响最终效果可能的原因就是:
1.使用的算法
2.数据处理的怎么样,也就是特征工程
其实这些人用的工具不是TensorFlow就是什么什么pytorch又或者sklearn等等,能用的工具其实差不多,经典算法大家知道的也是差不多的。能排名靠这么前的,肯定知道的算法也都差不多。所以说根据这个算法,他们很可能用的是同一种算法。为什么结果会有差距呢?
其实就是在于特征工程是千变万化的,可能做特征工程、数据处理部分是不一样的,导致最终的效果差别。
2.2.1 为什么需要特征工程(Feature Engineering)
机器学习领域的大神Andrew Ng(吴恩达)老师说“Coming up with features is difficult, time-consuming, requires expert knowledge. “Applied machine learning” is basically feature engineering. ”
注:业界广泛流传:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
2.2.2 什么是特征工程
特征工程是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用的过程。
- 意义:会直接影响机器学习的效果
2.2.3 特征工程的位置与数据处理的比较
- pandas:一个数据读取非常方便以及基本的处理格式的工具
- 一般做数据清洗、数据处理
- sklearn:对于特征的处理提供了强大的接口
特征工程包含内容
- 特征抽取(或者特征提取)
- 特征预处理
- 特征降维
2.3 特征提取(特征抽取)
学习目标
- 目标
- 应用DictVectorizer实现对类别特征进行数值化、离散化
- 应用CountVectorizer实现对文本特征进行数值化
- 应用TfidfVectorizer实现对文本特征进行数值化
- 说出两种文本特征提取的方式区别
其实是相当于是将字典当中的类别给转换成one-hot编码。
文本特征抽取(介绍了两种方法)
CountVectorizer 去统计每一个文档它当中的这些特征词出现的个数
TfidfVectorizer 计算Tf-idf 这样的一个指标去找到这篇文章这些词的重要性程度,其实是更有利于我们进一步的分类的。
什么是特征提取呢?
第一个例子: 这是一篇英文的短文,我们如果想要对这篇短文做一些处理,比如做文章的分类,分成不同的类别,想要用机器学习算法去做,会出现什么问题?
左边英文短文相当于 数据集,数据集想要用机器学习算法去做,那么什么是机器学习算法呢?
机器学习其实就是当时搞统计的那些人想出来的 去实现人工智能的一个途径,机器学习算法 其实就是一些 统计方法 ,统计方法 又是一个又一个 数学公式。数学公式它能够处理字符串吗?数学公式肯定不能处理字符串,但是我们这个数据就是字符串,我们需要将文本类型的 这个存成的字符串 给它转换成 右边数值的类型 。但是怎么转换比较合适呢?转换成什么样子才能达到我们最终的目的呢?这就是我们特征提取、特征抽取 要考虑的事情。
机器学习算法 - 统计方法 - 数学公式
文本类型 => 数值
类型 => 数值
第二个例子: 我有一组数据,想要对数据进行分类,那么我们数据当中有这些特征 pclass(泰坦尼克号数据集里的特征,pclass代表所乘的舱位,一等舱、二等舱)、sex ,我们发现存成什么了?是不是还是字符串呀,它们都表示的是类别。
我们在前面 数据挖掘基础阶段,当我们想要处理一些数据,这些数据当中有一些数据当中是类别的话,类别我们通常存储成字符串,但我们现在要用机器学习算法去处理这些数据,是不是还是要将类型转换成数值,怎么转?这个当时有讲方法,转换成one-hot编码 或者 哑变量
为什么要进行特征提取?我们一些数据一开始不能直接被机器学习算法处理,需要用一种方式来把它进行这样的转换,至于怎么转换呢,不同的类型的数据有不同的转换方法。
2.3.1 特征提取
1、将任意数据(如文本或图像)转换为可用于机器学习的数字特征
注:特征值化是为了计算机更好的去理解数据
- 字典特征提取(特征离散化)
- 文本特征提取
- 图像特征提取(深度学习将介绍)
2、特征提取API
在sklearn有一个feature_extraction类
sklearn.feature_extraction
2.3.2 字典特征提取 DictVectorizer
作用:对字典数据进行特征值化
sklearn.feature_extraction.DictVectorizer(sparse=True,…)- Vector 向量、矢量
矩阵 matrix 二维数组,从线性代数当中,矩阵可以从另一个角度看它,可以看成它是由向量构成的,可以横着看可以竖着看,都可以看成是由向量构成的。
如果将向量存储在计算机当中,那就是一维数组。
向量 vector 一维数组
DictVectorizer 字典进行向量化,其实就是告诉计算机我要把字典转换成数值。 - sparse 稀疏
- 参数值
- =True 默认参数会返回一个稀疏矩阵(返回sparse矩阵对象 scipy.sparse._csr.csr_matrix )
- 将非零值 按位置表示出来
- 节省内存 - 提高加载效率
- sparse矩阵对象.toarray() 返回一个二维数组【跟DictVectorizer(sparse=False).fit_transform(X) 一样的结果】
- =False 会返回一个one-hot编码矩阵
- =True 默认参数会返回一个稀疏矩阵(返回sparse矩阵对象 scipy.sparse._csr.csr_matrix )
- 参数值
DictVectorizer.fit_transform(X)X:字典或者包含字典的迭代器返回值:返回sparse矩阵DictVectorizer.inverse_transform(X)X:array数组或者sparse矩阵 返回值:转换之前数据格式- DictVectorizer.get_feature_names() 返回类别名称
如果报错:AttributeError: ‘DictVectorizer’ object has no attribute ‘get_feature_names’. Did you mean: ‘get_feature_names_out’?
原因:函数get_feature_names在1.0中已弃用,在1.2中删除。改用DictVectorizer.get_feature_names_out()。 我的版本是 1.3.0
- Vector 向量、矢量
我们调用sklearn.feature_extraction.DictVectorizer()之后相当于实例化了一个 转换器对象 ,它的父类叫TransformerMixin 转换器类,其中一个方法就是把字典转换成数值。
1、应用
我们对以下数据进行特征提取
[{'city': '北京','temperature':100}
{'city': '上海','temperature':60}
{'city': '深圳','temperature':30}]
实际上我们发现它是按样本,每一个样本 {‘city’: ‘北京’,‘temperature’:100} 转换成了一个向量,n个样本就是n个向量,就成了一个二维数组,我们可以理解成二维数组,也可以理解成矩阵。
字典特征提取 - 类别 -> one-hot编码
2、流程分析
- 实例化类DictVectorizer
- 调用fit_transform方法输入数据并转换(注意返回格式)
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
"""
对字典类型的数据进行特征抽取
:return: None
"""
data = [{'city': '北京', 'temperature': 100}, {'city': '上海', 'temperature': 60}, {'city': '深圳', 'temperature': 30}]
# 1、实例化一个转换器类
# transfer = DictVectorizer() # 使用默认参数会返回一个稀疏矩阵
transfer = DictVectorizer(sparse=False) # 会返回一个one-hot编码矩阵
# 2、调用fit_transform
data_new = transfer.fit_transform(data)
print("type(data_new):\n", type(data_new))
# 没加参数sparse=False -> <class 'scipy.sparse._csr.csr_matrix'>
# 加了参数sparse=False -> <class 'numpy.ndarray'>
print("返回的结果:\n", data_new)
# 打印特征名字
# print("特征名字:\n", transfer.get_feature_names())
# 报错:AttributeError: 'DictVectorizer' object has no attribute 'get_feature_names'. Did you mean: 'get_feature_names_out'?
# 原因: 函数get_feature_names已弃用;get_feature_names在1.0中已弃用,将在1.2中删除。请改用。
# 我的版本是 1.3.0
print("特征名字:\n", transfer.get_feature_names_out())
return None
if __name__ == "__main__":
dict_demo()
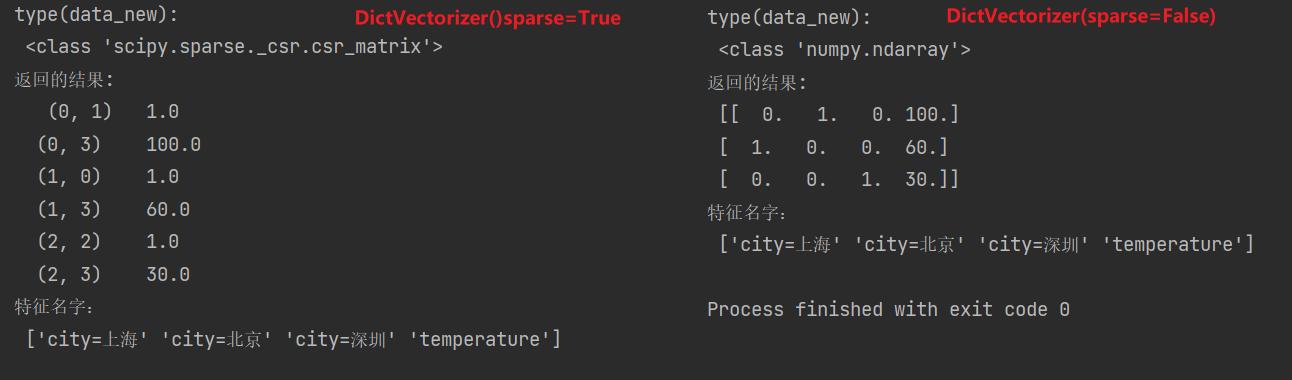
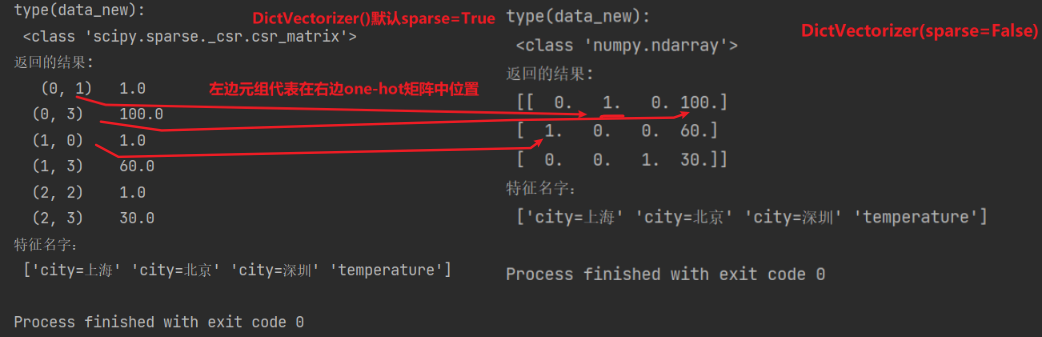
注意观察没有加上sparse=False参数(默认True)的结果
type(data_new):
<class 'scipy.sparse._csr.csr_matrix'>
返回的结果:
(0, 1) 1.0
(0, 3) 100.0
(1, 0) 1.0
(1, 3) 60.0
(2, 2) 1.0
(2, 3) 30.0
特征名字:
['city=上海' 'city=北京' 'city=深圳' 'temperature']
这个结果并不是我们想要看到的,所以加上参数sparse=False,得到想要的结果:
type(data_new):
<class 'numpy.ndarray'>
返回的结果:
[[ 0. 1. 0. 100.]
[ 1. 0. 0. 60.]
[ 0. 0. 1. 30.]]
特征名字:
['city=上海' 'city=北京' 'city=深圳' 'temperature']
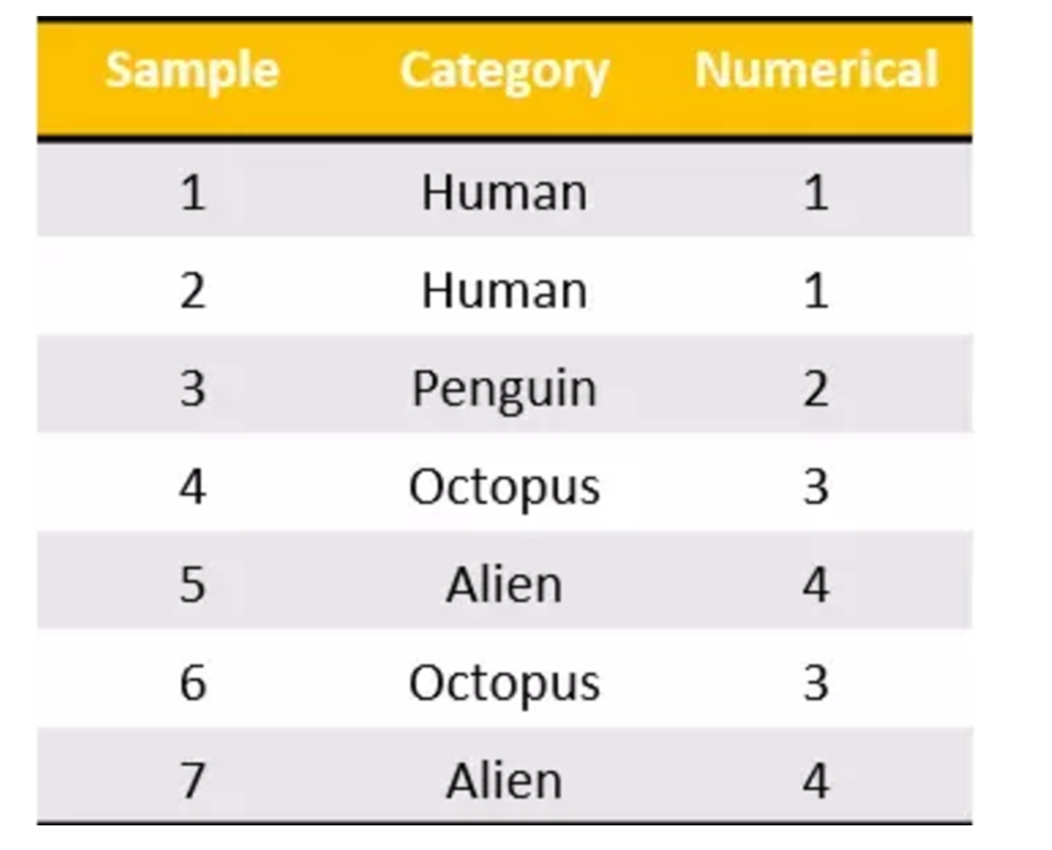
之前在学习pandas中的离散化的时候,也实现了类似的效果。
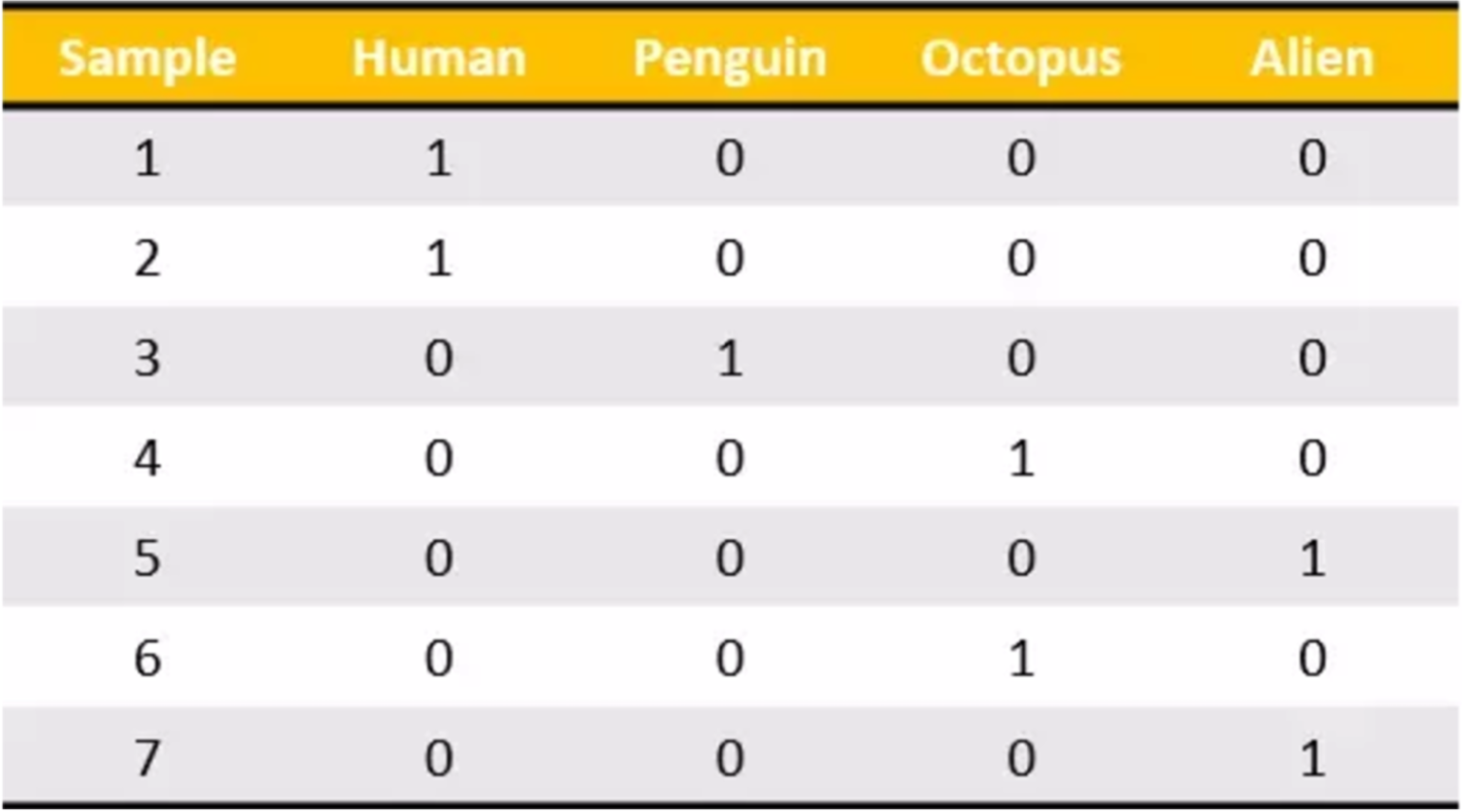
我们把这个处理数据的技巧叫做”one-hot“编码:
转化为:
我们做的是为每个类别生成一个布尔列。这些列中只有一列可以为每个样本取值1。因此,术语一个热编码。
3、对比两个结果理解一下稀疏矩阵和one-hot编码
sparse稀疏矩阵将非0值按照位置表示出来,这样做有什么好处呢?右边的是将类别转换成为one-hot编码,如果类别特别多呢?假设有一千个的时候,这样会使得0特别多,这时候用左边的稀疏矩阵可以提高加载效率,节省内存。
注意:使用one-hot编码是为了让类别更加公平一点,相互之间没有优先级,在特征中对类别信息常用ont-hot编码处理
字典特征抽取-应用场景:
(1)数据集当中类别特征比较多 , 例如pclass, sex 都是类别特征
1、将数据集的特征 -> 字典类型
2、DictVectorizer转换
(2)本身拿到的数据就是字典类型
就用字典特征抽取
总结
对于特征当中存在类别信息的我们都会做one-hot编码处理
2.3.3 文本特征提取
作用:对文本数据进行特征值化
单词 作为 特征
句子、短语、单词、字母
特征:特征词(单词)
如果把一篇文章进行分类的话,我们把什么作为它的特征能更容易的进行分类?如果没有标题的话,就把单词作为特征是比较合适的,其实一篇文章要去划分的话可以有很多要素,我们也可以以 句子 作为一个单位,也可以以 短语(短句子),除了单词之外还可以以字母。这些那些作为特征更合适呢?单词最为合适。为什么不用句子呢?其实用句子也不是不可以,但是不太现实,因为一个句子是由多个单词构成的,如果用句子作为特征的话,排列组合起来特征太多了,那就不太好处理了,所以一般我们用单词作为特征。
方法 1:CountVectorizer
sklearn.feature_extraction.text.CountVectorizer(stop_words=[])- stop_words停用的
我们认为有一些词也是不具备 对最终分类有好处的,比如 “is”、“too” 这种比较虚一点的词,以列表的形式传给CountVectorizer,这些词从哪来?感兴趣的话可以搜索 停用词表 ,这里就不扩展了 - 返回词频矩阵(返回sparse矩阵对象 scipy.sparse._csr.csr_matrix )
- 内部的方法
sparse矩阵对象.toarray()返回一个二维数组
- 内部的方法
- stop_words停用的
- CountVectorizer.fit_transform(X) X:文本或者包含文本字符串的可迭代对象 返回值:返回sparse矩阵
- CountVectorizer.inverse_transform(X) X:array数组或者sparse矩阵 返回值:转换之前数据格
- CountVectorizer.get_feature_names() 返回值:单词列表
sklearn.feature_extraction.text.TfidfVectorizer
1、应用
我们对以下数据进行特征提取
["life is short,i like python",
"life is too long,i dislike python"]
它会将文章中的单词作为特征词,但是我们发现 ’ i ’ 没有放进来。 为什么不把 ’ i ’ 作为特征词呢?因为我们认为这个 ’ i ’ 是单词的话要想进行分类(或者情感分析)它的意义不大,所以API在设计的时候自动的把标点符号、字母 就直接不统计 不作为最终的特征词列表。
0、1是对单词的一个计数
2、流程分析
- 实例化类CountVectorizer
- 调用fit_transform方法输入数据并转换 (注意返回格式,利用toarray()进行sparse矩阵转换array数组)
from sklearn.feature_extraction.text import CountVectorizer
def text_count_demo():
"""
对文本进行特征提取,countvetorizer
:return:None
"""
data = ["python life is short,i like python", "life is too long,i dislike python"]
# 1、实例化一个转换器类
transfer = CountVectorizer()
# transfer = CountVectorizer(sparse=False) # 报错: 不存在sparse这样一个参数。TypeError: CountVectorizer.__init__() got an unexpected keyword argument 'sparse'
# 2、调用fit_transform
data_new = transfer.fit_transform(data)
print('data_new:\n', data_new) # sparse矩阵
print('type(data_new): ', type(data_new)) # <class 'scipy.sparse._csr.csr_matrix'>
print('data_new.toarray:\n', data_new.toarray())
# print("返回特征名字:\n", transfer.get_feature_names())
print("返回特征名字:\n", transfer.get_feature_names_out())
return None
if __name__ == "__main__":
text_count_demo()
返回结果:
data_new:
(0, 5) 2
(0, 2) 1
(0, 1) 1
(0, 6) 1
(0, 3) 1
(1, 5) 1
(1, 2) 1
(1, 1) 1
(1, 7) 1
(1, 4) 1
(1, 0) 1
type(data_new): <class 'scipy.sparse._csr.csr_matrix'>
data_new.toarray:
[[0 1 1 1 0 2 1 0]
[1 1 1 0 1 1 0 1]]
返回特征名字:
['dislike' 'is' 'life' 'like' 'long' 'python' 'short' 'too']
问题:如果我们将数据替换成中文?
中文文本特征抽取
from sklearn.feature_extraction.text import CountVectorizer
def text_count_chinese_demo():
"""
对中文文本进行特征提取,countvetorizer
:return:None
"""
data = ["我爱派森", "派森你好呀"]
# 1、实例化一个转换器类
transfer = CountVectorizer()
# 2、调用fit_transform
data_new = transfer.fit_transform(data)
# print('data_new:\n', data_new)
# print('type(data_new): ', type(data_new))
print('文本特征抽取的结果:\n', data_new.toarray())
# print("返回特征名字:\n", transfer.get_feature_names())
print("返回特征名字:\n", transfer.get_feature_names_out())
return None
if __name__ == "__main__":
text_count_chinese_demo()
结果:
文本特征抽取的结果:
[[1 0]
[0 1]]
返回特征名字:
['我爱派森' '派森你好呀']
我们发现这并不是我们想要的结果,它把 短语 作为 特征 了。这样是不合适的,我们需要把单词作为特征。
为什么会这样的情况?仔细分析之后会发现英文默认是以空格分开的。其实就达到了一个分词的效果,所以我们要对中文进行分词处理。
因为英文本身是有空格去隔开一个又一个的词,中文有那个语言的特写,它就不会有这样一个分隔,所以最终认为这整个是一个词,然后进行这样的一个划分。
如果想要达到比较好的一个效果(正常的效果),我们应该怎么办?把中文隔开进行分词。
data = ["我 爱 派森", "派森 你好 呀"]
结果:
文本特征抽取的结果:
[[0 1]
[1 1]]
返回特征名字:
['你好' '派森']
刚刚我们是手动分词,现在我们可以借助一些工具来自动的进行分词,比如jieba分词(Python 中文分词库)
CountVectorizer(stop_words=) 体验
from sklearn.feature_extraction.text import CountVectorizer
def text_count_demo():
"""
对文本进行特征提取,countvetorizer
:return:None
"""
data = ["python life is short,i like python", "life is too long,i dislike python"]
# 1、实例化一个转换器类
transfer = CountVectorizer(stop_words=["is", "too"])
# 2、调用fit_transform
data_new = transfer.fit_transform(data)
print('文本特征抽取的结果:\n', data_new.toarray())
# print("返回特征名字:\n", transfer.get_feature_names())
print("返回特征名字:\n", transfer.get_feature_names_out())
return None
if __name__ == "__main__":
text_count_demo()
结果:
文本特征抽取的结果:
[[0 1 1 0 2 1]
[1 1 0 1 1 0]]
返回特征名字:
['dislike' 'life' 'like' 'long' 'python' 'short']
3、jieba分词处理
- jieba.cut()
- 返回词语组成的生成器
需要安装下jieba库
pip3 install jieba
4、案例
对以下三句话进行特征值化
沉溺在“如果情况不同又会发生什么”的设想里,
绝对是让人精神失常的不二法门。
我们看到的从很远星系来的光是在几百万年之前发出的,
这样当我们看到宇宙时,我们是在看它的过去。
如果只用一种方式了解某样事物,你就不会真正了解它。
了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。
- 分析
- 准备句子,利用jieba.cut进行分词
- 实例化CountVectorizer
- 将分词结果变成字符串当作fit_transform的输入值
from sklearn.feature_extraction.text import CountVectorizer
import jieba
def cut_words(text):
"""
进行中文分词
"我爱北京天安门"————>"我 爱 北京 天安门"
:param text:
:return:text
"""
# print(jieba.cut(text)) # 返回一个词语生成器 <generator object Tokenizer.cut at 0x000002736CC1A140>
# a = list(jieba.cut(text))# ['我', '爱', '北京', '天安门']
# a = " ".join(list(jieba.cut(text)))# "我 爱 北京 天安门"
# a = " ".join(jieba.cut(text)) # 这里直接join生成器也可以, 一样的效果 # "我 爱 北京 天安门"
# print(a)
return " ".join(jieba.cut(text))
def text_count_chinese_demo02():
"""
中文文本特征提取, 自动分词
:return:None
"""
data = ["一种还是一种沉溺在“如果情况不同又会发生什么”的设想里,绝对是让人精神失常的不二法门。",
"我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。",
"如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
new_data = []
# 1.将中文文本进行分词
for sent in data:
new_data.append(cut_words(sent))
print(new_data)
# 2、实例化一个转换器类
transfer = CountVectorizer()
# transfer = CountVectorizer(stop_words=["一种", "所以"]) # 指定的词语去掉,不作为特征
# 3、调用fit_transform
data_final = transfer.fit_transform(new_data)
print('文本特征抽取的结果:\n', data_final.toarray())
# print("返回特征名字:\n", transfer.get_feature_names())
print("返回特征名字:\n", transfer.get_feature_names_out())
return None
if __name__ == "__main__":
# print(cut_words("我爱北京天安门")) # 中文分词
text_count_chinese_demo02()
返回结果:
Building prefix dict from the default dictionary ...
Loading model from cache C:\Users\eliauk\AppData\Local\Temp\jieba.cache
Loading model cost 0.712 seconds.
Prefix dict has been built successfully.
['一种 还是 一种 沉溺在 “ 如果 情况 不同 又 会 发生 什么 ” 的 设想 里 , 绝对 是 让 人 精神失常 的 不二法门 。', '我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 , 这样 当 我们 看到 宇宙 时 , 我们 是 在 看 它 的 过去 。', '如果 只用 一种 方式 了解 某样 事物 , 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。']
文本特征抽取的结果:
[[2 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0]
[0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 1 0 3 0 1 0 0 2 0 0 0 0 0 0 1 0 1]
[1 0 1 0 0 4 3 0 0 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 2 1 0 0 1 0 0 0 0]]
返回特征名字:
['一种' '不二法门' '不会' '不同' '之前' '了解' '事物' '什么' '光是在' '几百万年' '发出' '发生' '取决于'
'只用' '含义' '如何' '如果' '宇宙' '情况' '我们' '方式' '星系' '某样' '沉溺在' '看到' '真正' '秘密'
'精神失常' '绝对' '联系' '设想' '过去' '还是' '这样']
但如果把这样的词语特征用于分类,会出现什么问题?
思考
思考一个问题,我们用CountVectorizer的方式进行对文本特征的抽取 是这样的一个结果,这样的结果有什么问题?对于最终想要实现 文本分类 这样一个目的来说 ,这么分词,这么特征提取 有没有什么不好的地方?
我们看到,在这个二维数组里面,相当于有三个样本,有很多个特征,我们如果进行文本分类的话,那么就是根据特征进行分类。怎样的特征呢?我们认为数值上比较大的,我们认为对最终的结果影响会更大一点。
在第三个样本中,“了解” 这个词在第三个样本中占了4次,“事物” 出现了三次 ,如果用这样的数据进行分类的话,“了解”、“事物” 这两个词可能会对最终结果产生更大的影响。那么这样我们相当于只是根据一个词在这篇文章中出现的次数来进行分类的,出现的次数越多可能就认为更属于这个类别。
但现在就有一个问题了,比如像"我们"、“你们”、“他们”、“只有”、“因为”、“所以”…这些词不仅在你这篇文章,在其他文章当中也可能经常出现,像这样的词,如果我们把它统计出来,会得到一个很大的数值,会对最终的结果产生更大的影响,但这样有利于我们进行分类吗?不利于的。
我们更希望的是找到这样的一种词,在某一个类别的文章中,出现的次数很多,但是在其他类别的文章当中出现很少或者几乎不出现。这样的词更有利于我们分类。我们把这样的词叫做 关键词 。
我们怎么才能找到一种方法,很方便的一下子看出来这个词是关键词呢?这就是我们接下来要介绍的另一种方法 TfidfVectorizer,这种方法就可以自动的找出哪一个词更为重要,哪一个词有利于对我们分类结果的显示。
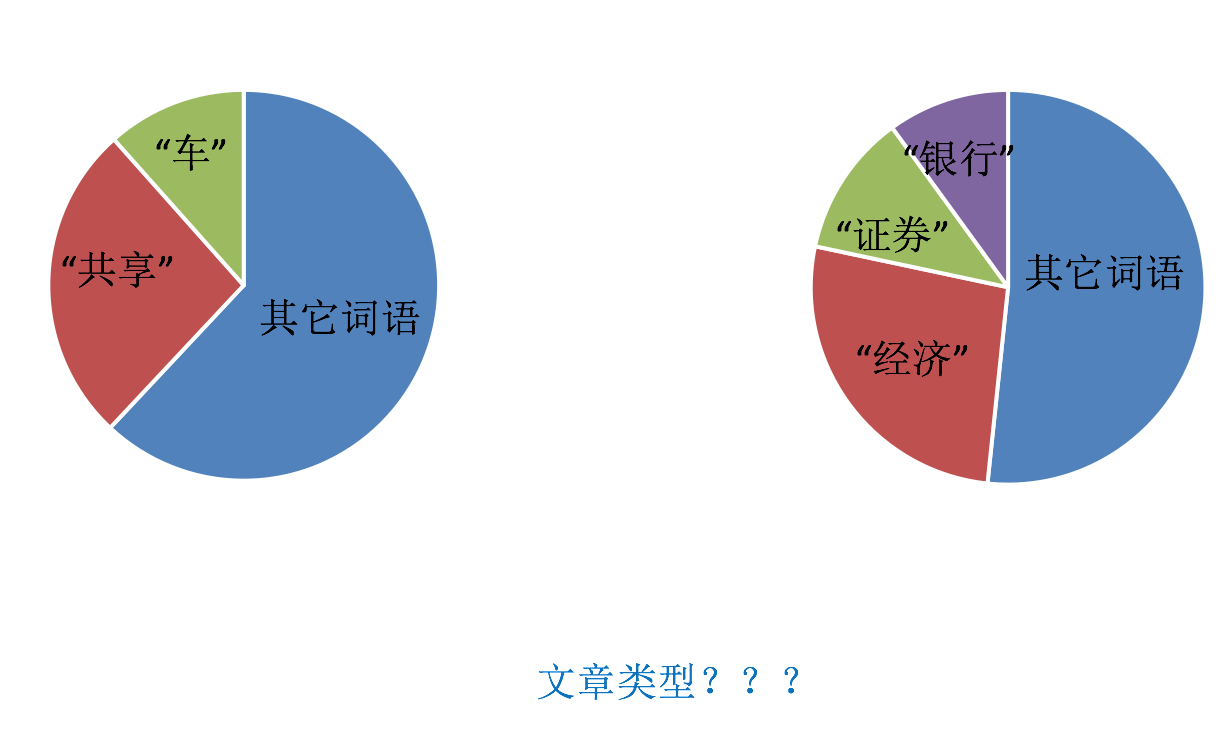
比如说,看下图,有两篇文章,根据这两篇文章出现的词 在整篇文章的占比情况 来分析这两篇文章属于什么类型的文章。
我们看左边这个文章,在一篇文章当中大量的出现 “车” 和 “共享” ,很可能在讲共享单车或者共享汽车,那么这篇文章很有可能是属于科技类或者互联网类别的。
右边的文章大量的出现 “银行”、“证券”、“经济”,很有可能这篇文章是属于财经、金融类型的文章。
我们看到像找到这些词,它们在自己的类别当中会出现很多次,“车” 、“共享” 一般不会出现在财经、金融类的文章当中,而 “银行”、“证券”、“经济” 也一般不会出现在科技类的文章当中。我们更希望找到这样的关键词。
方法2:TfidfVectorizer
5、Tf-idf文本特征提取
- TF-IDF的主要思想是:如果某个词或短语在一篇文章中出现的概率高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。
TF-IDF作用:用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
5.1 公式
- 词频(term frequency,
tf)指的是某一个给定的词语在该文件中出现的频率。词频=词出现次数 / 文件总词数 - 逆向文档频率(inverse document frequency,
idf)是一个词语普遍重要性的度量。某一特定词语的idf,可以由总文件数目除以包含该词语之文件的数目(语料库),再将得到的商取以10为底的对数得到 TF-IDF= tf * idf
最终得出结果可以理解为重要程度。
词频怎么计算?举个例子:现在有两个词“经济”、“非常”
总共有1000篇文章作为语料库,
其中100篇文章 都有 “非常”
而只有 10篇文章 有 “经济”
2篇文章:文章A(100词) : 10次“经济”
tf:10/100 = 0.1
idf:lg 1000/10 = 2
TF-IDF:0.2
文章B(100词) : 10次“非常”
tf:10/100 = 0.1
idf: log 10 1000/100 = 1
TF-IDF:0.1
对数
2 ^ 3 = 8
log 2 8 = 3
log 10 10 = 1
注意:假如一篇文件的总词语数是100个,而词语"非常"出现了5次,那么"非常"一词在该文件中的词频(TF)就是5/100=0.05。而计算文件频率(IDF)的方法是以文件集的文件总数,除以出现"非常"一词的文件数。所以,如果"非常"一词在10,000份文件出现过,而文件总数是10,000,000份的话,其逆向文件频率就是lg(10,000,000 / 1,0000)=3。最后"非常"对于这篇文档的tf-idf的分数为0.05 * 3=0.15
5.2 API
sklearn.feature_extraction.text.TfidfVectorizer(stop_words=None,...)- 返回词的权重矩阵
- TfidfVectorizer.fit_transform(X)
- X:文本或者包含文本字符串的可迭代对象
- 返回值:返回sparse矩阵
- TfidfVectorizer.inverse_transform(X)
- X:array数组或者sparse矩阵
- 返回值:转换之前数据格式
- TfidfVectorizer.get_feature_names()
- 返回值:单词列表
- TfidfVectorizer.fit_transform(X)
- 返回词的权重矩阵
5.3 案例
拿上一个案例的代码把 CountVectorizer 改成 TfidfVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
def cut_words(text):
"""
进行中文分词
"我爱北京天安门" ————> "我 爱 北京 天安门"
:param text:
:return:text
"""
return " ".join(jieba.cut(text))
def tfidf_demo():
"""
用TF-IDF的方法进行文本特征抽取
:return:
"""
data = ["一种还是一种沉溺在“如果情况不同又会发生什么”的设想里,绝对是让人精神失常的不二法门。",
"我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。",
"如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
new_data = []
# 1.将中文文本进行分词
for sent in data:
new_data.append(cut_words(sent))
# print(new_data)
# 2、实例化一个转换器类
# transfer = TfidfVectorizer()
transfer = TfidfVectorizer(stop_words=["一种", "所以"]) # 指定的词语去掉,不作为特征
# 3、调用fit_transform
data_final = transfer.fit_transform(new_data)
print('文本特征抽取的结果:\n', data_final.toarray())
# print("返回特征名字:\n", transfer.get_feature_names())
print("返回特征名字:\n", transfer.get_feature_names_out())
return None
if __name__ == '__main__':
tfidf_demo()
返回结果:
文本特征抽取的结果:
[[0.30746099 0. 0.30746099 0. 0. 0.
0.30746099 0. 0. 0. 0.30746099 0.
0. 0. 0. 0.23383201 0. 0.30746099
0. 0. 0. 0. 0.30746099 0.
0. 0. 0.30746099 0.30746099 0. 0.30746099
0. 0.30746099 0. ]
[0. 0. 0. 0.2410822 0. 0.
0. 0.2410822 0.2410822 0.2410822 0. 0.
0. 0. 0. 0. 0.2410822 0.
0.55004769 0. 0.2410822 0. 0. 0.48216441
0. 0. 0. 0. 0. 0.
0.2410822 0. 0.2410822 ]
[0. 0.15980722 0. 0. 0.6392289 0.47942167
0. 0. 0. 0. 0. 0.15980722
0.15980722 0.15980722 0.15980722 0.12153751 0. 0.
0.12153751 0.15980722 0. 0.15980722 0. 0.
0.31961445 0.15980722 0. 0. 0.15980722 0.
0. 0. 0. ]]
返回特征名字:
['不二法门' '不会' '不同' '之前' '了解' '事物' '什么' '光是在' '几百万年' '发出' '发生' '取决于' '只用'
'含义' '如何' '如果' '宇宙' '情况' '我们' '方式' '星系' '某样' '沉溺在' '看到' '真正' '秘密' '精神失常'
'绝对' '联系' '设想' '过去' '还是' '这样']
我们看到有的是0,有的是0.3、0.2,有个比较大的0.55 。这样的一些数值,大的就能体现出这个词是比较重要的,比较适合用于进行分类的,更具有分类意义的词。我们会在以后如果用传统的机器学习算法sklearn进行文本的处理,那么你就会经常用到 Tfidf 这样的文本特征抽取的方法。
6、Tf-idf的重要性
分类机器学习算法进行文章分类中前期数据处理方式
2.4 特征预处理
- 目标
- 了解数值型数据、类别型数据特点
- 应用MinMaxScaler实现对特征数据进行归一化
- 应用StandardScaler实现对特征数据进行标准化
什么是特征预处理?
2.4.1 什么是特征预处理
# scikit-learn 官网给的解释
provides several common utility functions and transformer classes to change raw feature vectors into a representation that is more suitable for the downstream estimators.
翻译过来:通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
可以通过上面那张图来理解
1、包含内容
- 数值型数据的无量纲化:
- 归一化
- 标准化
2、特征预处理API
sklearn.preprocessing
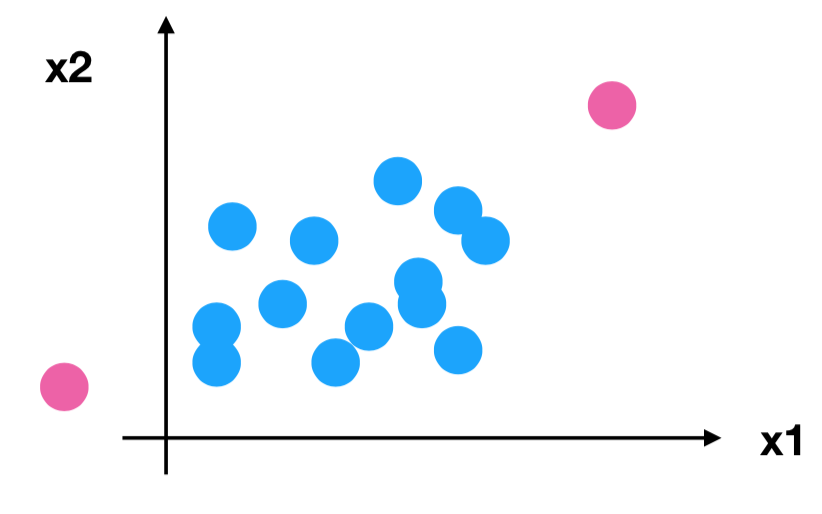
为什么我们要进行归一化 / 标准化?
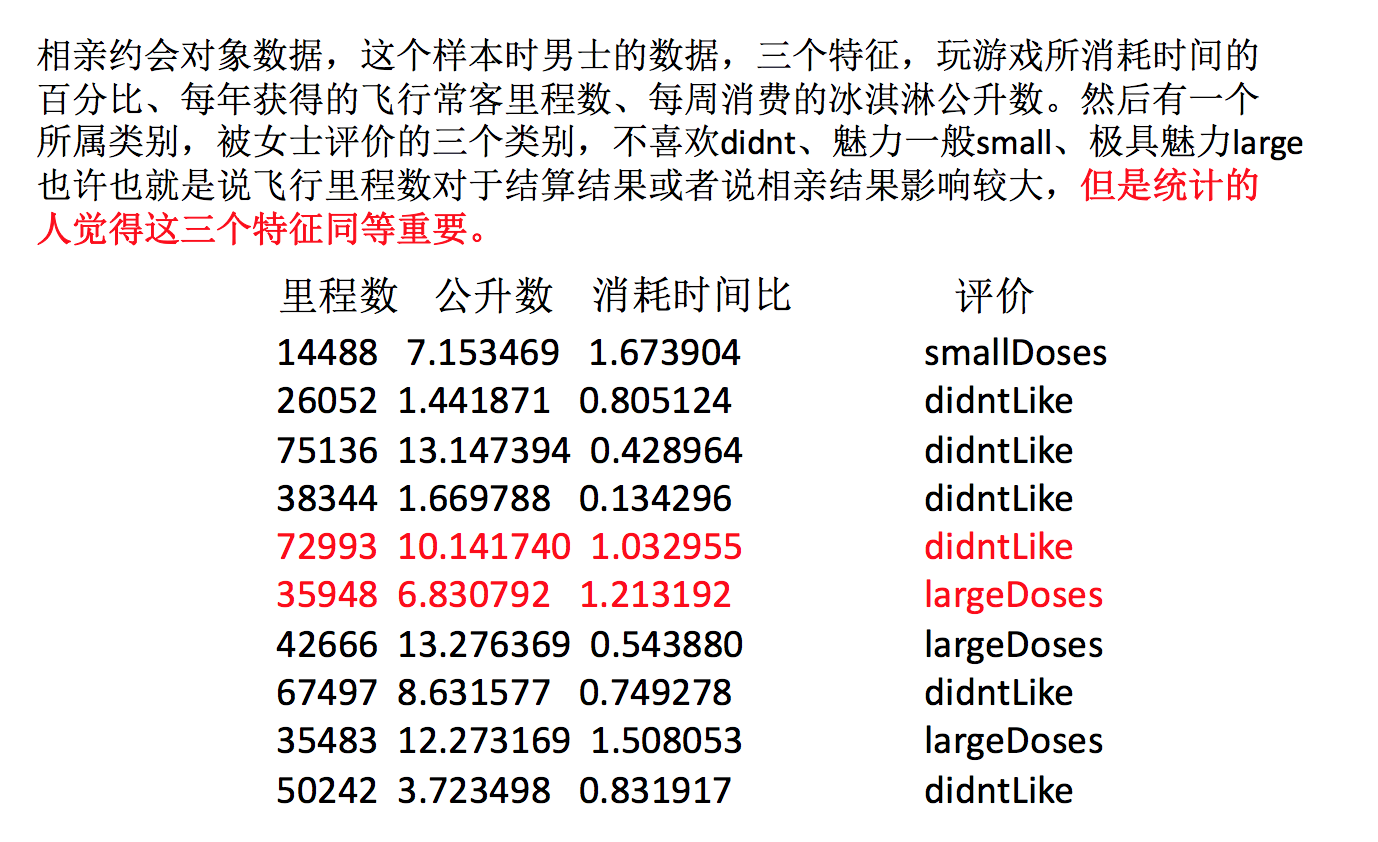
- 特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级,容易影响(支配)目标结果,使得一些算法无法学习到其它的特征
约会对象数据
我们需要用到一些方法进行无量纲化,使不同规格的数据转换到同一规格
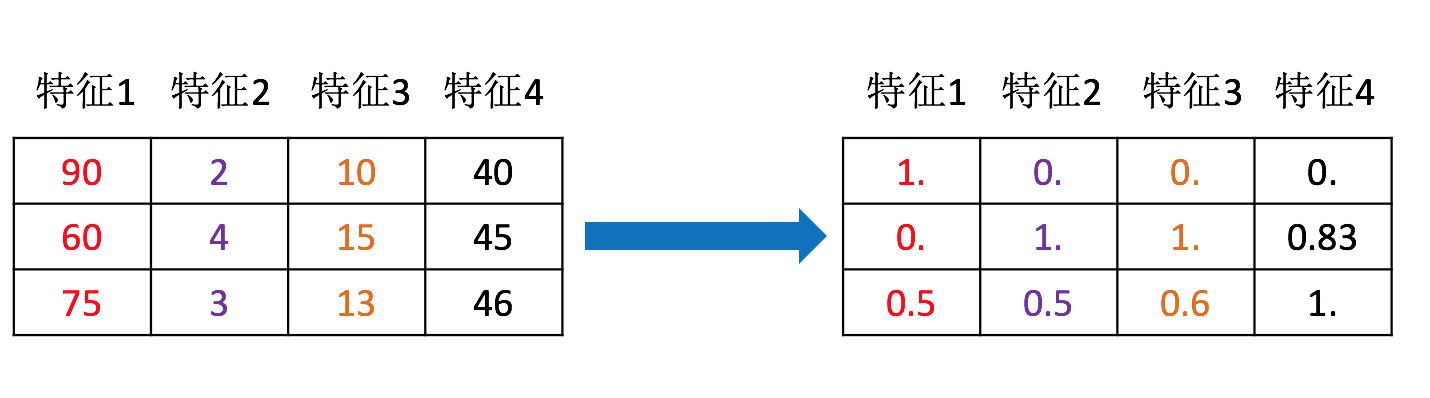
2.4.2 归一化
1、定义
通过对原始数据进行变换把数据映射到 一个固定的区间(默认为[0,1]) 之间。
2、公式
作用于每一列,max为一列的最大值,min为一列的最小值,那么X’’为最终结果,mx,mi分别为指定区间值默认mx为1,mi为0
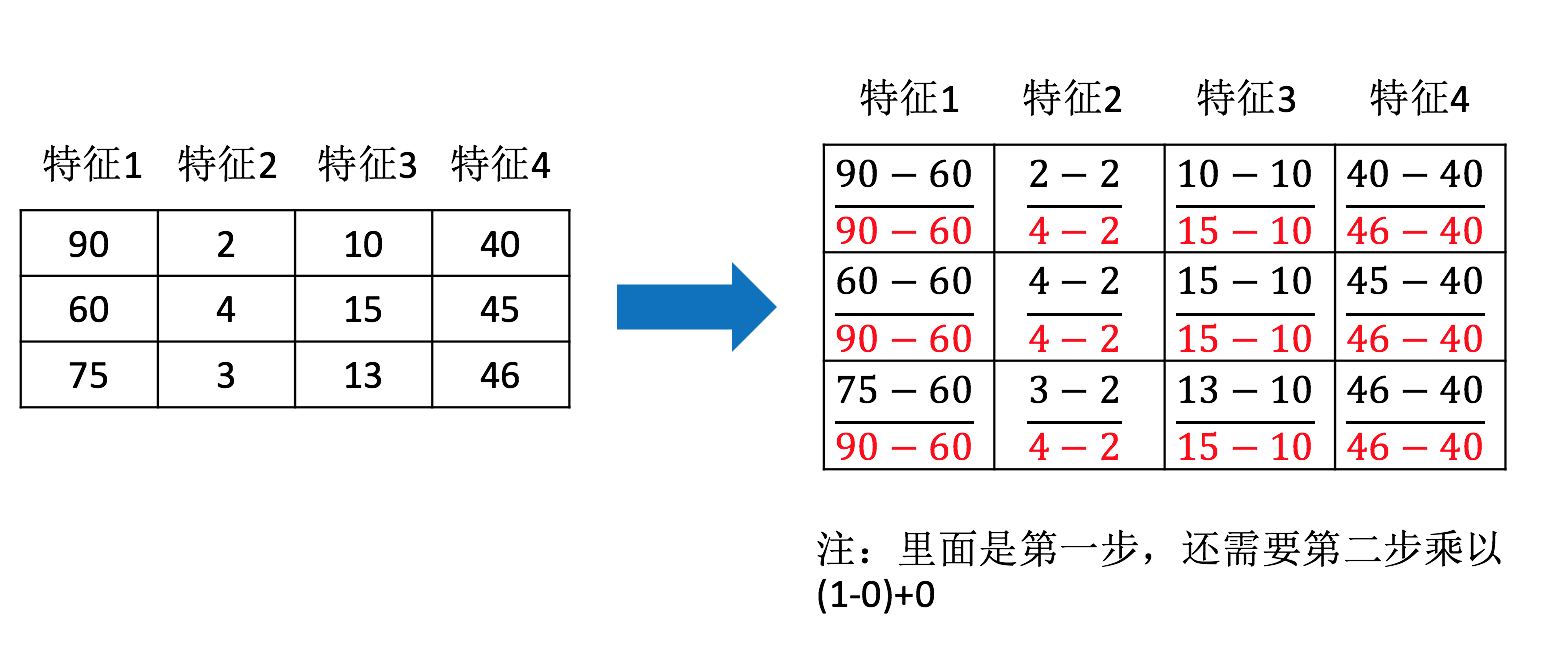
那么怎么理解这个过程呢?我们通过一个例子
特征1 这一列最大值是90、最小值是60,放到指定区间 [0,1]
X’ = (90-60) / (90-60) =1
X’’ = 1 * (1-0) + 0 = 1
3、API
- sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
Scaler 缩放器
MinMaxScaler 最小值最大值放缩- MinMaxScalar.fit_transform(X)
- X:numpy array格式(ndarray)的数据 [n_samples,n_features]
形状是二维数组 [ 样本数, 特征数 ]
- X:numpy array格式(ndarray)的数据 [n_samples,n_features]
- 返回值:转换后的形状相同的array
- MinMaxScalar.fit_transform(X)
4、数据计算
网盘链接:链接:https://pan.baidu.com/s/1za_R-yrzpphy4sVd2JlelA?pwd=6666
提取码:6666
我们对以下数据进行运算,在dating.txt中。保存的就是之前的约会对象数据
milage,Liters,Consumtime,target
40920,8.326976,0.953952,3
14488,7.153469,1.673904,2
26052,1.441871,0.805124,1
75136,13.147394,0.428964,1
38344,1.669788,0.134296,1
72993,10.141740,1.032955,1
35948,6.830792,1.213192,3
42666,13.276369,0.543880,3
67497,8.631577,0.749278,1
35483,12.273169,1.508053,3
50242,3.723498,0.831917,1
- 分析
1、实例化MinMaxScalar
2、通过fit_transform转换
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
def minmax_demo():
"""
归一化
:return:
"""
# 1.获取数据
data = pd.read_csv('dating.txt') # 读取文件用pandas是最方便的
# print("data:\n", data) # <class 'pandas.core.frame.DataFrame'>
data = data.iloc[:, :3] # 每行前三列取到
# milage Liters Consumtime
# 飞机里程数 公升数 消耗时间比
print("data:\n", data)
# 2.实例化一个转换器类
transfer = MinMaxScaler() # 默认[0,1]
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print("data_new:\n", data_new)
# 飞机里程数很大、公升数很小,但我们看最终转换的效果都在[0,1]区间内,转化就完成了
return None
if __name__ == '__main__':
minmax_demo()
返回结果:
data:
milage Liters Consumtime
0 40920 8.326976 0.953952
1 14488 7.153469 1.673904
2 26052 1.441871 0.805124
3 75136 13.147394 0.428964
4 38344 1.669788 0.134296
.. ... ... ...
995 11145 3.410627 0.631838
996 68846 9.974715 0.669787
997 26575 10.650102 0.866627
998 48111 9.134528 0.728045
999 43757 7.882601 1.332446
[1000 rows x 3 columns]
data_new:
[[0.44832535 0.39805139 0.56233353]
[0.15873259 0.34195467 0.98724416]
[0.28542943 0.06892523 0.47449629]
...
[0.29115949 0.50910294 0.51079493]
[0.52711097 0.43665451 0.4290048 ]
[0.47940793 0.3768091 0.78571804]]
试一下其他范围, 比如 [2,3]
transfer = MinMaxScaler(feature_range=(2, 3))
那么它这个结果就是[2-3]这个范围
data_new:
[[2.44832535 2.39805139 2.56233353]
[2.15873259 2.34195467 2.98724416]
[2.28542943 2.06892523 2.47449629]
...
[2.29115949 2.50910294 2.51079493]
[2.52711097 2.43665451 2.4290048 ]
[2.47940793 2.3768091 2.78571804]]
Process finished with exit code 0
缺点:问题:如果数据中异常点较多,会有什么影响?
异常值通常在最大的地方或者最小的地方突然出现一个值,所以异常值一般是最大值或者最小值。
我们归一化的时候,就是用最大值最小值去求的,一旦我们最大值或者最小值是一个异常值,这么一计算,最终归一化的结果也不会太准。
5、归一化总结
注意最大值最小值是变化的,另外,最大值与最小值非常容易受异常点影响,所以这种方法鲁棒性较差,只适合传统精确小数据场景。
鲁棒性:其实就是 健壮性、稳定性
怎么办?
2.4.3 标准化
1、定义
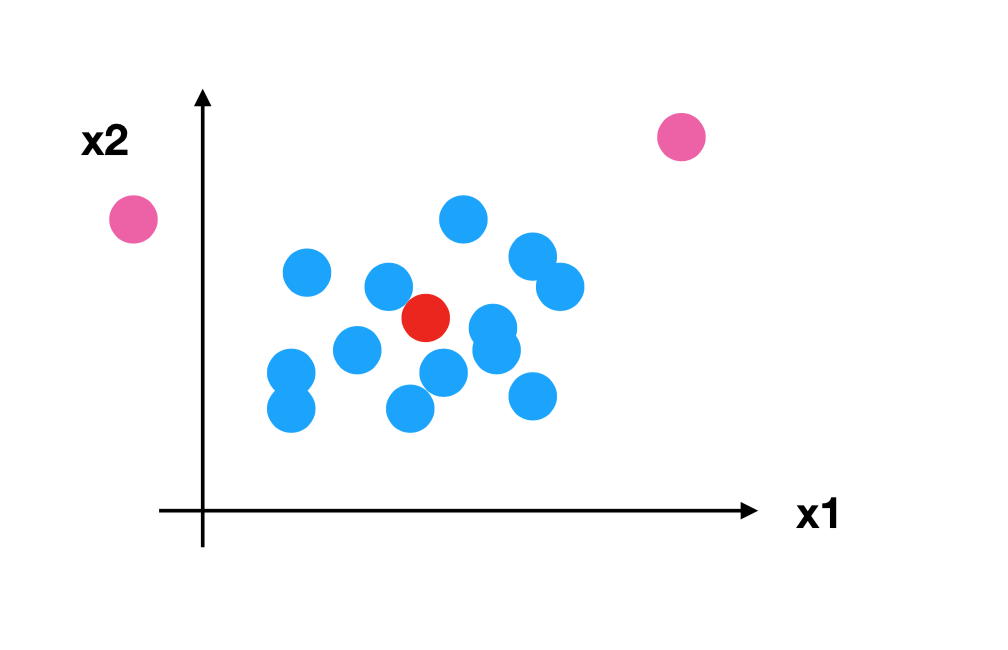
通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内。
2、公式
作用于每一列,mean为平均值,σ为标准差
所以回到刚才异常点的地方,我们再来看看标准化
标准差 衡量的 离散程度(集中程度)。
- 对于归一化来说:如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
- 对于标准化来说:如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大,从而方差改变较小。
3、API
- sklearn.preprocessing.StandardScaler( )
Standard 标准,Scaler 放缩器- 处理之后每列来说所有数据都聚集在均值0附近标准差差为1
- StandardScaler.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后的形状相同的array
4、数据计算
同样对上面的数据进行处理
- 分析
1、实例化StandardScaler
2、通过fit_transform转换
import pandas as pd
from sklearn.preprocessing import StandardScaler
def stand_demo():
"""
标准化
:return:
"""
# 1.获取数据
data = pd.read_csv('dating.txt') # 读取文件用pandas是最方便的
# print("data:\n", data) # <class 'pandas.core.frame.DataFrame'>
data = data.iloc[:, :3] # 每行前三列取到
# milage Liters Consumtime
# 飞机里程数 公升数 消耗时间比
# print("data:\n", data)
# 2.实例化一个转换器类
transfer = StandardScaler()
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print("data_new:\n", data_new)
return None
if __name__ == '__main__':
stand_demo()
结果:
data_new:
[[ 0.33193158 0.41660188 0.24523407]
[-0.87247784 0.13992897 1.69385734]
[-0.34554872 -1.20667094 -0.05422437]
...
[-0.32171752 0.96431572 0.06952649]
[ 0.65959911 0.60699509 -0.20931587]
[ 0.46120328 0.31183342 1.00680598]]
这样返回过来的结果同样也是有无量纲化的效果,飞机里程数很大、公升数很小, 但我们经过这样回答转换之后,都是在均数为0标准差为1的附近, 每一列都有这样的一个特点,就进行了无量纲化处理,也就达到了我们的目的,并且还不容易受到异常点的影响。
如果需要对特征进行无量纲化处理,我们一般用的就是标准化。
5、标准化总结
在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景。
2.5 特征降维
- 目标
- 知道特征选择的嵌入式、过滤式以及包裹氏三种方式
- 应用VarianceThreshold实现删除低方差特征
- 了解相关系数的特点和计算
- 应用相关性系数实现特征选择
2.5.1 降维
降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程。
降维降的对象 是二维数组,几行代表有几个样本,几列代表有几个特征。我们现在要做的特征工程的特征降维的话,也是对二维数组进行处理的,所以我们明确我们的处理对象是二维数组,这里的降维到底降维降的是什么呢?降维的其实是我们特征的个数,也就是列数。
降维的要求:我们不仅要降低特征的个数,还要求最终的效果是 要求特征与特征之间不相关。这样的话有一个好处,如果这组特征里面有大量的相关的特征的话,这个会有冗余信息,这就导致特征太多了,本来不需要这么多,由于相关的特征太多,造成数据的冗余,如果数据量很大的话,我们处理起来就更不方便了。
-
降低随机变量的个数
比如说一开始是一个三维的空间,我们的数分布在三维当中,我们现在不想让它维数这么多,想让它维数少一点,降成二维的,相当于把它转成平面当中,这样的一个转换就是我们降维做的事情。 -
相关特征(correlated feature)
- 相对湿度与降雨量之间的相关
- 等等
正是因为在进行训练的时候,我们都是使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强,对于算法学习预测会影响较大。所以我们才要进行降维。
2.5.2 降维的两种方式
- 特征选择
- 主成分分析(可以理解一种特征提取的方式)
2.5.3 什么是特征选择
1 定义
数据中包含冗余或无关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。
2 方法
- Filter(过滤式):主要探究特征本身特点、特征与特征和目标值之间关联
- 方差选择法:低方差特征过滤
- 相关系数 - 特征与特征之间的相关程度
- Embedded (嵌入式):算法自动选择特征(特征与目标值之间的关联)
- 决策树:信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
对于Embedded方式,只能在讲解算法的时候在进行介绍,更好的去理解
3 模块
sklearn.feature_selection
4 过滤式
4.1 低方差特征过滤
删除低方差的一些特征,前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。
- 特征方差小:某个特征大多样本的值比较相近
- 特征方差大:某个特征很多样本的值都有差别
在概率论和统计方差是衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
4.1.1 API
- sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
Variance方差 Threshold 阈值、临界值- threshold 临界值,低于临界值的特征都给他删掉,默认是0,意思是这列特征都一样的话就给他删掉。
- 删除所有低方差特征
- Variance.fit_transform(X)
- X:numpy array格式的数据 [n_samples,n_features]
- 返回值:训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
4.1.2 数据计算
网盘链接:链接:https://pan.baidu.com/s/1za_R-yrzpphy4sVd2JlelA?pwd=6666
提取码:6666
我们对某些股票的指标特征之间进行一个筛选,数据在"factor_regression_data/factor_returns.csv"文件当中,除去’index,‘date’,'return’列不考虑 (这些类型不匹配,也不是所需要指标)
一共这些特征
pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expense
特征太多了,想做一个特征选择,就用删除低方差特征来做。
index,pe_ratio,pb_ratio,market_cap,return_on_asset_net_profit,du_return_on_equity,ev,earnings_per_share,revenue,total_expense,date,return
0,000001.XSHE,5.9572,1.1818,85252550922.0,0.8008,14.9403,1211444855670.0,2.01,20701401000.0,10882540000.0,2012-01-31,0.027657228229937388
1,000002.XSHE,7.0289,1.588,84113358168.0,1.6463,7.8656,300252061695.0,0.326,29308369223.2,23783476901.2,2012-01-31,0.08235182370820669
2,000008.XSHE,-262.7461,7.0003,517045520.0,-0.5678,-0.5943,770517752.56,-0.006,11679829.03,12030080.04,2012-01-31,0.09978900335112327
3,000060.XSHE,16.476,3.7146,19680455995.0,5.6036,14.617,28009159184.6,0.35,9189386877.65,7935542726.05,2012-01-31,0.12159482758620697
4,000069.XSHE,12.5878,2.5616,41727214853.0,2.8729,10.9097,81247380359.0,0.271,8951453490.28,7091397989.13,2012-01-31,-0.0026808154146886697
- 分析
1、初始化VarianceThreshold,指定阀值方差
2、调用fit_transform
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
def variance_demo():
"""
过滤低方差特征
:return:
"""
# 1.获取数据
data = pd.read_csv('factor_returns.csv')
# print("data:\n", data)
data = data.iloc[:, 1:-2]
print("data:\n", data)
# 2.实例化一个转换器类
transfer = VarianceThreshold() # 默认threshold = 0.0
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print("data_new\n", data_new, data_new.shape)
return None
if __name__ == '__main__':
variance_demo()
返回结果:
data:
pe_ratio pb_ratio ... revenue total_expense
0 5.9572 1.1818 ... 2.070140e+10 1.088254e+10
1 7.0289 1.5880 ... 2.930837e+10 2.378348e+10
2 -262.7461 7.0003 ... 1.167983e+07 1.203008e+07
3 16.4760 3.7146 ... 9.189387e+09 7.935543e+09
4 12.5878 2.5616 ... 8.951453e+09 7.091398e+09
... ... ... ... ... ...
2313 25.0848 4.2323 ... 1.148170e+10 1.041419e+10
2314 59.4849 1.6392 ... 1.731713e+09 1.089783e+09
2315 39.5523 4.0052 ... 1.789082e+10 1.749295e+10
2316 52.5408 2.4646 ... 6.465392e+09 6.009007e+09
2317 14.2203 1.4103 ... 4.509872e+10 4.132842e+10
[2318 rows x 9 columns]
data_new
[[ 5.95720000e+00 1.18180000e+00 8.52525509e+10 ... 2.01000000e+00
2.07014010e+10 1.08825400e+10]
[ 7.02890000e+00 1.58800000e+00 8.41133582e+10 ... 3.26000000e-01
2.93083692e+10 2.37834769e+10]
[-2.62746100e+02 7.00030000e+00 5.17045520e+08 ... -6.00000000e-03
1.16798290e+07 1.20300800e+07]
...
[ 3.95523000e+01 4.00520000e+00 1.70243430e+10 ... 2.20000000e-01
1.78908166e+10 1.74929478e+10]
[ 5.25408000e+01 2.46460000e+00 3.28790988e+10 ... 1.21000000e-01
6.46539204e+09 6.00900728e+09]
[ 1.42203000e+01 1.41030000e+00 5.91108572e+10 ... 2.47000000e-01
4.50987171e+10 4.13284212e+10]] (2318, 9)
我们可以看到原来是9个特征,现在还是9个特征,说明我们这里面没有方差为0的特征,所以我们阈值设的还是比较苛刻。
transfer = VarianceThreshold(threshold=10)
结果:少了2列
data:
pe_ratio pb_ratio ... revenue total_expense
0 5.9572 1.1818 ... 2.070140e+10 1.088254e+10
1 7.0289 1.5880 ... 2.930837e+10 2.378348e+10
2 -262.7461 7.0003 ... 1.167983e+07 1.203008e+07
3 16.4760 3.7146 ... 9.189387e+09 7.935543e+09
4 12.5878 2.5616 ... 8.951453e+09 7.091398e+09
... ... ... ... ... ...
2313 25.0848 4.2323 ... 1.148170e+10 1.041419e+10
2314 59.4849 1.6392 ... 1.731713e+09 1.089783e+09
2315 39.5523 4.0052 ... 1.789082e+10 1.749295e+10
2316 52.5408 2.4646 ... 6.465392e+09 6.009007e+09
2317 14.2203 1.4103 ... 4.509872e+10 4.132842e+10
[2318 rows x 9 columns]
data_new
[[ 5.95720000e+00 8.52525509e+10 8.00800000e-01 ... 1.21144486e+12
2.07014010e+10 1.08825400e+10]
[ 7.02890000e+00 8.41133582e+10 1.64630000e+00 ... 3.00252062e+11
2.93083692e+10 2.37834769e+10]
[-2.62746100e+02 5.17045520e+08 -5.67800000e-01 ... 7.70517753e+08
1.16798290e+07 1.20300800e+07]
...
[ 3.95523000e+01 1.70243430e+10 3.34400000e+00 ... 2.42081699e+10
1.78908166e+10 1.74929478e+10]
[ 5.25408000e+01 3.28790988e+10 2.74440000e+00 ... 3.88380258e+10
6.46539204e+09 6.00900728e+09]
[ 1.42203000e+01 5.91108572e+10 2.03830000e+00 ... 2.02066110e+11
4.50987171e+10 4.13284212e+10]] (2318, 7)
threshold= 这个设置成什么根据你的需求来设置你的阈值,就可以过滤掉一些不太重要的特征。
4.2 相关系数
相关系数 - 特征与特征之间的相关程度
- 皮尔逊相关系数(Pearson Correlation Coefficient)
- 反映变量之间相关关系密切程度的统计指标
4.2.2 公式计算案例(了解,不用记忆)
-
公式
-
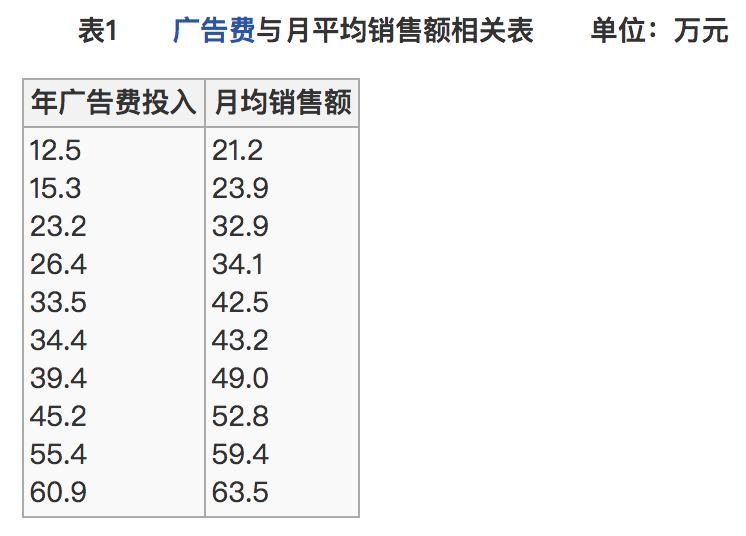
比如说我们计算年广告费投入与月均销售额
那么之间的相关系数怎么计算
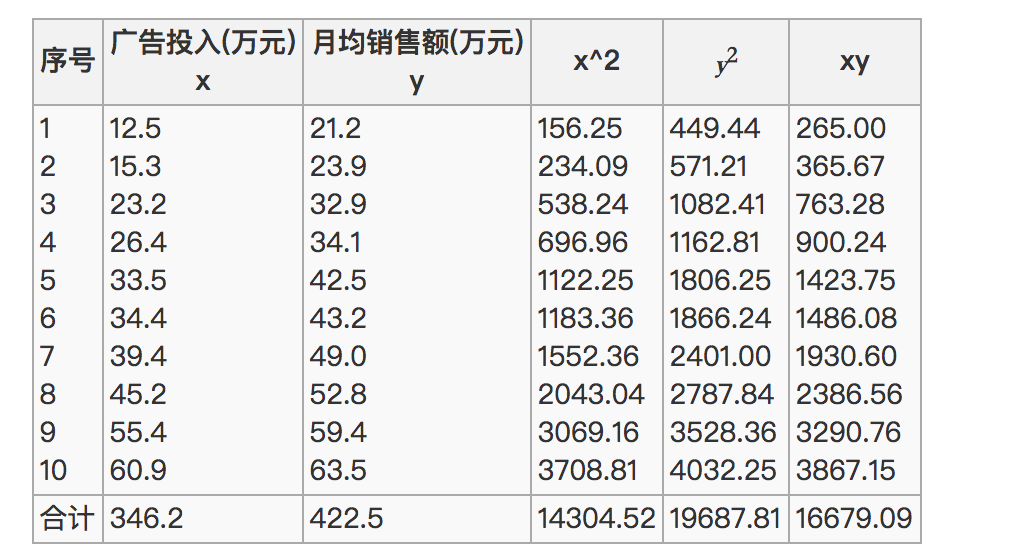
十个样本,所以n=10
最终计算:
所以我们最终得出结论是广告投入费与月平均销售额之间有高度的正相关关系。
4.2.3 特点
相关系数的值介于–1与+1之间,即–1≤ r ≤+1。 其性质如下:
- 当r>0时,表示两变量正相关,r<0时,两变量为负相关
正相关: 其中一个变量在增长,另一个变量也在增长。
负相关:其中一个变量在增长,另一个变量沿着相反的方向在减少。 - 当|r|=1时,表示两变量为完全相关,当r=0时,表示两变量间无相关关系
- 当0<|r|<1时,表示两变量存在一定程度的相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
- 一般可按三级划分:|r|<0.4为低度相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关
这个符号:|r|为r的绝对值, |-5| = 5
4.2.4 API
- from scipy.stats import pearsonr
- pearsonr(x,y)
- x : (N,) array_like
- y : (N,) array_like
- Returns: (Pearson’s correlation coefficient, p-value)
- 返回的第一个就是相关性的值
- pearsonr(x,y)
scipy是一个python开源的数学计算库,可以应用于数学、科学以及工程领域,它是基于numpy的科学计算库。
scipy模块下面有很多包,其中 stats 有 统计分布和函数。
scipy的相关资料
- scipy官网:https://scipy.org
- scipy文档:https://docs.scipy.org/
- scipy源码:https://github.com/scipy/scipy
- scipy中文教程:https://wizardforcel.gitbooks.io/scipy-lecture-notes/content/
安装
pip install scipy
有时候通过pip默认的源来安装包的时候会非常的慢,这时候我们可以通过修改pip的源来提供下载包的速度,有清华源、阿里源、豆瓣源等都可以使用,我这里使用的是清华源设置方法如下:
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scipy
4.2.5 案例:股票的财务指标相关性计算
我们刚才的股票的这些指标进行相关性计算, 假设我们以
factor = ['pe_ratio','pb_ratio','market_cap','return_on_asset_net_profit','du_return_on_equity','ev','earnings_per_share','revenue','total_expense']
这些特征当中的两两进行计算,得出相关性高的一些特征
- 分析
- 两两特征之间进行相关性计算
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
def variance_demo():
"""
过滤低方差特征
:return:
"""
# 1.获取数据
data = pd.read_csv('factor_returns.csv')
# print("data:\n", data)
data = data.iloc[:, 1:-2]
# print("data:\n", data)
# 2.实例化一个转换器类
# transfer = VarianceThreshold() # 默认threshold = 0.0
# transfer = VarianceThreshold(threshold=10)
# 3.调用fit_transform
# data_new = transfer.fit_transform(data)
# print("data_new\n", data_new, data_new.shape)
# 计算某两个变量之间的相关系数
r = pearsonr(data['pe_ratio'], data['pb_ratio'])
print("相关系数:\n", r) # PearsonRResult(statistic=-0.00438932277993627, pvalue=0.8327205496590723)
print("相关系数:\n", r.statistic)
return None
if __name__ == '__main__':
variance_demo()
返回结果:
相关系数:
PearsonRResult(statistic=-0.00438932277993627, pvalue=0.8327205496590723)
相关系数:
-0.00438932277993627
-0.00438932277993627就是他的相关系数,是负相关,并且有点接近于0,也就是说这两者不是特别的相关。
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
def variance_demo():
"""
过滤低方差特征
:return:
"""
# 1.获取数据
data = pd.read_csv('factor_returns.csv')
data = data.iloc[:, 1:-2]
# factor = ['pe_ratio', 'pb_ratio', 'market_cap', 'return_on_asset_net_profit', 'du_return_on_equity', 'ev', 'earnings_per_share', 'revenue', 'total_expense']
factor = list(data.columns)
print("列索引列表 ", factor)
# 计算某两个变量之间的相关系数
# r = pearsonr(data['pe_ratio'], data['pb_ratio'])
# print("相关系数:\n", r) # PearsonRResult(statistic=-0.00438932277993627, pvalue=0.8327205496590723)
# print("相关系数:\n", r.statistic)
for i in range(len(factor)):
for j in range(i, len(factor) - 1):
print(
"指标%s与指标%s之间的相关性大小为%f" % (factor[i], factor[j + 1], pearsonr(data[factor[i]], data[factor[j + 1]])[0]))
return None
if __name__ == '__main__':
variance_demo()
返回结果:
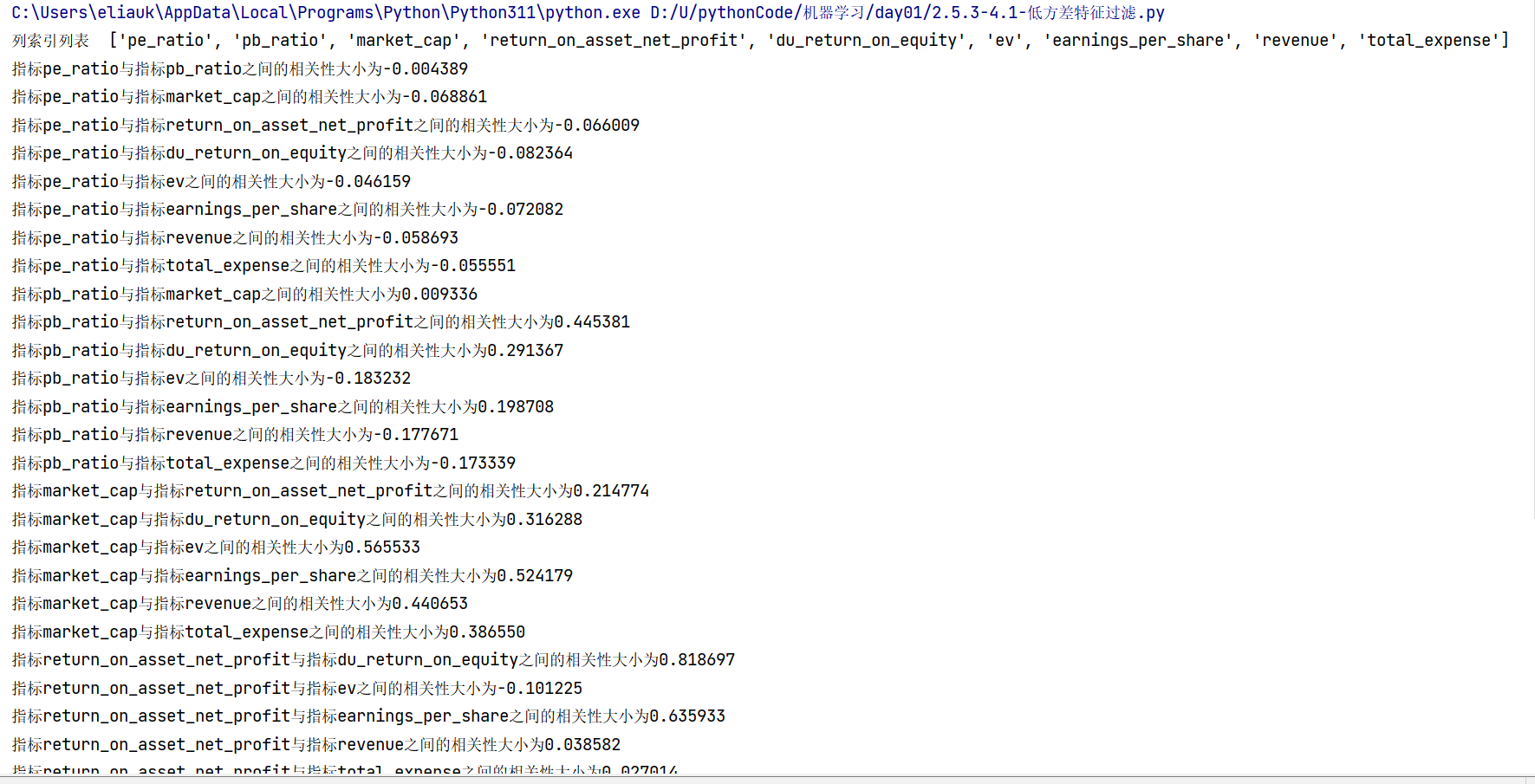
列索引列表 ['pe_ratio', 'pb_ratio', 'market_cap', 'return_on_asset_net_profit', 'du_return_on_equity', 'ev', 'earnings_per_share', 'revenue', 'total_expense']
指标pe_ratio与指标pb_ratio之间的相关性大小为-0.004389
指标pe_ratio与指标market_cap之间的相关性大小为-0.068861
指标pe_ratio与指标return_on_asset_net_profit之间的相关性大小为-0.066009
指标pe_ratio与指标du_return_on_equity之间的相关性大小为-0.082364
指标pe_ratio与指标ev之间的相关性大小为-0.046159
指标pe_ratio与指标earnings_per_share之间的相关性大小为-0.072082
指标pe_ratio与指标revenue之间的相关性大小为-0.058693
指标pe_ratio与指标total_expense之间的相关性大小为-0.055551
指标pb_ratio与指标market_cap之间的相关性大小为0.009336
指标pb_ratio与指标return_on_asset_net_profit之间的相关性大小为0.445381
指标pb_ratio与指标du_return_on_equity之间的相关性大小为0.291367
指标pb_ratio与指标ev之间的相关性大小为-0.183232
指标pb_ratio与指标earnings_per_share之间的相关性大小为0.198708
指标pb_ratio与指标revenue之间的相关性大小为-0.177671
指标pb_ratio与指标total_expense之间的相关性大小为-0.173339
指标market_cap与指标return_on_asset_net_profit之间的相关性大小为0.214774
指标market_cap与指标du_return_on_equity之间的相关性大小为0.316288
指标market_cap与指标ev之间的相关性大小为0.565533
指标market_cap与指标earnings_per_share之间的相关性大小为0.524179
指标market_cap与指标revenue之间的相关性大小为0.440653
指标market_cap与指标total_expense之间的相关性大小为0.386550
指标return_on_asset_net_profit与指标du_return_on_equity之间的相关性大小为0.818697
指标return_on_asset_net_profit与指标ev之间的相关性大小为-0.101225
指标return_on_asset_net_profit与指标earnings_per_share之间的相关性大小为0.635933
指标return_on_asset_net_profit与指标revenue之间的相关性大小为0.038582
指标return_on_asset_net_profit与指标total_expense之间的相关性大小为0.027014
指标du_return_on_equity与指标ev之间的相关性大小为0.118807
指标du_return_on_equity与指标earnings_per_share之间的相关性大小为0.651996
指标du_return_on_equity与指标revenue之间的相关性大小为0.163214
指标du_return_on_equity与指标total_expense之间的相关性大小为0.135412
指标ev与指标earnings_per_share之间的相关性大小为0.196033
指标ev与指标revenue之间的相关性大小为0.224363
指标ev与指标total_expense之间的相关性大小为0.149857
指标earnings_per_share与指标revenue之间的相关性大小为0.141473
指标earnings_per_share与指标total_expense之间的相关性大小为0.105022
指标revenue与指标total_expense之间的相关性大小为0.995845
从中我们得出
- 指标revenue与指标total_expense之间的相关性大小为0.995845
- 指标return_on_asset_net_profit与指标du_return_on_equity之间的相关性大小为0.818697
如果我们想要看两个指标两个字段之间是否有一些线性关系的话,我们用什么来展示能很清楚的发现他们之间的关系?散点图
我们也可以通过画图来观察结果
import matplotlib.pyplot as plt
plt.figure(figsize=(20, 8), dpi=100)
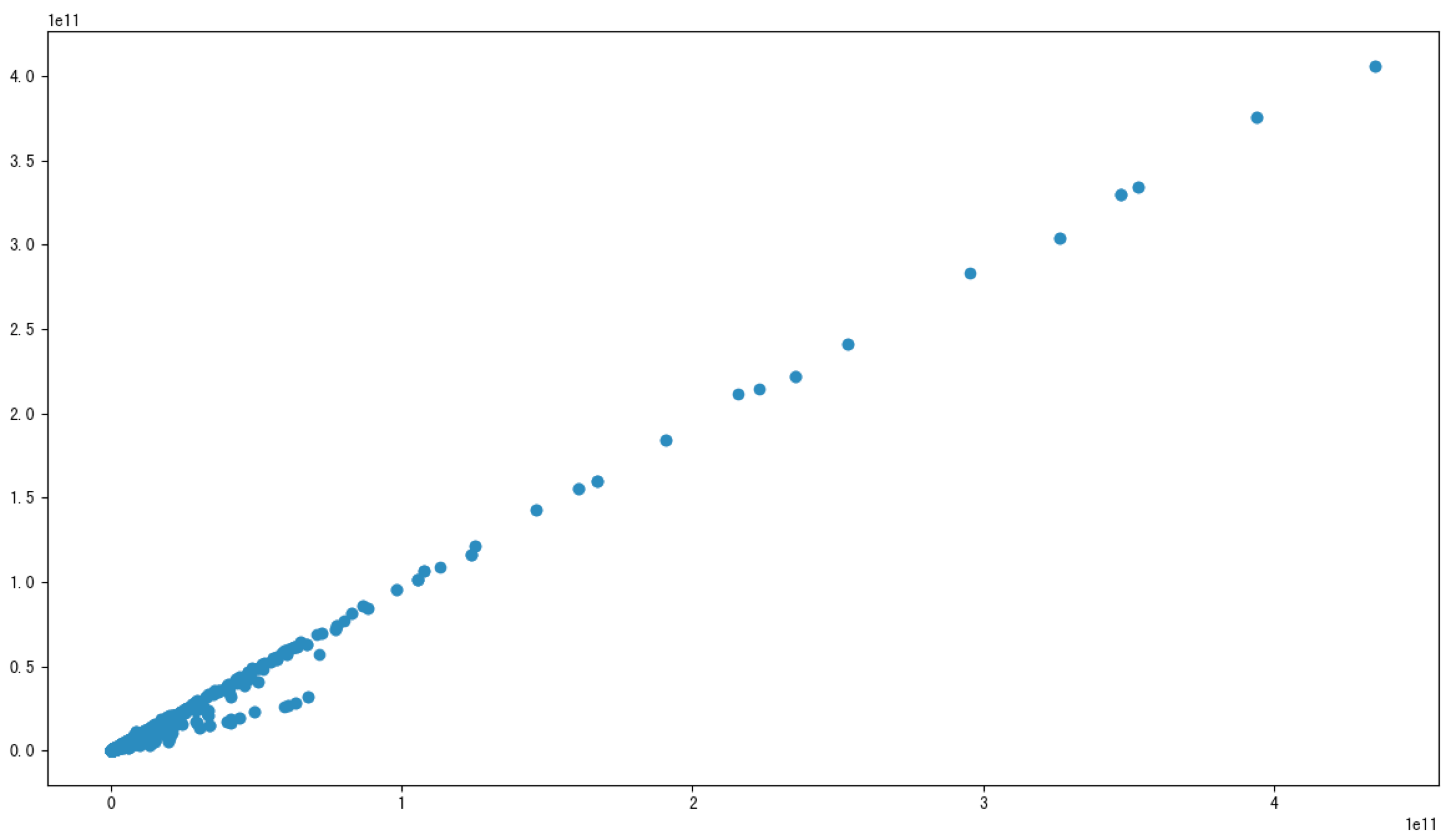
plt.scatter(data['revenue'], data['total_expense'])
plt.show()
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
import matplotlib.pyplot as plt
def variance_demo():
"""
过滤低方差特征
:return:
"""
# 1.获取数据
data = pd.read_csv('factor_returns.csv')
# print("data:\n", data)
data = data.iloc[:, 1:-2]
# print("data:\n", data)
# 2.实例化一个转换器类
# transfer = VarianceThreshold() # 默认threshold = 0.0
# transfer = VarianceThreshold(threshold=10)
# 3.调用fit_transform
# data_new = transfer.fit_transform(data)
# print("data_new\n", data_new, data_new.shape)
# 计算某两个变量之间的相关系数
r1 = pearsonr(data['pe_ratio'], data['pb_ratio'])
print("相关系数:\n", r1) # PearsonRResult(statistic=-0.00438932277993627, pvalue=0.8327205496590723)
# print("相关系数:\n", r1.statistic)
r2 = pearsonr(data['revenue'], data['total_expense'])
print("revenue与total_expense之间的相关性:\n", r2)# PearsonRResult(statistic=0.9958450413136116, pvalue=0.0)
plt.figure(figsize=(20, 8), dpi=100)
plt.scatter(data['revenue'], data['total_expense'])
plt.show()
return None
if __name__ == '__main__':
variance_demo()
可以看到这个图两者非常有相关性,相关性很强,我们计算的结果(revenue与total_expense之间的相关性大小为0.995845)比较接近于1,所以就应证了这两个指标之间相关性比较大。
这两对指标之间的相关性较大,可以做之后的处理,比如合成这两个指标。
特征与特征之间相关性很高,怎么进行特征选择:
1)选取其中一个
2)加权求和
3)主成分分析
2.6 主成分分析
- 目标
- 应用PCA实现特征的降维
- 应用
- 用户与物品类别之间主成分分析
2.6.1 什么是主成分分析(PCA)
-
定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
-
作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
-
应用:回归分析或者聚类分析当中
对于信息一词,在决策树中会进行介绍
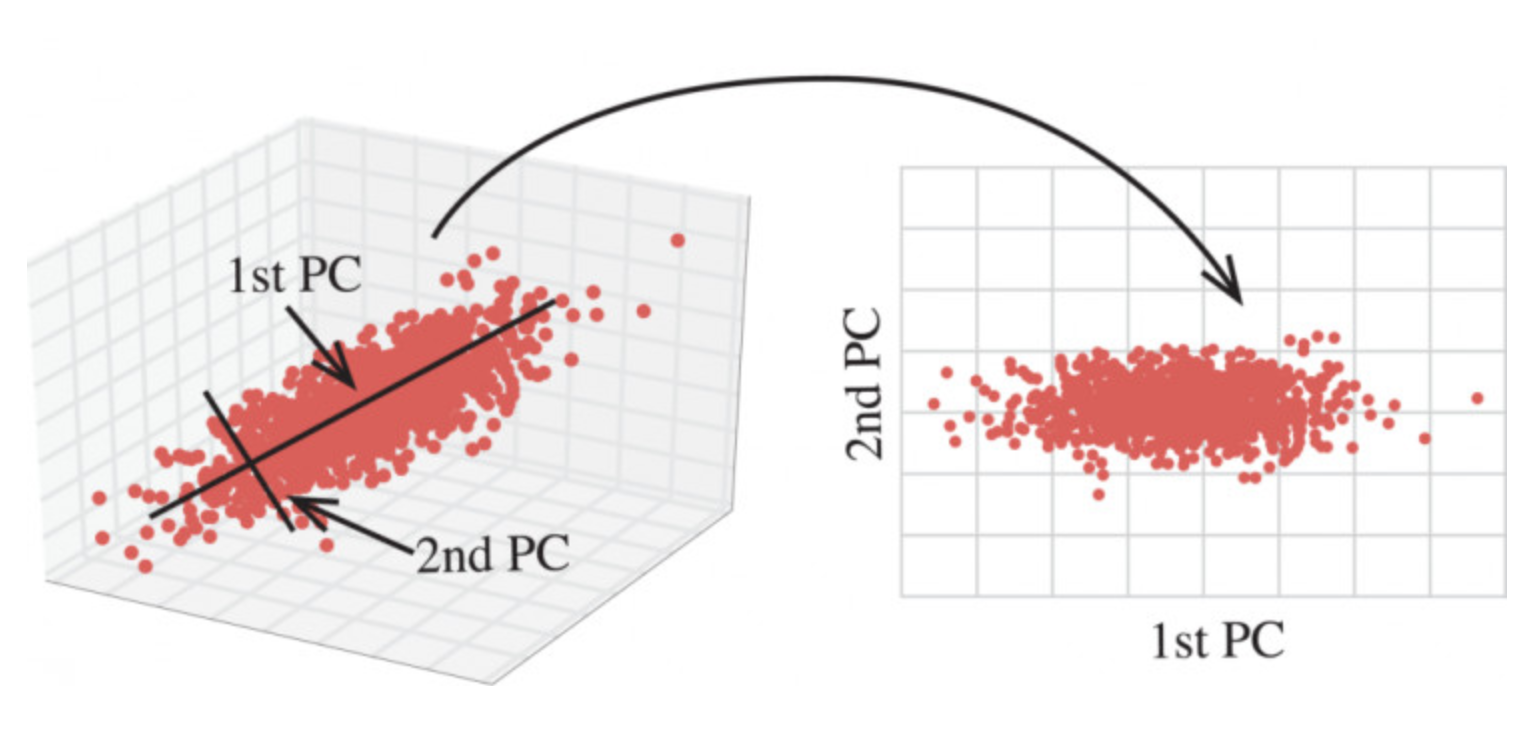
那么更好的理解这个过程呢?我们来看一张图
对一个水壶进行拍摄,日常生活中我们接触到的就是一个三维的空间,如果我们用相机把这个三维空间的图像给记录下来,我们做的这个事情是有点类似于降维,照片是二维的,当我们将现实生活中的场景通过相机记录下来,成为一张照片,其实也就相当于在做降维,将三维降到二维。在这样的一个过程中,那么它就可能会有一些信息的损失,我们如何去衡量在这个过程中信息损失了多少?很直观的检验方法就是我们还能不能通过这个二维的图像能够还原出(知道)它还是一个水壶,所以我们看这四张不同角度去拍摄水壶,哪个还能看出它是一个水壶?第四张能看出,也就意味着第四张照片从三维降到二维这个过程,它损失的信息是最少的,其他图片我们基本看不太出来。如果不告诉你是水壶,它也可能是一个钟等等,所以我们pc 主成分分析,它做的一件什么事情呢?它就是在做降维,并且能够尽可能的去保留最多的信息,让你降维后这个数据还能够保持原有的特征,这就是pc做的事情
1 计算案例理解(了解,无需记忆)
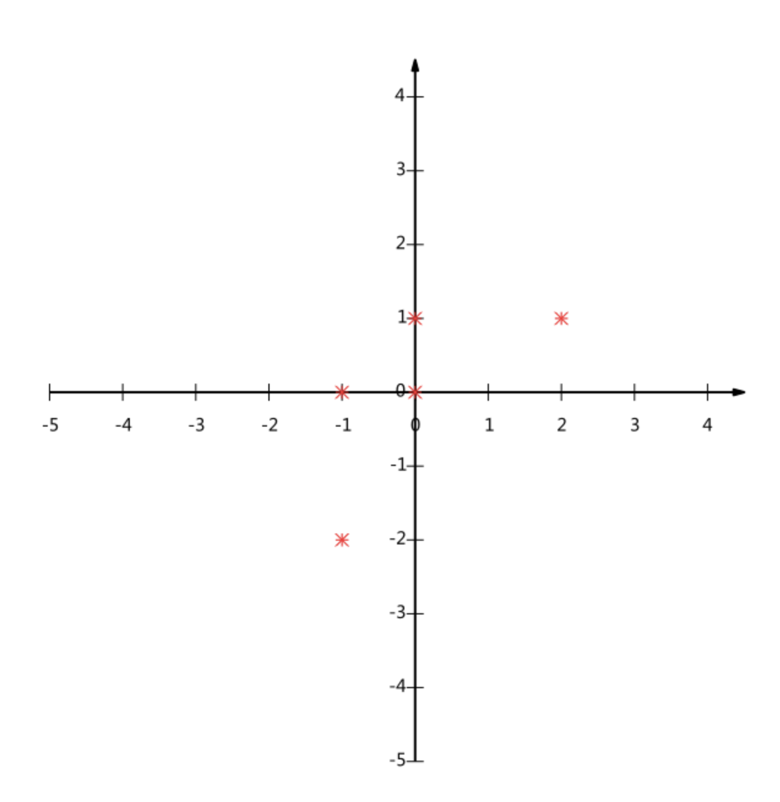
假设对于给定5个点,数据如下
(-1,-2)
(-1, 0)
( 0, 0)
( 2, 1)
( 0, 1)
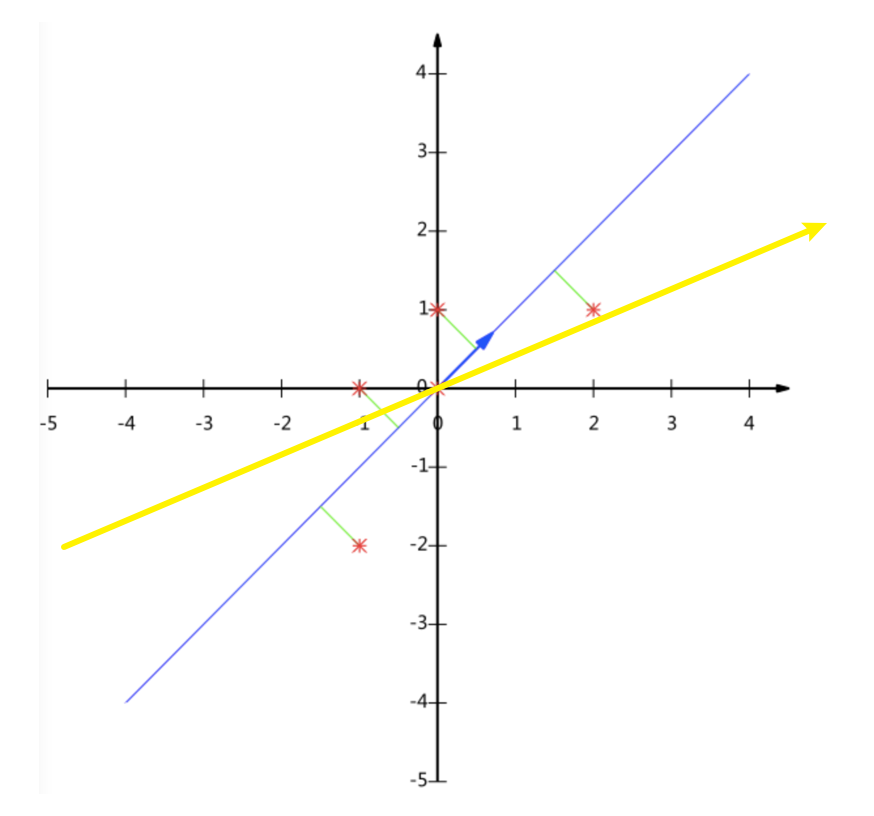
要求:将这个二维的数据简化成一维? 并且损失少量的信息
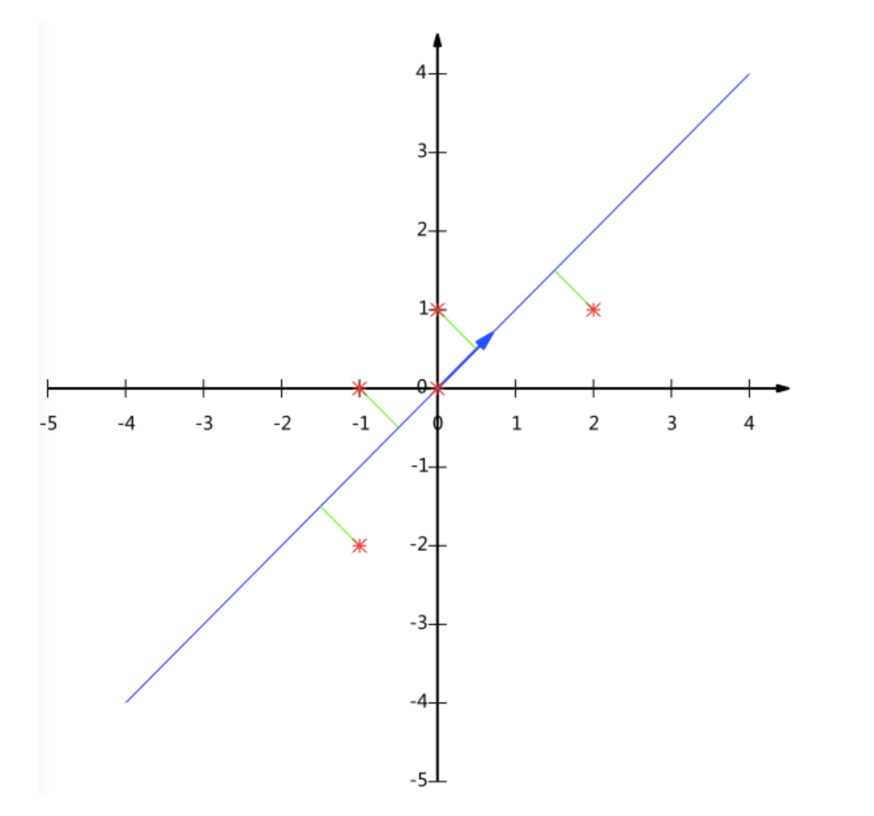
五个点投影到线上,原来是五个点,降维之后还是五个点,并且这五个点到线的距离之和比较少。
虽然说也可以选取其他的线,但是可能这样子的话,它的距离之和加起来会大一点,我们希望能让它的距离之和稍微小一点,这个是pca降维希望做的事情。
这个过程如何计算的呢?找到一个合适的直线,通过一个矩阵运算得出主成分分析的结果(不需要理解)
过程比较复杂,可以去看看pca的原理,可以看看过程,这个方法最终达到一个效果就是前面写的理解这张图就可以了。
2 API
- sklearn.decomposition.PCA(n_components=None)
- 将数据分解为较低维数空间
- n_components:
- 小数:表示保留百分之多少的信息
一般我们用小数比较多 - 整数:减少到多少特征
- 小数:表示保留百分之多少的信息
- PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后指定维度的array,降维、改变形状的array
3 数据计算
先拿个简单的数据计算一下
[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]
from sklearn.decomposition import PCA
def pca_demo():
data = [[2, 8, 4, 5],
[6, 3, 0, 8],
[5, 4, 9, 1]]
# 1.实例化一个转换器类
transfer=PCA(n_components=2)# 四个特征降成两个特征
data_new=transfer.fit_transform(data)
print("data_new:",data_new)
# 2.调用fit_transform
return None
if __name__ == "__main__":
pca_demo()
返回结果:
data_new: [[-3.13587302e-16 3.82970843e+00]
[-5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]
我们试一下传小数:
transfer = PCA(n_components=0.95) # 保留95%的信息
结果:
data_new: [[-3.13587302e-16 3.82970843e+00]
[-5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]
它还是两个特征,说明我们把它降到两个特征,虽然从四个特征降成两个特征好像已经降了一半的特征,但是其实它还保留了原来95%的特征,说明这个方法还是很好的,既降维还保留了尽可能多的信息,这就是PCA降维。
2.6.2 案例:探究用户对物品类别的喜好细分降维
数据如下:
- order_products__prior.csv:订单与商品信息
- 字段:order_id, product_id, add_to_cart_order, reordered
- products.csv:商品信息
- 字段:product_id, product_name, aisle_id, department_id
- orders.csv:用户的订单信息
- 字段:order_id,user_id,eval_set,order_number,….
- aisles.csv:商品所属具体物品类别
- 字段: aisle_id, aisle
1 需求
案例背景:kaggle上一个Instacart公司发布的一个比赛,这个比赛要预测Instacart用户(消费者)下一步将要购买哪些产品。为了完成这样一个目标,首先需要探究这里面的用户,他对这个一些物品的喜好,为了完成这样的一个任务,我们需要准备什么样的数据?
翻译过来相当于我们要找到用户和物品类别之间的关系,首先我们需要有用户,也有他相应购买物品类别的一些信息。首先我们需要找到 user_id 用户id 这样的一个字段,aisle 物品类别字段 。 但是我们发现一个问题啦,user_id在orders.csv数据文件里,而aisle在aisles.csv数据文件当中,要想找到物品类别与用户之间的关系,它们是不是隔得太远了?所以我们想要了我们之前学过的,要合并不同的表把它合并到一张表中,让我们进一步的去解决问题。
分析的结果(接下来我们要完成的3大步骤):
1.需要将用户user_id和aisle放 同一张表当中,我们可以用 合并。
2.找到user_id和aisle这两者之间的关系,那我们可以想到用交叉表和透视表
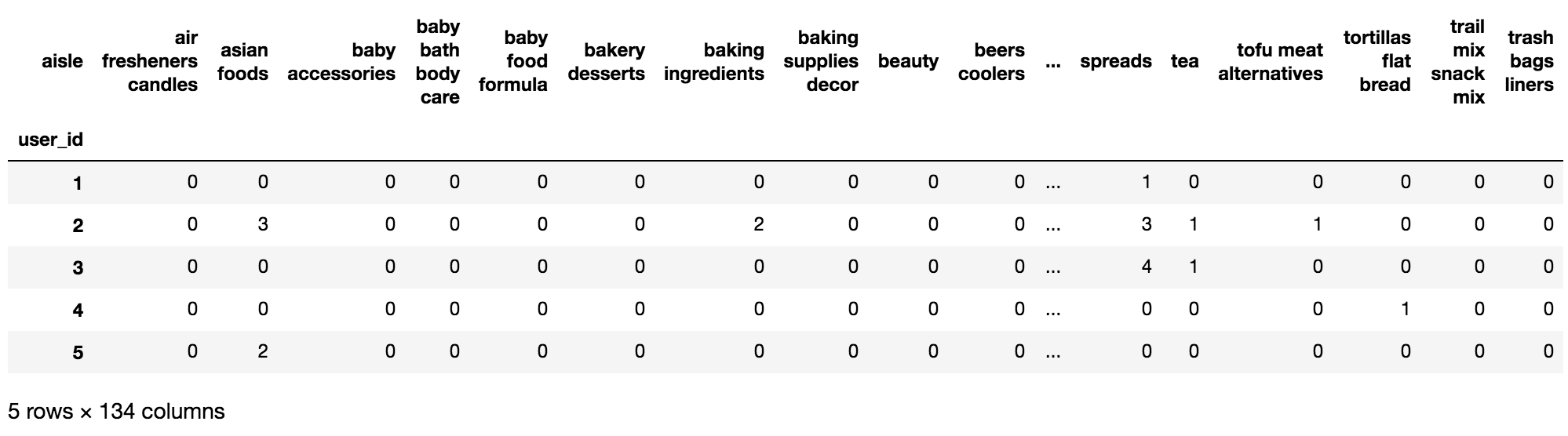
我们说要找到用户和这个物品之间的一个关系,那我们把它们放到一张表中其实还不够,我们还希望能够具体找到这两个变量之间的关系,想将我们最终的结果处理成这样的一种形式。行索引是user_id用户,列索引就是一个个的物品类别,其中就是某一个物品类别购买的数量,比如2号用户购买asian foods亚洲食物有3次,后来还有其他的比如tea茶有一次。
根据这样的一些数据,我们用一些机器学习算法其实就可能分析出这些用户他的一些特性,当我们根据用户购买物品类别的偏好进行进一步的对用户的细分,然后对不同的用户采取不同的营销策略。这是Instacart他想做的一个事情。
3.特征冗余过多,所以要降维了,在这里用PCA降维
我们现在目前学的还是特征工程,也只是对数据进行处理,最终得出消费者要购买哪些产品是我们之后机器学习算法的部分,数据这个部分我们还需要做什么呀?我们看到当我们将这个user_id与aisle放一张表当中并且进行了交叉表和透视表 处理之后是这样一张表,行索引是user_id用户,列索引是我们之后要处理的特征 就是这些物品类别,但是我们发现这些特征有什么样的特点?是不是有大量的0呀,有大量的0就意味着我们的特征有大量的冗余,并且总共有134个特征,之前在做特征工程的时候我们还没遇到这么多特征的。所以我们要做降维,这里就有主成分分析的方法进行降维(PCA降维)。
2 分析
- 合并表,使得user_id与aisle在一张表当中
- 进行交叉表变换
- 进行降维
3 完整代码
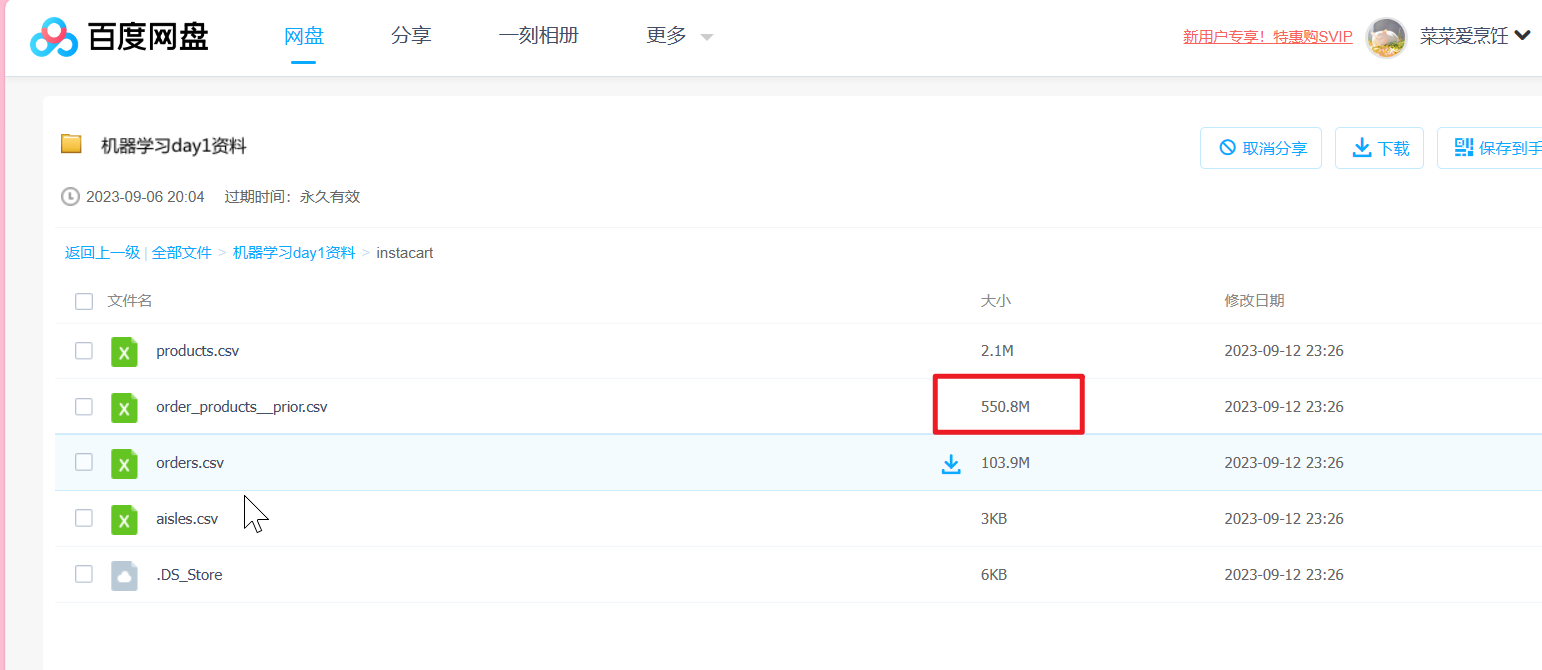
网盘链接:链接:https://pan.baidu.com/s/1za_R-yrzpphy4sVd2JlelA?pwd=6666
提取码:6666
数据在instacart文件夹里
数据还是不小的,其中order_products__prior.csv有550.80M,因为我们接下来要进行数据处理,为了数据展示方便,我们用jupyter notebook来做。
打开cmd,输入jupyter notebook
新建一个文件
代码:
# 1.获取数据
# 2.合并表
# 3.找到user_id与aisle之间的关系
# 4.PCA降维
import pandas as pd
# 1. 获取数据
# 也可以写个for循环去遍历读文件,这样会快一点
order_products = pd.read_csv("./instacart/order_products__prior.csv")
products = pd.read_csv("./instacart/products.csv")
orders = pd.read_csv("./instacart/orders.csv")
aisles = pd.read_csv("./instacart/aisles.csv")
order_products # 订单与商品信息
products #商品信息
orders # 用户的订单信息
aisles # 商品所属具体物品类别
# 2.合并表
# order_products__prior.csv:订单与商品信息
# 字段:order_id, product_id, add_to_cart_order, reordered
# products.csv:商品信息
# 字段:product_id, product_name, aisle_id, department_id
# orders.csv:用户的订单信息
# 字段:order_id,user_id,eval_set,order_number,….
# aisles.csv:商品所属具体物品类别
# 字段: aisle_id, aisle
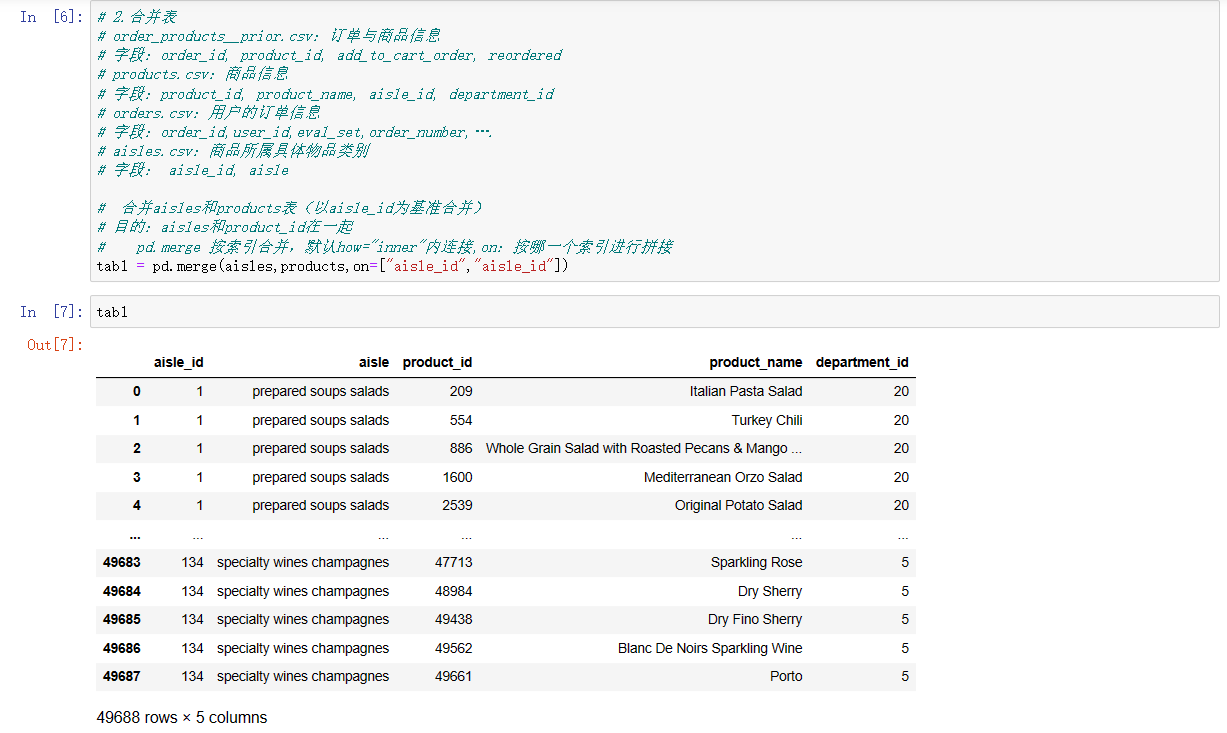
# 合并aisles和products表(以aisle_id为基准合并)
# 目的:aisles和product_id在一起
# pd.merge 按索引合并,默认how="inner"内连接,on:按哪一个索引进行拼接
tab1 = pd.merge(aisles,products,on=["aisle_id","aisle_id"])
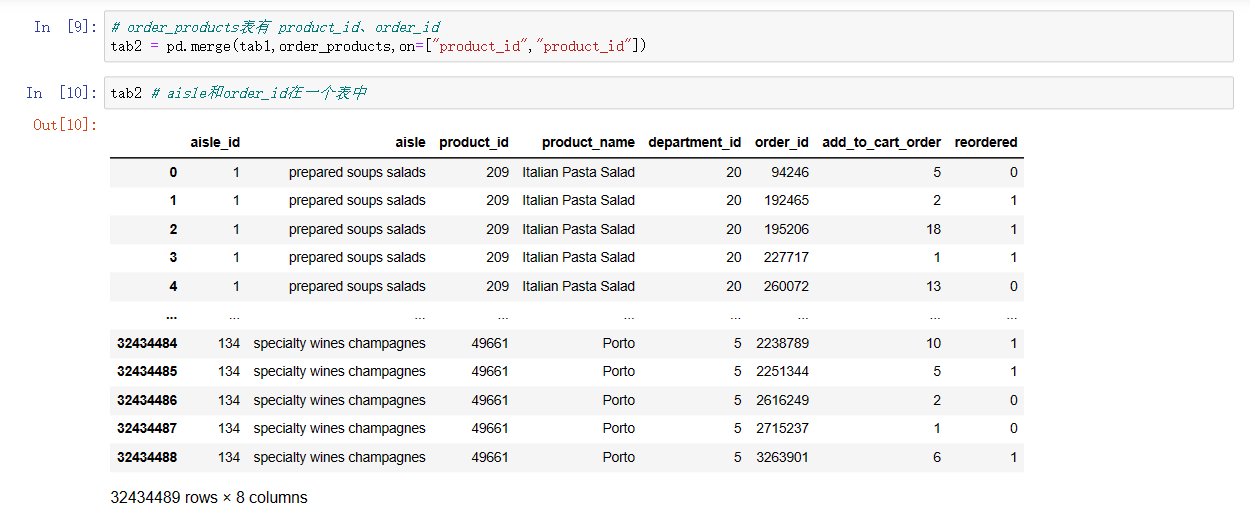
tab1 # order_products表有 product_id、order_id
tab2 = pd.merge(tab1,order_products,on=["product_id","product_id"])
tab2 # aisle和order_id在一个表中
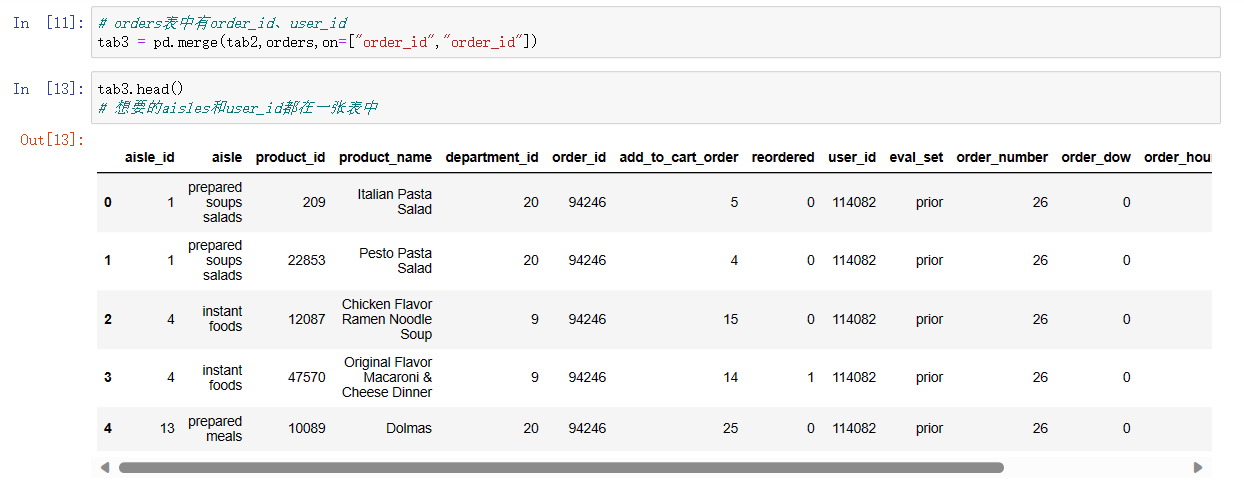
# orders表中有order_id、user_id
tab3 = pd.merge(tab2,orders,on=["order_id","order_id"])
tab3.head() # 想要的aisles和user_id都在一张表中
# 3. 找到 user_id 和 aisle 这两者之间的关系
# 交叉表用于计算一列数据对于另外一列数据的分组个数(寻找两个列之间的关系)
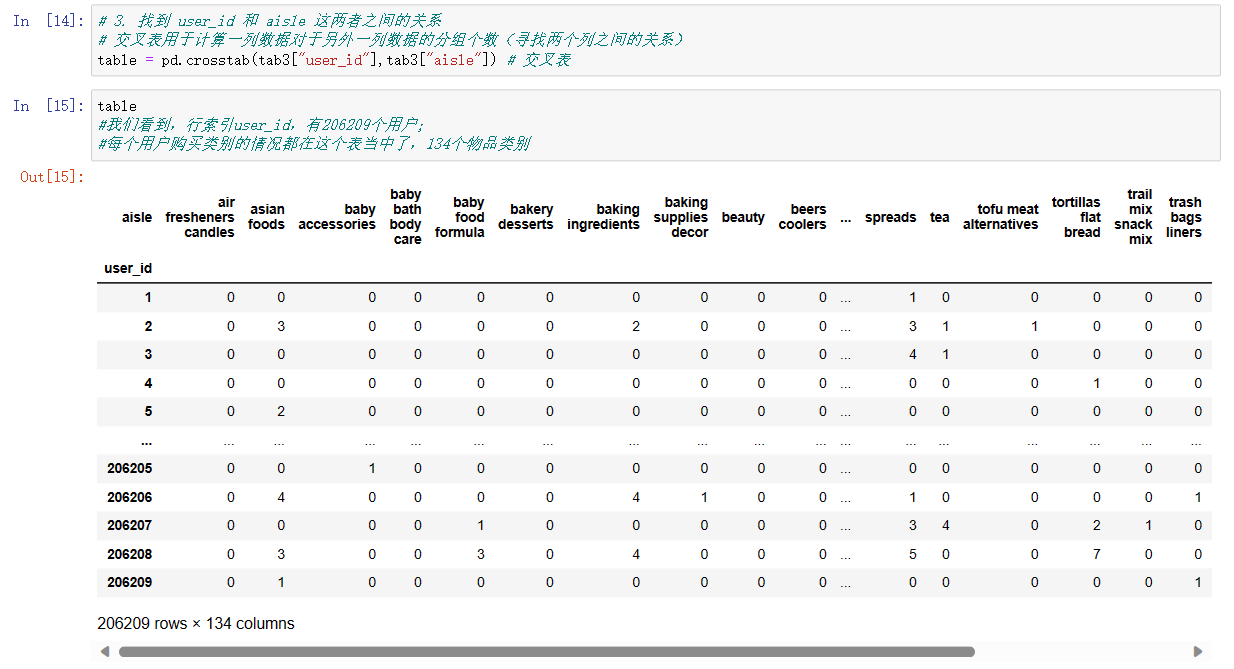
table = pd.crosstab(tab3["user_id"],tab3["aisle"]) # 交叉表
table
#我们看到,行索引user_id,有206209个用户;
#每个用户购买类别的情况都在这个表当中了,134个物品类别
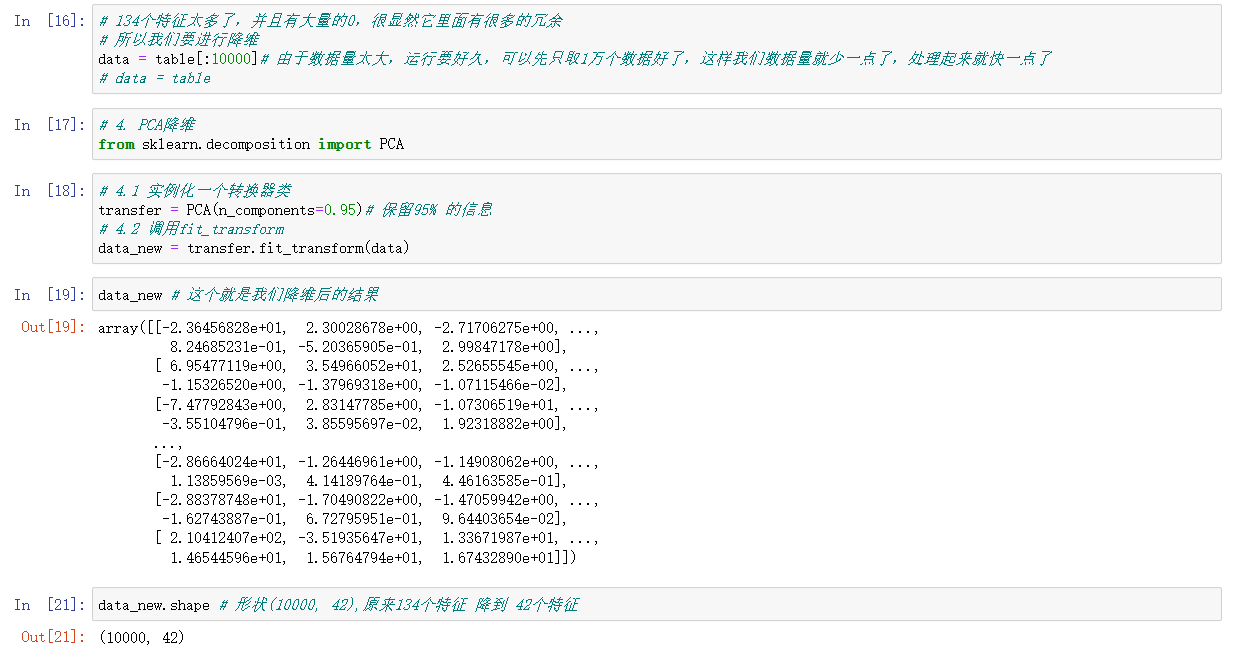
# 134个特征太多了,并且有大量的0,很显然它里面有很多的冗余
# 所以我们要进行降维
data = table[:10000]# 由于数据量太大,运行要好久,可以先只取1万个数据好了,这样我们数据量就少一点了,处理起来就快一点了
# data = table
# 4. PCA降维
from sklearn.decomposition import PCA
# 4.1 实例化一个转换器类
transfer = PCA(n_components=0.95)# 保留95% 的信息
# 4.2 调用fit_transform
data_new = transfer.fit_transform(data)
data_new # 这个就是我们降维后的结果
data_new.shape # 形状(10000, 42),原来134个特征 降到 42个特征
返回结果:
可以发现:其实我们在处理比较大一点的案例的时候,耗时比较多的是 数据处理 ,而真正用到机器学习相关的方法(特征工程)一两行就搞定了。
之后很大一部分工作都是在做数据处理。
总结
1、数据集的结构是什么?
答案: 特征值+ 目标值
2、机器学习算法分成哪些类别? 如何分类
答案: 根据是否有目标值分为 监督学习和非监督学习
根据目标值的数据类型: 目标值为离散值就是分类问题
目标值为连续值就是回归问题
3、什么是标准化? 和归一化相比有什么优点?
答案: 标准化是通过对原始数据进行变换把数据变换到均值为0,方差为1范围内
优点: 少量异常点, 不影响平均值和方差, 对转换影响小
分类算法
目标值:类别
1、sklearn转换器和预估器
2、KNN算法
3、模型选择与调优
4、朴素贝叶斯算法
5、决策树
6、随机森林
3.1 sklearn转换器和估计器
3.1.1 转换器和估计器
转换器
想一下之前做的特征工程的步骤?
- 1、实例化 (实例化的是一个转换器类(Transformer))
- 2、调用fit_transform(对于文档建立分类词频矩阵,不能同时调用)
标准化:
(x - mean) / std
fit_transform()
fit() 计算 每一列的平均值、标准差
transform() (x - mean) / std进行最终的转换
我们把特征工程的接口称之为转换器,其中转换器调用有这么几种形式
- fit_transform
- fit
- transform
这几个方法之间的区别是什么呢?我们看以下代码就清楚了
In [1]: from sklearn.preprocessing import StandardScaler
In [2]: std1 = StandardScaler()
In [3]: a = [[1,2,3], [4,5,6]]
In [4]: std1.fit_transform(a)
Out[4]:
array([[-1., -1., -1.],
[ 1., 1., 1.]])
In [5]: std2 = StandardScaler()
In [6]: std2.fit(a)
Out[6]: StandardScaler(copy=True, with_mean=True, with_std=True)
In [7]: std2.transform(a)
Out[7]:
array([[-1., -1., -1.],
[ 1., 1., 1.]])
从中可以看出,fit_transform的作用相当于transform加上fit。但是为什么还要提供单独的fit呢, 我们还是使用原来的std2来进行标准化看看
In [8]: b = [[7,8,9], [10, 11, 12]]
In [9]: std2.transform(b)
Out[9]:
array([[3., 3., 3.],
[5., 5., 5.]])
In [10]: std2.fit_transform(b)
Out[10]:
array([[-1., -1., -1.],
[ 1., 1., 1.]])
估计器(sklearn机器学习算法的实现)
在sklearn中,估计器(estimator)是一个重要的角色,是一类实现了算法的API
- 用于分类的估计器:
- sklearn.neighbors k-近邻算法
- sklearn.naive_bayes 贝叶斯
- sklearn.linear_model.LogisticRegression 逻辑回归
- sklearn.tree 决策树与随机森林
- 用于回归的估计器:
- sklearn.linear_model.LinearRegression 线性回归
- sklearn.linear_model.Ridge 岭回归
- 用于无监督学习的估计器
- sklearn.cluster.KMeans 聚类
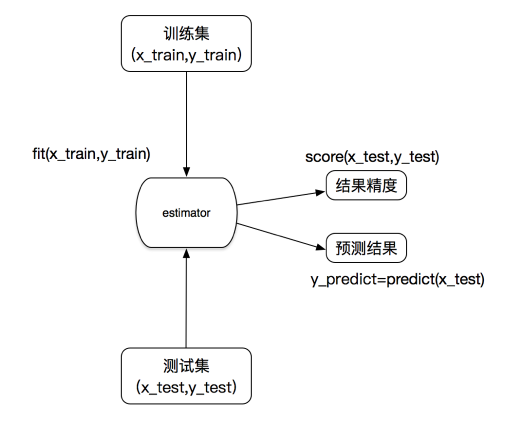
估计器工作流程
回忆本博客 2.1.3 数据集的划分
| 数据集的划分 | 取名 |
|---|---|
| 训练集特征值 | x_train |
| 测试集特征值 | x_test |
| 训练集目标值 | y_train |
| 测试集目标值 | y_test |
估计器(estimator)
1 实例化一个estimator
2 estimator.fit(x_train, y_train) 计算
—— 调用完毕,模型生成
3 模型评估:
1)直接比对真实值和预测值
y_predict = estimator.predict(x_test)
y_test == y_predict
2)计算准确率
accuracy = estimator.score(x_test, y_test)
3.2 K-近邻算法
问题:回忆分类问题的判定方法
什么是K-近邻算法
核心思想:你的“邻居”来推断出你的类别
K-近邻算法是怎么进行分类的?下面我们通过例子来讲解基本原理
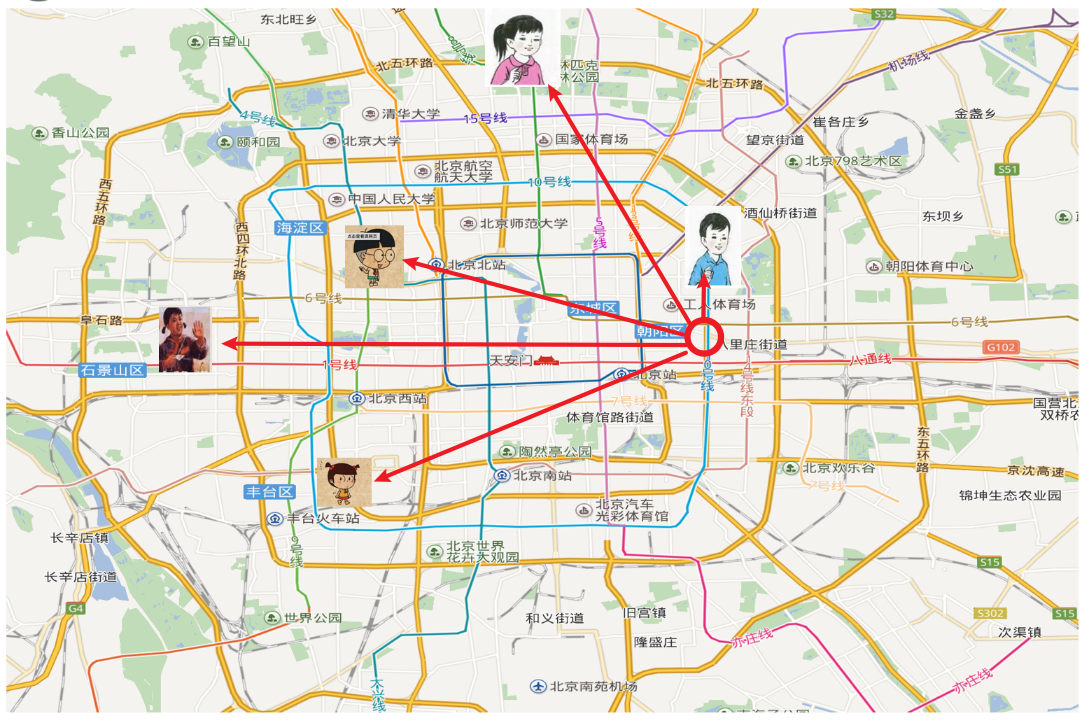
假如说我在这个圆圈的位置,我不知道我在北京的哪个区,我想要知道我现在在北京哪个区,这个可以看成分类问题,我想要解决这个分类问题,如果我用K近邻算法的话就是这样的一个思路,我虽然不知道我在哪,但是我知道我跟这几个人之间的距离,并且我也知道这五个人在哪个区,想要去判断我到底属于哪个区 我是不是可以看最近的人在哪个区 我就有极大的可能性就在哪个区,所以我们就看到我们跟蓝色的小男孩这个距离最近的,而他在朝阳区,所以我就判断我所在的区域就是在北京的朝阳区。这就是K-近邻算法的原理,就这么简单。
1、K-近邻算法(KNN)原理
K Nearest Neighbor算法又叫KNN算法,这个算法是机器学习里面一个比较经典的算法, 总体来说KNN算法是相对比较容易理解的算法。
一句话:根据我的邻居来判断我的类别
1.1 定义
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
注意:
如果k=1,k值取很小,容易受到异常点的影响。
k值取很大,受到样本均衡的问题,容易受到样本不均衡的影响。
来源:KNN算法最早是由Cover和Hart提出的一种分类算法
1.2 距离公式
两个样本的距离可以通过如下公式计算,又叫欧式距离。
扩展:
- 除了欧氏距离可以衡量以外,还有一个叫做 曼哈顿距离(绝对值距离)
=|a1-b1|+|a2-b2|+|a3-b3| 绝对值- 闵可夫斯基距离 (Minkowski Distance),也被称为 闵氏距离。它不仅仅是一种距离,而是将多个距离公式(曼哈顿距离、欧式距离、切比雪夫距离)总结成为的一个公式。
曼哈顿距离、欧式距离是闵可夫斯基距离的特殊情况。我们说 闵可夫斯基距离 是 曼哈顿距离、欧式距离的一个推广。
2、电影类型分析
| 电影名称 | 打斗镜头 | 接吻镜头 | 电影类型 |
|---|---|---|---|
| California Man | 3 | 104 | 爱情片 |
| He’s not Really into dues | 2 | 100 | 爱情片 |
| Beautiful Woman | 1 | 81 | 爱情片 |
| Kevin Longblade | 101 | 10 | 动作片 |
| Robo Slayer 3000 | 99 | 5 | 动作片 |
| Amped Il | 98 | 2 | 动作片 |
? | 18 | 90 | 未知 |
其中 ? 号电影不知道类别,如何去预测?我们可以利用K近邻算法的思想
| 电影名称 | 与未知电影的距离 |
|---|---|
| California Man | 20.5 |
| He’s not Really into dues | 18.7 |
| Beautiful Woman | 19.2 |
| Kevin Longblade | 115.3 |
| Robo Slayer 3000 | 117.4 |
| Amped Il | 118.9 |
假如说k取了1,那么也就是说离我最近的就是 He’s not Really into dues ,距离18.7,而他是属于爱情片,所以我们就认为 未知电影 属于爱情片。
......
k=6, 意味着我们需要取离我们样本最近的6个,找到其中的大多数的类别作为我们最终的类别,但是现在我们看到我们总共就6个样本,而且6个样本有一半是爱情片,一半是动作片,我们没有办法找到它属于哪个类别。无法确定
假设我在我的 样本(训练集) 当中, 再加一个电影,特征什么的先不管他,我们随便给他一个特征, 不管他什么特征,最后类别让他是动作片,会出现什么样的影响?
| 电影名称 | 打斗镜头 | 接吻镜头 | 电影类型 |
|---|---|---|---|
| California Man | 3 | 104 | 爱情片 |
| He’s not Really into dues | 2 | 100 | 爱情片 |
| Beautiful Woman | 1 | 81 | 爱情片 |
| Kevin Longblade | 101 | 10 | 动作片 |
| Robo Slayer 3000 | 99 | 5 | 动作片 |
| Amped Il | 98 | 2 | 动作片 |
| 加的电影 | 90 | 1 | 动作片 |
? | 18 | 90 | 未知 |
k=7, 离我 未知电影 最近的7个样本当中,有3个是爱情片,有4个是动作片,导致最终分成了动作片,但是我们看我们 未知电影 的接吻镜头 远远大于 打斗镜头的,那么它很有可能就是爱情片,所以也就意味着 当我们k值取得过大,当样本不均衡的时候,容易受到样本不均衡的影响(分错)。
2.1 问题
-
如果取的最近的电影数量不一样?会是什么结果?
回答: k 值取得过小,容易受到异常点的影响;k 值取得过大,样本不均衡的影响。 -
结合前面的约会对象数据,分析K-近邻算法需要做什么样的处理?
无量纲化的处理
标准化
2.2 K-近邻算法API
- sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)
Neighbors 邻居
Classifier 分类器- n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数。其实就是K近邻中的 k值 。
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法:‘ball_tree’将会使用 BallTree,‘kd_tree’将使用 KDTree。‘auto’ 将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)
这个算法其实跟机器学习算法没有什么关系,它只是说我们在计算样本之间的距离的时候, 你需要找到你的邻居,那么它就需要进行 搜索排序查询 这其实是 数据结构层面 的东西。这个你就不用管它,它本来就实现的挺好的,按默认的 ‘auto’ ,它就会根据你fit进来的特征值和目标值 选择最合适的算法进行计算,会选择效率最高的方法。
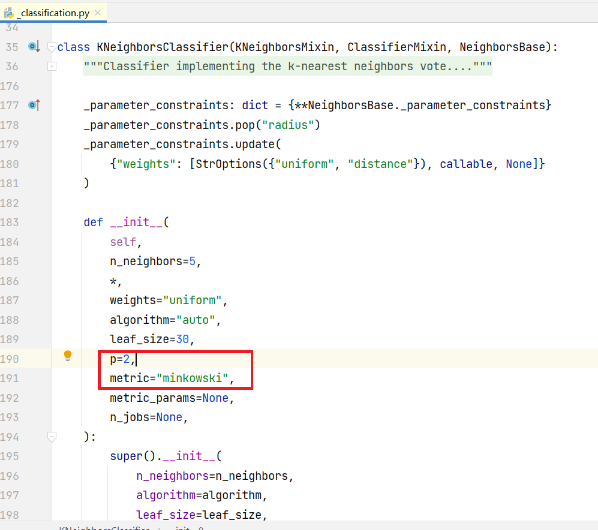
- 我们在调用KNeighborsClassifier的时候如何去体现这个距离?其实就是这些参数
- metric=“minkowski”
"minkowski"其实就是 闵可夫斯基距离 的意思,但是我们在经常在使用的时候是用的 欧氏距离 ,看参数 p - p=2 默认欧氏距离
我们说 闵可夫斯基距离 是 曼哈顿距离、欧式距离的一个推广,闵可夫斯基距离 当中 公式 里面 有一个p值。如果 p值=1 的话,就是 曼哈顿距离(绝对值距离) ;p值=2 那就是 欧氏距离。
- metric=“minkowski”
3、案例:鸢尾花种类预测
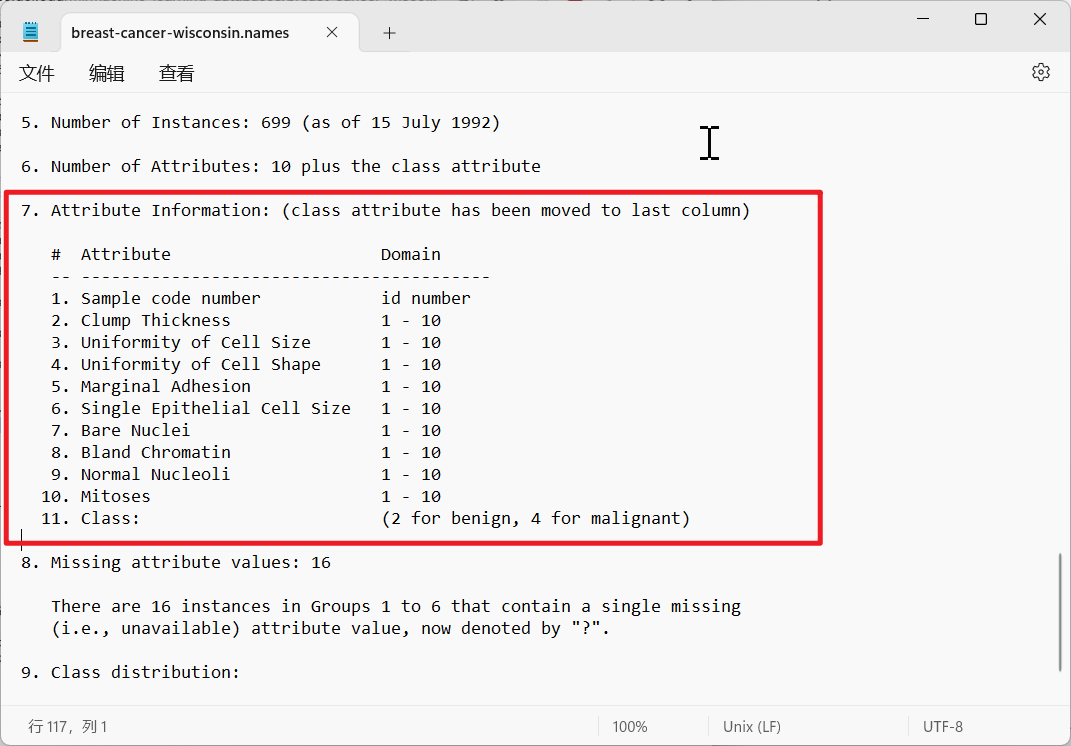
数据集介绍
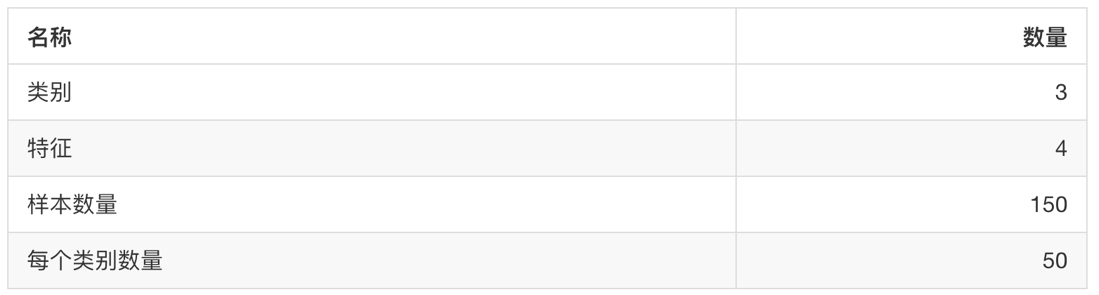
lris数据集是常用的分类实验数据集,由Fisher,1936收集整理。lris也称鸢尾花卉数据集,是一类多重变量分析的数据集。关于数据集的具体介绍:
实例数量: 150(三个类各有50个)
属性数量: 4(数值型,数值型,帮助预测的属性和类)
Attribute Information:
- sepal length 萼片长度 (厘米)
- sepal width 萼片宽度 (厘米)
- petal length 花瓣长度 (厘米)
- petal width 花瓣宽度 (厘米)
- class:
- Iris-Setosa 山鸢尾
- lris-Versicolour 变色尾
- lris-Virginica 维吉尼亚鸢尾
步骤分析
- 获取数据
- 数据集划分
- 特征工程:标准化
- KNN预估器流程
- 模型评估
代码
KNN算法对鸢尾花进行分类
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
def knn_iris():
"""
KNN算法对鸢尾花进行分类
:return:
"""
# 1.获取数据
iris = load_iris()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
# 参数: test_size 测试集的大小 默认0.25
# random_state 随机数种子
# 3.特征工程: 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train) # 训练集做了标准化
x_test = transfer.transform(x_test) # 测试集也需要做标准化
# 4.KNN预估器流程
estimator = KNeighborsClassifier(n_neighbors=3)
estimator.fit(x_train, y_train) # 得到模型
# 5.模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n",y_test==y_predict)
# 方法二: 计算准确率
score=estimator.score(x_test,y_test)
print("准确率为:\n",score)
return None
if __name__ == "__main__":
knn_iris()
分析代码 3. 特征工程:标准化
因为你其实相当于 让模型最终用同样分布的 分布状况的 数据 来对这个模型进行检验。所以训练集做了什么手脚,那么测试集也必须要做同样的手脚,这样才能真正的检验出来他到底好不好。
在进行标准化的时候,是分两步的
1.fit 计算 - 每一列的平均值、标准差
2.transform 转换
如果我要对测试集也要进行标准化,那么这时候用fit_transform还是用transform?
测试集 应该用transform
transfer.fit_transform(x_train) 相当于对训练集每个特征求了一个平均值和标准差, 然后在进行最终的标准化的时候, 用的训练集的平均值和标准差进行 转换, 如果你在调用 x_test 测试集进行标准化的话, 如果你用的是测试集的平均值标准差, 那相当于对测试集做了不一样的处理。我们希望的是对测试集做跟训练集一样的处理, 所以我们就需要用 训练集 特征当中的标准差和平均值来对测试集的数据进行标准化。所以这个时候, 我们在对测试集进行标准化, 要用transform不要用fit_transform。
运行结果
y_predict:
[0 2 0 0 2 1 1 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
2]
直接比对真实值和预测值:
[ True True True True True True False True True True True True
True True True False True True True True True True True True
True True True True True True True True True True False True
True True]
准确率为:
0.9210526315789473
数据集划分不一样可能结果就不一样
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
结果:
y_predict:
[0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True True True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True]
准确率为:
0.9736842105263158
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=23)
结果:
y_predict:
[2 2 1 0 2 1 0 2 0 1 1 0 2 0 0 2 1 1 2 0 2 0 0 0 2 0 0 2 1 1 0 1 0 2 0 0 1
1]
直接比对真实值和预测值:
[ True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True]
准确率为:
1.0
结果分析
- k值取多大? 有什么影响?
- k值取很小:容易受到异常点的影响
- k值取很大:受到样本均衡的问题
- 性能问题?
- 距离计算上面,时间复杂度高
所以在大数据场景下效率比较低
- 距离计算上面,时间复杂度高
4、K-近邻总结
- 优点:
- 简单,易于理解,易于实现,无需训练
- 缺点:
- 必须指定K值,K值选择不当则分类精度不能保证
- 属于懒惰算法,对测试样本分类时的计算量大,内存开销大。
- 使用场景: 一般适合
小数据场景,几千~几万样本,具体场景具体业务去测试
KNN算法他有一个缺陷,其中一个缺陷就是这个k值取值是不一定的,我们需要选择一个合适的k值取得尽可能好的结果。有没有一个方法能够方便的让我们去选择最合适的k值呢? 模型选择与调优 这部分 是可以解决这个问题的。
3.3 模型选择与调优
1、为什么需要交叉验证
交叉验证目的:为了让被评估的模型更加准确可信
2、什么是交叉验证(cross validation)
交叉验证:将拿到的训练数据,分为训练和验证集。以下图为例:将数据分成5份,其中一份作为验证集。然后经过 4或者5 次(组)的测试,每次都更换不同的验证集。即得到 4或者5组模型的结果(准确率),取平均值作为最终结果。又称4折交叉验证 或者 5折交叉验证。
2.1 分析
我们之前知道数据分为训练集和测试集,但是为了让从训练得到模型结果更加准确。做以下处理
- 训练集:训练集+验证集
- 测试集:测试集
问题:那么这个只是对于参数得出更好的结果,那么怎么选择或者调优参数呢?
3、超参数搜索-网格搜索(Grid Search)
举个例子,我们要对k值进行选择,我们如何选择合适的k值,我们最能想到的、最简单的方法就是 准备一些k值[1, 3, 5, 7, 9, 11],我想知道这里面哪个参数能让我们最后分类效果是最好的,能够得到最高的准确率。我们最先想到的是怎么得出这个结论呀?是不是就是遍历,就跟密码暴力破解似的,一个一个试一下,写个for循环一个一个试,其实网格搜索就是在帮助我们自动做这些事情,只不过我们不需要自己去写这个for循环了。
通常情况下,有很多参数是需要手动指定的(如k-近邻算法中的K值),这种叫超参数。但是手动过程繁杂,所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
| K值 | K=3 | K=5 | K=7 |
|---|---|---|---|
| 模型 | 模型1 | 模型2 | 模型3 |
3.1 模型选择与调优API
- sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
Grid 网格 Search 搜索
CV 交叉验证 cross validation- 对估计器的指定参数值进行详尽搜索
- estimator:估计器对象
我们用的时候GridSearchCV也相当于一个继承自estimator预估器的一个类,所以我们使用的时候跟预估器的使用方法是一样的。.fit() 和 .score() - param_grid:估计器参数(dict) {“n_neighbors”:[1,3,5]}
- cv:指定几折交叉验证
最常用的就是10折交叉验证,如果数据量比较大的话,单纯演示的话,10折会很耗时,可以设置小一点。 - fit():输入训练数据
- score():准确率
- 属性
- 结果分析:
- 最佳参数: best_params_
- 最佳结果: best_score_
在交叉验证中验证的最好结果 - 最佳估计器: best_estimator_
最好的参数模型 - 交叉验证结果: cv_results_
每次交叉验证后的验证集准确率结果和训练集准确率结果
- 结果分析:
4、鸢尾花案例增加K值调优
拿上一个案例的代码,在这基础上增加K值调优
- 使用GridSearchCV构建估计器
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
def knn_iris_gscv():
"""
KNN算法对鸢尾花进行分类, 添加网格搜索和交叉验证
:return:
"""
# 1.获取数据
iris = load_iris()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 参数: test_size 测试集的大小 默认0.25
# random_state 随机数种子
# 3.特征工程: 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train) # 训练集做了标准化
x_test = transfer.transform(x_test) # 测试集也需要做标准化
# 4.KNN预估器流程
# estimator = KNeighborsClassifier(n_neighbors=3)
estimator = KNeighborsClassifier() # 没必要加上k值了
# 添加网格搜索和交叉验证
param_dict = {'n_neighbors': [1, 3, 5, 7, 9, 11]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)
# 本身数据量不大,只有150个样本, 10折交叉验证, 还用estimator接收,这样后面的代码就不用改了
estimator.fit(x_train, y_train) # 得到模型
# 5.模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法二: 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
print("+" * 10 + "分隔线" + "+" * 10)
print('最佳参数:\n', estimator.best_params_)
print('最佳结果:\n', estimator.best_score_)
print('最佳估计器:\n', estimator.best_estimator_)
print('交叉验证结果:\n', estimator.cv_results_)
return None
if __name__ == "__main__":
knn_iris_gscv()
y_predict:
[0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True True True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True]
准确率为:
0.9736842105263158
++++++++++分隔线++++++++++
最佳参数:
{'n_neighbors': 3}
最佳结果:
0.9553030303030303
最佳估计器:
KNeighborsClassifier(n_neighbors=3)
交叉验证结果:
{'mean_fit_time': array([0.00138659, 0. , 0.00150073, 0.00156238, 0. ,
0.00010364]), 'std_fit_time': array([0.00374409, 0. , 0.00450218, 0.00468714, 0. ,
0.00031092]), 'mean_score_time': array([0.00169234, 0.00156777, 0.00156312, 0. , 0.00316582,
0.00312572]), 'std_score_time': array([0.0033536 , 0.00470331, 0.00468936, 0. , 0.00526248,
0.00625143]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],
mask=[False, False, False, False, False, False],
fill_value='?',
dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([0.91666667, 0.91666667, 1. , 1. , 0.91666667,
0.91666667]), 'split1_test_score': array([1., 1., 1., 1., 1., 1.]), 'split2_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.90909091]), 'split3_test_score': array([0.90909091, 1. , 0.90909091, 0.90909091, 0.90909091,
1. ]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.90909091]), 'split6_test_score': array([0.90909091, 0.90909091, 0.90909091, 1. , 1. ,
1. ]), 'split7_test_score': array([0.90909091, 0.90909091, 0.81818182, 0.81818182, 0.81818182,
0.81818182]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([1., 1., 1., 1., 1., 1.]), 'mean_test_score': array([0.94621212, 0.95530303, 0.94545455, 0.95454545, 0.94621212,
0.95530303]), 'std_test_score': array([0.04397204, 0.0447483 , 0.06030227, 0.06098367, 0.05988683,
0.0604591 ]), 'rank_test_score': array([4, 1, 6, 3, 4, 1])}
首先,预测值y_predict 虽然用的不再是之前的estimator,我们用的是GridSearchCV,但是它一样也是可以得出结果的。
然后就是比对真实值和预测值 准确率 0.97,模型选择与调优的最佳结果 准确率 0.95 ,为什么准确率和最佳结果会不一样 ?注意,best_score_,这个属性会存储模型在交叉验证中所得的最高分,而不是测试数据集上的得分。<\b>
5、案例:预测facebook签到位置
facebook发布在kaggle上的一个比赛
数据介绍:将根据用户的位置,准确性和时间戳预测用户正在查看的业务。
train.csv,test.csv
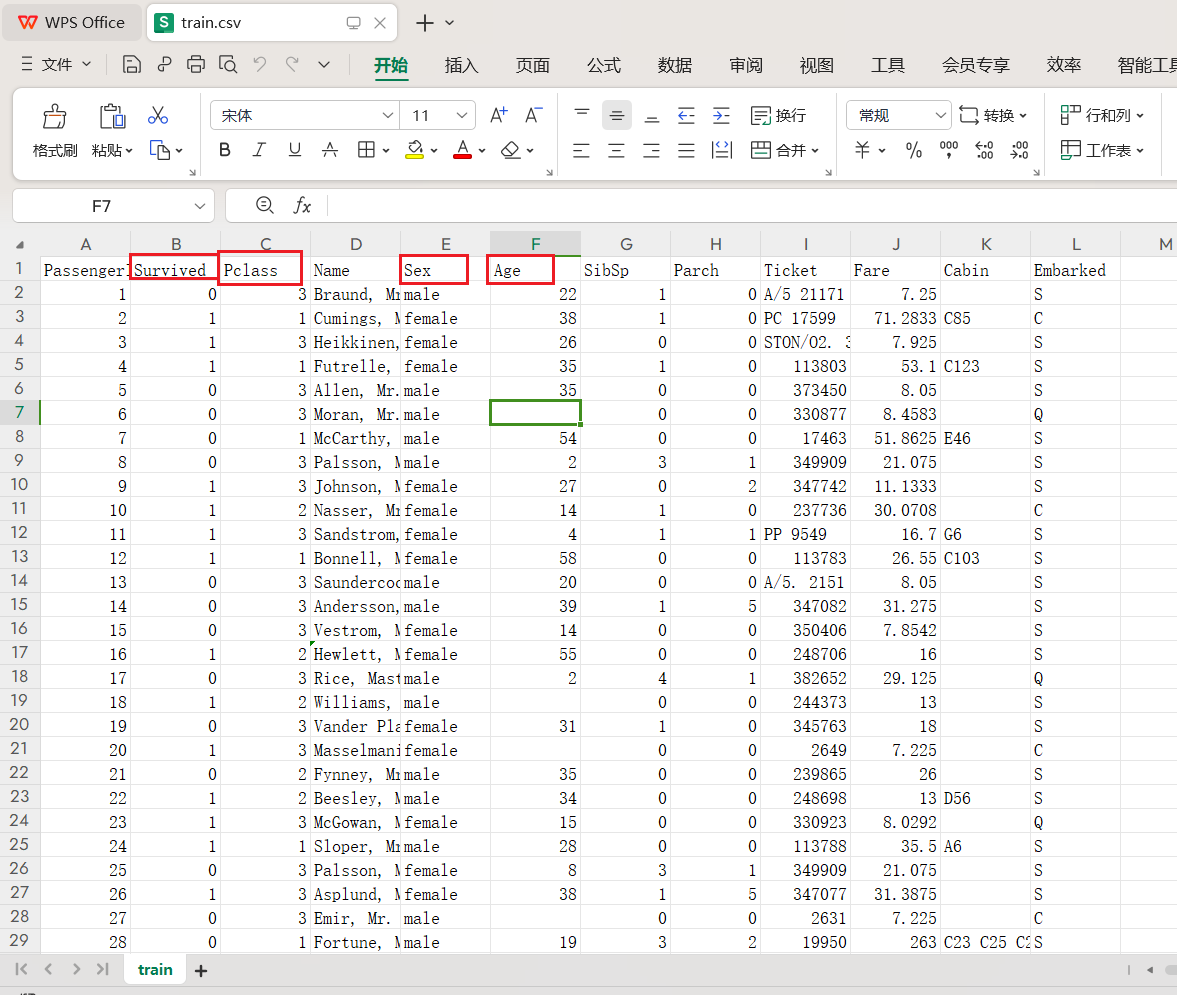
row_id:登记事件的ID。签到行为的编码,其实就相当于一个索引,没什么意义。
x y:坐标。x y 其实就是坐标系,就是人所在的位置。
accuracy 准确性:定位准确性 。我们一般是用手机上的GPS定位,但是这个定位也可能不太准,因为不同的卫星它的准确度是不一样的,这是他的一个字段,代表定位的准确度、准确率。
time 时间:时间戳 。1970-01-01 到 某一天的秒数。
place_id:业务的ID,这是您预测的目标。预测我们用户将要签到的位置是什么。
文件我放网盘里了 链接:https://pan.baidu.com/s/1XFWGZJopEeZGw3gIbGQeTg?pwd=1024
提取码:1024
FBlocation 文件夹,train.csv、test.csv
我们看到train.csv文件1.18G是很大的, 所以我们在梳理数据的时候,如果我们要反复的调试这些数据,如果用PyCharm每次运行要重新加载一遍,非常的麻烦,所以我们还是用jupyter
流程分析
1)获取数据
2)数据处理
目的:
特征值
目标值
a. 缩小数据范围(练习的时候才会这么做,为了节省时间),缩小数据范围跟真实开发情况中不需要去做的这个事,我们本身数据量太大了,2千多万条数据如果我们所有的数据都一并处理的话,比较耗时。
比如说我们按坐标,以xy坐标为基准进行缩小,总共是10万 x 10万这样的一块区域,我们给它取一小块作为我们数据集进行进一步的分析,那么就可以根据坐标来缩小范围,比如说我取坐标在
2 < x <2.5
1.0 < y < 1.5 看你自己想怎么取怎么取
b. time 一> 年月日时分秒。 time字段只是一个时间戳,但是作为特征来讲,我们希望这个时间更有意义,比如说早上,如果你去预测你签了一次到,很有可能是在公园或者在通勤的路上,这些都有可能;或者说在周六很可能就在商场,可能在家睡觉这些都是有可能的。所以我们如果用时间这个特征的话,我们更希望这个事件不是单一的时间戳,而是更有意义的年月日时分秒…
c. 过滤签到次数少的地点其实我们这么多签到的数据,里面签到的地点,很有可能有些地点最多只被签到了一次或者两次,对于 这种地点对于facebook没有统计意义,我们更希望知道经常去的地点,它的一个情况。所以我们在数据处理的时候,也可以签到地点 签到次数比较少的地方直接排除掉。
3)特征工程:标准化
4)KNN算法预估流程
5)模型选择与调优
6)模型评估
代码
import pandas as pd
# 1.. 获取数据
data = pd.read_csv("./FBlocation/train.csv")
data
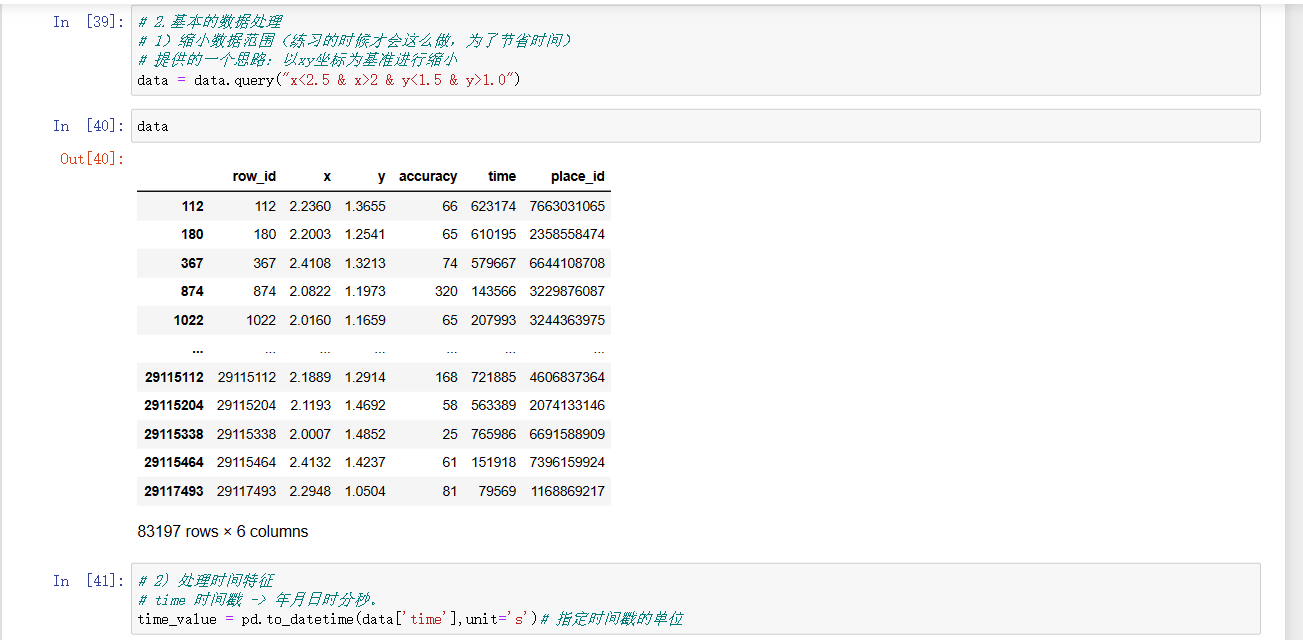
# 2.基本的数据处理
# 1)缩小数据范围(练习的时候才会这么做,为了节省时间)
# 提供的一个思路:以xy坐标为基准进行缩小
data = data.query("x<2.5 & x>2 & y<1.5 & y>1.0")
data
# 2) 处理时间特征
# time 时间戳 -> 年月日时分秒。
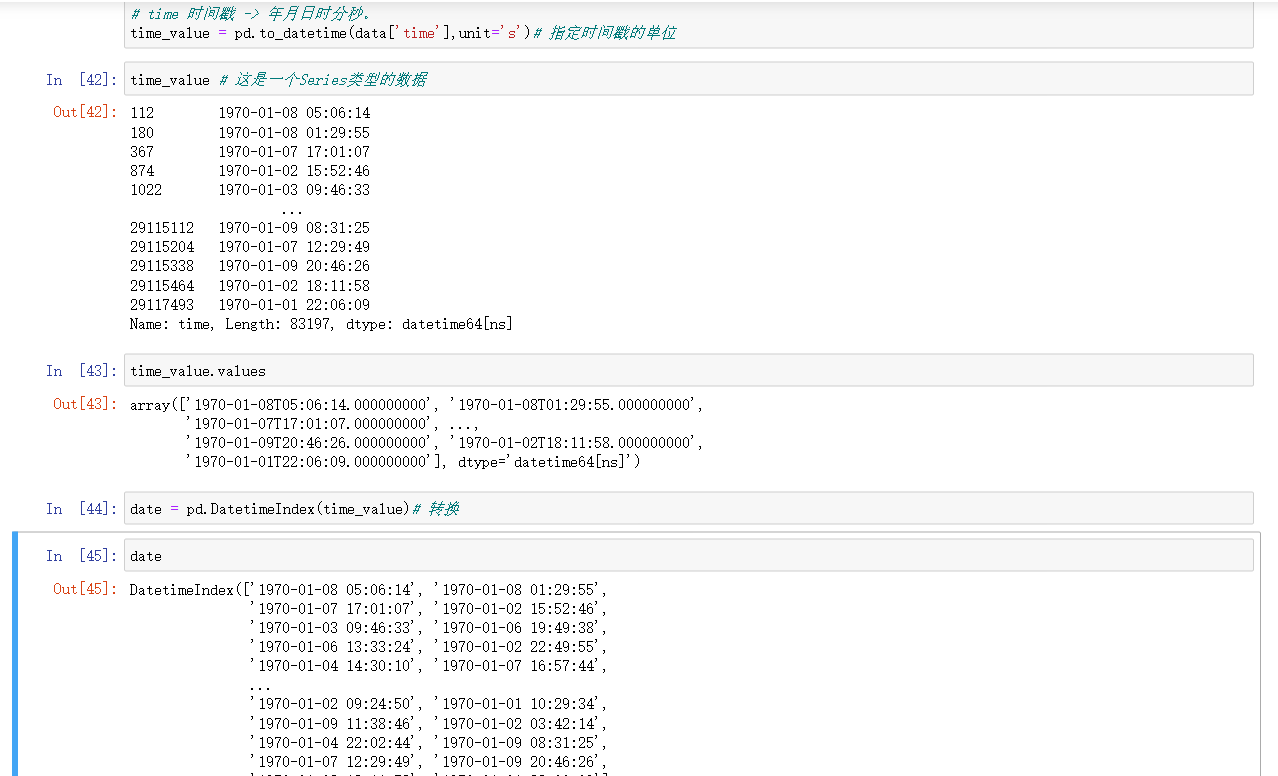
time_value = pd.to_datetime(data['time'],unit='s')# 指定时间戳的单位
time_value # 这是一个Series类型的数据
time_value.values
date = pd.DatetimeIndex(time_value)# 转换
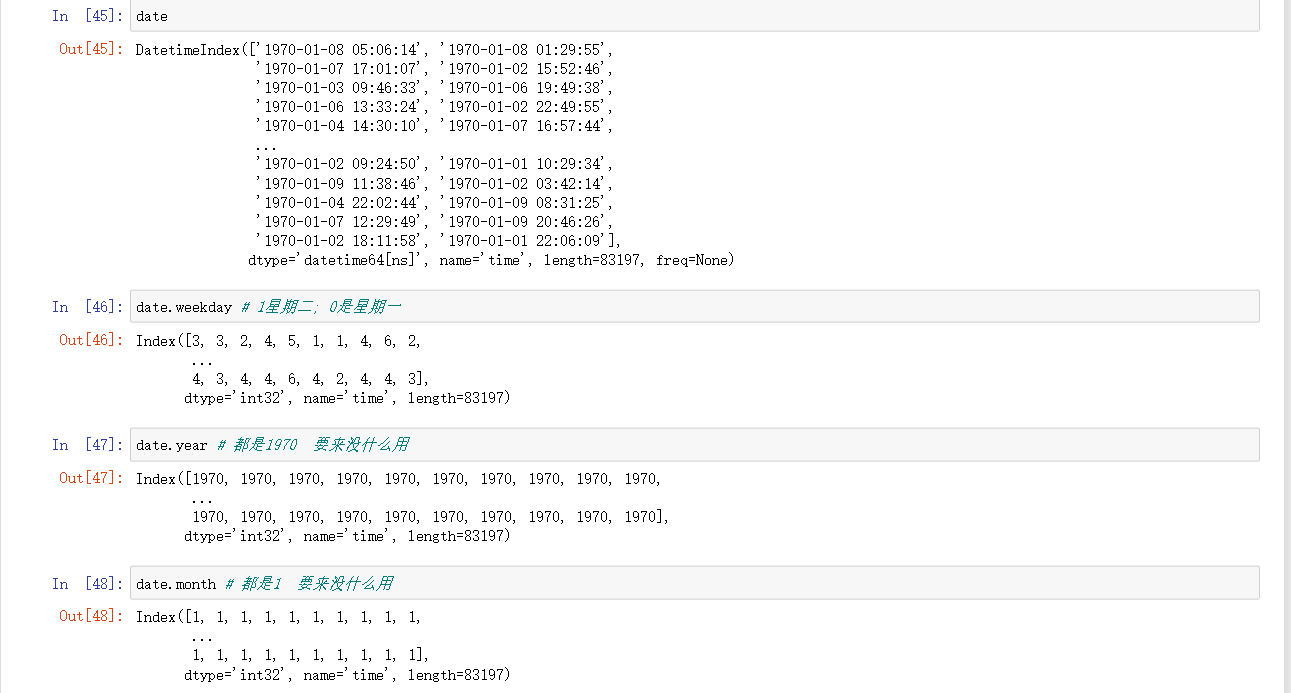
date
date.weekday # 1星期二; 0是星期一
date.year # 都是1970 要来没什么用
date.month # 都是1 要来没什么用
date.day # 日期
date.hour # 小时
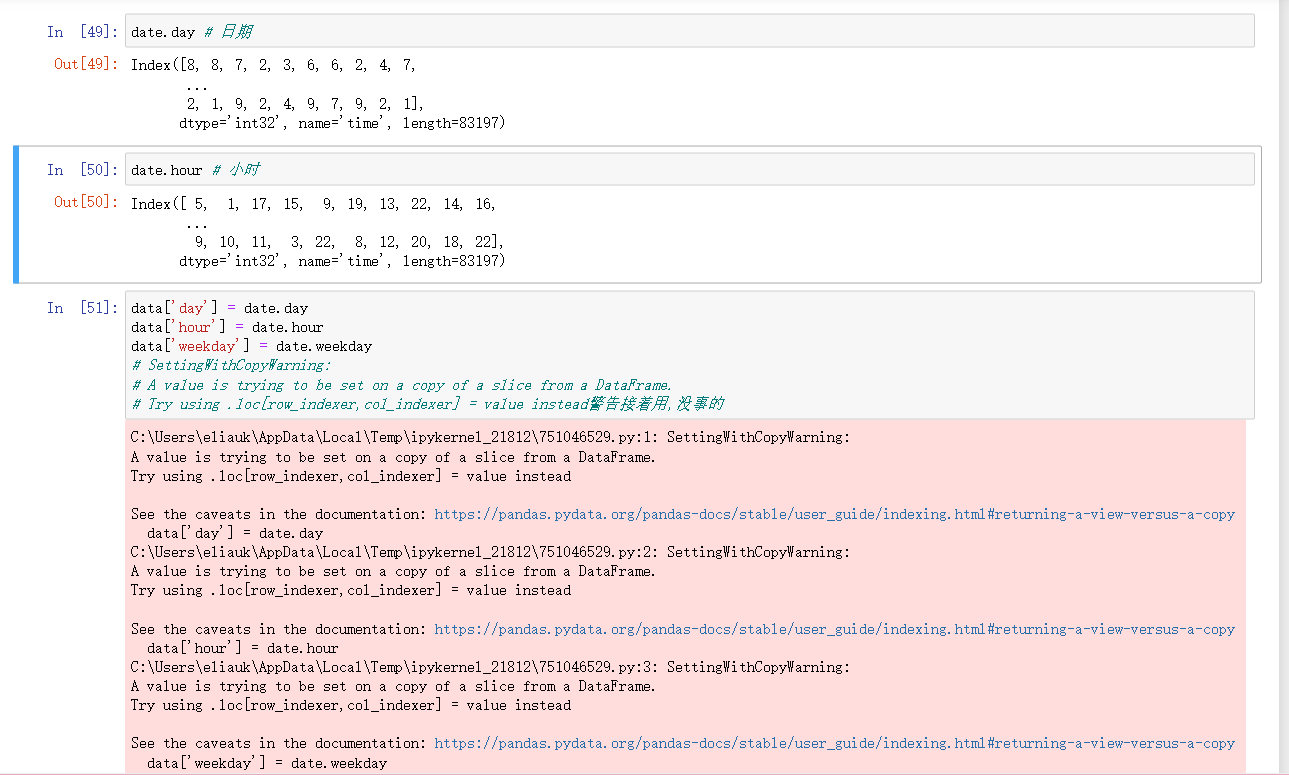
data['day'] = date.day
data['hour'] = date.hour
data['weekday'] = date.weekday
# SettingWithCopyWarning:
# A value is trying to be set on a copy of a slice from a DataFrame.
# Try using .loc[row_indexer,col_indexer] = value instead警告接着用,没事的
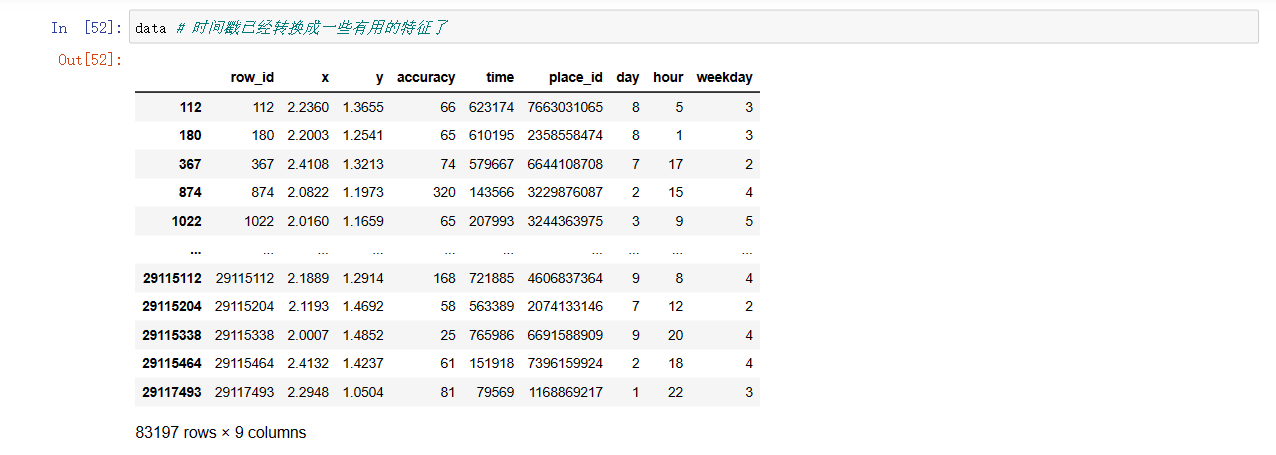
data # 时间戳已经转换成一些有用的特征了
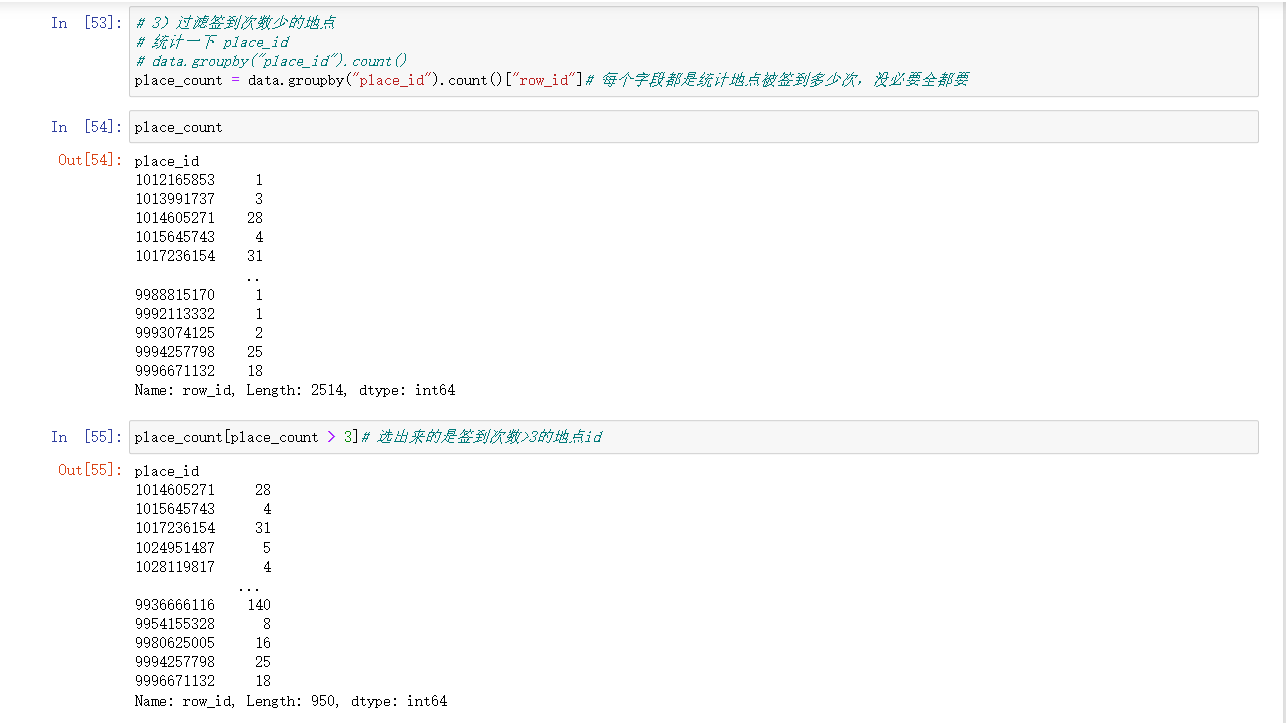
# 3)过滤签到次数少的地点
# 统计一下 place_id
# data.groupby("place_id").count()
place_count = data.groupby("place_id").count()["row_id"]# 每个字段都是统计地点被签到多少次,没必要全都要
place_count
place_count[place_count > 3]# 选出来的是签到次数>3的地点id
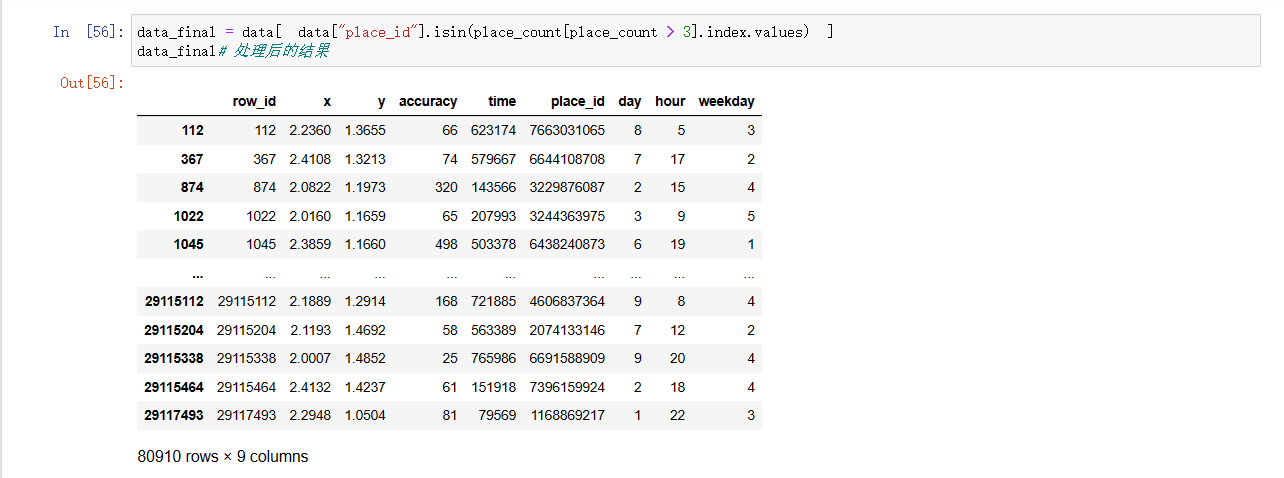
data_final = data[ data["place_id"].isin(place_count[place_count > 3].index.values) ]
data_final# 处理后的结果
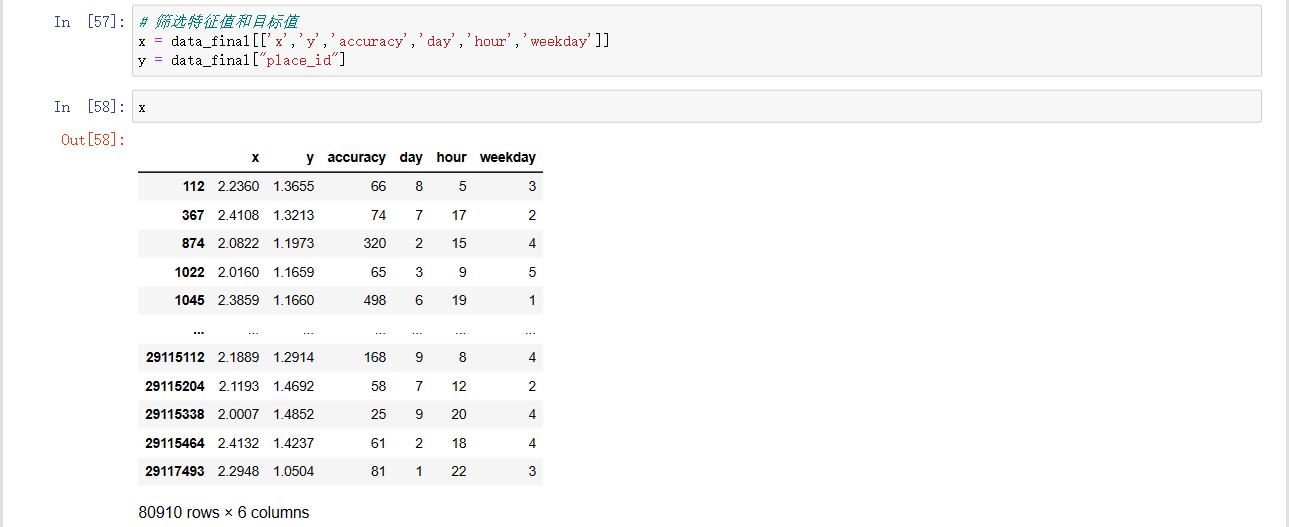
# 筛选特征值和目标值
x = data_final[['x','y','accuracy','day','hour','weekday']]
y = data_final["place_id"]
x
y
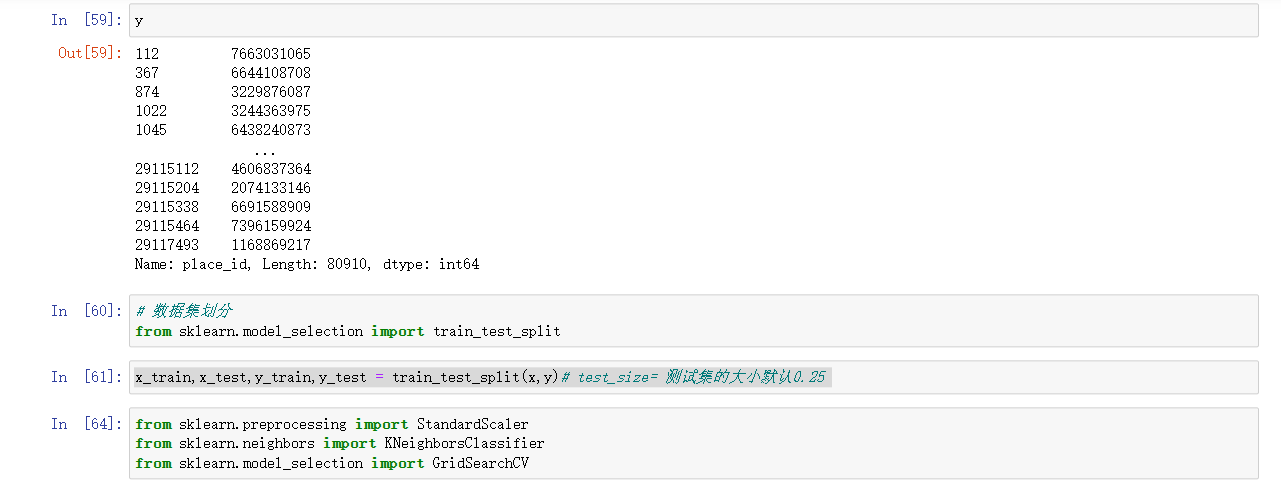
# 数据集划分
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y)# test_size= 测试集的大小默认0.25
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# 3.特征工程: 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train) # 训练集做了标准化
x_test = transfer.transform(x_test) # 测试集也需要做标准化
# 4.KNN预估器流程
estimator = KNeighborsClassifier()
# 添加网格搜索和交叉验证
param_dict = {'n_neighbors': [ 3, 5, 7, 9, 11]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10) # 10折交叉验证,数据量大建议用cv=3
estimator.fit(x_train, y_train) # 得到模型
# 5.模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法二: 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
print("+" * 10 + "分隔线" + "+" * 10)
print('最佳参数:\n', estimator.best_params_)
print('最佳结果:\n', estimator.best_score_)
print('最佳估计器:\n', estimator.best_estimator_)
print('交叉验证结果:\n', estimator.cv_results_)
运行结果
y_predict:
[5304570159 1949544719 5232128865 ... 5448001036 5232128865 6787040850]
直接比对真实值和预测值:
28017380 False
8859899 False
9587364 False
2067248 True
15917174 False
...
4937248 False
23673105 False
27174947 True
13917941 True
28518400 False
Name: place_id, Length: 20228, dtype: bool
准确率为:
0.3606387186078703
++++++++++分隔线++++++++++
最佳参数:
{'n_neighbors': 5}
最佳结果:
0.3597607708017869
最佳估计器:
KNeighborsClassifier()
交叉验证结果:
{'mean_fit_time': array([0.08854768, 0.10602798, 0.18479028, 0.11244125, 0.10711095]), 'std_fit_time': array([0.0144927 , 0.0233614 , 0.06470464, 0.0105941 , 0.0051431 ]), 'mean_score_time': array([0.38352401, 0.55316637, 1.04415717, 0.58939171, 0.58459861]), 'std_score_time': array([0.05664922, 0.16247061, 0.36381429, 0.04717116, 0.0345666 ]), 'param_n_neighbors': masked_array(data=[3, 5, 7, 9, 11],
mask=[False, False, False, False, False],
fill_value='?',
dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([0.3504696 , 0.3592025 , 0.3592025 , 0.35854342, 0.35376504]), 'split1_test_score': array([0.34453782, 0.35722524, 0.35475367, 0.35425935, 0.35096391]), 'split2_test_score': array([0.34574819, 0.35332894, 0.35431773, 0.35332894, 0.34640738]), 'split3_test_score': array([0.33487146, 0.35613052, 0.35102175, 0.34739618, 0.3436058 ]), 'split4_test_score': array([0.33635465, 0.35596572, 0.35629532, 0.34871457, 0.34459459]), 'split5_test_score': array([0.3590969 , 0.36931444, 0.36783125, 0.35711931, 0.35266974]), 'split6_test_score': array([0.34228741, 0.36189848, 0.36618326, 0.3600857 , 0.35135135]), 'split7_test_score': array([0.34920897, 0.36404087, 0.36189848, 0.35711931, 0.35580092]), 'split8_test_score': array([0.35530653, 0.36255768, 0.35843771, 0.35497693, 0.35266974]), 'split9_test_score': array([0.34772577, 0.35794331, 0.36420567, 0.3600857 , 0.35810811]), 'mean_test_score': array([0.34656073, 0.35976077, 0.35941473, 0.35516294, 0.35099366]), 'std_test_score': array([0.0072188 , 0.00448305, 0.00524071, 0.00416735, 0.00451348]), 'rank_test_score': array([5, 1, 2, 3, 4])}
我们看到有很多错的,因为我们用的数据也是比较少的,我们取了8万多条数据,数据量也不是特别够,最后准确率才30%多。但是这个过程是没有问题的。自己做的时候可以多加一些数据处理,特征工程也可以发挥自己创意 的处理。这里就不拓展了,知道流程就行。
我们可以发现花费时间最多的地方是数据处理,其他的都是别的案例复制过来的
- date.year
- date.month
- date.weekday 1星期二; 0是星期一
pandas.to_datetime(arg, errors=‘raise’, dayfirst=False, yearfirst=False, utc=None, format=None, exact=True, unit=None, infer_datetime_format=False, origin=‘unix’, cache=True
- errors:参数raise时,表示传入数据格式不符合是会报错;ignore时,表示忽略报错返回原数据;coerce用NaT时间空值代替。
- dayfirst:表示传入数据的前两位数为天。如‘030820’——>2020-03-08.
- yearfirst:表示传入数据的前两位数为年份。如‘030820’——>2003-08-20.
- format:自定义输出格式,如“%Y-%m-%d”.
- unit:可以为[‘D’, ‘h’ ,‘m’, ‘ms’ ,‘s’, ‘ns’]
- s 精确到秒
- ns 精确到纳秒
- infer_datetime_format:加速计算
- origin:自定义开始时间,默认为1990-01-01
DataFrame.groupby(key, as_index=False)
3.4 朴素贝叶斯算法
- 朴素:假设特征与特征之间是相互独立。
- 贝叶斯:贝叶斯公式。
- 注意:当我们的样本量不够导致计算某一些概率的时候出现了0的情况,我们怎么去解决?我们引入了 拉普拉斯平滑系数 ,这样就解决了。
3.4.1 什么是朴素贝叶斯分类方法
3.4.2 概率基础
概率(Probability)定义
- 概率定义为一件事情发生的可能性
- 扔出一个硬币,结果头像朝上
- 某天是晴天
- P(X) : 取值在[0, 1]
- 取值为0就是不可能事件
- 取值为1就是必然事件
女神是否喜欢计算案例
在讲这两个概率之前我们通过一个例子,来计算一些结果:
训练集:
| 样本数 | 职业 | 体型 | 女神是否喜欢 |
|---|---|---|---|
| 1 | 程序员 | 超重 | 不喜欢 |
| 2 | 产品 | 匀称 | 喜欢 |
| 3 | 程序员 | 匀称 | 喜欢 |
| 4 | 程序员 | 超重 | 喜欢 |
| 5 | 美工 | 匀称 | 不喜欢 |
| 6 | 美工 | 超重 | 不喜欢 |
| 7 | 产品 | 匀称 | 喜欢 |
测试集: 小明 产品 超重 ?
已知小明是产品经理,体重超重, 是否会被女神喜欢 二分类问题
- 问题如下:
1、女神喜欢的概率? P(喜欢) = 4/7
2、职业是程序员并且体型匀称的概率? P(程序员,匀称) = 1/7 联合概率
3、在女神喜欢的条件下,职业是程序员的概率? P(程序员 | 喜欢) = 2/4 = 1/2 条件概率
4、在女神喜欢的条件下,职业是程序员,体重是超重的概率? P(程序员,超重 | 喜欢) = 1/4 既符合联合概率,又符合条件概率
思考题: 在小明是产品经理并且体重超重的情况下,如何计算小明被女神喜欢的概率?
即P(喜欢|产品,超重)= ?
条件概率与联合概率
- 联合概率:包含多个条件,且所有条件同时成立的概率
- 记作:P(A,B)
- 例如: P(程序员,匀称) 、P(程序员,超重 | 喜欢)
- 特性:P(A, B) = P(A)P(B)
- 条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率
- 记作:P(A|B)
- 例如: P(程序员 | 喜欢) 、P(程序员,超重 | 喜欢)
- 特性:P(A1,A2|B) = P(A1|B)P(A2|B)
- 相互独立:如果P(A, B) = P(A)P(B),则称事件A与事件B相互独立。(充要条件)
3.4.3 贝叶斯公式
公式
计算案例
那么思考题就可以套用贝叶斯公式这样来解决
P(喜欢|产品,超重)= P(产品,超重|喜欢)P(喜欢)/P(产品,超重)
显然分母不能等于0。
上式中,P(产品,超重|喜欢)和P(产品, 超重)的结果均为0,导致无法计算结果。这是因为我们的样本量太少了,不具有代表性,本来现实生活中,肯定是存在职业是产品经理并且体重超重的人的,P(产品, 超重)不可能为0; 而且事件“职业是产品经理”和事件“体重超重”通常被认为是相互独立的事件,但是,根据我们有限的7个样本计算"P(产品, 超重)=P(产品)P(超重)"不成立。
而朴素贝叶斯可以帮助我们解决这个问题。
朴素贝叶斯,简单理解,就是假定了特征与特征之间相互独立的贝叶斯公式。
也就是说,朴素贝叶斯,之所以朴素,就在于假定了特征与特征相互独立。
朴素:
假设: 特征与特征之间是相互独立。
所以,思考题如果按照朴素贝叶斯的思路来解决,就可以是
p(产品, 超重) = P(产品)P(超重) =2/7 * (3/7) = 6/49
P(产品, 超重|喜欢) = P(产品|喜欢)P(超重|喜欢)=1/2 * 1/4 = 1/8
P(喜欢|产品, 超重) = P(产品, 超重|喜欢)P(喜欢)/P(产品, 超重)= 1/8 * 4/7 / 6/49 = 7/12
7/12这个结果显然也是不符合实际的,为什么会出现这么大的结果?
1. 样本量太少;
2. 是因为有这样一个假设(特征与特征之间是相互独立),产品经理和超重 根据我们的数据这两个之间也不是相互独立的,但是我们又假定了他们特征和特征之间是相互独立的,所以这个结果不是特别的准。
我们实际在用朴素贝叶斯算法的时候,我们接触的数据量是比较大的,所以那样就会稍微准一点。
朴素贝叶斯算法: 朴素 + 贝叶斯
朴素: 假设 特征与特征之间是相互独立。
贝叶斯 :贝叶斯公式
应用场景: 文本分类
为什么文本分类当中会比较常用?因为文章给它转换成能够被机器学习算法处理的数据,我们以单词作为特征,一般我们把一些词作为特征,有一个假设 就是词与词之间 相互独立的,所以我们也会经常把文本分类 用 朴素贝叶斯 去做。
那么这个公式如果应用在文章分类的场景当中,我们可以这样看:
公式分为三个部分:
- P( C ):每个文档类别的概率(某文档类别数/总文档数量)
- P(W│C):给定类别下特征(被预测文档中出现的词)的概率
- 计算方法:P(F1│C)=Ni/N (训练文档中去计算)
- Ni为该F1词在C类别所有文档中出现的次数
- N为所属类别C下的文档所有词出现的次数和
- 计算方法:P(F1│C)=Ni/N (训练文档中去计算)
- P(F1,F2,…) 预测文档中每个词的概率
我们知道了这些知识之后,继续回到我们的主题中。朴素贝叶斯如何分类,这个算法经常会用在文本分类,那就来看文章分类是一个什么样的问题?
P(科技|文章1)
P(娱乐|文章1)
这个了类似一个条件概率,那么仔细一想,给定文章其实相当于给定什么?结合前面我们将文本特征抽取的时候讲的?所以我们可以理解为
P(科技|文章1)=P(科技|词1, 词2,词3,词4.....)
P(娱乐|文章1)=P(娱乐|词1, 词2,词3,词4.....)
但是这个公式怎么求?前面并没有参考例子,其实是相似的,我们可以使用贝叶斯公式去计算
如果计算两个类别概率比较:
所以我们只要比较前面的大小就可以,得出谁的概率大
文章分类计算
| 文档ID | 文档中的词 | 属于c=China类 | |
|---|---|---|---|
| 训练集 | 1 | Chinese Beijing Chinese | Yes |
| 2 | Chinese Chinese Shanghai | Yes | |
| 3 | Chinese Macao | Yes | |
| 4 | Tokyo Japan Chinese | No | |
| 测试集 | 5 | Chinese Chinese Chinese Tokyo Japan | ? |
计算结果
P(C | Chinese,Chinese,Chinese,Tokyo,Japan) = P(Chinese,Chinese, Chinese,Tokyo,Japan | C) * P( C ) / P( Chinese,Chinese,Chinese,Tokyo,Japan)
P( 非C | Chinese,Chinese,Chinese,Tokyo,Japan) = P(Chinese,Chinese, Chinese,Tokyo,Japan | 非C) * P( 非C ) / P( Chinese,Chinese,Chinese,Tokyo,Japan)
P( C ) = 3/4
这时候我们前提已经是用的朴素贝叶斯算法了,那么这些特征与特征之间我们已经假定是相互独立的。
P(Chinese,Chinese, Chinese,Tokyo,Japan | C) = P(Chinese | C)^3 * P(Tokyo | C) * P(Japan | C)
P(Chinese | C)=5/8
P(Tokyo | C)=0/8 =0
P(Japan | C)=0/8 =0
思考:我们计算出来某个概率为0,合适吗?
概率=0那么肯定就不行啦,代入进去P(C | Chinese,Chinese,Chinese,Tokyo,Japan) = 0 ,岂不是P( 非C | Chinese,Chinese,Chinese,Tokyo,Japan)=100% 。
只能说是 可能 P(C | Chinese,Chinese,Chinese,Tokyo,Japan) 最少也只是0,但是不可能,因为我们根据常识来判断,在这篇文档当中,有三个词都是Chinese,所以这篇文章属于China概率是不可能为0的。
所以当我们概率在算P(Tokyo l C)=0 是不符合实际的,会让我们结果不准,那怎么办呢?
我们之所以在计算的过程中出现0,根本原因是 样本量 太少了,没有出现这个词,就导致我们在计算概率的时候使它为0了。那么怎么避免这种情况出现呢?
在这里我们需要引入一个叫做拉普拉斯平滑系数的东西。
拉普拉斯平滑系数
目的:防止计算出的分类概率为0
m=6
P(ChineselC) = (5+1) / (8+1*6) = 6/14 = 3/7
P(Tokyo|C) = (0+1) / (8+1*6) = 1/14
P(Japan|C) = (0+1) / (8+1*6) = 1/14
P(Chinese,Chinese, Chinese,Tokyo,Japan | C) = P(Chinese | C)^3 * P(Tokyo | C) * P(Japan | C) = (3/7)^3 * 1/14 * 1/14
API
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
3.4.4 案例:20类新闻分类
数据集可以用sklearn里自带的数据集,只不过是因为数据量比较大一点。用datasets.fetch_*()方法
分析
- 分割数据集
- tfidf进行的特征抽取
- 将文章字符串进行单词抽取
- 朴素贝叶斯预测
1)获取数据
因为我们是获取sklean里的数据,所以我们不用做数据处理
2)划分数据集
3)特征工程
文本特征抽取
4)朴素贝叶斯预估器流程
5)模型评估
代码
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def nb_news():
"""
用朴素贝叶斯算法对新闻进行分类
:return:
"""
# 1)获取数据
news = fetch_20newsgroups(subset="all") # subset= "train" 默认是获取训练集; "all"就是都要
# 2)划分数据集
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)
# 3)特征工程
# 文本特征抽取 -- tfidf
transfer = TfidfVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4)朴素贝叶斯预估器流程
estimator = MultinomialNB()
estimator.fit(x_train,y_train)
# 5)模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法二: 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
return None
if __name__ == "__main__":
nb_news()
运行结果
y_predict:
[ 0 3 7 ... 16 11 5]
直接比对真实值和预测值:
[ True False True ... True True True]
准确率为:
0.8391341256366723
报错:sklearn.datasets.fetch_20newsgroups下载报错问题urllib.error.HTTPError: HTTP Error 403: Forbidden
sklearn.datasets.fetch_20newsgroups离线下载导入
fetch_20newsgroups(20类新闻文本)数据集的安装
手动下载地址:https://people.csail.mit.edu/jrennie/20Newsgroups/20news-bydate.tar.gz
文件(20news-bydate.tar.gz、20news-bydate_py3.pkz )我放网盘里了 链接:https://pan.baidu.com/s/1XFWGZJopEeZGw3gIbGQeTg?pwd=1024
提取码:1024
下载之后得到一个文件,文件名是 20news-bydate.tar.gz
有文件了, Python 怎么读取?
fetch_20newsgroups函数将下载的文件放在C:\Users\你的用户名\scikit_learn_data\20news_home目录下
将你下载的文件放在这里 (没有的话创建一个)
Python下载的文件叫20news-bydate.tar.gz,你下载的名字是其他的,比如叫20newsbydate.tar.gz。改成它那样的就成(不过自己应该先看下, 你那个版本的Python下载的文件名字是啥)
复制你压缩包放的位置:C:\Users\eliauk\scikit_learn_data\20news_home\20news-bydate.tar.gz
进入Python安装文件夹中找到文件 _twenty_newsgroups.py
我的在C:\Users\eliauk\AppData\Local\Programs\Python\Python311\Lib\site-packages\sklearn\datasets
用任意文本编辑器打开它,找到 download_20newsgroups 函数
红色框是下载文件的部分, 绿色框是解压文件的部分
所以, 我们只需要将红色框注释掉, 并加入文件地址即可
然后, Ctrl + S 保存
"""
logger.info("Downloading dataset from %s (14 MB)", ARCHIVE.url)
archive_path = _fetch_remote(ARCHIVE, dirname=target_dir)
"""
archive_path = r'C:\Users\eliauk\scikit_learn_data\20news_home\20news-bydate.tar.gz'
有可能再报一个缩进的错: 看下哪行的4个空格变成一个Tab了, 改过来即可(我的是archive_path前面tab换成4个空格)
运行我们的代码
成功:
如果还是不行就卸载sklearn重装,再做一次上面修改_twenty_newsgroups.py文件这步,我就是这么解决的。
3.4.5 总结
-
优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快
-
缺点:
- 由于使用了样本属性独立性的假设,所以如果特征属性有关联时,其效果不好
- 我们在用朴素贝叶斯算法的时候,它是会计算一些概率值,如果本身样本给的就不是特别好的话,那么概率值算的也不是特别准,也会让最终的效果不是特别好。
-
应用场景:文本分类
3.5 决策树
找到最高效的决策顺序-比如说信息增益
1、认识决策树
决策树思想的来源非常朴素,程序设计中的条件分支结构就是if-then结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法
怎么理解这句话?通过一个对话例子
想一想这个女生为什么把年龄放在最上面判断!!!!!!!!!
决策树的思想:如何高效的进行决策
高效意味着,要决定一下特征的先后顺序。
那怎么才能知道哪个特征应该先看,哪个特征应该后看,而且这样比较高效呢?这就是我们决策树算法需要解决的问题。
2、决策树分类原理详解
为了更好理解决策树具体怎么分类的,我们通过一个问题例子?
已知 四个特征值 预测 是否贷款给某个人
类别指 是否贷款 给这个人。
问题:如何对这些客户进行分类预测?你是如何去划分?
有可能你的划分是这样的
那么我们怎么知道这些特征哪个更好放在最上面,那么决策树的真是划分是这样的
我们发现,凡是有房子的,最终都拿到贷款了。
如果新来的这个人,他是有房子的,那么我就能很快的做出决策,应该贷款给这个人。
如果这个人没有自己的房子,那应该采取怎样的措施呢?
就需要看训练集了,我们看到,没有自己房子的,就不一定给你贷款。
所以光看房子还不够,还得看你别的,比如是否有工作,如果有自己的工作,那么就应该贷款给这个人了。刚好这个人没有工作,就不贷款给这个人了。
1. 先看房子,再工作 -> 是否贷款 只看了两个特征
2. 年龄,信贷情况,工作 看了三个特征
很明显第二种方式就不高效,不如第一种高效
我们希望找到一种数学的方法,能够快速的自动的进行判断先看哪个特征 后看哪个特征,才能像第一种方式一样,很快速的知道结论 。
2.1 原理
- 信息熵、信息增益等
需要用到信息论的知识!!!问题:通过例子引入信息熵
- 1)信息
- 香农 定义的:消除随机不定性的东西 就是 信息
- 举个例子:有一个人她叫小依,小依她的年龄目前对我来说是未知的,现在我想知道小依今年多大了,我就问小依今年多少岁。
小依回答说:“我今年18岁” 。
如果说我一开始不知道小依的年龄 ,但是当小依告诉我 她今年18岁 ,这一瞬间,我就相当于 “我今年18岁”这句话就消除了我对于小依 年龄 的 不确定性。那么我们就认为这句话( “我今年18岁”)就是一个信息。 - 再举一个例子:现在我已经知道小依的年龄是18岁,那么当我和小依的这段对话进行完毕之后,小依的小微听到我们这段对话也抢着去说 ”小依明年19岁” ,这句话算信息吗?这句话不算信息。因为一开始,小依在说这句话(“我今年18岁”)之前,小依的年龄对于我来讲是不确定性的东西。当小依已经告诉我“我今年18岁” ,那么也就意味着这句话消除了我对于小依 年龄 的 不确定性,现在我已经知道小依的年龄是18岁,这时候小依的年龄对我来讲已经不是 不确定的东西了,所以小微说的这句话(”小依明年19岁”)他什么都没有消除,我已经知道她今年18岁了,我肯定也能推断出她明年是19岁,我还需要你告诉我吗?所以小微说的这句话基本上是废话(或者说是一个简单的推论),所以这句话(”小依明年19岁”)不是信息.
那么我们要如何去衡量我消除的这个不确定性的程度大小呢 ?
其实就是我们要去用量化,量化这个信息量,信息的大小其实就是我们 在消除不定性的 不确定性的程度大小是多少。
- 2)信息的衡量 - 信息量 - 信息熵
bit 比特
g(D,A) = H(D) - 条件熵H(D|A)
2.2 信息熵的定义
- H的专业术语称之为信息熵,单位为比特。
b随便你定,但是整个计算信息熵的过程当中,这个底数必须保持一致,一般在进行信息熵的计算,一般取2为底。
回到我们前面的贷款案例,去算一下信息熵
首先明确我们的任务:来了一个新的人,想要知道是否应该贷款给这个人,已知他的年龄、工作、房子、信贷情况,想要知道是否贷款给这个人。
现在其实我们转换成信息论里的语言的话,这个问题其实可以转换成 消除是否给这个人贷款的不确定性,现在我们在不知道这个人任何特征的情况下,应不应该贷款给这个人,是不是一个不确定性的东西呀?现在我就用信息熵来衡量这种不确定性的大小是有多少,就用到了信息熵的公式。
可以求总的信息熵 H(总) = -(6/15 * log 6/15 + 9/15*log9/15)=0.971 ,底数常用2。
现在我们知道他的总的不确定性是多少了,接下来我们怎么去确定我知道某一个特征之后,他这个不确定性减少的最多,是不是我们应该先看哪个特征?比如说我们一开始不知道这个人任何特征,有一个总不确定性是这么多0.971,当我们知道了其中一个年龄特征, 他是一个青年人,这种不确定性会减少。如果我们能够求出 知道某一个特征之后这个不确定性减少的程度,然后再比较哪一个 知道哪一个特征之后 这个不确定性减少的程度是最多的,我们是不是就可以先看它,这其实就是决策树来解决问题的一个思路。
接下来我们就需要求另一个不确定性,当知道某个特征之后,它的信息熵是多少,这样我们就引入了一个信息论里面另一个概念,叫做信息增益。
2.3 决策树的划分依据之一------信息增益
知道某一个特征之后这个不确定性减少的程度
定义与公式
特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差,即公式为:
信息增益 = 信息熵 - 条件熵
公式的详细解释:
注:信息增益表示得知特征X的信息而息的不确定性减少的程度使得类Y的信息熵减少的程度
贷款特征重要计算
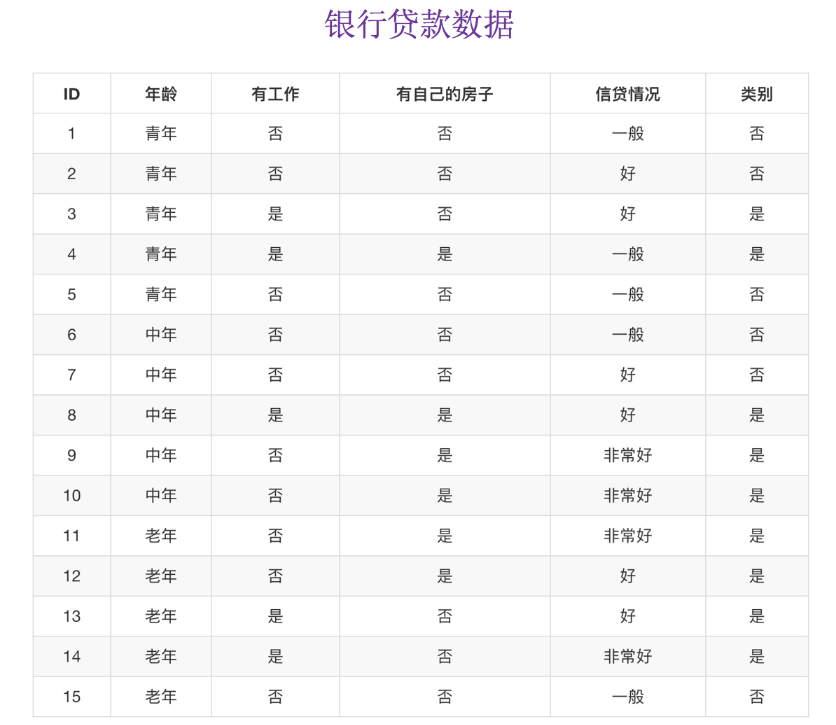
- 我们以年龄特征来计算:
1、g(D, 年龄) = H(D) -H(D|年龄) = 0.971-[5/15H(青年)+5/15H(中年)+5/15H(老年] 2、H(D) = -(6/15log(6/15)+9/15log(9/15))=0.971 3、H(青年) = -(3/5log(3/5) +2/5log(2/5)) 青年拿到贷款有2个 H(中年)=-(3/5log(3/5) +2/5log(2/5)) H(老年)=-(4/5og(4/5)+1/5log(1/5))
我们以A1、A2、A3、A4代表年龄、有工作、有自己的房子和贷款情况。最终计算的结果g(D, A1) = 0.313, g(D, A2) = 0.324, g(D, A3) = 0.420,g(D, A4) = 0.363。所以我们选择A3 作为划分的第一个特征。这样我们就可以一棵树慢慢建立。
2.4 决策树的三种算法实现
当然决策树的原理不止信息增益这一种,还有其他方法。但是原理都类似,我们就不去举例计算。
- ID3
- 信息增益 最大的准则
- C4.5
- 信息增益比 最大的准则
- CART
- 分类树: 基尼系数 最小的准则 在sklearn中可以选择划分的默认原则
- 优势:划分更加细致(从后面例子的树显示来理解)
3、 决策树API
- class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
- 决策树分类器
- criterion:默认是’gini’系数,也可以选择信息增益的熵’entropy’
- max_depth:树的深度大小
如果说我们不设定这个参数的话,那么这个决策树会尽可能的去拟合你所有的数据,使得决策树非常的大,但是它能够分的非常的细。如果你分的过细,你这个决策树模型能够拟合你所有的训练数据,很有可能它的泛化能力就比较差,就是说,它在这个训练集上可能表现的很好,但是在测试集上就表现不那么好,因为它过于拟合这个训练数据了,如果你设置一下这个树的深度大小,不让它过分的延展,是有可能能够提高它的准确率的。 - random_state:随机数种子
- 其中会有些超参数:max_depth:树的深度大小
- 其它超参数我们会结合随机森林讲解
4、决策树算法对鸢尾花分类
代码:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
def decision_iris():
"""
用决策树对鸢尾花进行分类
:return:
"""
# 1)获取数据集
iris = load_iris()
# 因为我们用的是鸢尾花数据集,直接就是sklean里的,里面分的挺好的,不用再做数据处理了
# 2)划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target,
random_state=22) # 我想要跟之前的KNN算法进行对比,所以我这个随机数种子设成一样的random_state=22
'''
由于我们并不是像KNN算法是需要计算距离的,我们这里是不用做特征工程(标准化)。
当然你也可以写特征工程做一些细节的,比如筛选一下特征,这个是看个人的,每个人做特征工程都是不一样的,
甚至我们说最后比赛你要跟不同的人进行比赛,如果你们用相同的算法,特征工程做的不一样,最后结果也是不一样的。
对数据的处理和特征工程是尽可能的使得我们这个算法能够得到更好的发挥,所以特征工程这个地方 你是可以有自己的想法 去创造的。
'''
# 3)使用决策树预估器
estimator = DecisionTreeClassifier(criterion='entropy') # max_depth参数就不写了,因为本身数据就不多,它不会做很深的延展,所以这个我们不设置也没关系
estimator.fit(x_train,y_train)
# 4)模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法二: 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
return None
if __name__ == '__main__':
decision_iris()
结果:
y_predict:
[0 2 1 2 1 1 1 1 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 1 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True False True True True True
True True True True True True False True True True True True
True True True True True False True True True True True True
True True]
准确率为:
0.9210526315789473
y_predict:
[0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True True True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True]
准确率为:
0.9736842105263158
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
我们发现同样划分数据集(随机数种子 random_state=22),我们之前用KNN算法准确率达到了0.97多,但是用决策树这个准确率只有0.92,准确率不是特别高。这个其实就体现了机器学习业界的一句著名的名言:“没有免费的午餐”。意思是机器学习业界总是有人想找到一个算法能够一劳永逸的解决任何一个问题,实际上 不同的算法(我是说在传统机器学习算法)它有不同的应用。
就比如说鸢尾花数据集,之所以在KNN上表现的更好,那是因为本身鸢尾花数据集本身就150个样本,我们之前分析KNN算法 它的缺点是什么?缺点就是它是一种懒惰算法,它的这个在预测的时候,它其实就是在疯狂的去计算在跟每个样本之间的距离,这时候内存消耗比较大,计算复杂度也比较高,它不但要计算距离 还要排序,找到最近的距离。由于我们数据量本身就不大,150个样本,即使做了这样的运算,它也能很快的出结果,最后结果还比较准确。
决策树的应用场景更适合用在数据量比较大的情况下,所以我们看到不同的算法,它是有不同的应用场景。在之后选择算法的时候,如果你一开始并不清楚这个场景应该用什么样的算法,那么你就可以多试几种不同的算法,看哪个效果好就用哪一个,这就是 对比 不同的算法处理同一个问题发现的情况。
保存树的结构到dot文件
决策树可视化
我们也说决策树它是可以进行可视化的,我们就很好奇我们刚刚在对鸢尾花进行分类的工程当中,这个树到底是怎么样的。
- sklearn.tree.export_graphviz() 该函数能够导出DOT格式
graph: 图
viz: Visualization 可视化- tree.export_graphviz(estimator,out_file='tree.dot’,feature_names=[‘’,’’])
export_graphviz(estimator,out_file="./tree.dot", feature_names=['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女性', '男性'])- estimator 预估器对象
- out_file 告诉你导出来的文件路径,名字tree、文件名后缀.dot文件
- feature_names 特征的名字,如果你不告诉它,也是可以导出来的,只不过会出现一些问题。
dot文件内容如下:
digraph Tree {
node [shape=box, fontname="helvetica"] ;
edge [fontname="helvetica"] ;
0 [label="x[2] <= 2.45\nentropy = 1.584\nsamples = 112\nvalue = [39, 37, 36]"] ;
1 [label="entropy = 0.0\nsamples = 39\nvalue = [39, 0, 0]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="x[3] <= 1.75\nentropy = 1.0\nsamples = 73\nvalue = [0, 37, 36]"] ;
0 -> 2 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
3 [label="x[2] <= 5.05\nentropy = 0.391\nsamples = 39\nvalue = [0, 36, 3]"] ;
2 -> 3 ;
4 [label="x[3] <= 1.65\nentropy = 0.183\nsamples = 36\nvalue = [0, 35, 1]"] ;
3 -> 4 ;
5 [label="entropy = 0.0\nsamples = 34\nvalue = [0, 34, 0]"] ;
4 -> 5 ;
6 [label="x[2] <= 4.75\nentropy = 1.0\nsamples = 2\nvalue = [0, 1, 1]"] ;
4 -> 6 ;
7 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 0, 1]"] ;
6 -> 7 ;
8 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1, 0]"] ;
6 -> 8 ;
9 [label="x[3] <= 1.55\nentropy = 0.918\nsamples = 3\nvalue = [0, 1, 2]"] ;
3 -> 9 ;
10 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 0, 2]"] ;
9 -> 10 ;
11 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1, 0]"] ;
9 -> 11 ;
12 [label="x[2] <= 4.85\nentropy = 0.191\nsamples = 34\nvalue = [0, 1, 33]"] ;
2 -> 12 ;
13 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1, 0]"] ;
12 -> 13 ;
14 [label="entropy = 0.0\nsamples = 33\nvalue = [0, 0, 33]"] ;
12 -> 14 ;
}
导出来之后我们可以查看一下,它其实是一个文本文件,我们是可以看到的。但是光看到这个文本文件,我们并没有看到树,要想看到树怎么办呢?我们需要借助一些工具把这个树显示出来。
-
网站显示结构
http://webgraphviz.com/
在网站当中点开,把文本文件拷到这,点击Generate Graph!,就可以看到我们生成的样子,这个树就出来啦!
树出来之后我们还是看不太懂,我们看不明白x[3]是什么还有x[2]这些又是什么东西呢?这其实就是因为我们刚刚在生成树结构的时候 没有去传特征的名字,那么我们就需要把特征的名字传进来,那我们就能看懂了。export_graphviz(estimator, out_file="./tree.dot", feature_names=iris.feature_names)
entropy计算信息增益
samples样本
- 工具: (能够将dot文件转换为pdf、png)
-
安装Graphviz
-
ubuntu:sudo apt-get install graphviz
-
Mac:brew install graphviz
-
windows版本:选择需要的版本就行了。
安装时勾选下面方框中的选项,将路径添加到系统路径中。(这一步不选的话就需要人为添加路径)
配置环境变量
如果上一步勾选了,这一步就不必要了。否则需要添加环境变量。将graphviz安装目录下的bin文件夹添加到Path环境变量中。我的安装目录如下,各自不同。D:\ProgramFiles\Graphviz\bin -
安装测试
进入命令行界面,输入dot -version,然后按回车,如果显示graphviz的相关版本信息,则安装配置成功。 -
运行命令
- 然后我们运行这个命令
dot -Tpng tree.dot -o tree.png
-
5、案例:泰坦尼克号乘客生存预测
文件(gender_submission )我放网盘里了 链接:https://pan.baidu.com/s/1XFWGZJopEeZGw3gIbGQeTg?pwd=1024
提取码:1024
https://www.kaggle.com/competitions/titanic/data
-
泰坦尼克号数据
训练数据集的基本情况:有11列属性,分别是乘客的ID、获救情况,乘客等级、姓名、性别、年龄、堂兄弟妹个数、父母与小孩的个数、船票信息、票价、船舱、登船的港口;从其中我们获取到几点认知:- PassengerId(乘客ID),Name(姓名),Ticket(船票信息)存在唯一性,三类意义不大,可以考虑不加入后续的分析;
- Survived(获救情况)变量为因变量,其值只有两类1或0,代表着获救或未获救;
- Pclass(乘客等级1,2,3,是社会经济阶层的代表。),Sex(性别),Embarked(登船港口)是明显的类别型数据,而Age(年龄),SibSp(堂兄弟妹个数),Parch(父母与小孩的个数)则是隐性的类别型数据;Fare(票价)是数值型数据;Cabin(船舱)则为文本型数据;
Age(年龄),Cabin(船舱)信息存在缺失数据。
流程分析:
特征值 目标值
1)获取数据
2)数据处理
缺失值处理age
特征值 -> 字典类型
pclass、age、sex这些都是类别,前面讲特征工程的时候,我们说当我们特征当中有很多类别的话,在sklean怎么处理会比较方便?我们特征当中如果有类别的话,要转换成one-hot编码,但是如果我们一个个转的话,pclass转一下age转一下再把sex转一下,就比较麻烦,如果有多个特征都是类别的话,我们先给它转换成字典,再用字典做特征抽取是不是就比较快呀?所以我们在这里要把特征值都转换成字典类型的,这样就比较方便。
3)准备好特征值 目标值
4)划分数据集
5)特征工程:字典特征抽取
决策树不需要做标准化
6)决策树预估器流程
7)模型评估
代码
为了数据展示方便,我们用jupyter notebook来做。
import pandas as pd
# 1.获取数据
titanic_train = pd.read_csv("./gender_submission/train.csv")
titanic_test = pd.read_csv("./gender_submission/test.csv")
titanic_train
titanic_test
# 筛选特征值和目标值
x = titanic_train[['Pclass', 'Age', 'Sex']]# 特征值
y = titanic_train["Survived"]# 目标值
x
y
# 2.数据处理
# (1)缺失值处理
x["Age"].fillna(x["Age"].mean(), inplace=True)
# x["age"].mean() 平均值
# inplace=True 改变原数据
x
# (2)转换成字典
x = x.to_dict(orient="records")# [{'Pclass': 3, 'Age': 22.0, 'Sex': 'male'},...,{}]
x
from sklearn.model_selection import train_test_split
# 3.数据集划分
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=22)
x_train
x_test
# 4. 字典特征抽取
from sklearn.feature_extraction import DictVectorizer
transfer = DictVectorizer()
type(transfer)
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
transfer.get_feature_names_out()# 返回类别名称
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
# 3)使用决策树预估器
estimator = DecisionTreeClassifier(criterion='entropy')
estimator.fit(x_train, y_train)
# 4)模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法二: 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
# 可视化决策树
export_graphviz(estimator, out_file="./titanic_tree.dot", feature_names=transfer.get_feature_names_out())
# 注意:feature_names不能直接传特征,当我们把Pclass、Age、Sex给他进行字典特征抽取之后,我们特征的名字是不是有变化呀?
# 本身 Pclass有三种,Sex有两种情况,转换成one-hot编码之后, 3*2个特征,所以我们怎么去写这个特征呀
# 用transfer.get_feature_names_out()
运行结果
准确率78%
如果我们想看生成的树的话,可以使用 命令dot -Tpng ./titanic_tree.dot -o titanic_tree.png 或者 在线网站 http://webgraphviz.com/看。
可以看到我们没有设置max_depth最大深度,这棵树就非常的大,这样就容易让我们结果不太准确,所以我们可以设置最大深度。
这个最大深度其实是可以调的,可以用网格搜索(Grid Search)去调的,比如我们可以先随便设置一个,它可能结果也不一定准确,感兴趣可以自己去调一调。
estimator = DecisionTreeClassifier(criterion='entropy',max_depth=6)
DataFrame.to_dict() 函数基本语法
- DataFrame.to_dict (self, orient='dict’, into=)
函数种只需要填写一个参数:orient 即可 ,但对于写入orient的不同,字典的构造方式也不同,官网一共给出了6种,并且其中一种是列表类型:- orient =‘dict’,是函数默认的,转化后的字典形式:{column(列名) : {index(行名) : value(值) )}};
- orient =‘list’ ,转化后的字典形式:{column(列名) :{[ values ](值)}};
- orient =‘series’ ,转化后的字典形式:{column(列名) : Series (values) (值)};
- orient =‘split’ ,转化后的字典形式:{‘index’ : [index],‘columns’ :[columns],’data‘ : [values]};
- orient =‘
records’ ,转化后是 list形式:[{column(列名) : value(值)}…{column:value}]; - orient =‘index’ ,转化后的字典形式:{index(值) : {column(列名) : value(值)}};
6、决策树总结
- 优点:
- 简单的理解和解释,树木可视化。
- 可视化 - 可解释能力强
- 缺点:
- 决策树学习者可以创建不能很好地推广数据的过于复杂的树,这被称为过拟合。
- 容易产生过拟合
- 改进:
- 减枝cart算法(决策树API当中已经实现,随机森林参数调优有相关介绍)
- 随机森林
注:企业重要决策,由于决策树很好的分析能力,在决策过程应用较多, 可以选择特征
总结:
- 信息熵、信息增益的计算
- DecisionTreeClassifier进行决策树的划分
- export_graphviz导出到dot文件
3.6 集成学习方法之随机森林
- 随机森林
- 随机
- 训练集随机
- 特征随机
- 森林
- 多个决策树
- 随机
3.6.1 什么是集成学习方法
集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测。
集成学习方法:三个臭皮匠顶个诸葛亮,或者说众人拾柴火焰高,少数服从多数,可能效果就会更好一点。
3.6.2 什么是随机森林
在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终投票结果就是True(少数服从多数)
3.6.3 随机森林原理过程
训练集:
N个样本
特征值 目标值
不管是决策树还是随机森林,其实都是根据特征值和目标值去进行预测的。
我们如果用决策树也好,随机森林也好,我们面对的训练集是一致的。
我如何对同样的一组训练集去产生多棵树呢?我怎么去产生树能够让这些树取得的结果 它的众数 预测的类别 是比较准确的呢?
如果说我不去随机的生成多棵树,我还是用原来的特征和目标,那我多棵树的结果是会一样,为了能够生成不同的树,
使得我们最终的结果可能会准确一点,所以我们要做这样的随机,不然我们就相当于把一个人给他复制好多遍,
他们思想都是一样的,然后再进行预测,那这样的结果肯定还是跟决策树是一样的,所以我们要做随机。
怎么随机呢?我们不仅让训练集随机,也要让特征也是随机的,
这样可以保持树的独立性,每一棵树单独的进行预测,最终去求一个众数,它可能结果就更准确一点。
M个特征
随机
两个随机
训练集随机 - N个样本中随机有放回的抽样N个
bootstrap 随机有放回抽样
举个例子,比如说我训练集总共有五个样本 [1, 2, 3, 4, 5]
新的树的训练集(也要保证它也是五个,从原始的数据当中抽一个,然后放回去,再抽一个,然后放回去,以此类推)
[2, 2, 3, 1, 5]
特征随机 - 从M个特征中随机抽取m个特征
M >> m 远远大于
起到 降维 的效果,也就降低了模型复杂度
由于每棵树的特征比较少,这样的话运算的速度会快一点。为什么我们不把所有的特征都用上呢?
如果说我们把这些特征,就是指每一棵树只取少量的一些特征,会不会影响结果呢?
其实经过时间检验,这样也是效果会比较好,他的一个原理就是 虽然 我这个特征数量变少了,
但是我们每一棵树它的特征数都是从M特征 抽取 m特征,这样的话就会有很多很多不同的树,
那如果说 这里面有聪明的树、有笨的树,"真理是掌握在少数人手中",笨的树之间是会相互抵消的,
聪明的树就脱颖而出,这是我们做的这样一个操作,不但可以达到降维的效果,而且还能够使得正确的结果脱颖而出。
学习算法根据下列算法而建造每棵树:
- 用N来表示训练用例(样本)的个数,M表示特征数目。
- 1、一次随机选出一个样本,重复N次, (有可能出现重复的样本)
- 2、随机去选出m个特征, m <<M,建立决策树
- 采取bootstrap抽样
为什么采用BootStrap抽样
- 为什么要随机抽样训练集?
- 如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的
- 为什么要有放回地抽样?
- 如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是“有偏的”,都是绝对“片面的”(当然这样说可能不对),也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决。
API
- class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
- 随机森林分类器
- n_estimators:integer,optional(default = 10)森林里的树木数量120,200,300,500,800,1200
- criterion: string,可选(default =“gini”)分割特征的测量方法, 默认是’gini’系数,也可以选择信息增益的熵’entropy’
- max_depth:integer或None,可选(默认=无)树的最大深度 5,8,15,25,30
- max_features="auto”,每个决策树的最大特征数量
- If “auto”, then max_features=sqrt(n_features).
对M求平方根 - If “sqrt”, then max_features=sqrt(n_features) (same as “auto”).
跟"auto"是一样的 - If “log2”, then max_features=log2(n_features).
对M求一个以2为底的对数 - If None, then max_features=n_features
每一个决策树它的特征数量还保持原来的M,这样就达不到降维的效果,可能每棵树在训练的时候就耗时比较长,当然还是得看情况分析,如果你发现数据量适合用M的话也可以设置成None。
- If “auto”, then max_features=sqrt(n_features).
- bootstrap:boolean,optional(default = True)是否在构建树时使用放回抽样,True 对训练集进行随机有放回的抽样
- min_samples_split:节点划分最少样本数
- min_samples_leaf:叶子节点的最小样本数
- 超参数:n_estimator, max_depth, min_samples_split,min_samples_leaf
案例:泰坦尼克号乘客生存预测
拿之前决策树写的代码改,这是一个传送门:3.5.5 案例:泰坦尼克号乘客生存预测
代码:
import pandas as pd
# 1.获取数据
titanic_train = pd.read_csv("./gender_submission/train.csv")
titanic_test = pd.read_csv("./gender_submission/test.csv")
titanic_train
titanic_test
# 筛选特征值和目标值
x = titanic_train[['Pclass', 'Age', 'Sex']]# 特征值
y = titanic_train["Survived"]# 目标值
x
y
# 2.数据处理
# (1)缺失值处理
x["Age"].fillna(x["Age"].mean(), inplace=True)
# x["age"].mean() 平均值
# inplace=True 改变原数据
x
# (2)转换成字典
x = x.to_dict(orient="records")# [{'Pclass': 3, 'Age': 22.0, 'Sex': 'male'},...,{}]
x
from sklearn.model_selection import train_test_split
# 3.数据集划分
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=22)
x_train
x_test
# 4. 字典特征抽取
from sklearn.feature_extraction import DictVectorizer
transfer = DictVectorizer()
type(transfer)
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
transfer.get_feature_names_out()# 返回类别名称
使用GridSearchCV进行网格搜索
### 随机森林对泰坦尼克号乘客的生存进行预测
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
estimator = RandomForestClassifier()
# 加入网格搜索和交叉验证
param_dict = { 'n_estimators': [120,200,300,500,800,1200], 'max_depth': [5,8,15,25,30] }
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
# 本身数据量有点大,而且是随机森林,每棵树都要折一折,所以我们少一点,3折交叉验证
estimator.fit(x_train, y_train) # 得到模型
# 5.模型评估
# 方法一: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 方法二: 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
print('最佳参数:\n', estimator.best_params_)
print('最佳结果:\n', estimator.best_score_)
print('最佳估计器:\n', estimator.best_estimator_)
print('交叉验证结果:\n', estimator.cv_results_)
注意
- 随机森林的建立过程
- 树的深度、树的个数等需要进行超参数调优
运行结果:
y_predict:
[1 0 0 1 1 0 1 0 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 0 0 1 1 1 0 0
0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 0 0 0
0 1 1 1 0 1 0 0 1 0 1 0 0 1 0 0 0 1 1 0 0 0 1 0 1 1 1 0 0 1 0 0 0 0 0 0 1
0 0 1 0 1 0 0 1 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 1 1 1 1 0 0 0 1 1 0 0
0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 1 0 0 0 1
1]
直接比对真实值和预测值:
816 False
789 True
869 False
235 False
473 True
...
174 True
723 True
350 True
399 True
194 True
Name: Survived, Length: 223, dtype: bool
准确率为:
0.7668161434977578
最佳参数:
{'max_depth': 5, 'n_estimators': 300}
最佳结果:
0.8159011028966185
最佳估计器:
RandomForestClassifier(max_depth=5, n_estimators=300)
交叉验证结果:
{'mean_fit_time': array([0.18271661, 0.29800733, 0.45868325, 0.74358773, 1.17621144,
1.73991203, 0.19956017, 0.36138312, 0.55342722, 0.90406013,
1.42640162, 2.21645776, 0.24630133, 0.39965733, 0.58607403,
1.00157801, 1.55887675, 2.33050219, 0.24627026, 0.39997888,
0.57047987, 0.96750299, 1.56504432, 2.33265138, 0.22518595,
0.39018949, 0.59265542, 0.96693651, 1.5720462 , 2.33341042]), 'std_fit_time': array([0.00992557, 0.00359695, 0.01208786, 0.02854672, 0.03827318,
0.05117431, 0.0122659 , 0.0211501 , 0.02416314, 0.01187686,
0.01632039, 0.04345188, 0.00093739, 0.00303068, 0.0091695 ,
0.03364935, 0.05145911, 0.0373619 , 0.02083582, 0.004264 ,
0.00928084, 0.04183131, 0.04362657, 0.04991704, 0.00529263,
0.01147206, 0.00657119, 0.04032525, 0.04885734, 0.07140804]), 'mean_score_time': array([0.00916219, 0.01524091, 0.02147659, 0.03420035, 0.05677454,
0.07874703, 0.00986155, 0.01568826, 0.02501766, 0.03750157,
0.06251574, 0.09623178, 0.01065318, 0.0166707 , 0.02367306,
0.03961563, 0.06486177, 0.09048827, 0.01066756, 0.01632142,
0.02335453, 0.04087973, 0.06262986, 0.09360846, 0.00966954,
0.01566768, 0.02401749, 0.03868651, 0.06235623, 0.09951369]), 'std_score_time': array([0.00045744, 0.00138772, 0.0026922 , 0.00120296, 0.00208017,
0.00123626, 0.00120822, 0.00043015, 0.00498382, 0.00388653,
0.00551026, 0.00448954, 0.00024675, 0.00093687, 0.00093845,
0.0002958 , 0.00119091, 0.00132241, 0.001247 , 0.00045856,
0.00048777, 0.00372039, 0.00098573, 0.00292948, 0.00047272,
0.00094274, 0.00123747, 0.00048561, 0.00086142, 0.00850526]), 'param_max_depth': masked_array(data=[5, 5, 5, 5, 5, 5, 8, 8, 8, 8, 8, 8, 15, 15, 15, 15, 15,
15, 25, 25, 25, 25, 25, 25, 30, 30, 30, 30, 30, 30],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object), 'param_n_estimators': masked_array(data=[120, 200, 300, 500, 800, 1200, 120, 200, 300, 500, 800,
1200, 120, 200, 300, 500, 800, 1200, 120, 200, 300,
500, 800, 1200, 120, 200, 300, 500, 800, 1200],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object), 'params': [{'max_depth': 5, 'n_estimators': 120}, {'max_depth': 5, 'n_estimators': 200}, {'max_depth': 5, 'n_estimators': 300}, {'max_depth': 5, 'n_estimators': 500}, {'max_depth': 5, 'n_estimators': 800}, {'max_depth': 5, 'n_estimators': 1200}, {'max_depth': 8, 'n_estimators': 120}, {'max_depth': 8, 'n_estimators': 200}, {'max_depth': 8, 'n_estimators': 300}, {'max_depth': 8, 'n_estimators': 500}, {'max_depth': 8, 'n_estimators': 800}, {'max_depth': 8, 'n_estimators': 1200}, {'max_depth': 15, 'n_estimators': 120}, {'max_depth': 15, 'n_estimators': 200}, {'max_depth': 15, 'n_estimators': 300}, {'max_depth': 15, 'n_estimators': 500}, {'max_depth': 15, 'n_estimators': 800}, {'max_depth': 15, 'n_estimators': 1200}, {'max_depth': 25, 'n_estimators': 120}, {'max_depth': 25, 'n_estimators': 200}, {'max_depth': 25, 'n_estimators': 300}, {'max_depth': 25, 'n_estimators': 500}, {'max_depth': 25, 'n_estimators': 800}, {'max_depth': 25, 'n_estimators': 1200}, {'max_depth': 30, 'n_estimators': 120}, {'max_depth': 30, 'n_estimators': 200}, {'max_depth': 30, 'n_estimators': 300}, {'max_depth': 30, 'n_estimators': 500}, {'max_depth': 30, 'n_estimators': 800}, {'max_depth': 30, 'n_estimators': 1200}], 'split0_test_score': array([0.79820628, 0.78475336, 0.79820628, 0.79820628, 0.79820628,
0.79820628, 0.78475336, 0.77578475, 0.77578475, 0.75784753,
0.75784753, 0.76233184, 0.78475336, 0.78026906, 0.78026906,
0.78475336, 0.78475336, 0.78026906, 0.78475336, 0.78026906,
0.78475336, 0.78026906, 0.78026906, 0.78026906, 0.78026906,
0.78475336, 0.78475336, 0.78026906, 0.78026906, 0.78475336]), 'split1_test_score': array([0.8161435 , 0.81165919, 0.81165919, 0.81165919, 0.81165919,
0.81165919, 0.81165919, 0.80717489, 0.79820628, 0.80269058,
0.79372197, 0.79372197, 0.78475336, 0.78026906, 0.78475336,
0.78475336, 0.78026906, 0.78475336, 0.78026906, 0.78026906,
0.78026906, 0.78026906, 0.78026906, 0.78026906, 0.78475336,
0.78026906, 0.78475336, 0.78026906, 0.78475336, 0.78026906]), 'split2_test_score': array([0.81531532, 0.83783784, 0.83783784, 0.83783784, 0.83783784,
0.83783784, 0.84684685, 0.84234234, 0.83783784, 0.84684685,
0.83333333, 0.84684685, 0.84234234, 0.81081081, 0.81081081,
0.82432432, 0.84234234, 0.82432432, 0.84684685, 0.82882883,
0.84234234, 0.82882883, 0.83333333, 0.84234234, 0.82882883,
0.82882883, 0.83333333, 0.84684685, 0.84684685, 0.84234234]), 'mean_test_score': array([0.80988836, 0.8114168 , 0.8159011 , 0.8159011 , 0.8159011 ,
0.8159011 , 0.8144198 , 0.80843399, 0.80394296, 0.80246165,
0.79496761, 0.80096689, 0.80394969, 0.79044964, 0.79194441,
0.79794368, 0.80245492, 0.79644892, 0.80395642, 0.79645565,
0.80245492, 0.79645565, 0.79795715, 0.80096015, 0.79795042,
0.79795042, 0.80094669, 0.80246165, 0.80395642, 0.80245492]), 'std_test_score': array([0.0082674 , 0.02167232, 0.0164552 , 0.0164552 , 0.0164552 ,
0.0164552 , 0.02542461, 0.0271866 , 0.02565578, 0.03633418,
0.03082953, 0.03488135, 0.02714771, 0.01439752, 0.01346559,
0.01865393, 0.02826402, 0.01979572, 0.03038331, 0.0228913 ,
0.02826402, 0.0228913 , 0.02501474, 0.02926163, 0.02191095,
0.02191095, 0.02290082, 0.03138507, 0.03038331, 0.02826402]), 'rank_test_score': array([ 7, 6, 1, 1, 1, 1, 5, 8, 12, 13, 28, 18, 11, 30, 29, 24, 15,
27, 9, 25, 15, 25, 21, 19, 22, 22, 20, 13, 9, 15])}
3.6.4 总结
- 在当前所有算法中,具有极好的准确率
- 能够有效地运行在大数据集上,处理具有高维特征的输入样本,而且不需要降维
- 能够评估各个特征在分类问题上的重要性
- 应用场景:高纬度特征,大数据场景 可以用到。
回归与聚类算法
4.1 线性回归
回忆一下回归问题的判定是什么?
回归问题: 目标值 - 连续型的数据
4.1.1 线性回归的原理
线性回归应用场景
- 房价预测
- 销售额度预测
- 金融:贷款额度预测、利用线性回归以及系数分析因子
什么是线性回归
函数关系 特征值和目标值
定义与公式
线性回归(Linear regression)是利用回归方程(函数) 对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
机器学习是来自于统计的,搞统计的这些人想到的去实现人工智能的一种途径,自变量和因变量是统计学当中的说法了,而在机器学习领域就喜欢叫特征值和目标值。
- 特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归
一个特征:y = kx + b 这也是属于线性模型
y = w1x1 + w2x2 + b
x 是特征值,h(w) 是目标值 以前用y表示,w是回归系数 或者叫权重值。b我们把它叫做偏置。
这其实是一个比较通用的线性回归的假定函数。
线性模型最通用的表示方法 y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
= wTx + b wT 表示w的转置
比较喜欢用矩阵来表示这种函数关系,这样我们就知道线性回归是怎么做的呢?首先假定了特征值和目标值 满足这样的一个函数关系,然后通过一些方法找到最合适的一组权重和偏置使得我们最终这个,这样的函数关系 能够正确的预测,而且预测的非常准,预测这个目标值,这就是我们 线性回归。在这里我们这个函数关系,我们给它取一个名字叫做线性模型。 它其实也是满足线性关系的。
回忆之前学数据挖掘基础的时候,有说表示学生的最终成绩,我们说他有平时成绩和期末成绩,我们是怎么去表示的呀?我们用的是矩阵乘法,
y = 0.7x1 + 0.3x2
期末成绩:0.7*考试成绩+0.3*平时成绩
[[90, 85],
[]]
[[0.3],
[0.7]]
[8, 2] * [2, 1] = [8, 1] 8行2列 * 2行1列 的一个矩阵,最后乘出来是8行1列的一个数。
那么怎么理解呢?我们来看几个例子
- 期末成绩:0.7×考试成绩+0.3×平时成绩
- 房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
上面两个例子,我们看到特征值与目标值之间建立的一个关系,这个可以理解为线性模型。
线性回归的特征与目标的关系分析
线性回归当中线性模型有两种,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征举例子。
- 线性关系
如果我们特征只有一个,这里这张图相当于特征只有房屋面积,这样的话就是一个平面,在一个平面当中我们看到,可以找到一条直线去拟合他们之间的关系,这样的话,他们之间的关系我们先假定一个线性模型 应该是怎么样的一种形式?y = kx + b ,当然k写成w权重也是可以的 就是字母的表示不一样而已。
如果有两个特征的话,其实就是在一个立体的空间当中,如果想要拟合X1、X2跟Y之间的关系的话,我们用怎么样的线性模型呀?y = w1x1 + w2x2 + b
注释:如果在单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想,记住这种关系即可
- 非线性关系
我们看到,x和y就不再是能用一条直线去拟合了,它是有这样的一个弯曲。如果想要用xy这种线性模型去表示,那么我们在用之前的这种y = kx + b ,因为它是在平面里面,而且还只有一个特征,如果按老方法只能用一条直线去拟合,但是我们看到,很显然这不是一条直线,但是这种其实也是线性模型。
为什么可以是线性模型呢?
其实线性模型它的定义,它的定义虽然它叫线性模型,但它的定义是这么来的。当你的这个函数关系当中,符合两种情况中的任意一种都是可以叫线性模型的,一种叫自变量是一次的,一种叫参数是一次的。
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b 就叫做自变量一次,一直都是一次的,没有高次的,所以这种啊就是满足自变量是一次的,这种是属于线性模型的。
y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + … + b 这种也可以叫线性模型,因为满足参数一次也可以叫线性模型,我们看这里,不管你特征值(自变量)x1还是x2 它们其实都有高次的,按理说如果按第一个定义它们肯定就不满足了,但是它们的参数(系数)w1w2w3w4甚至偏置b,都是一次的,所以这种也叫线性模型。但他们都已经不是线性关系了, 线性关系必须自变量是一次的,而我们现在虽然说自变量不是一次的了,但是由于它的参数是一次的,所以也可以叫线性模型。
注释:为什么会这样的关系呢?原因是什么?我们后面 讲解过拟合欠拟合重点介绍
如果是非线性关系,那么回归方程可以理解为:w1x1+w2x2^2+w3x3^2
广义线性模型
非线性关系?
线性模型
自变量一次
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
参数一次
y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + …… + b
线性关系一定是线性模型
线性模型不一定是线性关系
4.1.2 线性回归的损失和优化原理(理解记忆)
目标:求模型参数(权重w和偏置b)
模型参数能够使得预测准确
假设刚才的房子例子,真实的数据之间存在这样的关系
真实关系:真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
那么现在呢,我们随意指定一个关系(猜测)
随机指定关系:预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
当我们将一组特征值给带到假定的关系当中,那么我们得出的预测房屋价格跟真实房屋价格之间是不是肯定有一个误差呀?如果我们能通过一种方法,将这个误差不断的减少,让它最终接近于0的话,是不是就意味着我们这个模型参数是比较准确的呀,我们会通过一种方法不断的迭代更新我们的权重和偏置,使得预测值和真实值能够不断的缩小,最后我们能够越接近于0的时候,这个模型参数所对应的值就是我们要求的模型参数,这就是我们的思路。
真实值和预测值的差距,我们如何去衡量呢?我们把衡量的指标(衡量的关系)叫做损失函数, 也叫 cost, 也叫 成本函数, 也叫 目标函数。
这是我们需要先确定的东西,这个东西如何去确定呢? 往下看
请问这样的话,会发生什么?真实结果与我们预测的结果之间是不是存在一定的误差呢?类似这样样子
那么存在这个误差,我们将这个误差给衡量出来
真实结果与预测结果之间是存在一定误差的,如果是一个特征和一个目标的话就表示在一张平面上。看这张图,假如说我是随意先给了一条直线去预测房屋价格,我们也有真实的数据,这时候我们如何去衡量真实值和预测值之间的差距(误差)呢?
最好想到的就是去看距离,我们的目标就是希望找到所有真实的样本距离到预测之间的距离之和,如果能够让这个距离比较小,那就最终可以求出这个比较合适的权重和偏置。
损失函数
总损失定义为:
- y_i为第i个训练样本的真实值
- h(x_i)为第i个训练样本特征值组合预测函数
h(x_i) 就是我们的预测值 - (h(x_i)-y1)^2 为什么要平方?
因为有可能预测的值大于真实的值,也可能小于真实值,不管大了还是小了,它都是误差,为了能够把误差表示出来,就每一个样本在计算损失的时候都来一个平方,这样就不会出现我只是单纯的如果计算差值的话 那么最终正的和负的抵消了 反而使得我们损失本来很大,但是实际上求出来很小,所以我们就都乘了一个平方。 - 又称 最小二乘法
如何去减少这个损失,使我们预测的更加准确些?既然存在了这个损失,我们一直说机器学习有自动学习的功能,在线性回归这里更是能够体现。这里可以通过一些优化方法去优化(其实是数学当中的求导功能)回归的总损失!!!
我们把缩小损失的过程叫做优化损失
优化算法
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归经常使用的两种优化算法
- 正规方程
理解:X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果
优化损失
优化方法?
正规方程
天才 - 直接求解W
为什么可以一下子准确的得到准确的结果呢?
拓展:
1)
y = ax^2 + bx + c
y' = 2ax + b = 0
x = - b / 2a
其实正规方程就是这个思路,只不过这里x就不止一个了,而是有多个特征多个自变量,那就是一个特征值矩阵了,
这时候如果想要求损失函数最小值的话,那么它就会涉及到矩阵求导,至于矩阵求导怎么求就不往下展开了,
这个是有一些规则在的,感兴趣自行百度,它有一个矩阵求导,最后也是令矩阵求导等于0,最后去推,经过一系列的运算,
得出w=(X^TX)^-1X^Ty 这样的一个矩阵运算 最后能直接求解到最小值。
好处:比较直接,不用不断的试错,能直接得到好的结果。
这样的一种方式有什么不好吗?
缺点:如果特征比较多,比较复杂的话,那么这个求解速度是比较慢的,特别是在这里面还有一个求-1次方,
求幂是时间复杂度非常高的,非常不好求。所以正规方程一个是不如梯度下降广,只能在线性回归当中使用,
还有一个就是求解速度比较慢,在小数据场景下会比较有优势,但是数据量比较多的话就不太好了。
2)矩阵求幂
a * b = 1
b = 1 / a = a ^ -1
A * B = E
矩阵的求逆也是从这推广来的,放到矩阵的语境下就是:
矩阵A 乘以 矩阵B = 单位矩阵E
单位矩阵就是这样的一个形式,比如说
矩阵A和B如果都是3X3的矩阵的话,那么单位矩阵E也是一个二维:
[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]
矩阵A 乘以 矩阵B 如果最终等于这样的一个单位矩阵E 的话,
那么我们就说,矩阵B是 A的逆
B = A ^ -1
我们想要去求矩阵的逆的话,是非常麻烦的,所以正规方程这种优化方法只适合数据量比较小的情况。
梯度下降
勤奋努力的普通人
试错、改进
- 梯度下降(Gradient Descent)
理解:α为学习速率(沿着坡度最陡的方向,每次下降的步长),需要手动指定(超参数),α旁边的整体表示方向
沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新W值
使用:面对训练数据规模十分庞大的任务 ,能够找到较好的结果
我们通过两个图更好理解梯度下降的过程
所以有了梯度下降这样一个优化算法,回归就有了"自动学习"的能力
优化动态图演示
4.1.3 线性回归API
- sklearn.linear_model.LinearRegression(fit_intercept=True)
Regression回归- 通过正规方程优化
- fit_intercept:是否计算偏置
- LinearRegression.coef_:回归系数
- LinearRegression.intercept_:偏置
- sklearn.linear_model.SGDRegressor(loss=“squared_loss”, - fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
Regressor回归- SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
- eta0 学习率步长
- max_iter 迭代次数
我们说梯度下降它是不断的进行迭代的,那么这个迭代次数我们也是可以设定的 - loss:损失类型, 损失函数
- loss=”squared_loss”: 普通最小二乘法
- fit_intercept:是否计算偏置
- learning_rate : string, optional 学习率的算法
- 学习率填充,步长
- ‘constant’: eta = eta0
常数的意思,这样学习率就会一直保持在一个水平,都是eta0 - ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
- ‘invscaling’: eta = eta0 / pow(t, power_t)
为了提高优化的这个效率,它就一开始让这个步长很长,越接近这个最低点它会让步长缩小,我们默认的效果eta就代表你最终的学习率,每一次运算的学习率等于最初你给一个学习率eta0 除以 一个数的power_t次方,这样的话就可以导致你一开始学习率很大,随着我们训练 它这个学习率会越来越小,默认是0.25次方。- power_t=0.25:存在父类当中
- 对于一个常数值的学习率来说,可以使用learning_rate=’constant’ ,并使用eta0来指定学习率。
- SGDRegressor.coef_:回归系数
- SGDRegressor.intercept_:偏置
sklearn提供给我们两种实现的API, 可以根据选择使用
4.1.4 案例:波士顿房价预测
- 数据介绍
给定的这些特征,是专家们得出的影响房价的结果属性。我们此阶段不需要自己去探究特征是否有用,只需要使用这些特征。到后面量化很多特征需要我们自己去寻找
分析
回归当中的数据大小不一致,是否会导致结果影响较大。所以需要做标准化处理。同时我们对目标值也需要做标准化处理。
- 数据分割与标准化处理
- 回归预测
- 线性回归的算法效果评估
流程:
1)获取数据集
2)划分数据集
3)特征工程:
线性回归,我们假定他们特征值目标值满足怎样的一种关系?
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
= wTx + b
x1x2x3就是这样的一些特征,最终如果我们算出来这样的一个模型参数的话,如果说某一个特征本身数值是比较大的,有些特征的数值比较小,
也有可能导致最终学习到的模型它会有一些特征没学到,这个跟之前KNN算法有点像,KNN算法要算距离。
我们需要对波士顿房价数据集做什么样的处理?
无量纲化 - 标准化
4)预估器流程
fit() --> 模型
coef_ intercept_
5)模型评估
回归性能评估 - 均方误差
均方误差(Mean Squared Error)MSE评价机制:
注:y^i为预测值,¯y为真实值
y^i 的i是下标
其实就是拿每一个样本它的预测值-真实值,然后再求一个平方和,再求一个平均,我看着是不是有点眼熟?之前的损失函数,其实是跟它是一样的,只不过损失函数没有求平均 ,其实是一样的,有的时候我们也可以把均方误差也作为损失函数,都可以,用哪个作为损失函数都行。我们性能评估的时候也经常使用 均方误差。
损失函数
- sklearn.metrics.mean_squared_error(y_true, y_pred)
- 均方误差回归损失
- y_true:真实目标值
- y_pred:预测值
- return:浮点数结果,均方误差结果
哪一个模型它的均方误差比较小,就说明哪一个模型效果更好一点。
代码
sklearn 1.2版本之后没有boston数据集了, tensorflow里有数据集
命令pip install tensorflow安装tensorflow
# from sklearn.datasets import load_boston 1.2版本之后没有boston数据集了
# from sklearn.model_selection import train_test_split
# boston=load_boston()
# x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
import tensorflow as tf
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error
def linear1():
"""
正规方程的优化方法对波士顿房价进行预测
:return:
1)获取数据集
2)划分数据集
3)特征工程:标准化
4)预估器
5)得出模型
6)模型评估
"""
# 1)获取数据集
boston_housing = tf.keras.datasets.boston_housing
# 2)划分数据集
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
# print("特征数量:\n",x_train.shape)# 13 特征有几个权重系数就有几个
# print(x_train)
# print(x_test)
# print(y_train)
# print(y_test)
# 3)特征工程:标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.fit_transform(x_test)
# 4)预估器
estimator = LinearRegression()
estimator.fit(x_train,y_train)
# 5)得出模型
print("正规方程-权重系数为:\n",estimator.coef_)
print("正规方程-得出偏置为:\n",estimator.intercept_)
# 6)模型评估
y_predict = estimator.predict(x_test)
print("正规方程-预测房价:\n", y_predict)
error = mean_squared_error(y_test,y_predict)
print("正规方程-均方误差为:",error)
return None
def linear2():
"""
梯度下降的优化方法对波士顿房价
:return:
1)获取数据集
2)划分数据集
3)特征工程:标准化
4)预估器
5)得出模型
6)模型评估
"""
# 1)获取数据集
boston_housing = tf.keras.datasets.boston_housing
# 2)划分数据集
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
# 3)特征工程:标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.fit_transform(x_test)
# 4)预估器
estimator = SGDRegressor()
estimator.fit(x_train,y_train)
# 5)得出模型
print("梯度下降-权重系数为:\n",estimator.coef_)
print("梯度下降-得出偏置为:\n",estimator.intercept_)
# 6)模型评估
y_predict = estimator.predict(x_test)
print("梯度下降-预测房价:\n", y_predict)
error = mean_squared_error(y_test,y_predict)
print("梯度下降-均方误差为:",error)
return None
if __name__ == "__main__":
# 代码1:正规方程的优化方法对波士顿房价进行预测
linear1()
# 代码2:梯度下降的优化方法对波士顿房价进行预测
linear2()
结果:
正规方程-权重系数为:
[-1.10749194 1.35308963 0.02710126 0.9943535 -2.40156557 2.3962877
0.2111952 -3.47121628 2.90814885 -1.95741889 -1.98298545 0.81955092
-4.02739073]
正规方程-得出偏置为:
22.39504950495051
正规方程-预测房价:
[ 5.55451294 20.00731644 20.55665365 32.82302446 25.64697477 19.45968834
29.28312483 25.38391555 18.77010357 21.69493081 18.90073817 17.19404589
14.76462193 35.36471844 16.94182469 20.19279347 24.81663854 21.40019897
18.73374643 21.50058781 9.01360171 14.22493901 21.76783427 13.19477724
22.92466903 22.95855583 32.30713014 26.99577554 10.29743999 21.23053674
22.74987751 16.53696011 35.95251346 23.61151789 16.90051536 1.47956779
11.91196969 21.84417768 14.98432038 28.78391568 23.44723764 28.43262246
15.54312803 34.89119042 30.93811614 24.03029827 30.94630116 17.31001806
21.29586521 23.85376225 32.55122546 18.85538009 7.39134469 12.50987673
35.31802235 27.58130985 15.22470224 40.22803819 37.31630734 24.68154074
24.58704989 18.47862137 17.33356639 20.33194398 24.51156031 25.44348413
15.17899598 27.98967896 1.61585283 7.79000193 21.99030399 25.19471673
22.64422388 6.58951295 29.16926758 21.24881594 20.91593148 24.45613791
34.58678744 3.31253496 24.01003208 36.60015237 16.62435866 15.77682186
19.8823582 18.7739659 20.10582024 24.41995009 22.4085753 28.25894098
17.1408851 17.99213613 27.42088419 29.91688329 35.52379739 18.55880041
35.9671986 37.01310323 25.17154407 40.6431914 33.44709717 24.26252215]
正规方程-均方误差为: 20.982945190702562
梯度下降-权重系数为:
[-1.05524559 1.2609661 -0.20072048 1.02818909 -2.3003646 2.4488571
0.13092105 -3.42745777 2.19277374 -1.2086418 -1.9462163 0.83041436
-3.99309211]
梯度下降-得出偏置为:
[22.39518279]
梯度下降-预测房价:
[ 5.49263091 20.32115164 20.38942754 32.86283015 25.62440723 19.80020477
29.5892854 25.3486887 17.93148204 21.46388075 19.16509493 17.27162955
15.02092722 35.31406691 16.69521034 20.19516665 24.91429584 22.20220653
18.5025951 21.50947091 8.80848359 14.01712816 21.70007989 13.10397158
23.13807298 22.7100683 32.22650531 26.42271933 10.13957734 21.53567571
23.12640367 16.32001279 35.87426678 23.70113486 16.75751647 1.45797363
12.11931741 21.81369136 16.18434815 28.70278838 23.45811533 28.67223111
15.41383133 34.89207465 30.67198267 23.8511228 30.47276617 17.33620525
21.15170471 23.7729434 32.19955158 18.62479109 7.21622954 12.5997249
35.67477121 27.60306876 15.13224214 40.1773403 37.20066946 24.63017909
24.43799682 18.33126719 17.15953474 20.61336027 24.49695742 25.62528794
15.04329371 27.72588788 2.77453499 7.80867668 21.99054945 25.32553587
22.30977383 7.74524636 29.07866073 21.17015955 21.19372512 24.41644189
34.27731485 3.16254386 23.78268966 36.48668717 16.48227274 15.69574541
19.8613809 18.69687412 19.93364321 24.13897556 22.56524034 28.02004832
16.97238849 18.59023294 27.31101544 30.1499067 35.19849782 18.75696188
35.80835034 37.11426542 25.50250887 40.78790203 33.33099427 24.20937904]
梯度下降-均方误差为: 20.78205610771906
我们梯度下降是可以传参数的:
estimator = SGDRegressor(eta0=0.001,max_iter=10000) # eta0学习率步长,max_iter迭代次数
结果:我们看到这个误差变小了
梯度下降-均方误差为: 20.255441228505354
还有其他参数,learning_rate 学习率的算法
estimator = SGDRegressor(learning_rate="constant",eta0=0.001,max_iter=10000) # eta0学习率步长,max_iter迭代次数
梯度下降-均方误差为: 20.665643424590826
我们也可以尝试去修改学习率,此时我们可以通过调参数,找到学习率效果更好的值。
规方程和梯度下降对比
- 文字对比
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
- 选择:
- 小规模数据:
- LinearRegression(不能解决拟合问题)
- 岭回归
- 大规模数据:SGDRegressor
- 小规模数据:
4.1.5 拓展-关于优化方法GD、SGD、SAG
GD
梯度下降(Gradient Descent),原始的梯度下降法需要计算所有样本的值才能够得出梯度,计算量大,效率低,所以后面才有会一系列的改进。
SGD
随机梯度下降(Stochastic gradient descent)是一个优化方法。它在一次迭代时只考虑一个训练样本。
- SGD的优点是:
- 高效
- 容易实现
- SGD的缺点是:
- SGD需要许多超参数:比如正则项参数、迭代数。
- SGD对于特征标准化是敏感的。
SAG
随机平均梯度法(Stochasitc Average Gradient),由于收敛的速度太慢,有人提出SAG等基于梯度下降的算法
Scikit-learn:SGDRegressor、岭回归、逻辑回归等当中都会有SAG优化
总结
- 线性回归的损失函数-均方误差
- 线性回归的优化方法
- 正规方程
- 梯度下降
- 线性回归的性能衡量方法-均方误差
- sklearn的SGDRegressor API 参数
4.2 欠拟合与过拟合
问题:训练数据训练的很好啊,误差也不大,为什么在测试集上面有问题呢?
当算法在某个数据集当中出现这种情况,可能就出现了过拟合现象。
什么是过拟合与欠拟合
- 欠拟合
学习到的特征太少了 - 过拟合
学习到的特征太多了 - 分析
- 第一种情况:因为机器学习到的天鹅特征太少了,导致区分标准太粗糙,不能准确识别出天鹅。
- 第二种情况:机器已经基本能区别天鹅和其他动物了。然后,很不巧已有的天鹅图片全是白天鹅的,于是机器经过学习后,会认为天鹅的羽毛都是白的,以后看到羽毛是黑的天鹅就会认为那不是天鹅。
定义
- 过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在测试数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
- 欠拟合:一个假设在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
有一个临界值,临界值大概在这个位置,根据这个临界点得出模型过拟合和欠拟合的区分
那么是什么原因导致模型复杂?线性回归进行训练学习的时候变成模型会变得复杂,这里就对应前面再说的线性回归的两种关系,非线性关系的数据,也就是存在很多无用的特征或者现实中的事物特征跟目标值的关系并不是简单的线性关系。
原因以及解决办法
- 欠拟合原因以及解决办法
- 原因:学习到数据的特征过少
- 解决办法:增加数据的特征数量
- 过拟合原因以及解决办法
- 原因:原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决办法:
- 正则化
在这里针对回归,我们选择了正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题,除了一些算法本身作用之外(决策树、神经网络),我们更多的也是去自己做特征选择,包括之前说的删除、合并一些特征
如何解决?
在学习的时候,数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多,所以算法在学习的时候尽量减少这个特征的影响(甚至删除某个特征的影响),这就是正则化
注:调整时候,算法并不知道某个特征影响,而是去调整参数得出优化的结果
正则化类别
-
L2正则化 更常用
- 作用:可以使得其中一些W(权重系数)的都很小,都接近于0,削弱某个特征的影响
- 优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象
- L2惩罚项(λ惩罚项 )还有一个名字叫 Ridge回归 - 岭回归
- 加入L2正则化后的损失函数:
损失函数 + λ惩罚项
注意:m为样本数,n为特征数
这个惩罚项有什么好处呢?这个惩罚项由每一个权重的 权重值平方 求和,惩罚项前面还有一个系数,它有怎样的效果?因为我们整个线性回归 它这个优化是怎么优化?是不是尽可能让损失函数变小呀,现在我们在损失函数本身后面加上一个惩罚项,也就意味着我们在优化损失的过程当中也会使得 权重系数变小,这样的话 如果你让最终的结果取得最小值 它的效果就是 不仅让你的损失变小了 还让你的权重系数尽可能的减小。所以这样就达到了理想的效果,不仅能够让我们的模型能够更加的准确,还消除了一些高次项的影响,如果让我们权重系数 它自己变小了 是不是这个特征就相当于对最终的模型影响 微乎其微了。这个就是我们正则化的原理,通过加上一个惩罚项使得w权重值能够自动的缩小,前面的系数λ可以理解为惩罚的步长,这个系数也可以是一个超参数 也是可以调的。
-
L1正则化
- 作用:可以使得其中一些W的值直接为0,删除这个特征的影响
- L1惩罚项(λ惩罚项 )还有一个名字叫 LASSO回归
- 损失函数 + λ惩罚项
也是相当于 损失函数 + λ惩罚项 , 只不过这个惩罚项就不在是w的平方,而是w的绝对值,L1正则化是w的绝对值加一起,L2正则化的是w的平方加一起,如果是w的绝对值加在一起,它的一个效果会使得线性模型中权重系数的值(w)直接为0,相当于删除了某列的特征,所以我们说用L2正则化会多一点,L2是比较缓和 削弱某些特征的影响,而L1是直接删除这个特征的影响。
拓展-原理(了解)
线性回归的损失函数用最小二乘法,等价于当预测值与真实值的误差满足正态分布时的极大似然估计;岭回归的损失函数,是最小二乘法+L2范数,等价于当预测值与真实值的误差满足正态分布,且权重值也满足正态分布(先验分布)时的最大后验估计;LASSO的损失函数,是最小二乘法+L1范数,等价于等价于当预测值与真实值的误差满足正态分布,且且权重值满足拉普拉斯分布(先验分布)时的最大后验估计
4.3 线性回归的改进-岭回归
带有L2正则化的线性回归-岭回归
岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上正则化的限制,从而达到解决过拟合的效果
API
- sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)
- 具有l2正则化的线性回归
- alpha:正则化力度(也叫 惩罚项系数),也叫 λ
- λ取值:0~1 1~10
- solver:会根据数据自动选择优化方法
- sag:如果数据集、特征都比较大,选择该随机梯度下降优化
- normalize:数据是否进行标准化
- normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
- normalize如果选择True的话,其实跟我们在特征工程当中先做一个StandardScaler然后再进行预估器效果流程是一样的,也就是说你要是把normalize设置成True我们就不用再做标准化。
- Ridge.coef_:回归权重
- Ridge.intercept_:回归偏置
All last four solvers support both dense and sparse data. However,
only ‘sag’ supports sparse input when `fit_intercept` is True.
Ridge方法相当于SGDRegressor(penalty='l2', loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习,推荐使用Ridge(实现了SAG)
- sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
- 具有l2正则化的线性回归,可以进行交叉验证
- coef_:回归系数
class _BaseRidgeCV(LinearModel):
def __init__(self, alphas=(0.1, 1.0, 10.0),
fit_intercept=True, normalize=False, scoring=None,
cv=None, gcv_mode=None,
store_cv_values=False):
观察正则化程度的变化,对结果的影响?
- 正则化力度(λ) 越大,权重系数会越小
- 正则化力度越小,权重系数会越大
案例:波士顿房价预测
拿之前的代码改,改预估器为Ridge就好啦
import tensorflow as tf
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
def linear3():
"""
岭回归对波士顿房价进行预测
:return:
"""
# 1)获取数据集
boston_housing = tf.keras.datasets.boston_housing
# 2)划分数据集
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
# 3)特征工程:标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4)预估器
estimator = Ridge() #
estimator.fit(x_train, y_train)
# 5)得出模型
print("岭回归-权重系数为:\n", estimator.coef_)
print("岭回归-得出偏置为:\n", estimator.intercept_)
# 6)模型评估
y_predict = estimator.predict(x_test)
print("岭回归-预测房价:\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("岭回归-均方误差为:", error)
return None
if __name__ == "__main__":
# 代码3 岭回归
linear3()
岭回归-权重系数为:
[-1.09617853e+00 1.33240158e+00 2.36163129e-03 9.96960412e-01
-2.36364456e+00 2.41020778e+00 2.00070026e-01 -3.43427327e+00
2.81042350e+00 -1.86812093e+00 -1.97196416e+00 8.20257578e-01
-4.00831026e+00]
岭回归-得出偏置为:
22.39504950495051
岭回归-预测房价:
[ 5.59719934 20.03120425 20.54494663 32.79149688 25.61772824 19.49769659
29.3083976 25.35790046 18.68088247 21.66007634 18.92431032 17.2203747
14.81668779 35.34173677 16.89901794 20.20973415 24.81922648 21.49646988
18.70775424 21.5231452 9.0000082 14.18971933 21.74340972 13.21240084
22.94391104 22.9096517 32.27480305 26.95382138 10.3103409 21.26089585
22.78102916 16.51789473 35.90449534 23.61319736 16.87780052 1.52008639
11.99397496 21.83020283 15.13664148 28.7643829 23.48908701 28.43155048
15.55308818 34.87281201 30.87073977 23.99268193 30.8486107 17.32528916
21.29455886 23.83459435 32.49808863 18.83940581 7.3922619 12.54854547
35.31401526 27.56816271 15.2364521 40.19991707 37.25080168 24.67369048
24.56682951 18.47497386 17.31788794 20.36156947 24.50565578 25.45491716
15.19147467 27.93454022 1.78585749 7.83591935 22.01434692 25.23671468
22.58227731 6.74885895 29.13005659 21.25382938 20.94410053 24.44442511
34.51987694 3.32599905 23.96377657 36.56720924 16.62212001 15.80077782
19.87966223 18.78987635 20.07777226 24.37834562 22.43414093 28.21123568
17.13976565 18.08895035 27.40271006 29.98608733 35.43887428 18.6291036
35.92420424 37.03853037 25.18980557 40.63696642 33.40452764 24.24148884]
岭回归-均方误差为: 20.899200400251683
我们还可以改一下参数
estimator = Ridge(alpha=0.5,max_iter=10000) # max_iter 迭代次数
这个就自己慢慢调了哈
岭回归-均方误差为: 20.94010694487814
SGDRegressor默认penalty=“l2” 也是带l2正则化,它其实也相当于是岭回归了
如果我把penalty设置成"l1",我们可以看一下,就是LASSO了。
estimator = SGDRegressor(learning_rate="constant", eta0=0.001, max_iter=10000, penalty="l1")
梯度下降-均方误差为: 20.860241268410334
4.4 分类算法-逻辑回归与二分类
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广泛。
逻辑回归是一种用于解决二分类问题的统计学方法。
它的输入是线性回归的结果,然后通过sigmoid函数将整体值映射到0和1之间,再设置一个阈值进行分类判断。sigmoid函数可以把任何连续的值映射到0和1之间,这样就可以把线性回归的结果解释为概率值。一般情况下,如果概率值大于0.5,就判断为正样本,如果概率值小于0.5,就判断为负样本。
4.4.1 逻辑回归的应用场景
- 广告点击率 - 是否会被点击
- 是否为垃圾邮件
- 是否患病
- 金融诈骗 - 是否为金融诈骗
- 虚假账号 - 是否为虚假账号
正例 / 反例
看到上面的例子,我们可以发现其中的特点,那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。
4.4.2 逻辑回归的原理
输入
看这个公式是不是可非常熟悉?线型回归的输出 就是 逻辑回归 的 输入
逻辑回归的输入就是一个线性回归的结果。
激活函数
-
sigmoid函数
1/(1 + e^(-x))
将h(w)代入到x这个部分就成了最终这个结果
θT写的就是另一种线性模型的表示方法,例如:还可以用矩阵的形式来表示wTx + b,所以就我们看到的这样的写成这种形式了。 -
分析
- 回归的结果输入到sigmoid函数当中
- 输出结果:[0, 1]区间中的一个概率值,默认为0.5为阈值
SIGMOD函数:将某个函数映射到 0 - 1 的区间之内
h(w)代入到x,代入到这里有什么好处呢?
1/(1 + e^(-x)) sigmoid函数图像就是它,1/(1 + e^(-x))它的值域就是在[0, 1]区间的一个值,所以当我们把任何一个线性回归的一个输出带入到sigmoid函数当中,它就会被映射到[0, 1]区间。
映射到[0, 1]区间,这样有什么效果呢?
我们可以把[0, 1]区间看成是概率值,既然是一个概率值,我们是不是可以看它属于这个类别的可能性是多少,如果我们在设定一个阈值,比如说我们一般设定0.5为阈值,那我们上一步输出的结果把它映射到sigmoid函数后出现的这个结果如果大于那么就认为属于这个类别;如果小于0.5,就认为不属于这个类别,那我们是不是就将一个回归给他转成成分类了,那么就可以完成一个分类任务了。这就是逻辑回归它之所以名叫回归却可以用来分类的原因所在。
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)。(方便损失计算)
现在还有一个问题,我们现在相当于已经有了一个假设函数,也就是说相当于有了一个模型(线性模型) ,这回也叫线性模型 只不过线性模型要经过一定的处理给它转换成概率值 ,这个模型比较完整的写法:
1/(1 + e^(-(w1x1 + w2x2 + w3x3 + …… + wnxn + b)) )
现在我们 如何得出 一组权重和偏置 使得 我们这个模型可以准确的进行分类预测呢? 这是我们接下来要解决的问题 ,那么如何解决呢?
既然它也是属于一种线性模型,那我们是不是可以用类似于 求线性回归的模型参数方法 来去构建一个损失函数,有了这个损失函数之后 我们也是用一种优化方法 将损失函数能够让它取得最小值,当损失函数取得最小值的时候,它所对应的权重值 就是我们想要求出来的模型参数,我们可以用这样的一个思路 优化损失。现在关键是这个损失函数如何去确定呢? 之前线性回归的损失函数是什么?最小二乘法或者均方误差 这些都可以衡量真实值和预测值之间的误差,我们用的是 (y_predict - y_true)平方和/总数 ,这个还算好构建,但我们逻辑回归真实值是什么?逻辑回归真实值是不是分类呀,是否属于某个类别,而我们这个线性回归的时候,它的真实值就是具体的一个数,我们根据这个模型得出了一个预测值 然后再减去这个真实值 求平方和 求平均,均方误差这个没有问题,但是我们这是逻辑回归,真实值是 是否属于某个类别,我们线性模型经过sigmoid映射之后到[0,1]区间,它是一个概率值,然后我们再跟阈值进行判断能够知道它是否属于这个类别,也就是说我们这个预测值 也是 是否属于这个类别,这样的话我们好像还是挺难去确定我们的损失函数的,之前是 具体的值(y_predict) 我们相减(- y_true)求一个差 没有问题,现在我们是真实值和预测值都是属于某个类别,我们如何去确定这个损失函数呢?我们肯定是已经没有办法再用之前的均方误差、最小二乘法 了,这时候我们需要引入另外一种损失函数的构建方法,叫做对数似然损失。
输出结果解释(重要):假设有两个类别A,B,并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.6,那么这个概率值超过0.5,意味着我们训练或者预测的结果就是A(1)类别。那么反之,如果得出结果为0.3那么,训练或者预测结果就为B(0)类别。
所以接下来我们回忆之前的线性回归预测结果我们用均方误差衡量,那如果对于逻辑回归,我们预测的结果不对该怎么去衡量这个损失呢?我们来看这样一张图
那么如何去衡量逻辑回归的预测结果与真实结果的差异呢?
损失以及优化
损失
逻辑回归的损失,称之为对数似然损失,公式如下:
- 分开类别:
分段函数
先是这样一个分段函数,如果y=1就是告诉我们真实值是属于这个情况,那么这个损失就是-log(hθ(x)); 如果这个真实值是0,也就是说不属于这个类别的话,那么损失是-log(1-hθ(x)) 。
怎么理解单个的式子呢?这个要根据log的函数图像来理解
线性回归的输出有一个值,把它映射到 sigmoid函数上,它就会在[0,1]区间有一个值,这个值如果越接近于1,是不是说明我们预测的越准确呀,那我们看相应的函数图像是不是意思告诉我们这个损失是接近于0的呀,也就是说当真实值为1我们这个损失函数也是接近于0,这是不是符合我们对损失函数的定义呀。如果说我经过映射之后是一个接近于0的这样的概率值的话,是不是就意味着我们预测的不准呀,也就意味着我们最终损失非常大呀,那我们看这个在这个函数图像上也可以看出 相应的 纵轴值 就是损失值 是趋向于无穷大,所以我们这个分段函数就是当真实值属于这个类别,就可以这么去理解。
同理,我们也可以画出当 y=0 时,函数 C(θ) 的图像:
- 综合完整损失函数
但是我们将这个损失定义为一个分段函数的话就很难去用什么 梯度下降 去优化了 对吧?所以我们一般写对数自然函数的时候会写成 这样一个完整的表达式。但是我们将这个损失定义为一个分段函数的话就很难去用什么 梯度下降 去优化了 对吧?所以我们一般写对数自然函数的时候会写成 这样一个完整的表达式。这个表达式我们看,是这样写的,我们需要对样本当中每一个样本都进行预测,去衡量它跟真实值之间的误差,最后求一个和,每一个样本做怎样的计算呢?那就是后面这个长长的一个式子
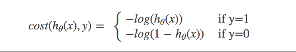
yi 是真实值
看到这个式子,其实跟我们讲的信息熵类似。
看到这个式子,其实跟我们讲的信息熵类似。
我们已经知道,-log(P), 例如 -log 2 x,P值越大,结果(
-log(P) )越小,所以我们可以对着这个损失的式子去分析
我们拿到这样一个损失函数,就可以去衡量逻辑回归当中预测值和真实值之间的误差了,所以我们看当我们给我们模型输入一组特征值,然后进行一个线性回归,也就是这块的内容w1x1 + w2x2 + w3x3 + …… + wnxn + b 拿到它之后我们就有了线性回归的输出,然后让这组输出统一的经过一个sigmoid映射,把它映射到一个[0,1]区间的值,这时候我们来一个阈值(阈值你可以自己定,我们一般默认是0.5),超过0.5就属于这个类别,不超过就是不属于这个类别,这样的话我们看0.4就是不属于 -> 预测为0;0.68就是属于 -> 预测为1 ……我们看到只有最后一个预测对了,这样的话我们可以根据上面这个 综合完整损失函数 公式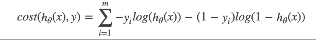
优化
同样使用梯度下降优化算法,去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率。
4.4.3 逻辑回归API
- sklearn.linear_model.LogisticRegression(solver=‘liblinear’, penalty=‘l2’, C = 1.0)
LogisticRegression逻辑回归- solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数),按默认的就可以了。
- sag:根据数据集自动选择,随机平均梯度下降
- penalty:正则化的种类
- C:正则化力度
- solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数),按默认的就可以了。
默认将类别数量少的当做正例
LogisticRegression方法相当于 SGDClassifier(loss=“log”, penalty=" "),SGDClassifier实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置average=True。而使用LogisticRegression(实现了SAG)
Classifier分类器
ASGD就是用空间换时间的一种SGD (随机梯度下降)
SAG(随机平均梯度)
SAG是在SGD基础上的改进。顾名思义,它也和SGD一祥、每次取随随机的 个样本计算 梯度,但不同的是,它是用所有样本梯度的平均值来更新参数。
4.4.4 案例:癌症分类预测-良/恶性乳腺癌肿瘤预测
-
数据介绍
原始数据的下载地址:https://archive.ics.uci.edu/ml/machine-learning-databases/
数据:http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Original%29
文件链接:https://pan.baidu.com/s/1kkYUbbwwxnY13Ms–hX0fA?pwd=1024
提取码:1024
数据描述
(1)699条样本,共11列数据,第一列用语检索的id,后9列分别是与肿瘤
相关的医学特征,最后一列表示肿瘤类型的数值。
(2)包含16个缺失值,用”?”标出。
| Attribute | Domain |
|---|---|
| 1. Sample code number 样本编码数 | id number |
| 2. Clump Thickness 团块厚度 | 1 - 10 |
| 3. Uniformity of Cell Size 细胞大小均匀性 | 1 - 10 |
| 4. Uniformity of Cell Shape 细胞形状均匀性 | 1 - 10 |
| 5. Marginal Adhesion 边缘粘连性 | 1 - 10 |
| 6. Single Epithelial Cell Size 单个上皮细胞大小 | 1 - 10 |
| 7. Bare Nuclei 裸露核 | 1 - 10 |
| 8. Bland Chromatin 平滑染色质 | 1 - 10 |
| 9. Normal Nucleoli 正常核仁 | 1 - 10 |
| 10. Mitoses 有丝分裂 | 1 - 10 |
| 11. Class: 类别 | (2 for benign, 4 for malignant) (2为良性,4为恶性) |
分析
流程分析:
1)获取数据
读取的时候加上names
2)数据处理
处理缺失值
3)数据集划分
4)特征工程:
无量纲化处理-标准化
5)逻辑回归预估器
6)模型评估
代码
因为我们要读取数据,所以我们用jupyter来做。
import pandas as pd
import numpy as np
# 1.读取数据
column_name = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
'Normal Nucleoli', 'Mitoses', 'Class']
# data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
# names=column_name)
data = pd.read_csv("./breast+cancer+wisconsin+original/breast-cancer-wisconsin.data",
names=column_name)
data
# 2.缺失值处理
# 1)?替换成np.nan
data = data.replace(to_replace="?", value=np.nan)
# 2)删除缺失样本
data.dropna(inplace=True)# 默认按行删除 inplace:True 修改原数据,False 返回新数据,默认 False
data.isnull()# 判断是否有 NaN
data.isnull().any() # 不存在缺失值了
data
# 3. 划分数据集
from sklearn.model_selection import train_test_split
# 筛选特征值和目标值
x = data.iloc[:,1:-1]
y = data["Class"] # y = data.iloc[:,-1]
x.head()
y.head()
x_train,x_test,y_train,y_test = train_test_split( x, y )
# test_size 测试集的大小 默认0.25 ,random_state 随机数种子, 根据你的需求去设置吧,我们在这里不需要
x_train
# 4.特征工程-标准化
from sklearn.preprocessing import StandardScaler
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
x_train
# 5.预估器流程:使用逻辑回归
from sklearn.linear_model import LogisticRegression
estimator = LogisticRegression()
estimator.fit(x_train,y_train)
# 逻辑回归的模型参数;回归系数和偏置
estimator.coef_
estimator.intercept_
# 6.模型评估
# 方法1: 直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接对比真实值和预测值:\n",y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test,y_test)
print("准确率为:",score)
y_predict:
[4 2 4 2 4 2 2 4 2 2 4 4 2 2 2 2 4 2 2 4 4 2 4 4 2 2 2 2 2 2 2 4 2 4 2 2 2
2 4 4 2 2 2 4 4 2 2 2 4 4 4 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 4 2 2 2 4 4 2 4
2 2 2 4 4 2 2 2 4 4 2 4 2 2 4 2 2 2 2 2 2 2 4 2 4 2 4 4 2 2 4 4 2 2 2 2 4
2 4 2 2 2 2 2 4 4 4 4 2 2 2 4 4 2 4 4 4 2 4 2 2 2 2 2 4 2 2 2 4 2 4 2 4 2
2 4 2 2 2 2 2 4 2 2 2 2 4 4 2 2 2 2 4 2 2 2 2]
直接对比真实值和预测值:
349 True
685 True
255 True
370 True
359 True
...
251 True
115 True
675 True
387 True
332 True
Name: Class, Length: 171, dtype: bool
准确率为: 0.9766081871345029
在很多分类场景当中我们不一定只关注预测的准确率!!!!!
比如以这个癌症举例子!!!我们并不关注预测的准确率,而是关注在所有的样本当中,癌症患者有没有被全部预测(检测)出来。
真的患癌症的,能够被检查出来的概率 - 召回率
4.4.5 分类的评估方法
1、精确率与召回率
混淆矩阵
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵(适用于多分类)
TP:True Possitive
FN : False Negative
精确率(Precision)与召回率(Recall)
精确率:预测结果为正例样本中真实为正例的比例(了解)
TP / (TP+FP)
召回率:真实为正例的样本中预测结果为正例的比例(查的全不全,对正样本的区分能力)
TP / (TP+FP)
如果说我们因为要预测癌症或者良性或恶性的时候,我们一般把 恶性 作为我们的 正例 ,因为我们更关注谁患了癌症,所以恶性是正例,所以我们看真实有恶性肿瘤的,那么真正被预测为恶性肿瘤的是不是就是我们更关注的一个指标呀,那所以我们这个召回率是不是就是我们刚刚说的这个真的患癌症的能够被检查出来的概率,其实是什么呀? 召回率,就是看你查的全不全,是一种对样本的区分能力。
那么怎么更好理解这个两个概念
还有其他的评估标准,F1-score,反映了模型的稳健型
等价于 ==> 2 * 精确率 * 召回率 / (精确率 + 召回率)
F1- score如果值大的话,那么就意味着,我们这个不仅精确率高,这个召回率也很高,这样就保证了模型的稳健性。
分类评估报告API
- sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
- y_true:真实目标值
- y_pred:估计器预测目标值
- labels:指定类别对应的数字
- target_names:目标类别名称
- return:每个类别精确率与召回率
这样的话,我们是不是可以去看一下我们癌症案例预测出来的结果,这个模型它的精确率、召回率和F1- score 是怎么样的一个情况
代码:
# 查看精确率、召回率、F1-score
from sklearn.metrics import classification_report
report = classification_report(y_test,y_predict,labels=[2,4],target_names=['良性','恶性'])
print(report)
precision 准确率
recall 召回率
f1-score 模型的稳健型
support 样本量
其实我们可以看到,我们最关注的是 recall 召回率,恶性肿瘤的召回率是0.94,如果有一百个人患有恶性肿瘤的话,只有94个被查出来了,那还有6个怎么办呀,这个问题就很严峻了。
召回率应用场景除了癌症预测还有例如工厂 质量检测,查次品 也是比较关注的是 召回率。
假设这样一个情况,总共有100个人,如果99个样本癌症,1个样本非癌症,不管怎样我全都预测正例(默认癌症为正例), 准确率就为99%,但是这样效果并不好,这就是样本不均衡下的评估问题
总共有100个人,如果99个样本癌症,1个样本非癌症 - 样本不均衡
不管怎样我全都预测正例(默认癌症为正例) - 不负责任的模型
准确率:99%
召回率:99/99 = 100%
精确率:99%
F1-score: (2*99%*100%) / (99%+100%) = 2*99% / 199% = 99.497%
AUC:0.5
TPR = 100%
FPR = 1 / 1 = 100%
问题:如何衡量样本不均衡下的评估? ROC曲线与AUC指标
2、ROC曲线与AUC指标
知道TPR与FPR
- TPR = TP / (TP + FN)
- 所有真实类别为1的样本中,预测类别为1的比例
- 召回率
- FPR = FP / (FP + FN)
- 所有真实类别为0的样本中,预测类别为1的比例
ROC曲线
- ROC曲线的横轴就是FPRate,纵轴就是TPRate,当二者相等时,表示的意义则是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的,TPR = FPR ,ROC曲线就是这个红色虚线,此时AUC为0.5(三角形面积1*1/2)
ROC曲线就是这条蓝线,AUC指标就是这张图当中曲线和x轴y轴包成的这个区域的面积。
AUC指标
- AUC的概率意义是随机取一对正负样本,正样本得分大于负样本的概率
- AUC的最小值为0.5,最大值为1,取值越高越好
- AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- 如果AUC<0.5,我们这个时候叫做反向预测,我们把它反过来预测就准了(反着看)
最终AUC的范围在[0.5, 1]之间,并且越接近1越好
AUC计算API
- from sklearn.metrics import roc_auc_score
- sklearn.metrics.roc_auc_score(y_true, y_score)
- 计算ROC曲线面积,即AUC值
- y_true:每个样本的真实类别,必须为0(反例),1(正例)标记
- y_score:预测得分,可以是正类的估计概率、置信值或者分类器方法的返回值。
- sklearn.metrics.roc_auc_score(y_true, y_score)
# 每个样本的真实类别,必须为0(反例),1(正例)标记
# 将y_test 转换成 0 1
y_true = np.where(y_test>3, 1, 0)
y_true
from sklearn.metrics import roc_auc_score
roc_auc_score(y_true,y_predict)# AUC指标
总结
- AUC只能用来评价二分类
- AUC非常适合评价样本不平衡中的分类器性能
4.5 模型保存和加载
当训练或者计算好一个模型之后,那么如果别人需要我们提供结果预测,就需要保存模型(主要是保存算法的参数)
sklearn模型的保存和加载API
- from sklearn.externals import joblib 或者 import joblib
- 保存:joblib.dump(estimator , ‘test.pkl’)
- 加载:estimator = joblib.load(‘test.pkl’)
线性回归的模型保存加载案例
- 保存
import joblib
# 保存模型
joblib.dump(estimator,"./my_ridge.pkl")
- 加载
# 加载模型
estimator = joblib.load("my_ridge.pkl")
报错ImportError: cannot import name ‘joblib’ from ‘sklearn.externals’
解决办法1: 在终端中下载0.21.0之前版本的sklearn
pip install sklearn==0.20.4
解决办法2: 不用更改sklearn的版本号,直接在代码中使用import joblib即可
4.6 无监督学习-K-means算法
回忆非监督学习的特点?
没有目标值 - 无监督学习
4.6.1 什么是无监督学习
- 一家广告平台需要根据相似的人口学特征和购买习惯将美国人口分成不同的小组,以便广告客户可以通过有关联的广告接触到他们的目标客户。
- Airbnb 需要将自己的房屋清单分组成不同的社区,以便用户能更轻松地查阅这些清单。
- 一个数据科学团队需要降低一个大型数据集的维度的数量,以便简化建模和降低文件大小。
我们可以怎样最有用地对其进行归纳和分组?我们可以怎样以一种压缩格式有效地表征数据?这都是无监督学习的目标,之所以称之为无监督,是因为这是从无标签的数据开始学习的。
4.6.2 无监督学习包含算法
- 聚类
- K-means(K均值聚类)
- 降维
- PCA
4.6.3 K-means原理
我们先来看一下一个K-means的聚类效果图
K-means聚类步骤
- 随机设置K个特征空间内的点作为初始的聚类中心。
- K就是K-means的K
- K-超参数(超参数就是得人手动指定的参数)
- 看需求
- 调节超参数
- 对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 中心点怎么求?
A(a1, b1, c1)
B(a2, b2, c2)
……
Z(a26,b26,c26)
中心点(a平均,b平均,c平均)
- 中心点怎么求?
- 如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程
我们以一张图来解释效果
4.6.4 K-meansAPI
- sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
cluster一簇,一串- k-means聚类
- n_clusters: 开始的聚类中心数量
- init: 初始化方法,默认为’k-means ++’,其实就是一种对k-means的一种优化方法
- 属性
- labels_: 默认标记的类型,可以和真实值比较(不是值比较)
4.6.5 案例:k-means对Instacart Market用户聚类
分析
1、降维之后的数据
2、k-means聚类
3、聚类结果显示
k = 3
流程分析:
降维之后的数据
1)预估器流程
2)看结果
3)模型评估
代码
# 1)预估器流程
from sklearn.cluster import KMeans
estimator = KMeans(n_clusters=3)
estimator.fit(data_new)
y_predict = estimator.predict(data_new)
y_predict[:300]
问题:如何去评估聚类的效果呢?
4.6.6 Kmeans性能评估指标
轮廓系数
注:对于每个点i 为已聚类数据中的样本 ,b_i 为i 到其它族群的所有样本的距离最小值,a_i 为i 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值
轮廓系数值分析
高内聚,低耦合
- 分析过程(我们以一个蓝1点为例)
- 1、计算出蓝1离本身族群所有点的距离的平均值a_i
- 2、蓝1到其它两个族群的距离计算出平均值红平均,绿平均,取最小的那个距离作为b_i
- 根据公式:极端值考虑:如果b_i >>a_i: 外部距离很大,内部距离很小,那么公式结果趋近于1;如果a_i>>b_i: 那么公式结果趋近于-1
>> 远远大于
结论
如果b_i>>a_i:趋近于1效果越好, b_i<<a_i:趋近于-1,效果不好。轮廓系数的值是介于 [-1,1] ,越趋近于1代表内聚度和分离度都相对较优。
轮廓系数API
- sklearn.metrics.silhouette_score(X, labels)
- 计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值
用户聚类结果评估
# 模型评估 - 轮廓系数
from sklearn.metrics import silhouette_score
silhouette_score(data_new,y_predict)
4.6.7 K-means总结
- 特点分析:采用迭代式算法,直观易懂并且非常实用
- 缺点:容易收敛到局部最优解(多次聚类)
如果K-means聚类步骤一(随机设置K个特征空间内的点作为初始的聚类中心)如果一开始设置的点都堆在一起,这样就会导致我们的结果容易陷入到局部最优,可能都会挤在一起,我们需要避免这种情况,怎么避免?其中一个方法就是可以通过 多次聚类,多随机取一下聚类中心是可以避免这个问题的。 - 应用场景:
- 没有目标值
- 分类
注意:聚类一般做在分类之前,如果我们一开始没有目标值的话,第一次我们会先做一个聚类,在之后我们会有新的用户数据或者一些其他的应用场景 那我们就可以根据之前聚好的类然后进行分类了