前言

深度优先搜索（DFS）和广度优先搜索（BFS）是图论中两个非常重要的算法，主要用于拓扑排序，寻路（走迷宫）和搜索引擎等。在我们写算法时经常会遇到需要使用DFS和BFS的题目，例如leetcode中的岛屿相关的问题以及有关树的题目大多都会使用DFS或者BFS。

深度优先搜索和广度优先搜索简介

深度优先搜索

深度优先搜索的遍历过程：
1.从图中一个未被访问的顶点v开始
2.沿着一条路走到底
3.当无路可走时，开始回退到上一个节点走另一条路走到底，重复2-3
4.一直执行3，直到走完所有节点
5.深度优先搜索的特点：不撞南墙不回头。

图解🖼

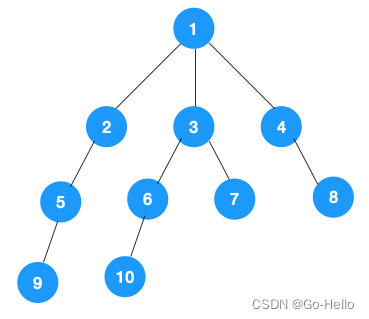
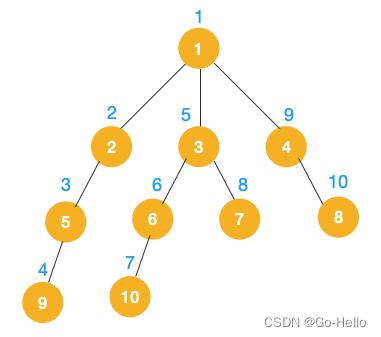
这里以树为例

我们从上面的步骤开始走：

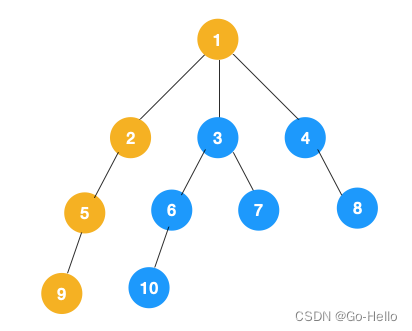
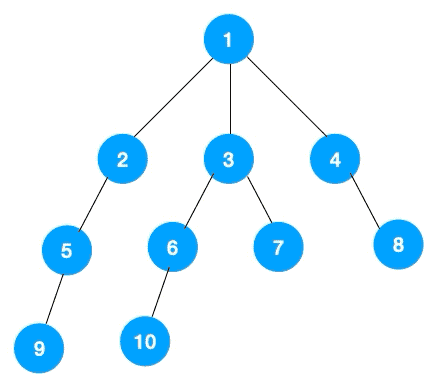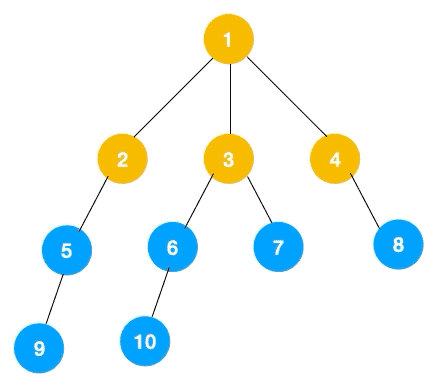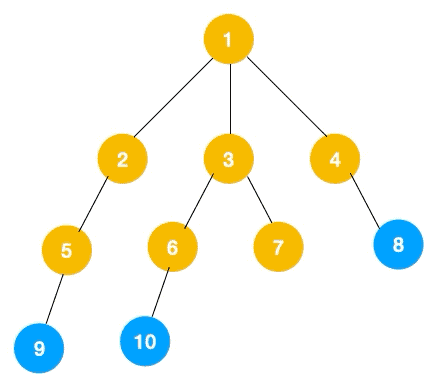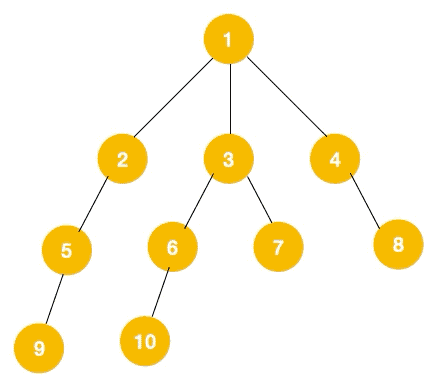
1.从根节点1开始遍历，与它相邻的节点有2、3、4，我们先遍历2节点，再遍历2的子节点5，然后再遍历5的子节点9。

2.可以看到第一条路已经走到底了，所以我们开始回退，但是5点和2节点并没有其他路可以走，直到回退到1节点才有除了2以外的节点3、4，我们继续重复步骤一遍历3节点。

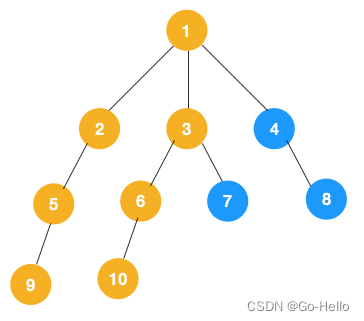
3.同理从 10 开始往上回溯到 6, 6 没有除 10 以外的子节点，再往上回溯，发现 3 有除 6 以外的子点 7，所以此时会遍历 7

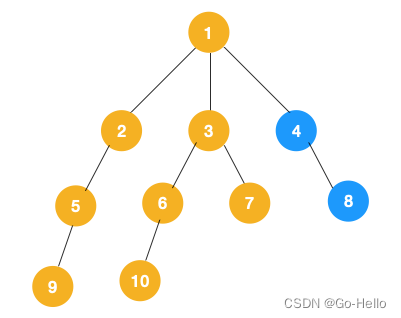
4.从 7 往上回溯到 3， 1，发现 1 还有节点 4 未遍历，所以此时沿着 4， 8 进行遍历,这样就遍历完成了

相信大家看到以上的遍历不难发现这就是树的前序遍历,实际上不管是前序遍历，还是中序遍历，亦或是后序遍历，都属于深度优先搜索。那么深度优先搜索是怎么实现的呢，深度优先搜索有递归和非递归两种实现方式。

代码实现

递归实现（这里以树的先序搜索为例）

递归实现比较简单且容易理解，由于是前序遍历，所以我们只需要依次遍历当前节点、左节点和右节点即可，对于左节点再依次遍历他们的右节点即可。依次遍历下去，直到叶子节点（终止条件）。
代码如下：

  type TreeNode struct {
      Val int
      Left *TreeNode
      Right *TreeNode
  }
  func preorderTraversal(root *TreeNode) (vals []int) {
    var preorder func(*TreeNode)
    preorder = func(node *TreeNode) {
        if node == nil {
            return
        }
        vals = append(vals, node.Val)
        preorder(node.Left)
        preorder(node.Right)
    }
    preorder(root)
    return
}

递归的表达性很好，也很容易理解，不过如果层级过深，很容易导致栈溢出。接下来我们看一下非递归实现。

非递归实现

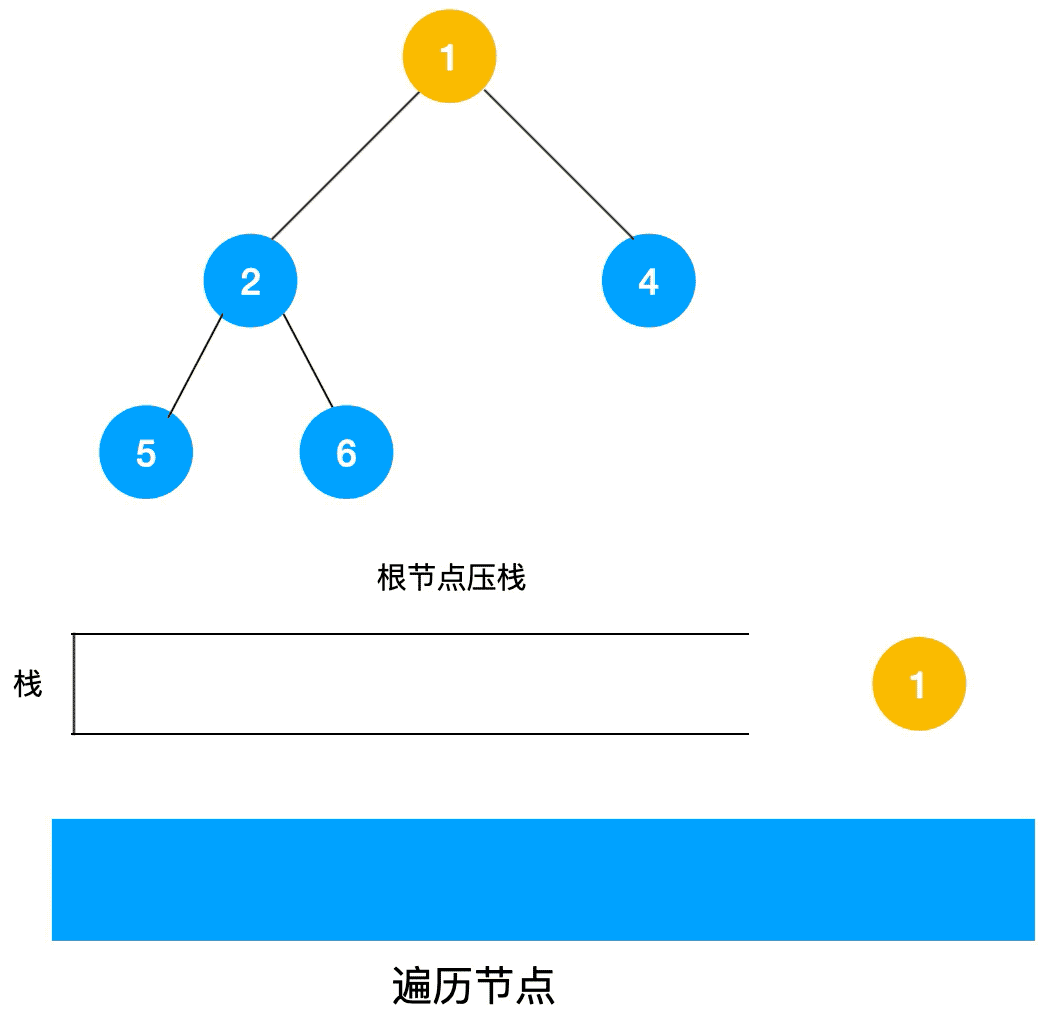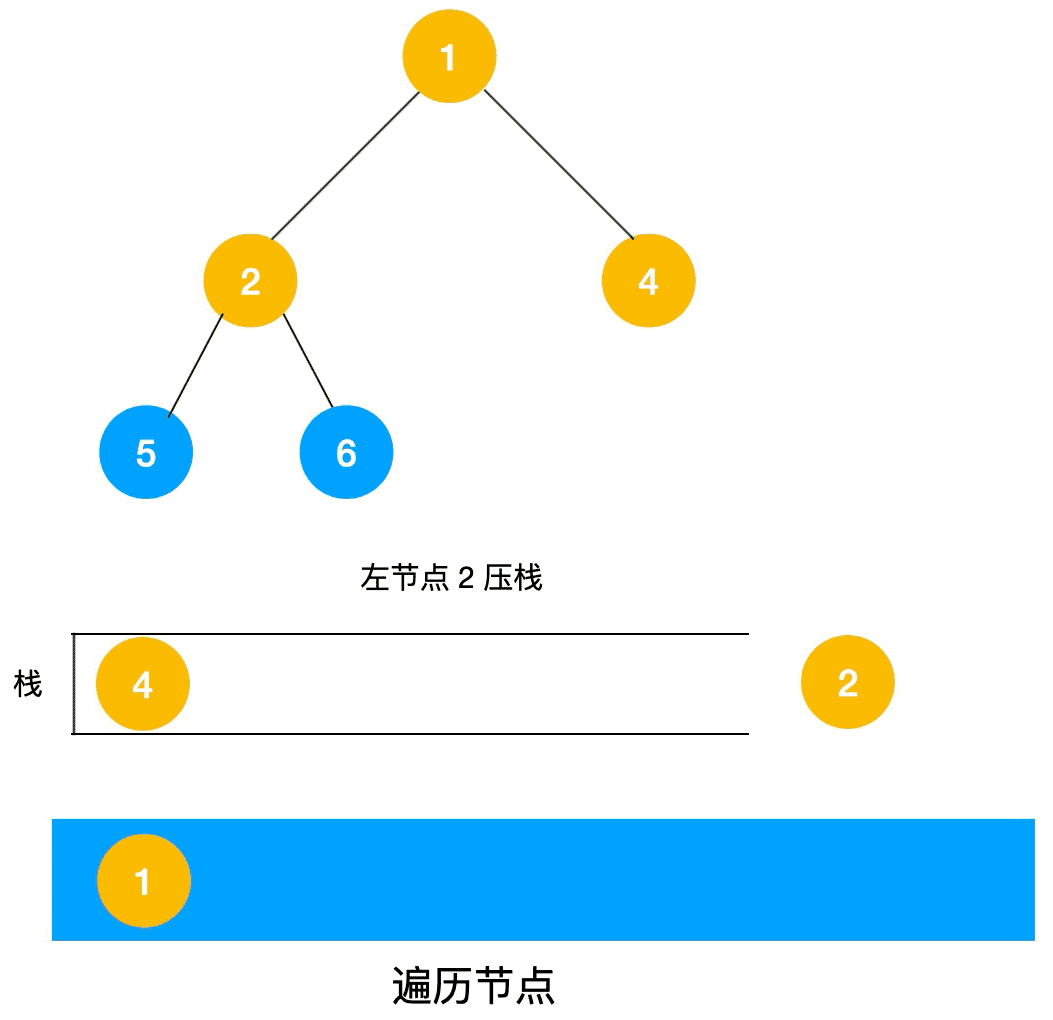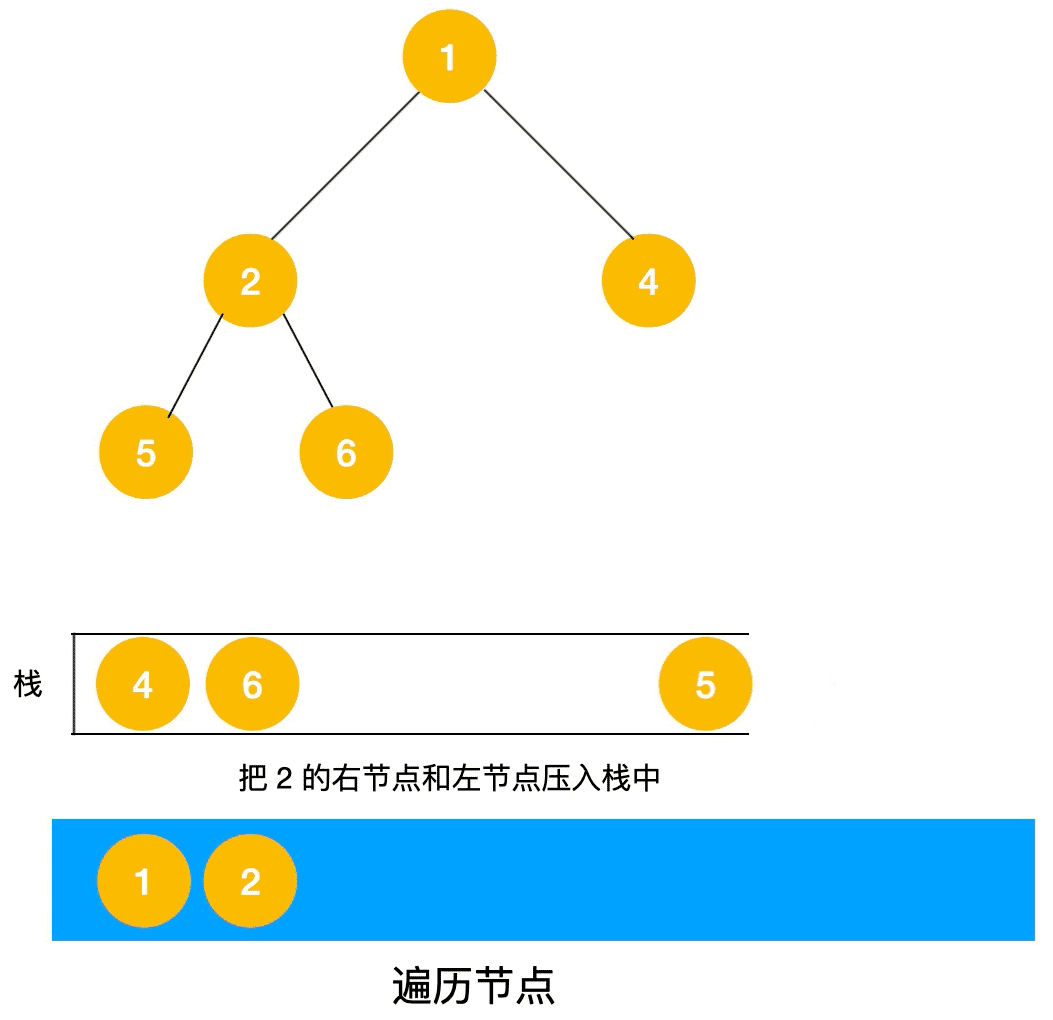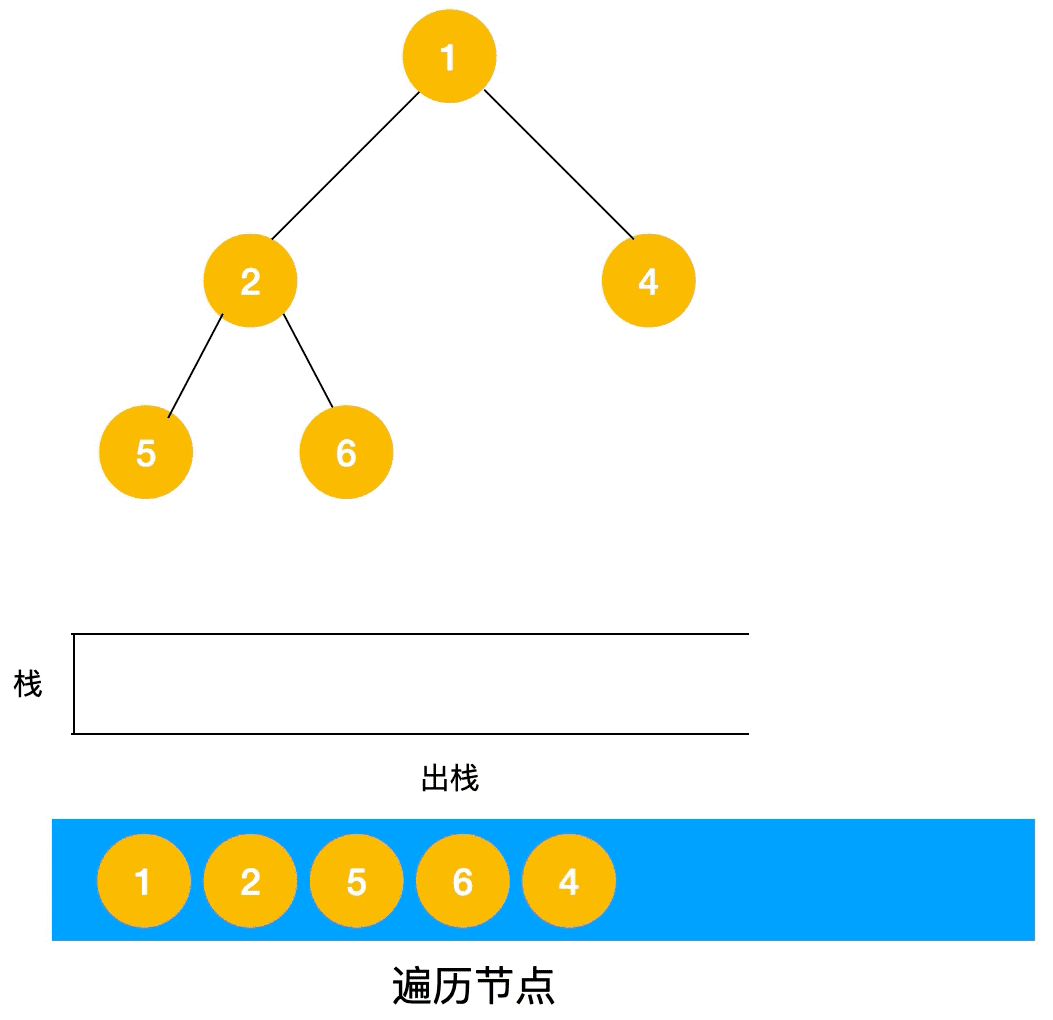
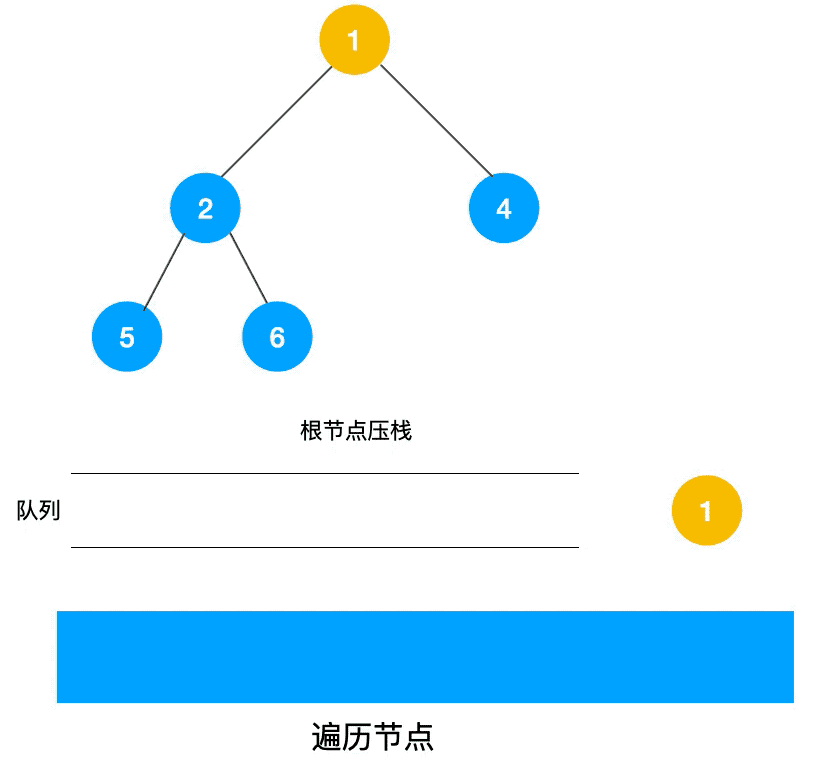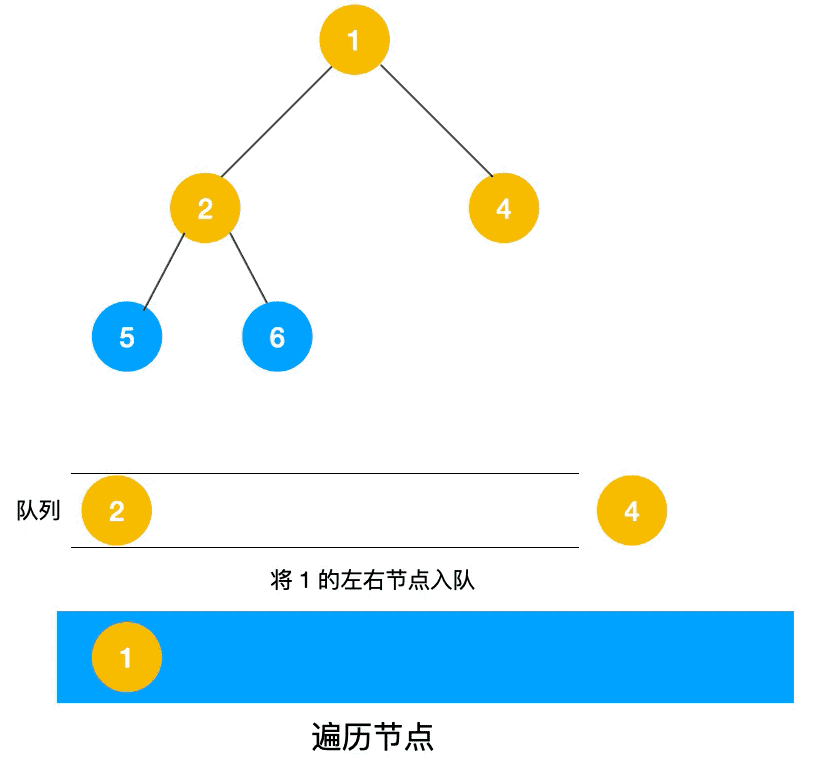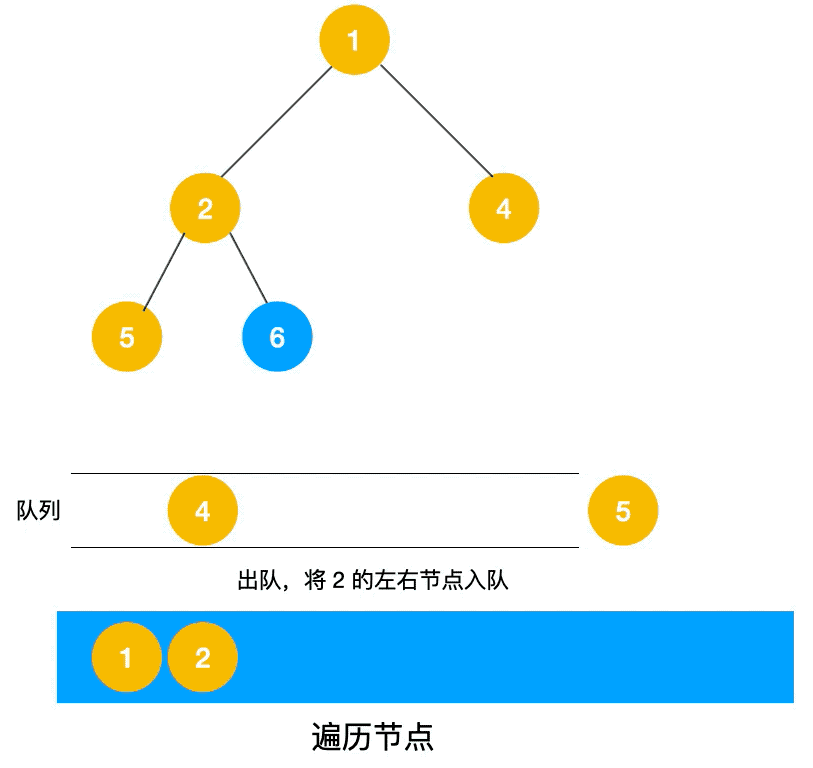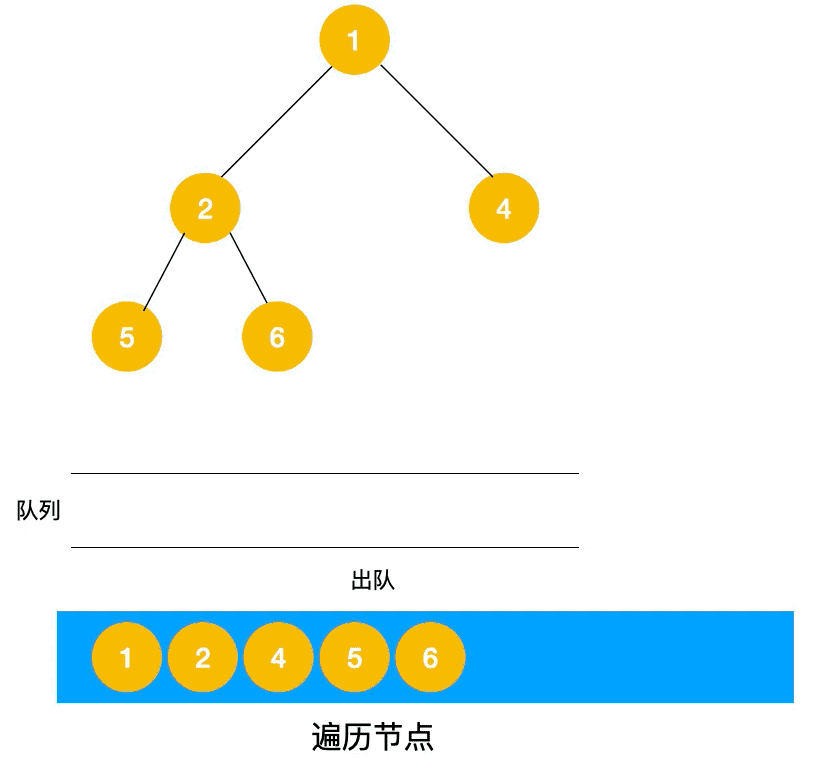
深度优先搜索的非递归实现是通过栈来实现的，由于是先序遍历，所以我们先遍历当前节点，然后把右节点压栈，再压左节点（这样弹栈的时候会先拿到左节点遍历，符合深度优先遍历要求）弹栈，拿到栈顶的节点，如果节点不为空，重复步骤 ， 如果为空，结束遍历。
我们先看一下实现过程图🖼：

最后我们看一下代码实现

type TreeNode struct {
      Val int
      Left *TreeNode
      Right *TreeNode
	}
func preorderTraversal(root *TreeNode) []int {
    var res []int
    if root == nil {
        return res
    }
    var stack []*TreeNode
    stack = append(stack, root)
    for len(stack) > 0 {
        size := len(stack)
        temp := stack[size - 1]
        if size <= 1 {
            stack = []*TreeNode{}
        } else {
            stack = stack[: size - 1]
        }
        res = append(res, temp.Val)
        if temp.Right != nil {
            stack = append(stack, temp.Right)
        }
        if temp.Left != nil {
            stack = append(stack, temp.Left)
        }
    }
    return res

}

广度优先搜索（BFS）

与深度优先搜索不同，广度优先搜索是从图中未遍历的节点出发，先遍历该节点的相邻节点，再依次遍历每个相邻节点的相邻节点。

图解🖼

我们依旧以树为例：
广度优先搜索也叫层序遍历，先遍历第一层（节点 1），再遍历第二层（节点 2，3，4），第三层（5，6，7，8），第四层（9，10）。

看完图解，我们来看一下BFS的实现方式：
上文我们提到了DFS的非递归实现方式，主要是运用了栈，那么我们是否也能通过栈来实现广度优先搜索呢，很显然是不行的，那么我们就需要用到另外一种数据结构队列（queue）。接下来我们看一下队列实现BFS的动态过程。

了解了遍历过程之后，我们来看一下BFS的代码实现；

代码实现

type TreeNode struct {
      Val int
      Left *TreeNode
      Right *TreeNode
	}
func bfs(root *TreeNode) [][]int {
    res:=[][]int{}
    if root==nil{//防止为空
        return res
    }
    queue:=list.New()
    queue.PushBack(root)
    var tmpArr []int
    for queue.Len()>0 {
        length:=queue.Len()//保存当前层的长度，然后处理当前层（十分重要，防止添加下层元素影响判断层中元素的个数）
        for i:=0;i<length;i++{
            node:=queue.Remove(queue.Front()).(*TreeNode)//出队列
            if node.Left!=nil{
                queue.PushBack(node.Left)
            }
            if node.Right!=nil{
                queue.PushBack(node.Right)
            }
            tmpArr=append(tmpArr,node.Val)//将值加入本层切片中
        }
        res=append(res,tmpArr)//放入结果集
        tmpArr=[]int{}//清空层的数据
    }
    return res
}

最后附上一道比较经典的BFS、DFS算法题
leetcode 200.岛屿数量
这里附上两种方法的代码实现：
DFS

func numIslands(grid [][]byte) int {
	count := 0
	for i := 0; i < len(grid); i++ {
		for j := 0; j < len(grid[0]); j++ {
			if grid[i][j] == '1' {
				dfs(grid, i, j)
				count++
			}
		}
	}
	return count
}
func dfs(grid [][]byte, i, j int) {
	if i < 0 || j < 0 || i >= len(grid) || j >= len(grid[0]) || grid[i][j] != '1' {
		return
	}
	grid[i][j] = '2'//避免重复遍历
	dfs(grid, i+1, j)
	dfs(grid, i-1, j)
	dfs(grid, i, j+1)
	dfs(grid, i, j-1)
}

BFS

func numIslands(grid [][]byte) int {
	count :=0
    optionX:=[]int{-1,0,0,1}
    optionY:=[]int{0,1,-1,0}
    queue :=[][]int{}
    for i:=0;i<len(grid);i++{
        for j:=0;j<len(grid[0]);j++{
            if grid[i][j]=='1'{
                count++
                queue = append(queue,[]int{i,j})
                grid[i][j]='2'//避免重复遍历
                for len(queue)!=0{
                    u :=queue[0]
                    queue = queue[1:]
                    for m :=0;m<4;m++{
                        newX := u[0]+optionX[m]
                        newY := u[1]+optionY[m]
                        if newX>=0&&newY>=0&&newX<len(grid)&&newY<len(grid[0])&&grid[newX][newY]=='1'{
                            queue = append(queue,[]int{newX,newY})
                            grid[newX][newY]='2'//同理，避免重复遍历
                        }
                    }
                }
            }
        }
    }
    return count
}