数据结构与算法学习笔记----树与图的深度优先遍历
@@ author: 明月清了个风
@@ first publish time: 2024.12.9
pa⭐️这里只有一道题哈哈。
Acwing 846.树的重心
给定一棵树,树中包含
n
n
n个节点(编号
1
∼
n
1 \sim n
1∼n)和
n
−
1
n - 1
n−1条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数
n
n
n,表示树的节点数。
接下来
n
−
1
n - 1
n−1行,每行包含两个整数
a
a
a和
b
b
b,表示点
a
a
a和
b
b
b之间存在一条边。
输出格式
输出一个整数 m m m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例
4
思路
首先是建树,使用的还是邻接表的方式,这个在哈希表中讲过了,如果不太懂可以去看一下,这题中的注意点就是因为是无向边,所以存的边数需要乘两倍
为什么用dfs:根据题意,我们需要在树中找到重心,而重心会将树划分为不同的连通块,我们需要统计的是不同连通块中点的数目,因此可以考虑dfs,这里大家可能会说为什么不是bfs,其实也可以,但是相对来说,bfs更强调点与点之间层级的概念,而这里我们只需要统计即可,因此dfs可能更加合适。
-
现在以输入样例中的树的形状为例解释一下题意(这里提前告诉大家重心是
1号点):我们从
1号点开始dfs(在这题里面其实从存在点开始就行,哪个点不重要,以后会碰到有些题对起始点也有考虑的)。根据题意我们将
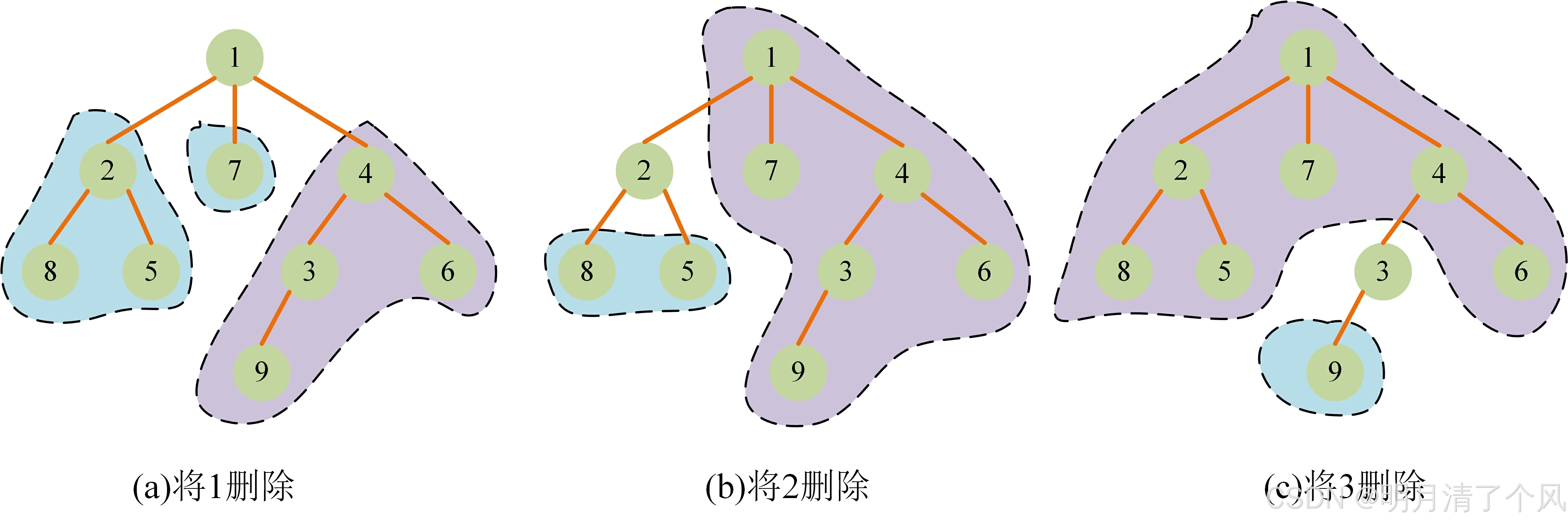
1号点删除后,会将树分为 3 3 3个连通块,如图所示,那么对于1号点来说,剩余连通块中点数的最大值就是4(图中紫色背景的连通块);将
2号点删除后,会将树分为 2 2 2个连通块,那么对于2号点来说,剩余连通块中点数的最大值就是6(图中紫色背景的连通块);以此类推…(需要注意的是这并不是dfs的顺序,只是用来说明题意)
-
代码思路
既然已经考虑使用dfs进行解决,那么就要考虑dfs中具体需要维护的内容了。
-
首先最基本的就是连通块中点的统计,这很简单,伪代码如下
以上面的图(a)距离来说,我们
dfs(1)后,会在for循环中找到三个点2, 7, 4,这里就以2举例,那么对于2来说,我们会搜到他能到的点是1, 8, 5,但是我们是从1过来的,标记了st[1] = true,因此不会往回走了(这里是一个重点,后面会重新提到),所以dfs(2)中的for循环只会遍历到8, 5,那么对于这两个点也是同样的情况,不会往回走,但是他们的for中没有别的点可以走了,因此就是直接返回sum + 1 = 0 + 1 = 1。int dfs(int u) { st[u] = true; // 标记这个点搜过了 int sum = 0; // 记录以这个点所在连通块的点的总数 for(int i = h[u]; i != -1; i = ne[i]) // 连通块的遍历 { int j = e[i]; // 取出u通向的点 if(st[j]) continue; // 判断这个点搜过了没有 int s = dfs(j); // 递归搜j点所在连通块的点的总数,因为这个连通块中搜过的点都会被标记,所以不会重复搜 sum += s; // 加上递归搜到的总数, } return sum + 1; } -
然后是删除该点后连通块的最大值的维护
因为我们的dfs返回的是该点所在连通块中点的总数,但是我们需要维护的是删除该点后,剩下几个连通块中点数的最大值,也就是不包含这一点,因此这个量我们需要在
for循环中维护,因为for循环中,我们会遍历所有当前点能去到的点并统计其所在连通块的点数int s =dfs(j),这就相当于将u点删除后,他分割出的一个连通块的点的总数,因此只需要对这个量取最大值即可,增加一个量size进行维护size = max(size, s),代码修改如下:int dfs(int u) { st[u] = true; // 标记这个点搜过了 int size = 0; // 记录删除当前点u后分割出的连通块的点数的最大值 int sum = 0; // 记录以这个点所在连通块的点的总数 for(int i = h[u]; i != -1; i = ne[i]) // 连通块的遍历 { int j = e[i]; // 取出u通向的点 if(st[j]) continue; // 判断这个点搜过了没有 int s = dfs(j); // 递归搜j点所在连通块的点的总数,因为这个连通块中搜过的点都会被标记,所以不会重复搜 size = max(size, s); sum += s; // 加上递归搜到的总数, } return sum + 1; } -
最后就是所有剩下连通块的点数的最大值的最小值
在上述dfs过程中,我们就可以维护出删除每个点后分割出的连通块的点数的最大值,要求最小值只需要用一个全局变量
ans进行维护就行,这里的一个注意点就是在上面第一点蓝字中提到的重点。还是以点2为例子,我们在第一层dfs(1)中已经将st[1] = true标记了,但是根据树的重心的定义,删除点2后,图(b)中紫色背景部分同样也是一个连通块,但是因为1被标记了所以在dfs(2)的for中不会向1走,那么1所在连通块的点数如何处理呢,这同样有可能改变最后size维护的大小,我们需要在for循环后加一步更新操作size = max(size, n - sum - 1);,已知当前点所在连通块的数量(包含当前点)是我们的返回值sum + 1,那么所有点减去这个量n - sum - 1,就是往回走的剩下那个连通块的点的数量,这里再和for循环中维护的size取个最大值就能保证没有遗漏了。
-
代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int n;
int h[N], e[N * 2], ne[N * 2], idx; // 无向边,因此要存两倍的量,节点数不用两倍
bool st[N]; // flag数组,标记每个点是否被dfs过
int ans = N; // 要求的值是最小值,因此答案初始化为最大值
void add(int a, int b) // 单链表的加边操作
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u) // dfs的返回值是dfs的这个点所在连通块的点的总数
{
st[u] = true; // 标记这个点被搜过了
// size表示删除这个点的话,剩余每个连通块中包含点数最大值,因此初始化为0
// sum表示当前dfs的点所在连通块的点的总数(不包含当前点),因此最后返回的是sum + 1
int size = 0, sum = 0;
for(int i = h[u]; i != -1; i = ne[i]) // 遍历这个点能去到的所有的点,dfs后就能找到他们所在连通块的点的最大值(存在size里了)
{
int j = e[i];
if(st[j]) continue; // 判断点有没有被搜过
int s = dfs(j); // s存的就是这个点所在连通块包含的点的总数,
size = max(size, s); // 找最大值
sum += s; // 加在当前dfs的点的总数里,也就是点u所在连通块的总的点数中
}
// 这里是个细节,因为我们是随便找一个点开始遍历,比如这里我们搜的是1,但是我们并不知道重心是谁
// 因此可能搜到后面的时候,往回走的点已经被搜过了,因此还要对比出去这个点的总数剩下的那个连通块的点的总数的大小,看图
size = max(size, n - sum - 1);
ans = min(ans, size);
return sum + 1;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1);
cout << ans << endl;
return 0;
}
1; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1);
cout << ans << endl;
return 0;
}