参考程序代码：

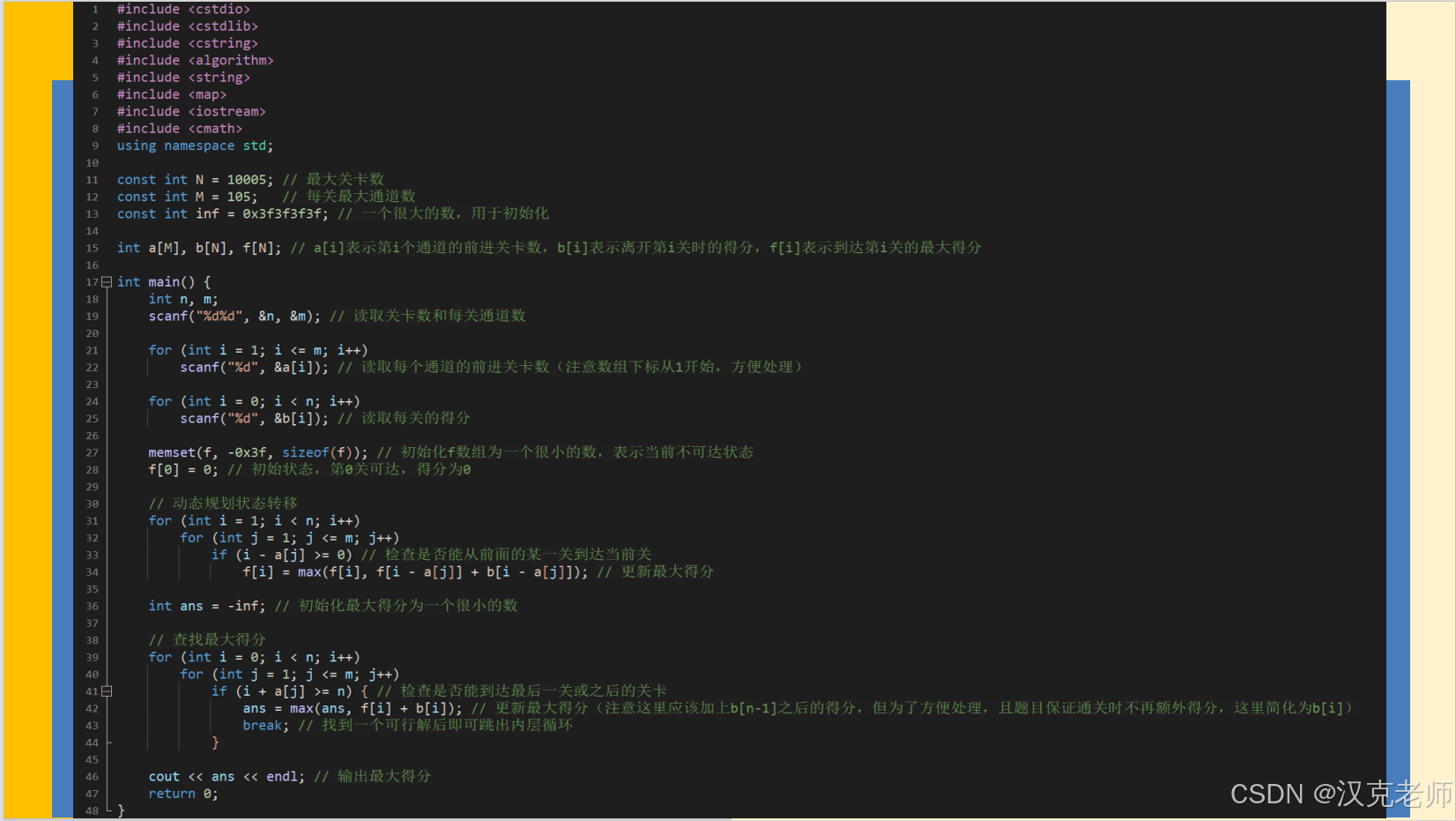
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <string>
#include <map>
#include <iostream>
#include <cmath>
using namespace std;

const int N = 10005; // 最大关卡数
const int M = 105;   // 每关最大通道数
const int inf = 0x3f3f3f3f; // 一个很大的数，用于初始化

int a[M], b[N], f[N]; // a[i]表示第i个通道的前进关卡数，b[i]表示离开第i关时的得分，f[i]表示到达第i关的最大得分

int main() {
    int n, m;
    scanf("%d%d", &n, &m); // 读取关卡数和每关通道数

    for (int i = 1; i <= m; i++)
        scanf("%d", &a[i]); // 读取每个通道的前进关卡数（注意数组下标从1开始，方便处理）

    for (int i = 0; i < n; i++)
        scanf("%d", &b[i]); // 读取每关的得分

    memset(f, -0x3f, sizeof(f)); // 初始化f数组为一个很小的数，表示当前不可达状态
    f[0] = 0; // 初始状态，第0关可达，得分为0

    // 动态规划状态转移
    for (int i = 1; i < n; i++)
        for (int j = 1; j <= m; j++)
            if (i - a[j] >= 0) // 检查是否能从前面的某一关到达当前关
                f[i] = max(f[i], f[i - a[j]] + b[i - a[j]]); // 更新最大得分

    int ans = -inf; // 初始化最大得分为一个很小的数

    // 查找最大得分
    for (int i = 0; i < n; i++)
        for (int j = 1; j <= m; j++)
            if (i + a[j] >= n) { // 检查是否能到达最后一关或之后的关卡
                ans = max(ans, f[i] + b[i]); // 更新最大得分（注意这里应该加上b[n-1]之后的得分，但为了方便处理，且题目保证通关时不再额外得分，这里简化为b[i]）
                break; // 找到一个可行解后即可跳出内层循环
            }

    cout << ans << endl; // 输出最大得分
    return 0;
}

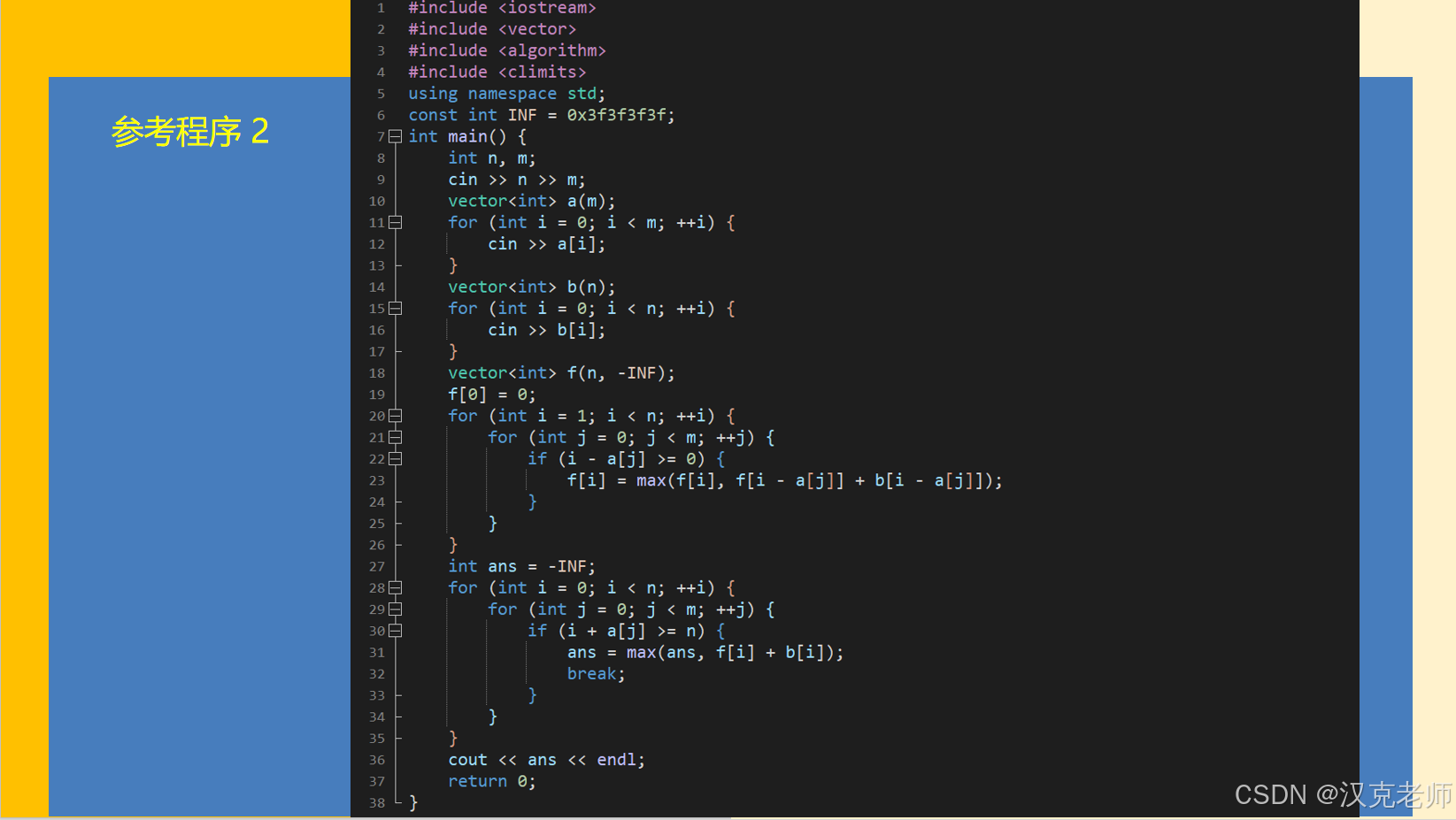
参考程序2代码：

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>

using namespace std;

const int INF = 0x3f3f3f3f;

int main() {
    int n, m;
    cin >> n >> m;

    vector<int> a(m); // 每个通道可以前进的关卡数
    for (int i = 0; i < m; ++i) {
        cin >> a[i];
    }

    vector<int> b(n); // 每关离开时获得的分数
    for (int i = 0; i < n; ++i) {
        cin >> b[i];
    }

    // f[i] 表示到达第 i 关时的最大分数
    vector<int> f(n, -INF);
    f[0] = 0; // 初始状态

    // 动态规划状态转移
    for (int i = 1; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (i - a[j] >= 0) {
                f[i] = max(f[i], f[i - a[j]] + b[i - a[j]]);
            }
        }
    }

    // 计算最终答案
    int ans = -INF;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (i + a[j] >= n) {
                ans = max(ans, f[i] + b[i]);
                break;
            }
        }
    }

    cout << ans << endl;

    return 0;
}