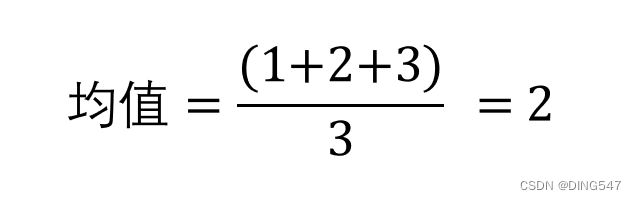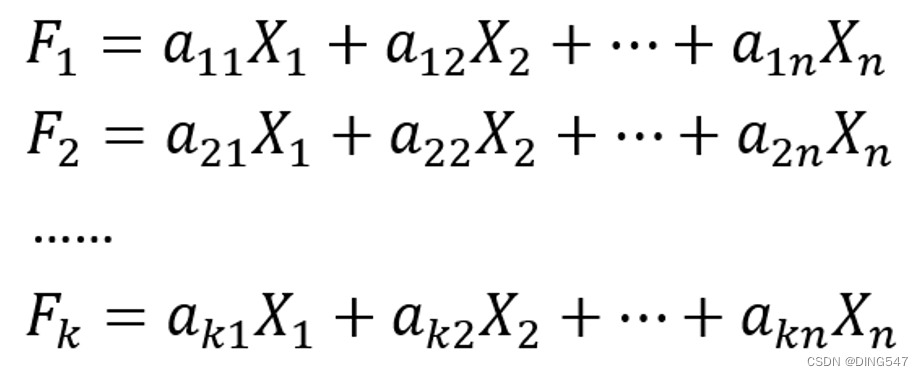目录
1、数据降维
降维的方法主要有两种:选择特征和抽取特征。选择特征即从原有的特征中挑选出最佳的特征,抽取特征即将数据由高维向低维投影,进行坐标的线性转换。PCA主成分分析即为典型的抽取特征的方法,它不仅是对高维数据降维,更重要的是经过降维去除噪声,发现数据中的模式。这一节主要介绍PCA主成分分析的基本原理,并通过简单案例来讲解如何通过Python来实现PCA主成分分析。
(1)PCA主成分分析原理介绍
1、二维空间降维
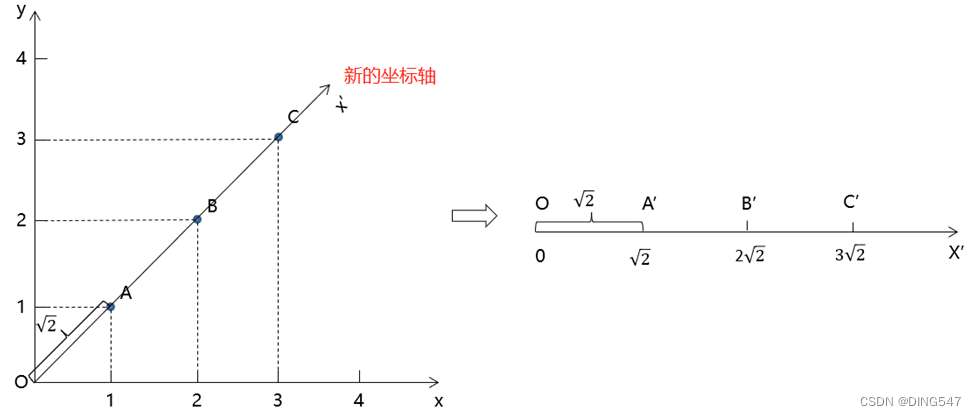
假设在二维坐标系上有一组数据,分别是A(1, 1),B(2, 2),C(3, 3),我们的目的就是把这一组二维数据转换为一维数据。
2、二维空间降维
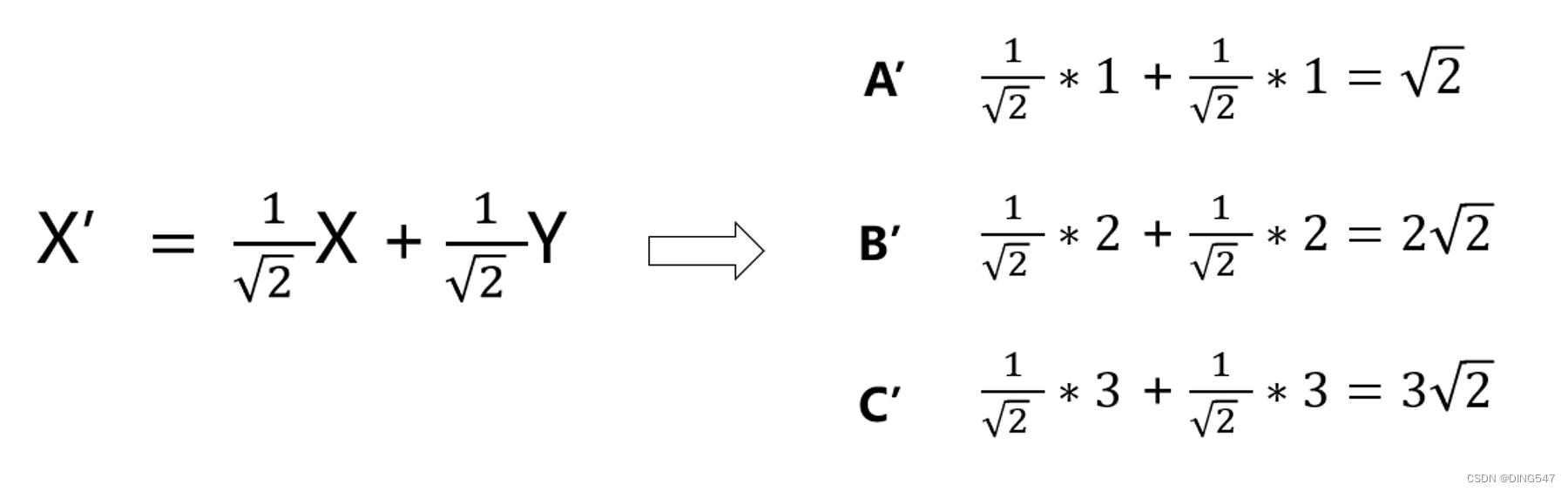
如果需要将这组数据从二维降至一维,我们可以将"y = x"这一条直线作为新的坐标轴,在下图右边新的坐标体系中,只有一条横轴x',而不再具有纵轴了,这样就把原来的二维数据转换为一维数据了,点A(1, 1)就变成了2√2这一个一维坐标了,点B(2, 2)就变成了2√2这个一维坐标了。
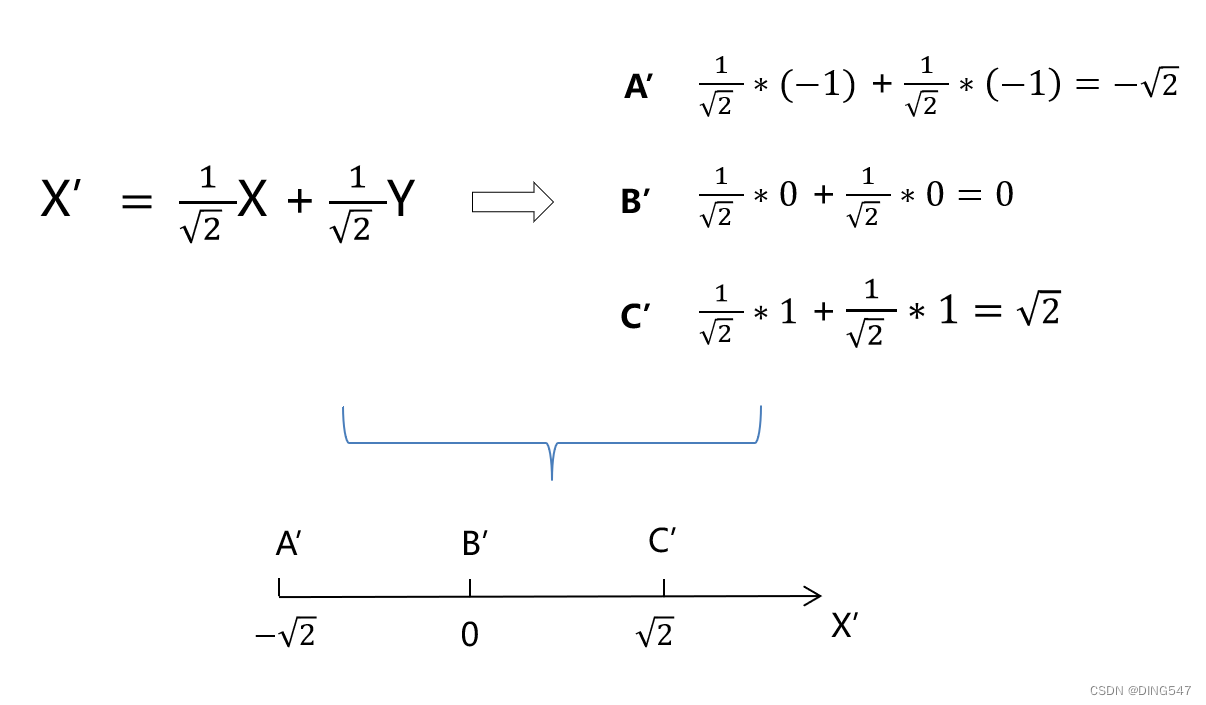
在实际进行数据降维前首先需要对特征数据零均值化,即对每个特征维度的数据减去该特征的均值。
对于二维到一维的数据降维,其本质就是在将原始数据零均值化后,寻找下图所示的合适的线性组合系数α和β,来将二维数据转换为一维数据。
3、n维空间降维
如果原特征变量有n个,那么就是n维空间降维,n维空间降维的思路和二维空间降维的思路是一致的。例如将n维数据(X1,X2,...,Xn )转换为一维数据,就是寻找下图所示的线性组合系数a1、a2……an:
在实际应用中,Python已经提供了相应的计算库供我们使用,能够快速地帮我们计算出这些系数。分析的是n维向量转成1维向量,那么如何n维向量(X1,X2,...,Xn )转成k维向量(F1,F2,…,Fk)呢,即将n个特征降维成k个新特征?只是从构造1个线性组合变为构造k个线性组合,如下图所示:
其中需要满足的线性代数条件如下所示,供感兴趣的读者参考:
(2) 各个主成分互不相关:
(3) 主成分的方差依次递减,重要性依次递减:
(2)PCA主成分分析代码实现
1、二维空间降维Python代码实现
使用PCA的python代码:
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[1, 1], [2, 2], [3, 3]])
pca = PCA(n_components=1)
pca.fit(X)
X_transformed = pca.transform(X) 降维后的结果X_transformed打印出来如下所示:
array([[-1.41421356],
[ 0. ],
[ 1.41421356]])提到数据降维其实是通过线性组合完成的,那么如何通过Python程序来获取线性组合中的系数呢,可以使用如下代码获得:
pca.components_ 将pca.components_打印出来,如下所示:
array([[0.70710678, 0.70710678]])2、三维空间降维Python代码实现
在根据已有的信用卡持有人信息及其违约数据来建立信用卡违约评判模型时,数据可能包含申请人的收入,年龄,性别,婚姻状况,工作单位等数百个维度的数据。此处为教学演示,我们选择年龄(岁),负债比率,月收入(元) 三个维度的数据使用PCA进行降维。
这里首先使用pandas库构建待降维的不同申请人的三维数据:
import pandas as pd
X = pd.DataFrame([[45, 0.8, 9120], [40, 0.12, 2600], [38, 0.09, 3042], [30, 0.04, 3300], [39, 0.21, 3500]], columns=['年龄(岁)', '负债比率', '月收入(元)'])
from sklearn.preprocessing import StandardScaler
X_new = StandardScaler().fit_transform(X)
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X_new)
X_transformed = pca.transform(X_new) 使用pca.components_获取线性组合中的系数:应为PCA(n_components=2)打印出来的pca.components_有两行:
array([[ 0.52952108, 0.61328179, 0.58608264],
[-0.82760701, 0.22182579, 0.51561609]])2、案例 - 人脸识别模型
(1)背景
人脸识别是基于人的脸部特征信息进行身份识别的一种生物识别技术。该技术蓬勃发展,应用广泛,例如:人脸识别门禁系统,刷脸支付软件,公安人脸识别系统。这一节我们便以一个人脸识别模型来讲解如何在实战中应用PCA主成分分析算法。该节所讲的人脸识别的本质其实是根据每张人脸不同像素点的颜色不同来进行数据建模与判断,人脸的每个像素点的颜色都有不同的值,这些值可以组成人脸的特征向量们,不过因为人脸上的像素点过多,所以特征变量过多,因此需要利用PCA进行主成分分析进行数据降维。
(2)人脸数据读取、处理与变量提取
1、读取人脸照片数据
首先从照片数据集中导入所需要识别的人脸照片,该数据集含有40个人的照片,每人10张,共400张。这里使用的数据集是纽约大学公开的Olivetti Faces人脸数据库,其网址为:https://cs.nyu.edu/~roweis/data/olivettifaces.gif,原图是一张图,笔者将其拆分成400张jpg格式的图方便之后使用。
在Python中打开这些图片然后进行识别:
import os
names = os.listdir('olivettifaces')第2行代码使用os库的listdir()方法返回指定的文件夹中包含的文件或文件夹的名字的列表,这里的olivettifaces文件夹就是存储400张人脸照片的文件夹,这里使用的是文件相对路径。通过names[0:5]展示前五项结果:
第一部分是该张照片对应的人脸编号
第二部分是固定分隔符"_"
第三部分是该张照片在该人脸10张照片中的顺序编号
第四部分是文件的后缀".jpg"
通过如下代码在Python中查看这些图片:
from PIL import Image
img0 = Image.open('olivettifaces\\' + names[0])
img0.show()2、人脸数据处理 - 特征变量提取
已经可以读取人脸图片后,我们需要将人脸图片转换成机器学习比较好处理的数值类型数据,这些数字就是我们之后用来训练模型的特征变量X。这里处理人脸的方式和第七章处理手写数字图片的方式非常类似,都是根据人脸各个地方颜色的不同,获取其地方颜色的数值(颜色是有数值的,不同颜色的值不同),从而将图片转换为数字
import numpy as np
img0 = img0.convert('L')
img0 = img0.resize((32, 32))
arr = np.array(img0)此时如果觉得如果觉得numpy格式的arr不好观察,则可以通过pandas库将其转为DataFrame格式进行观察,代码如下:
import pandas as pd
pd.DataFrame(arr)
arr = arr.reshape(1, -1)
print(arr.flatten().tolist())演示完第一张人脸图片是如何将图片数据转换为数值数据后,我们就可以通过for循环将所有人脸图片都转换成数值数据,从而构造相应的特征变量了,代码如下:
X = [] # 特征变量
for i in names:
img = Image.open('olivettifaces\\' + i)
img = img.convert('L')
img = img.resize((32, 32))
arr = np.array(img)
X.append(arr.reshape(1, -1).flatten().tolist())二维表格如下图所示:
3、人脸数据处理 - 目标变量提取
其中names[0]为第一张图片的文件名:10_0.jpg,split()函数根据“_”符号将文件名分割为两部分,通过[0]提取第一部分,也即人的编号:10。因为split()函数分割完是以字符串形式保存,但是目标变量y是数字形式的,所以需要通过int()函数将字符串转为数字,代码如下:
print(int(names[0].split('_')[0]))通过for循环提取400张人脸图片的目标变量了,代码如下:
y = []
for i in names:
img = Image.open('olivettifaces\\' + i)
y.append(int(i.split('_')[0]))
print(y) (3)数据划分与降维
1、划分训练集和测试集
train_test_split()函数训练集和测试集数据,代码如下:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)2、PCA数据降维
X共有1024列,也即有1024个特征变量,这么多特征变量可能带来过拟合以及提高模型的复杂度等的问题,因此我们需要对特征变量进行PCA主成分分析降维:
from sklearn.decomposition import PCA
pca = PCA(n_components=100)
pca.fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)(4) 模型的搭建与使用
1、模型搭建
使用K近邻算法分类器进行模型搭建,代码如下:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(X_train_pca, y_train) 2、模型预测
测值和实际值进行对比:
y_pred = knn.predict(X_test_pca)
print(y_pred)
import pandas as pd
a = pd.DataFrame()
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)通过如下代码可以查看测试集的预测准确度:
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)3、模型对比(数据降维与不降维)
这里还可以比较下数据降维与不降维时的效果对比,不使用数据降维的代码如下所示:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)