本章讲述数据结构中的六大排序算法 欢迎大佬们踊跃讨论，感谢大家支持！ 我的博客主页链接

一.插入排序

1.1 直接插入排序

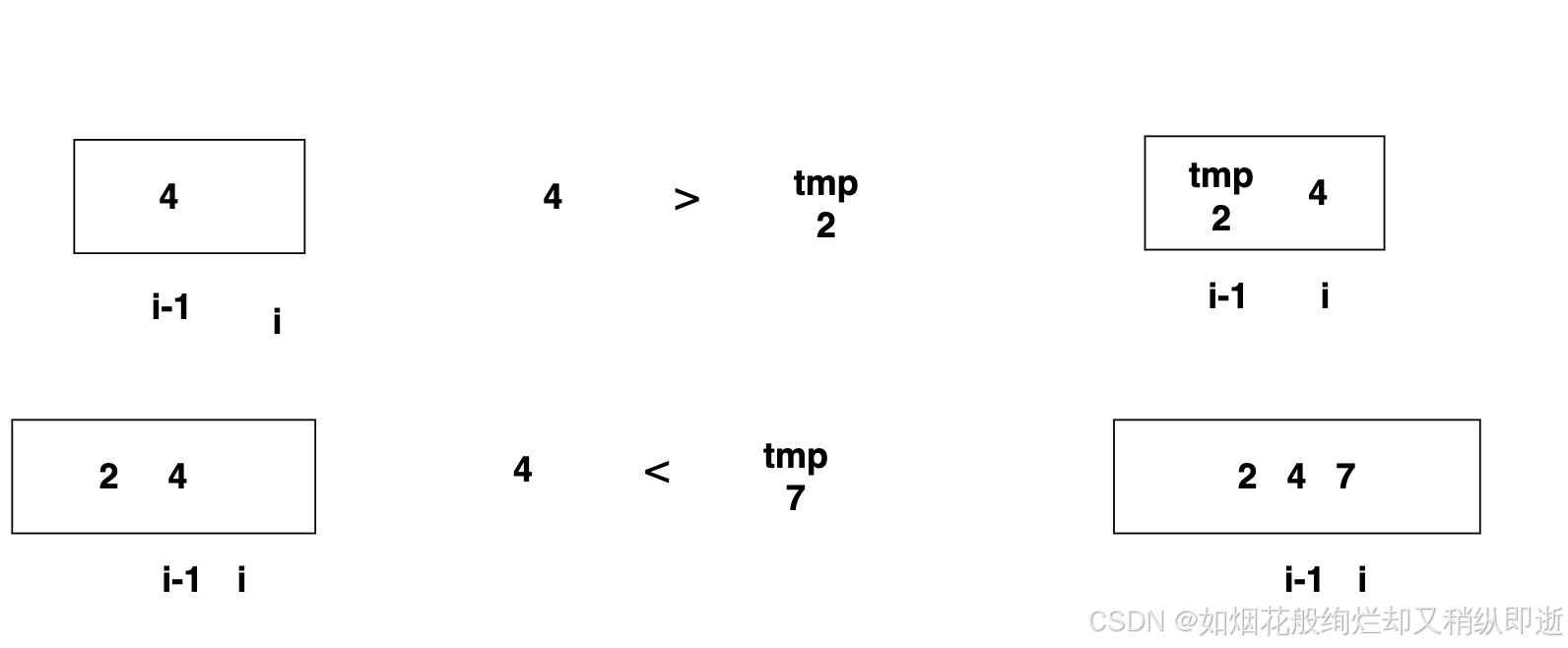
1.已知第一个元素如果不包含其他元素，没有元素可以比较，为有序。
2.我们可以直接从第二个元素i开始，创建一个对象tmp来接下标元素，如果比前一个元素小，前一个元素往后移动，tmp插入i-1下标
3.当元素大于或者等于时，则tmp直接放在i位置即可。

  public static void insertSort(int[] array){
        for(int i=1;i<array.length;i++){//由数组1下标开始进行比较
            int tmp=array[i];
            int j=i-1;
            for(;j>=0;j--){
                if(tmp<array[j]){
                    array[j+1]=array[j];//将j放入j+1位置
                }else{
                //进入else则为有序，break跳出嵌套循环
                    break;
                }
            }
      //当嵌套的for循环一直在比较最小值tmp，知道为-1跳出循环，这里需要j+1
      //当大于时候，因为i-1赋值给j，break跳出后j需要+1下标值得到tmp
            array[j+1]=tmp;
        }
    }

时间复杂度:最坏情况时间复杂度为O(N*N)
最好情况时间复杂度为O(N)
空间复杂度O(1)
稳定排序

1.2 希尔排序

希尔排序又称缩小增量法。
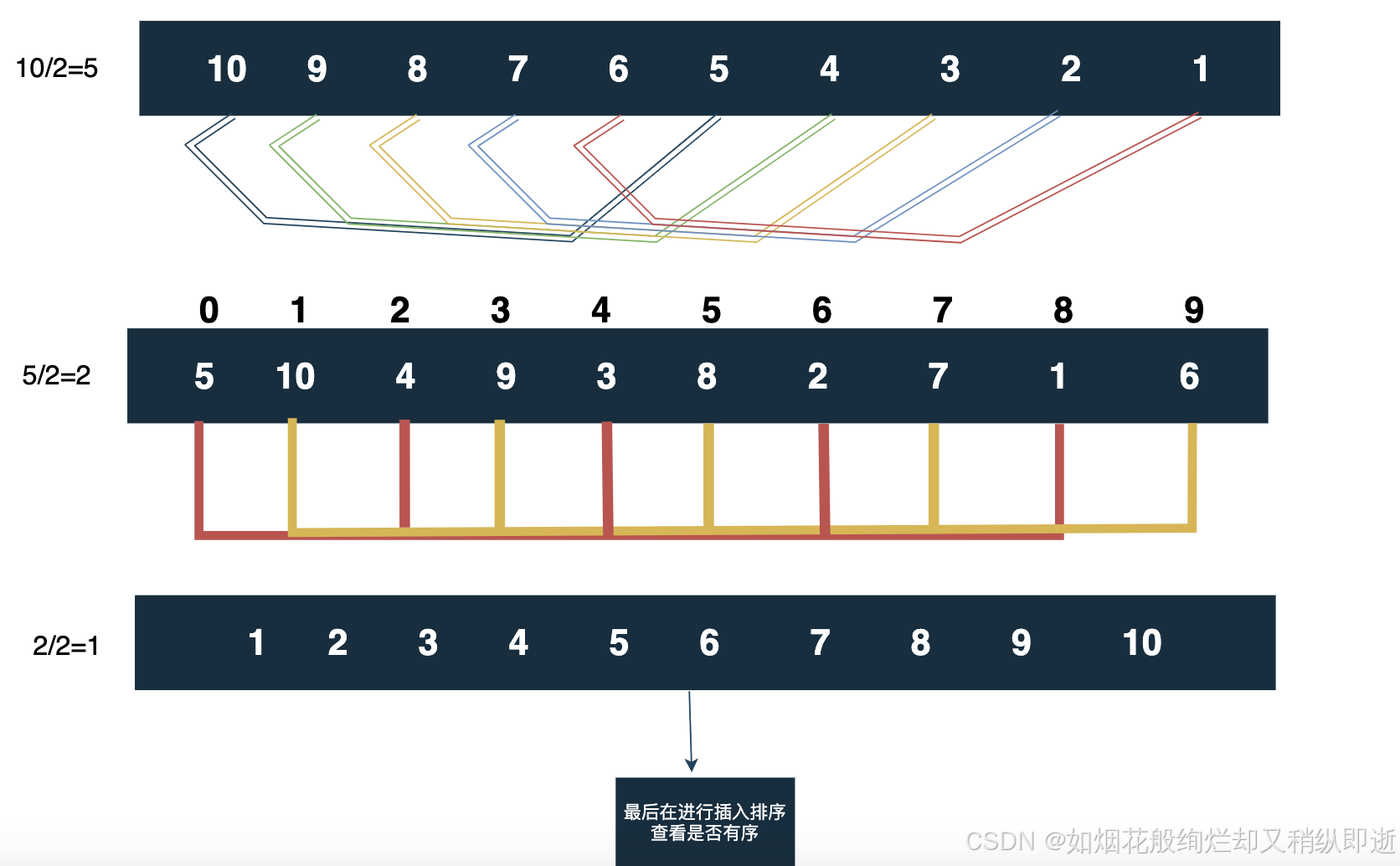
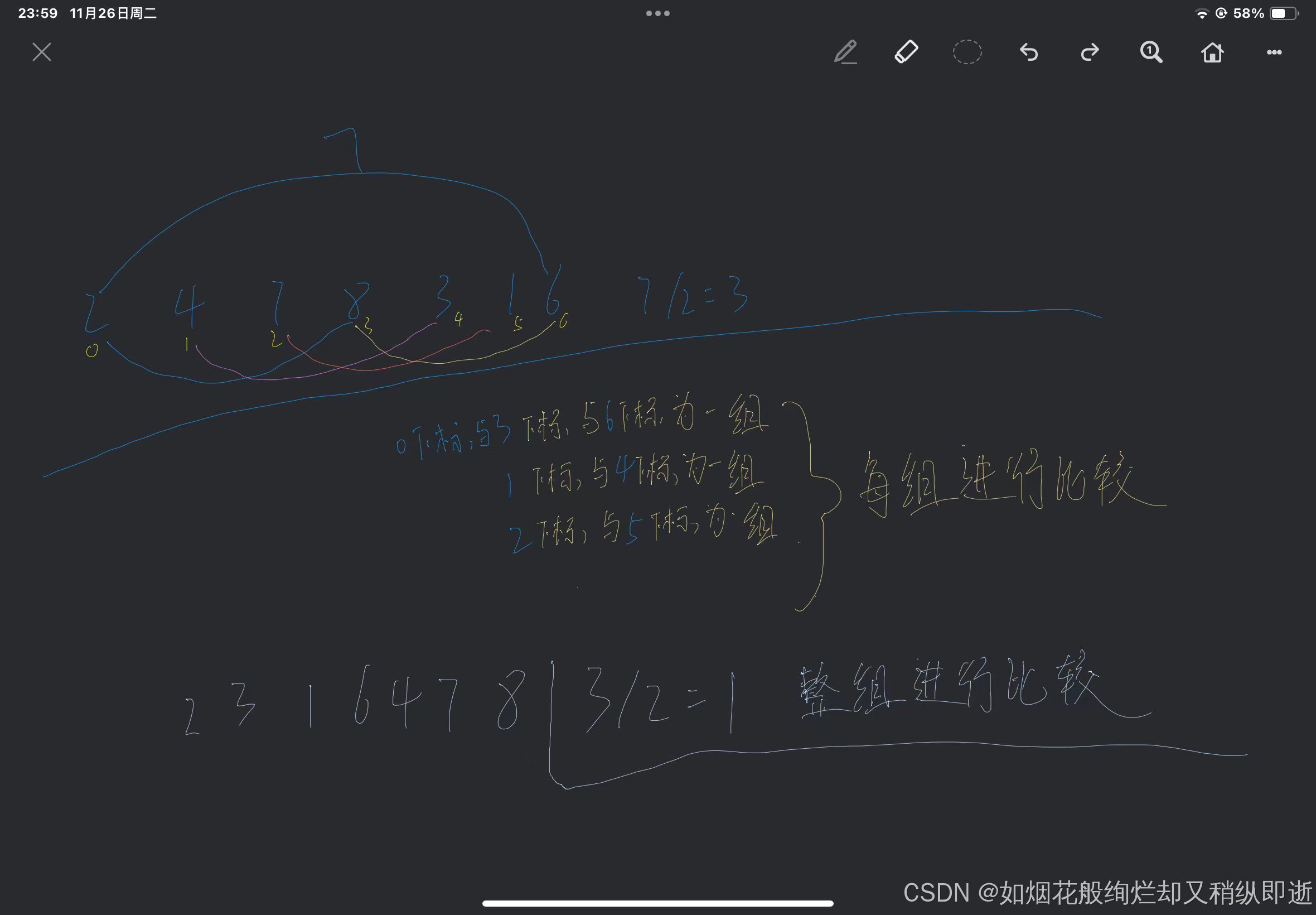
希尔排序的思想，定义一个整数，将待排序数组元素长度分成多个组，每一个组进行插入排序，重复上述分组，此时为预排序。当到达1时，将所有记录好的元素在一组中进行排序。
每一次分组排序后都变为有序，每组数据由少变多，越来越有序。

划分为n/2组进行比较，根据n/2的距离来划分每一组的数量。

   public static void shellSort(int[] array){
        int gap=array.length;
        while(gap>1){
            gap/=2;//将数组/2，有多组变少组直到为1
            shell(array,gap);
        }
    }
    public static void shell(int[] arr,int gap){
    //从gap开始遍历
        for(int i=gap;i<arr.length;i++){
        //获取gap下标的值
            int tmp=arr[i];
            求i-gap个差距得到j值
            int j=i-gap;
            for(;j>=0;j-=gap){
                if(tmp<arr[j]){
                    arr[j+gap]=arr[j];
                }else{
                    break;
                }
            }
            arr[j+gap]=tmp;
        }
    }

时间复杂度O(N^1.25)
空间复杂度O(1)

二.选择排序

2.1 单向选择排序

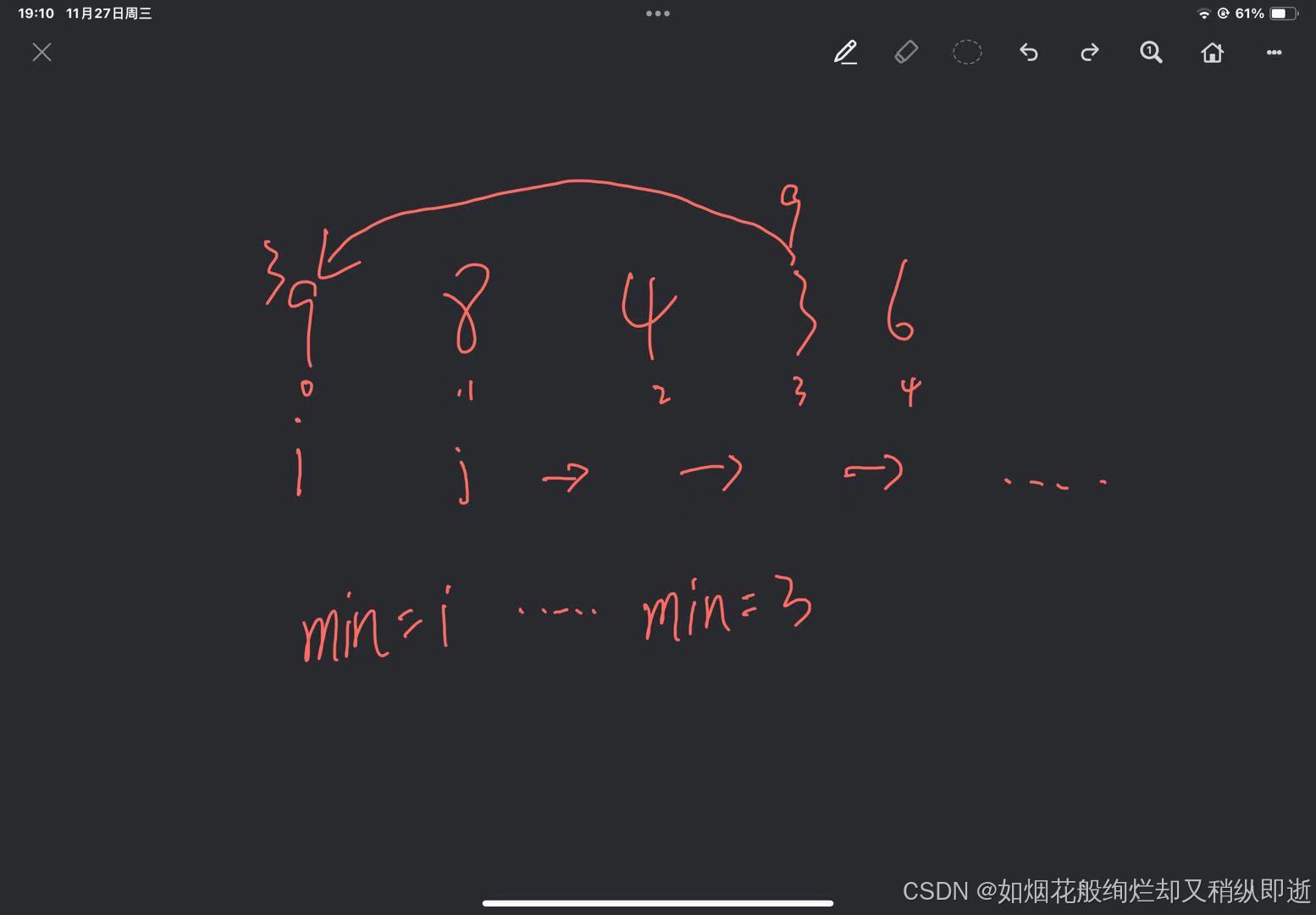
单向选择排序通过定义minIndex值来获取最小的元素下标，然后与0下标进行交换

   public static void selectSort2(int[] array){
        for(int i=0;i<array.length;i++){
            int minIndex=i;

            for(int j=i+1;j<array.length;j++){
                if(array[j]<array[minIndex]){
                    minIndex=j;
                }
            }
            swap(array,minIndex,i);
        }
    }

2.2双向选择排序

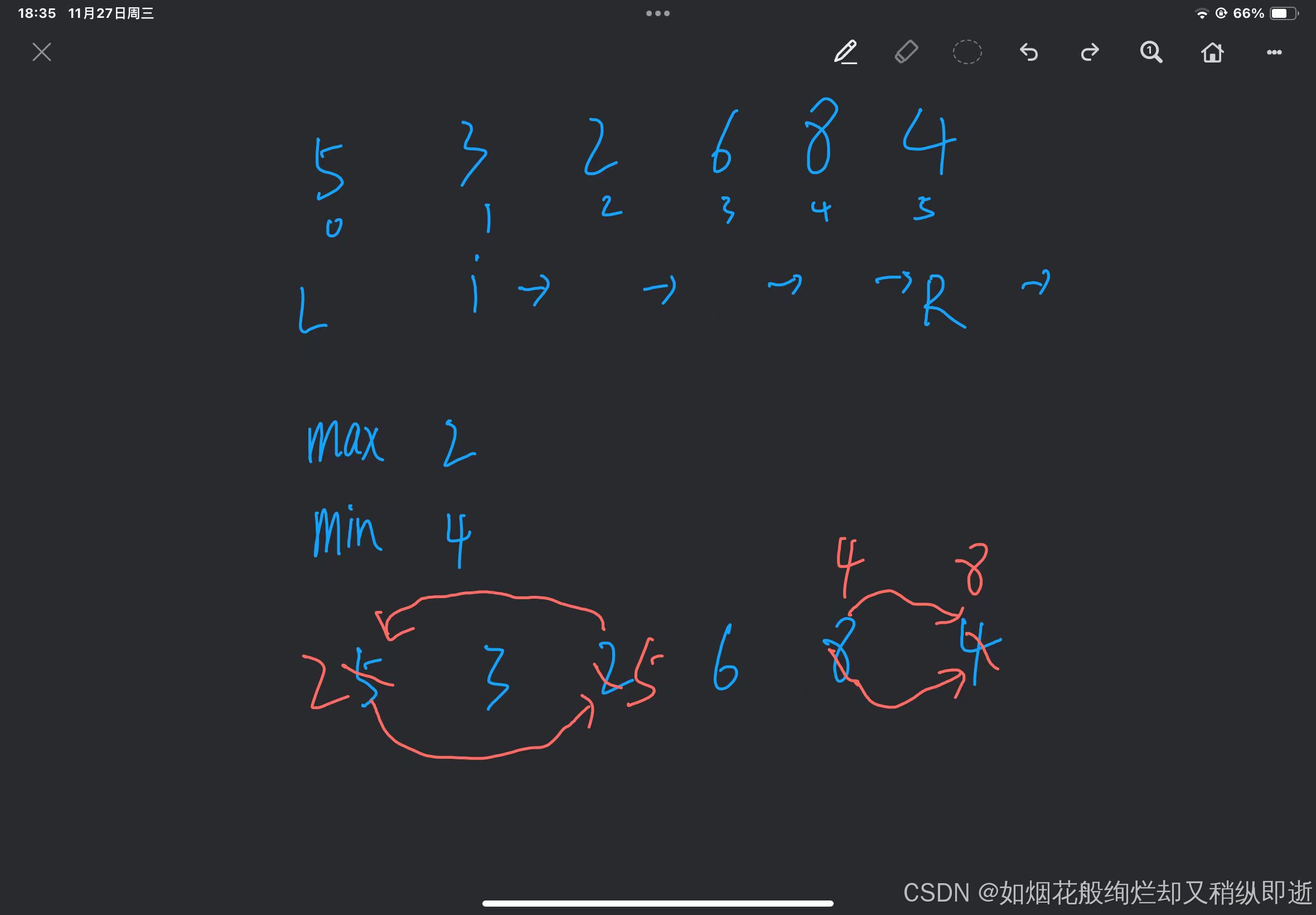
双向选择排序是我们通过定义起始位置和终点位置的下标作为条件，通过初始位置筛选最大值和最小值的下标，将最大值下标与尾部交换，最小值下标与初始位置交换，然后继续重复上述，知道筛选完成。

这里如果max的最大值为0下标的时候，max已经被 minIndex交换，maxIndex等于minIndex获取最大元素的下标值即可。

 public static void selectSort(int[] array){
        //起始位置和末尾的下标值
        int left=0;
        int right=array.length-1;
        while(left<right){
            //都从0下标开始比较
            int maxIndex=left;
            int minIndex=left;
            for(int i=left+1;i<=right;i++){
                if(array[i]<array[minIndex]) minIndex=i;
                if(array[i]>array[maxIndex]) maxIndex=i;
            }
            swap(array,left,minIndex);
            //如果0下标就是maxIndex的最大值，minIndex的位置就是maxIndex的最大值
            if(maxIndex==left)maxIndex=minIndex;
            swap(array,right,maxIndex);
            left++;
            right--;
        }
    }
    

时间复杂度：O(N^2)
空间复杂度：O(1)

2.3 堆排序

堆序详情堆排序

 //创建二叉堆
    public static void createHeap(int[] array){
        for(int parent=(array.length-1-1)/2;parent>=0;parent--){
            siftDown(array,parent,array.length);
        }
    }
    private static void siftDown(int[] array,int parent,int size) {
        int child=2*parent+1;
        while(child<size){
            if(child+1<size&&array[child]<array[child+1]){
                //child是左右孩子的最大值
                child=child+1;
            }
            if(array[child]>array[parent]){
                //交换孩子与父亲
                swap(array,child,parent);
                //调整父亲节点和孩子节点
                parent=child;
                child=(2*parent)+1;
            }else{
                break;
            }
        }
    }
    //根据创建好的大跟堆，通过最后一个下标与0下标交换后缩小堆的范围，直到称为有序数组
    public static void heapSort(int[] array){
        createHeap(array);
        int end=array.length-1;
        while(end>0){
            swap(array,0,end);
            siftDown(array,0,end);
            end--;
        }
    }

时间复杂度O(N*logN)
空间复杂度O(1)

三.交换排序

3.1 冒泡排序

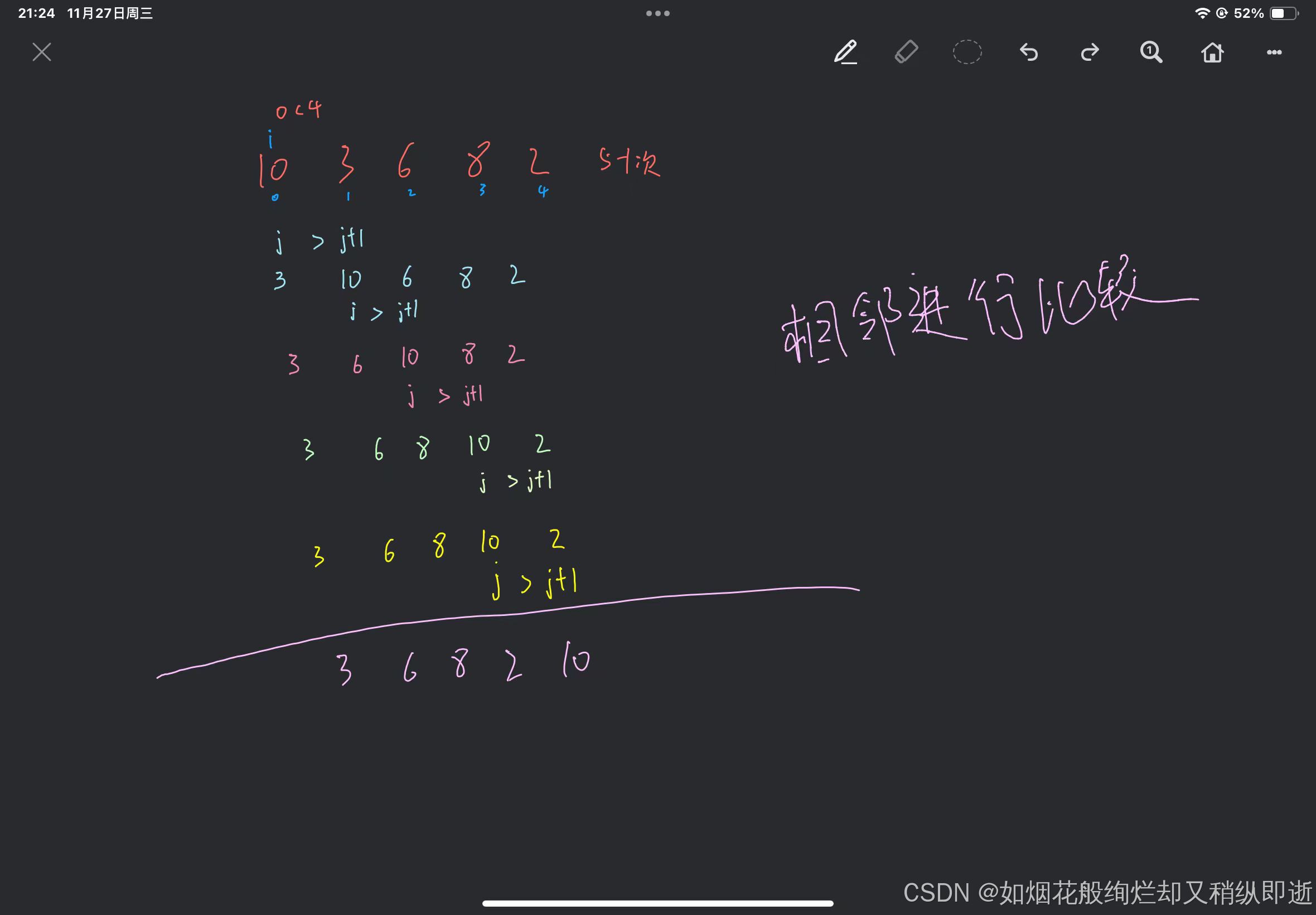
冒泡排序是一种较为简单的排序算法，它循环需要排序的元素，依次比较相邻的两个元素，如果顺序错误就进行交换，直至没有元素交换，完成排序，若对数组n个元素进行比较，则需要比较n-1次，最后一个元素已经被前n-1个元素排序好。
排序一次将len-1最大值放到最后，直到有序
本代码中的flag来记录是否有序，如果有序，则直接跳出循环。

 public static void bubbleSort(int[] array){
        for(int i=0;i<array.length-1;i++){
            boolean flag=false;//这里标记一下，每一趟中，给flag置为false，当每趟为有序后，则不进入if语句直接停止循环
            for(int j=0;j<array.length-1-i;j++){
                if(array[j]>array[j+1]){
                    swap(array,j,j+1);
                    flag=true;
                }
            }
            if(!flag){
                break;
            }
        }
    }

时间复杂度：最好情况下：O(n)
最坏情况下：O(n^2)
空间复杂度:O(1)
稳定排序

3.2 快速排序

3.2.1 Hoare排序

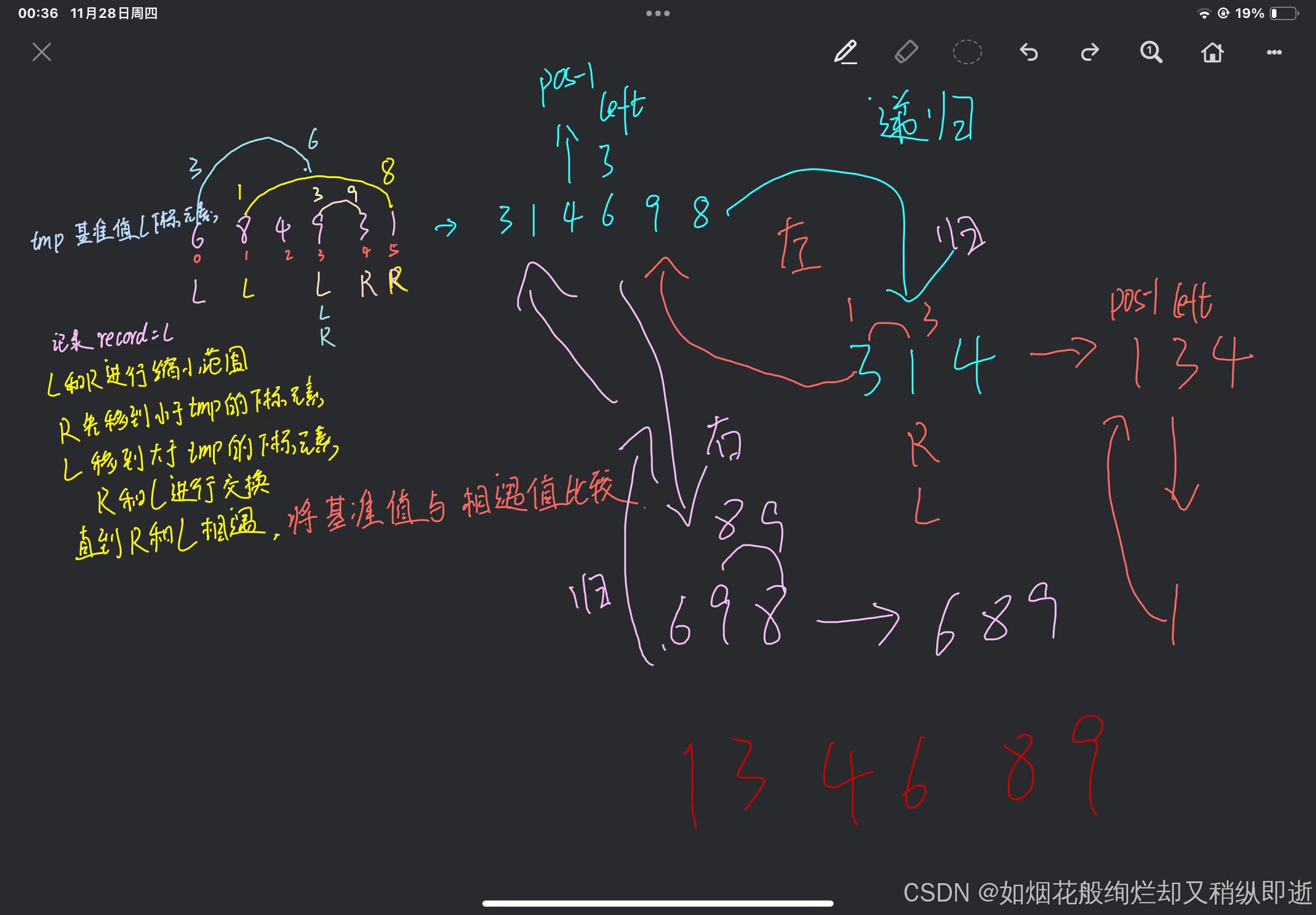
1.首先设定一个分界值，通过该分界值将数组分成左右两部分。
2、将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于分界值，而右边部分中各元素都大于或等于分界值。
3、然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

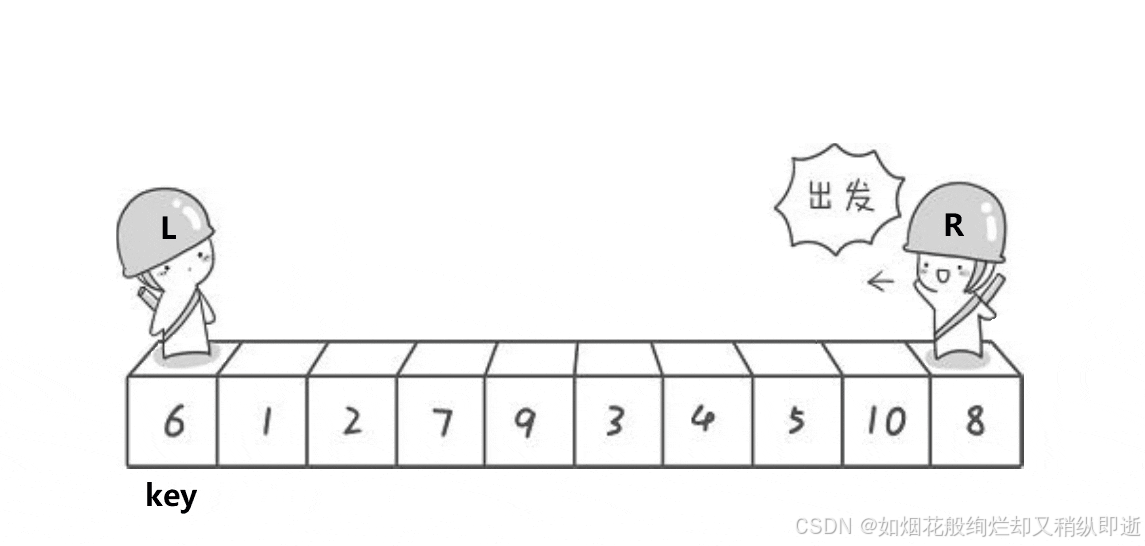
这里定义一个left为左，right为右，将任意左右位置两边定义一个基准值，根据基准值的大小，直到left为大于基准值数，right为小于基准值数停下，若定义左边为基准值则右边先走，同理右边为基准值左边先走。

 //快速排序
    public static void quickSort(int[] array){
        //记录左起始位置和右边的结束位置进行递归
        quick(array,0,array.length-1);
    }
public static void inSert(int[] array,int left,int right){
        for(int i=left+1;i<=right;i++){
            int tmp=array[i];
            int j=i-1;
            for(;j>=left;j--){
                if(array[j]>tmp){
                    array[j+1]=array[j];
                }else {
                    break;
                }
            }
            array[j+1]=tmp;
        }
    }
    private static void quick(int[] array, int left, int right) {
        if(left>=right)return ;//说明两个相遇或者走出范围
        //当长度少时直接插入排序
        if(right-left+1<=10){
            inSert(array,left,right);
            return ;
        }
        int index = middleNum(array,left,right);
        System.out.println("index下标值:"+index);
        //用来交换left和right范围内元素且最终将首位元素与相遇值交换
        swap(array,left,index);
        int pos=partitionPointer(array,left,right);//递归
        quick(array,left,pos-1);
        quick(array,pos+1,right);
    }

    private static int partitionHoare(int[] array, int left, int right) {
        int record=left;//记录left最后交换
        int tmp=array[left];//比较大小
        while(left<right){
            while(left<right&&array[right]>=tmp){//右边找到小于tmp
                right--;
            }
            while(left<right&&array[left]<=tmp){//左边找到大于tmp
                left++;
            }
            swap(array,left,right);
        }
        //这里left与right相遇
        swap(array,record,left);
        return left;
    }

时间复杂度：最坏情况下N*(logN)
最好情况下：O(N^2) 有序或者逆序情况下
空间复杂度:最好情况下O(logN)
最坏情况下：O(N) 有序或者逆序情况下
数据多时因递归可能容易栈溢出

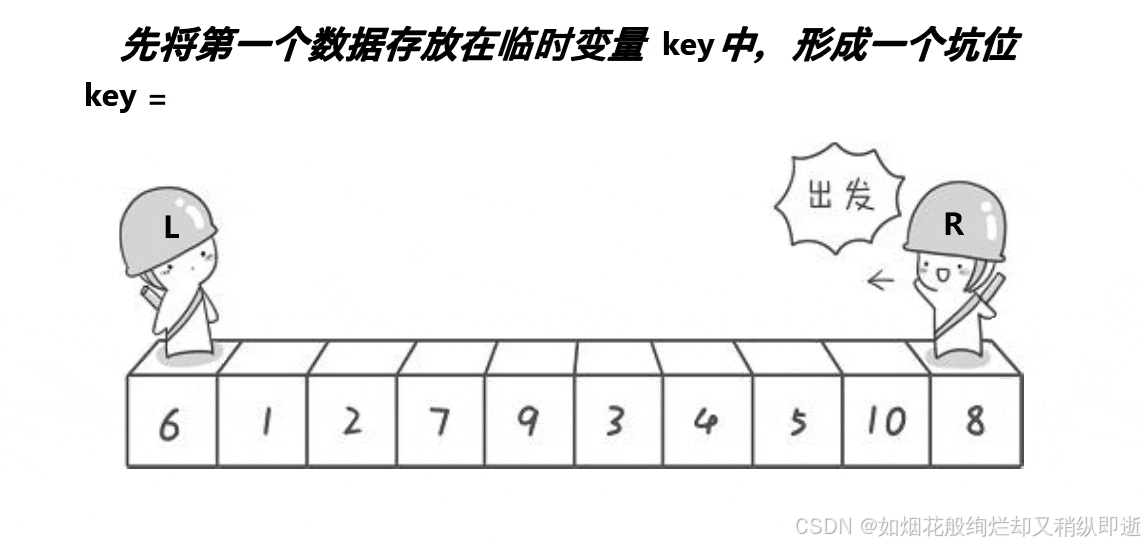
3.2.2 挖坑法

1.由左或者右选出第一个坑位记录元素值，放入key中，创建left和right对数组遍历，当选左坑右走，右坑左走，直到right和left相遇后将记录的坑位元素值放入即可。

 public static void quickSort(int[] array){
        //记录左起始位置和右边的结束位置进行递归
        quick(array,0,array.length-1);
    }
    
public static void inSert(int[] array,int left,int right){
        for(int i=left+1;i<=right;i++){
            int tmp=array[i];
            int j=i-1;
            for(;j>=left;j--){
                if(array[j]>tmp){
                    array[j+1]=array[j];
                }else {
                    break;
                }
            }
            array[j+1]=tmp;
        }
    }
    private static void quick(int[] array, int left, int right) {
        if(left>=right)return ;//说明两个相遇或者走出范围
        if(right-left+1<=10){
            inSert(array,left,right);
            return ;
        }
        int index = middleNum(array,left,right);
        System.out.println("index下标值:"+index);
        //用来交换left和right范围内元素且最终将首位元素与相遇值交换
        swap(array,left,index);
        int pos=partitionPointer(array,left,right);//递归
        quick(array,left,pos-1);
        quick(array,pos+1,right);
    }
    
    private static int partitionPit(int[] array, int left, int right) {
        int record=array[left];//记录起始坑位
        while(left<right){
            while(left<right&&array[right]>=record){//右边找到小于tmp
                right--;
            }
            //说明找到小于tmp的值
            array[left]=array[right];
            while(left<right&&array[left]<=record){//左边找到大于tmp
                left++;
            }
            //说明找到大于tmp的值
            array[right]=array[left];
        }
        //这里left与right相遇后将记录的首个坑填入
        array[left]=record;
        return left;
    }

3.2.3 前后指针法

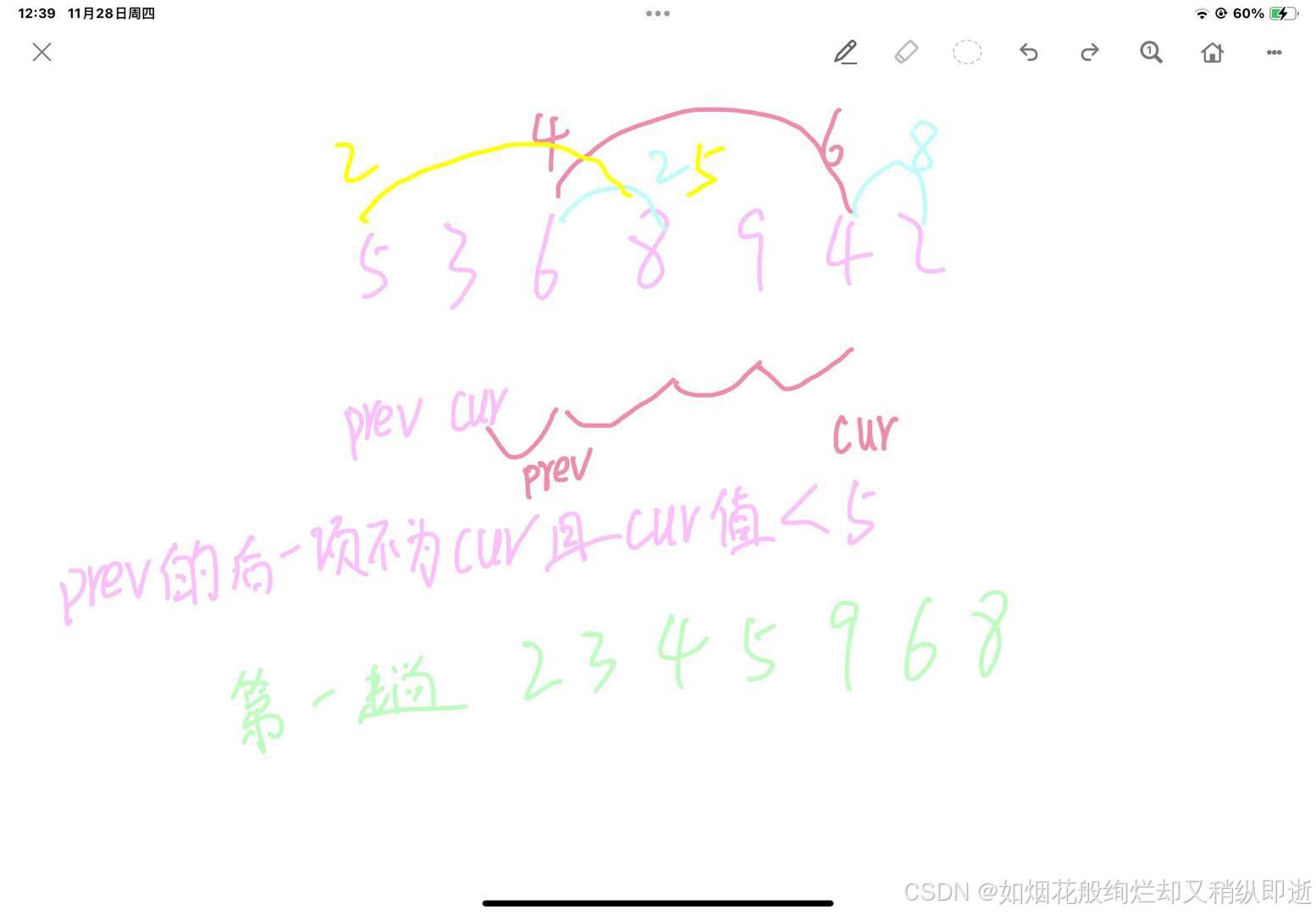
cur指向起始位置+1，pre是cur的前一位
判断条件：如果cur找到基准值（最初位置key为5），前一项的条件满足后prev向后走不为cur（为cur则不交换），直到prev在前cur在后且cur<基准值
cur如果大于基准值，直到cur找到小于基准值的数或者走完，直到递归调整为升序。

   public static void quickSort(int[] array){
        //记录左起始位置和右边的结束位置进行递归
        quick(array,0,array.length-1);
    }


public static void inSert(int[] array,int left,int right){
        for(int i=left+1;i<=right;i++){
            int tmp=array[i];
            int j=i-1;
            for(;j>=left;j--){
                if(array[j]>tmp){
                    array[j+1]=array[j];
                }else {
                    break;
                }
            }
            array[j+1]=tmp;
        }
    }
    private static void quick(int[] array, int left, int right) {
        if(left>=right)return ;//说明两个相遇或者走出范围
        if(right-left+1<=10){
            inSert(array,left,right);
            return ;
        }
        int index = middleNum(array,left,right);
        System.out.println("index下标值:"+index);
        //用来交换left和right范围内元素且最终将首位元素与相遇值交换
        swap(array,left,index);
        int pos=partitionPointer(array,left,right);//递归
        quick(array,left,pos-1);
        quick(array,pos+1,right);
    }

    private static int partitionPointer(int[] array, int left, int right) {
        //记录cur的前一项
     int Prev=left;
     int cur=left+1;
     while(cur<=right){
         //cur与起始位置比较只有小于才能进行交换且prev不为cur
         if(array[cur]<array[left]&&array[++Prev]!=array[cur]){
             swap(array,cur,Prev);
         }
         cur++;
     }
     //交换最后记录的cur的值
     swap(array,left,Prev);
     return Prev;
    }

3.4 非递归快速排序

这里非递归排序的情况下，因为每次最左边的数我们需要申请一个栈来记录其区间值，出栈由区间值一步步缩小取值的范围并进行交换，重复上述即可。

 public static void quickNor(int[] array){
      quickSortNor(array,0,array.length-1);
    }

    private static void quickSortNor(int[] array, int left, int right) {
        Stack<Integer> stack=new Stack<>();
        int pivot=partitionHoare(array,left,right);
        if(pivot>left+1){
            stack.push(left);
            stack.push(pivot-1);
        }
        if(pivot+1<right){
            stack.push(pivot+1);
            stack.push(right);
        }
        while(!stack.isEmpty()){
            right = stack.pop();
            left = stack.pop();
            pivot=partitionHoare(array,left,right);
            if(pivot>left+1){
                stack.push(left);
                stack.push(pivot-1);
            }
            if(pivot+1<right){
                stack.push(pivot+1);
                stack.push(right);
            }
        }

四.归并排序

4.1 递归归并排序

定义一个分界线mid来获取其中间值，递归左边和右边，每次进入方法进行排序
将左起始到中间值与中间值到右侧比较，创建一个数组来记录，排序后放到数组中，最后让原数组接收。

    public static void mergeSort(int[] array){
        mergeSortM(array,0,array.length-1);
    }

    private static void mergeSortM(int[] array, int left, int right) {
    //知道left和right相遇返回
        if(left>=right)return ;
        int mid=(left+right)/2;
      //以中间值作为分区，递归左边和右边
        mergeSortM(array,left,mid);
        mergeSortM(array,mid+1,right);
        //每次递归传入后进行排序
        merge(array,left,mid,right);
    }

    private static void merge(int[] array, int left, int mid, int right) {
        int[] tmpArr=new int[right-left+1];//创建一个数组接收每一次递归的数组
        int k=0;
          //记录左边的起始位置与右边起始位置
        int s1=left;
        int s2=mid+1;
        while(s1<= mid &&s2<= right){
            if(array[s1]<=array[s2]){
                tmpArr[k++]=array[s1++];
            }else{
                tmpArr[k++]=array[s2++];
            }
        }
        while(s1<= mid){
            tmpArr[k++]=array[s1++];
        }
        while(s2<= right){
            tmpArr[k++]=array[s2++];
        }
        for(int i=0;i<tmpArr.length;i++){
        //这里的left跟随着mid改变，当递归右侧时，left为mid+1
            array[i+left]=tmpArr[i];
        }
    }
}

时间复杂度：O(N*logN)
空间复杂度:O(logN)
稳定排序

4.2非递归归并排序

  private static void merge(int[] array, int left, int mid, int right) {
        int[] tmpArr=new int[right-left+1];//创建一个数组接收每一次递归的数组
        int k=0;
        //记录左边的起始位置与右边起始位置
        int s1=left;
        int s2=mid+1;
        while(s1<= mid &&s2<= right){
            if(array[s1]<=array[s2]){
                tmpArr[k++]=array[s1++];
            }else{
                tmpArr[k++]=array[s2++];
            }
        }
        while(s1<= mid){
            tmpArr[k++]=array[s1++];
        }
        while(s2<= right){
            tmpArr[k++]=array[s2++];
        }
        for(int i=0;i<tmpArr.length;i++){
            array[i+left]=tmpArr[i];
        }
    }
    
  public static void mergeNor(int[] array){
       int gap=1;//每组共有几个数据
        while(gap<array.length){
            for(int i=0;i<array.length;i=i+gap*2){
                int left=i;
                int mid=left+gap-1;
                int right=mid+gap;
                if(mid>=array.length)
                    mid=array.length-1;
                if(right>=array.length){
                    right=array.length-1;
                }
               merge(array,left,mid,right);
            }
            gap*=2;
        }
    }

五.测试运行时间代码

  // 有序
    public static void order(int[] arr){
        for(int i=0;i<arr.length;i++){
            arr[i]=i;
        }
    }
    //逆序
     public static void reverse(int[] arr){
        for(int i=0;i<arr.length;i++){
            arr[i]= arr.length-i;
        }
    }
    //无序
    public static void disorder(int[] arr){
        Random random=new Random();
        for(int i=0;i<arr.length;i++){
            arr[i]= random.nextInt(100);
        }
    }

    //测试
    public static void testSort1(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
    long startTime=System.currentTimeMillis();//开始结束记录
        Sort.shellSort(tmpArray);
    long endTime=System.currentTimeMillis();
        System.out.println("希尔排序时间："+(endTime-startTime));
    }

    public static void testSort2(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.inSert(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("插入排序时间："+(endTime-startTime));
    }

    public static void testSort3(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.selectSort2(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("双向选择排序时间："+(endTime-startTime));
    }
    public static void testSort4(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.bubbleSort(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("冒泡排序时间："+(endTime-startTime));
    }
    public static void testSort5(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.heapSort(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("堆排序时间："+(endTime-startTime));
    }
    public static void testSort6(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.quickSort(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("Hoare快速排序时间："+(endTime-startTime));
    }
    public static void testSort7(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.quickSort(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("挖坑法快速排序时间："+(endTime-startTime));
    }
    public static void testSort8(int[] arr){
        int[] tmpArray= Arrays.copyOf(arr,arr.length);
        long startTime=System.currentTimeMillis();//开始结束记录
        Sort.quickSort(tmpArray);
        long endTime=System.currentTimeMillis();
        System.out.println("前后指针法快速排序时间："+(endTime-startTime));
    }