Cut

因为数字的长度最多为10，因此可以爆搜出每一种切分位置，最后统计即可

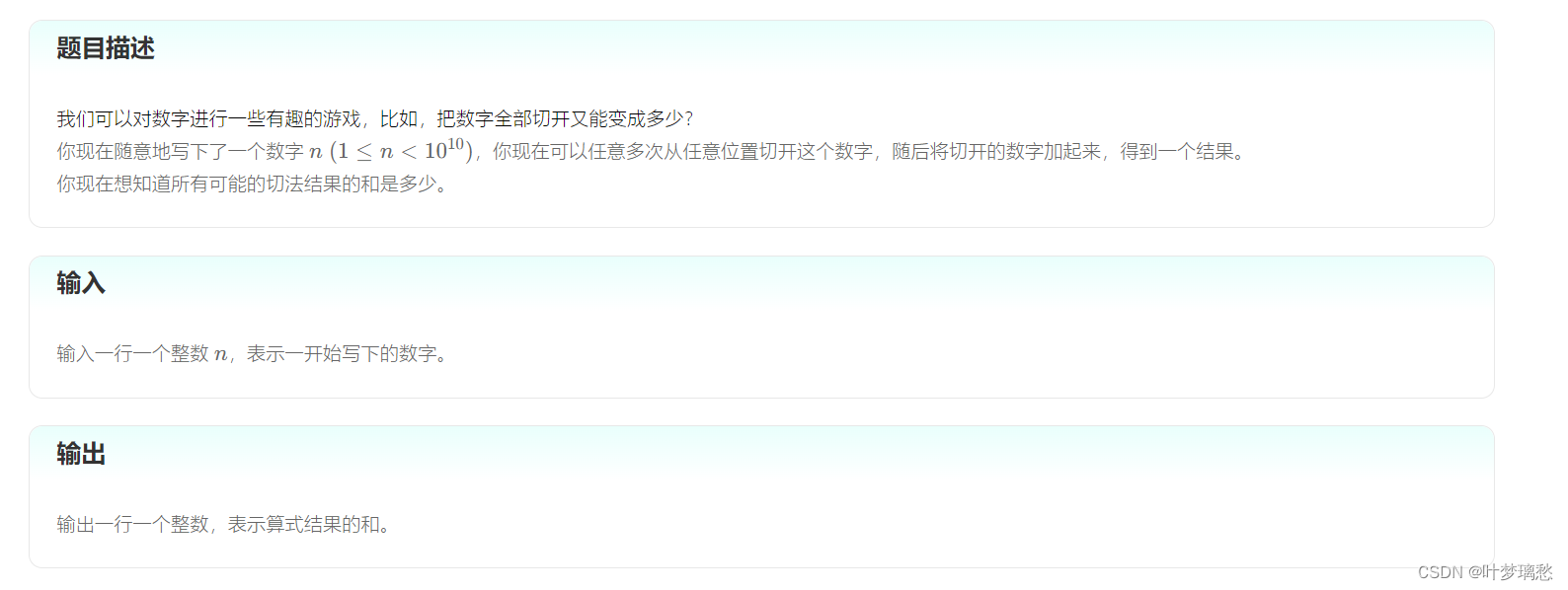
# include <bits/stdc++.h>
# define endl '\n'
# define int unsigned long long
# define pii pair<int, int> 
# define vi vector<int>
# define all(x) x.begin(),x.end()

using namespace std;

int n;
vector<int> st;

int get(string &s, int l, int r)
{
    int res = 0;
    while (l <= r) res = res * 10 + s[l ++] - '0';
    return res; 
}

void dfs(string& s, int idx, int t)
{
    if (idx == s.length()) 
    {
        st.push_back(t);
        return;
    }
    for (int i = idx; i < s.length(); i ++)
    {
        int cur = get(s, idx, i);
        dfs(s, i + 1, t + cur);
    }   
}
void solve()
{
    cin >> n;
    string s = to_string(n);
    dfs(s, 0, 0);
    cout << accumulate(all(st), 0ull);
}


signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int t = 1;
    while (t --) solve();
    return 0; 
}

Diff

数学：

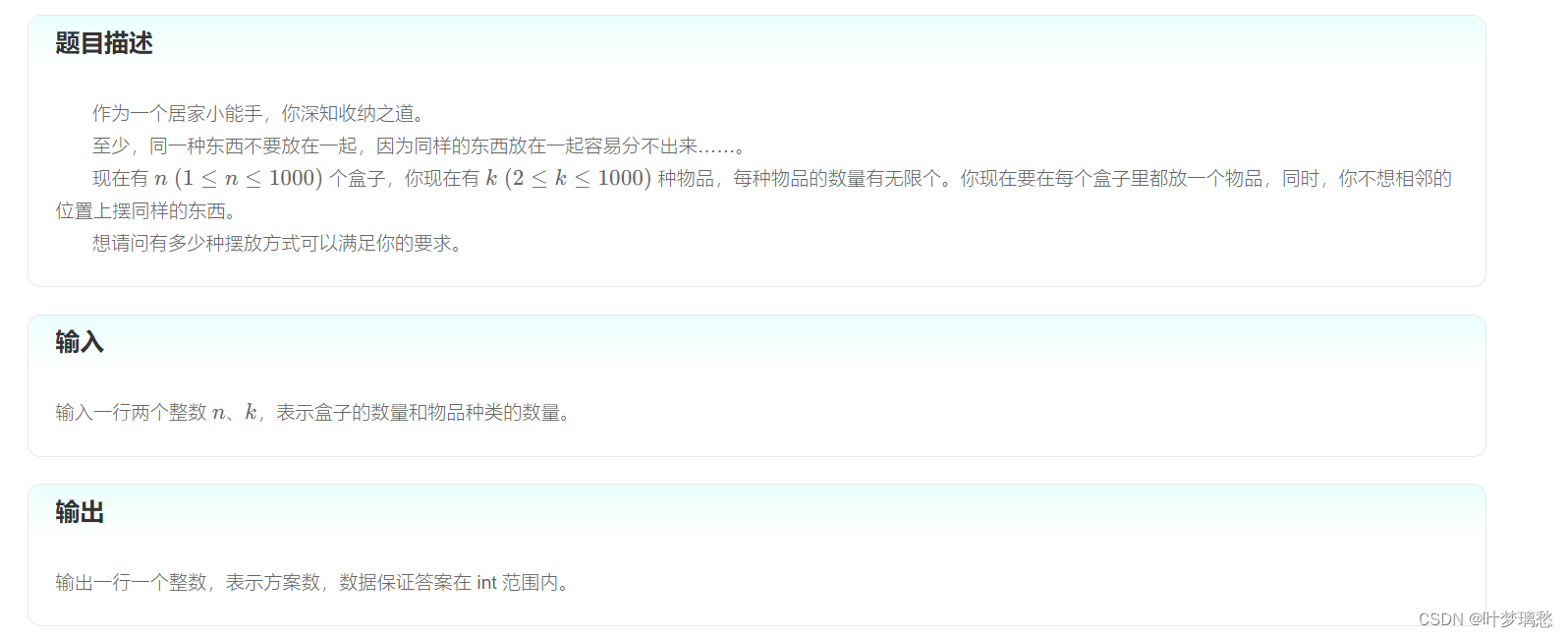
• 对于第一个位置，可以放 k 种物品
• 对于其他位置，因为不能相邻，即对于当前位置有 $k-1$ 种物品可以放
• 那么最终的方案数就是 $k\cdot (k-1{)}^{n-1}$

dp

• 状态表达：dp[i][j] 为第 i 个位置放第 k 种物品的方案数
• 状态转移：
  $$dp[i][j]=\{\begin{array}{l}1i=1\\ {\sum }_{k=1}^n(dp[i-1][k])-dp[i-1][j]\end{array}$$
• 最后把第 n 个位置的所有方案数统计即可

# include <bits/stdc++.h>
# define endl '\n'
# define int long long
# define pii pair<int, int> 
# define vi vector<int>
# define all(x) x.begin(),x.end()

using namespace std;
const int N = 1e3 + 10;
int dp[N][N];
void solve()
{
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= k; i ++) dp[1][i] = 1;
    for (int i = 1; i <= n; i ++)
    {
        for (int j = 1; j <= k; j ++)
        {
            for (int x = 1; x <= k; x ++)
            {
                if (x == j) continue;
                dp[i][j] += dp[i - 1][x];
            }
        }
    }
    int ans = 0;
    for (int i = 1; i <= k; i ++) ans += dp[n][i];
    cout << ans << endl;
}


signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int t = 1;
    while (t --) solve();
    return 0; 
}

EchoN

- 暴力$O(n^2)$肯定会超时；

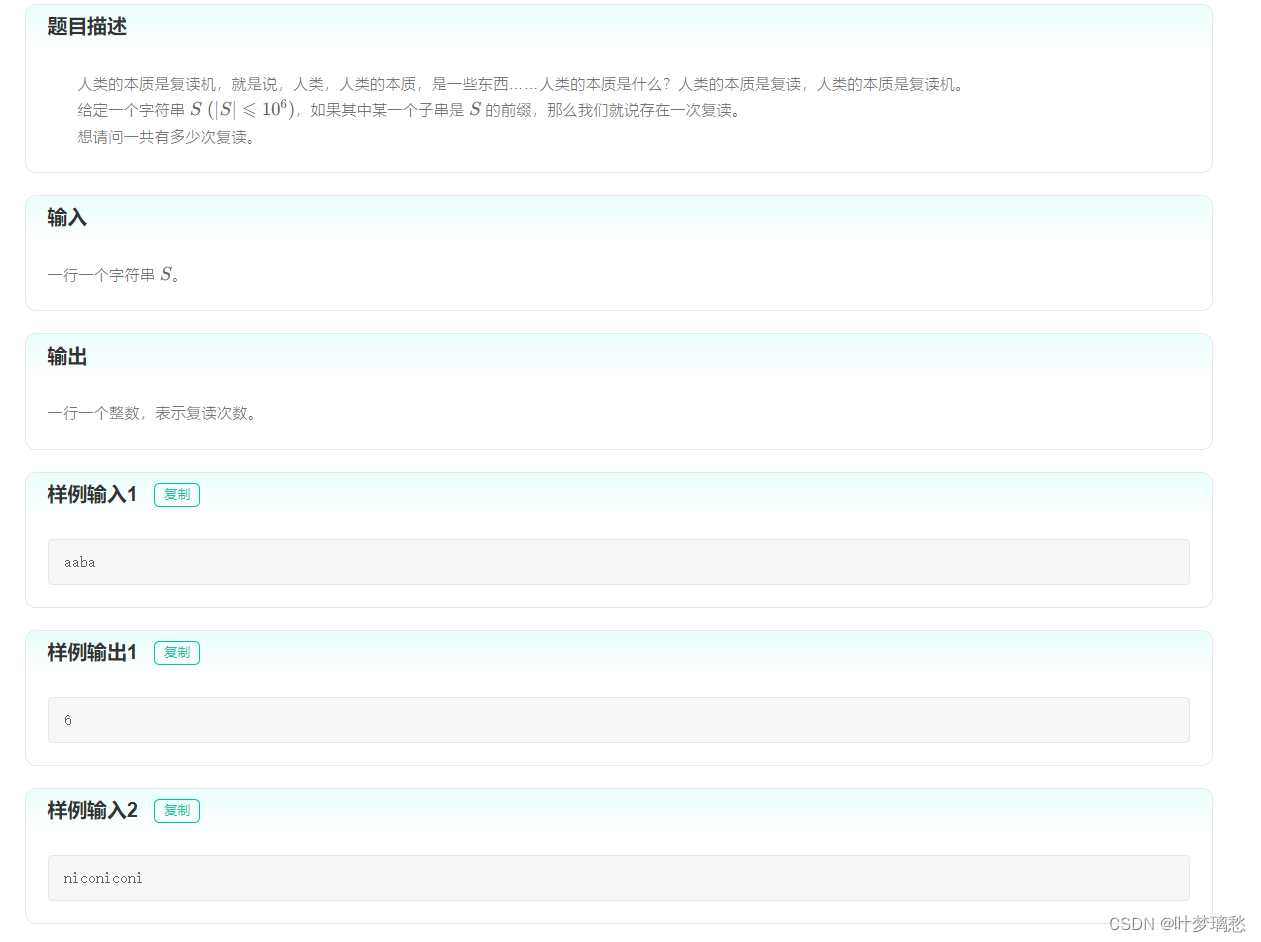
• kmp算法的 next 数组保存的是与匹配串 前缀 相同的子串在失配时所需要跳转的下一个位置

  例子： abcabcabc 的next数组为:

  index	0	1	2	3	4	5	6	7	8
  s	a	b	c	a	b	c	a	b	c
  next	-1	-1	-1	0	1	2	3	4	5

  可以看到相同前缀的子串都有一一对应，比如匹配到后面下标为 4 的字符 b 时失配了，那么就会跳转到下标1的位置

  在这个例子可以看到，最后的 abc 子串 既和 前缀 abc 相同，同时与前面 abc组成 abcabc 部分，也和前缀 abcabc 相同，

  可以发现，这个与前缀相同的子串数量和 next 跳转到 -1 的次数有关，也就是说，next数组每跳一次，答案+1

• 那么只需要处理出来 next 数组，然后就可以统计出子串与前缀相同的数目

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define pii pair<int, int>
#define vi vector<int>
#define all(x) x.begin(), x.end()
#define x first
#define y second
using namespace std;
const int N = 1e6 + 5;

void solve()
{
    string s;
    cin >> s;
    int n = s.length();
    vector<int> p(n);
    int ans = n;
    p[0] = -1;
    for (int i = 1, j = -1; i < n; i ++) 
    {
        while (j != -1 && s[i] != s[j + 1]) j = p[j];
        if (s[i] == s[j + 1]) j ++;
        p[i] = j;
        int t = p[i];
        while (t != -1) t = p[t], ans ++;
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) solve();
    return 0;
}

IMissYou!

简单模拟

# include <bits/stdc++.h>

using namespace std;

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int ans = 0, t;
    for (int i = 0; i < 7; i ++) cin >> t, ans += t;
    if (ans > 0) cout << "IMissYou!" << endl << ans << endl;
    else cout << "OvO" << endl;
    return 0; 
}

Jargonless

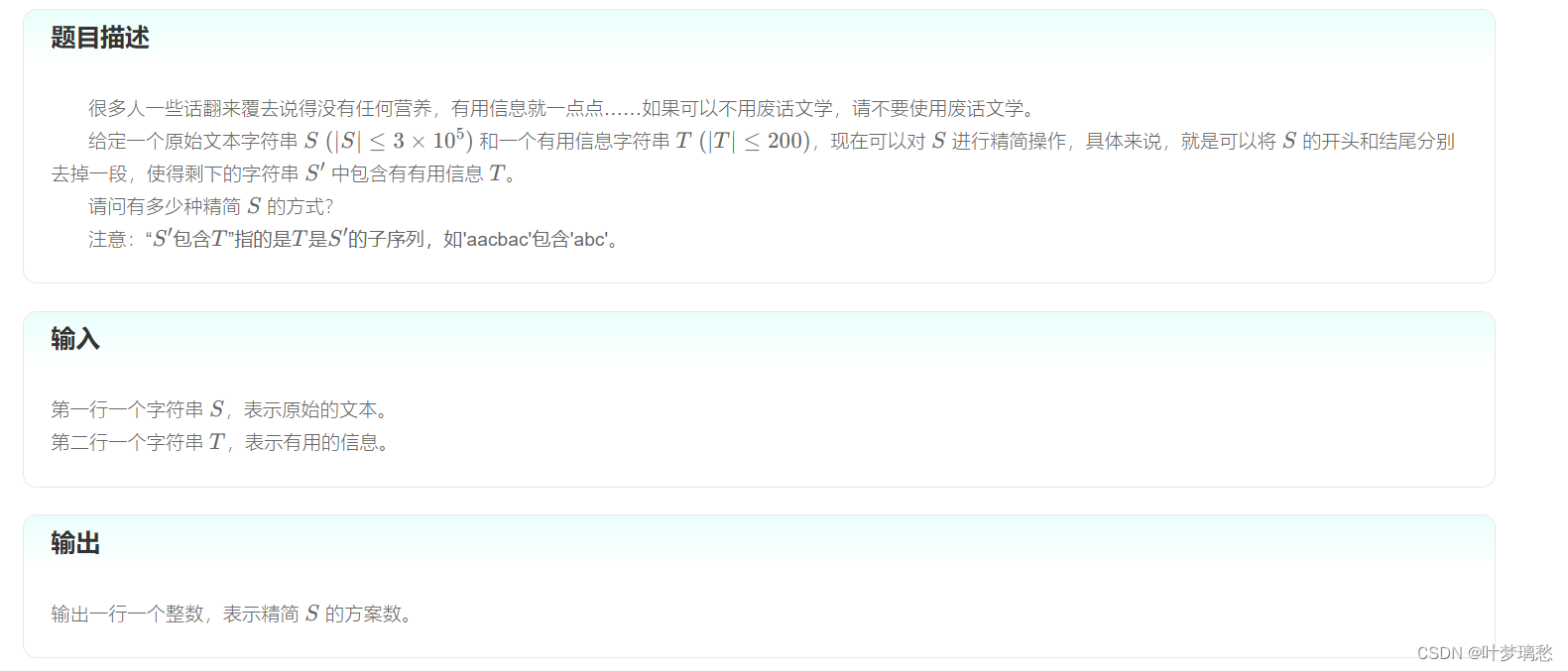
• 先找出包含T子序列的最小区间，这里可以通过记录T首个字符的位置，然后从记录的位置开始找
• 然后算每一个区间左边和右边的字符个数，用乘法原理可以得到当前区间的方案数
• 但是可以发现，可能存在某些方案重复，也就是说删除的字符重复，如果直接统计会导致答案出错，那么需要对某些地方进行优化：
  • 需要找出包含T的最长区间A，即左边界时T的第一个字符，右边界是T的最后一个字符，然后该区间左右都是上面统计时可能重复的方案，需要最后统计
  • 得到最长区间A后，对于每个包含T子序列的最小区间 B_i 都需要在这个区间进行统计，计算的方案数等于：A区间的左边界到 B_i 区间左边界字符数$ll$ $\times$ B_i 区间右边界字符数到 B_i+1 区间的右边界$rr$，保证统计的方案数不会重复
  • 最后还有区间A左右两端与区间A的方案没有统计，需要记录上

# include <bits/stdc++.h>
# define endl '\n'
# define int long long
# define pii pair<int, int> 
# define vi vector<int>
# define all(x) x.begin(),x.end()
# define x first
# define y second

using namespace std;

void solve()
{
    string s, t;
    vector<pii> st;
    int n, m;
    cin >> s >> t;
    n = s.length(), m = t.length();
    int l = 0, r = n - 1;
    while (l < r && s[l] != t[0]) l ++;
    while (r > l && s[r] != t[m - 1]) r --; //找出区间A
    int ans = 0, k = 0;
    vector<int> pos;
    for (int i = l; i <= r; i ++) 
    {
        if (s[i] == t[k]) k ++;
        if (s[i] == t[0]) pos.push_back(i); //记录需要查找的位置
    }
    if (k >= m)  //包含T子序列
    {
        for (int i = 0, j = pos[i], p = 0; i < pos.size(); j ++) //从记录的位置开始查找
        {            
            if (s[j] == t[p]) p ++; 
            if (p == m) //找到后还不一定是最小的，向左边收缩
            {
                int x = pos[i], y = j;
                while (x <= y && ~p)
                {
                    if (s[y] == t[p]) p -- ;
                    y --;
                }
                if (x != y) y ++;
                st.push_back({y, j}); //记录区间Bi
            }
            if (j == r || p == m) //查找下一个记录的位置
            {
                i ++;
                if (i >= pos.size()) break;
                j = pos[i] - 1;
                p = 0;
            } 
        }
        int size = st.size();
        for (int i = 0; i < size - 1; i ++) 
        {
            int ll = st[i].x - l, rr = st[i + 1].y - st[i].y; //统计方案数
            ans += ll * rr;
        }
        int ll = st.back().x - l, rr = r - st.back().y;
        ans += ll * rr;
        //区间A左右两端+左端与区间A内部+右端与区间A内部
        ans += (l + 1) * (n - r) + (l + 1) * (r - st.front().y) + (n - r) * (st.back().x - l);
    } 
    cout << ans << endl;
}


signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t --) solve();
    return 0; 
}

如果习惯痛苦
眼泪不会很苦
若你伤悲 让我钟声
给你安慰