省略模版代码，模板代码在最后面
div4重拳出击(bushi)，但是F题不会
更新：
·1. E题被hacked了，等一下数据
2. F题原来暴力就能解决，万万没想到，还以为会超时；更新下。

A. My First Sorting Problem

题目：
给两个整数X和Y，先输出最小值再输出最大值

思路：
模拟

static void solve() throws IOException {
    int[] a = pIntArray(0);
    int x = a[0], y = a[1];
    if (x > y) {
        out.println(y + " " + x);
    } else {
        out.println(x + " " + y);
    }
}

B. Different String

题目：
给一个仅包含小写字母的字符串S，判断重新安排顺序后的字符串能不能与S不相同，若能不相同则输出一种情况

思路：
当S仅包含一种字母时无论怎么安排都会等于S，只需要在遍历时判断是否有第二种字母出现，出现就与前面一个字母交换即可

static void solve() throws IOException {
    char[] s = in.readLine().toCharArray();
    int[] st = new int[26];
    int cnt = 0, pre = -1;
    for (int i = 0; i < s.length; i++) {
        if (st[s[i] - 'a'] == 0) {
            cnt++;
            if (pre == -1) {
                pre = i;
            }
        }

        if (cnt > 1) {
            char tmp = s[i];
            s[i] = s[pre];
            s[pre] = tmp;
            out.println("YES");
            out.println(String.valueOf(s));
            return;

        }
        st[s[i] - 'a']++;
    }
    out.println("NO");
}

C. Clock and Strings

题目：
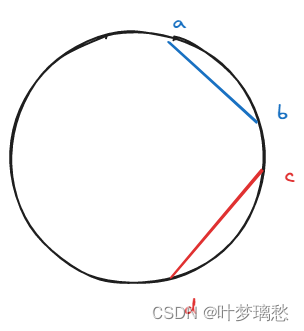
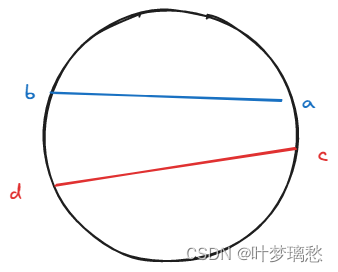
给四个互不相同且不超过12的整数a,b,c,d，在钟表上分别连接a和b、c和d，判断这两条线是否相交

思路：
假设a<b，c<d，思考什么时候不会相交：

1. 其中一条线在另一条线的旁边，此时b < c 或者 a < d
   
2. 其中一条线和另一条线类似平行，此时a < c且b>d 或者 c<a且d>b（可以理解为一条线在另一条线内部）
   
   判断出这两种情况就是没有相交，其他的就是相交

static void solve() throws IOException {
    int[] ins = pIntArray(0);
    int a = ins[0], b = ins[1], c = ins[2], d = ins[3];
    if (a > b) {
        int t = b;
        b = a;
        a = t;
    }
    if (c > d) {
        int t = c;
        c = d;
        d = t;
    }

    if ((a < c && b > d) || (c < a && d > b) || (b < c || d < a)) {
        out.println("NO");
    } else {
        out.println("YES");
    }
    }

D. Binary Cut

题目：
给一个二进制字符串S，可以进行任意切分，然后对切分后的块进行重新排列，使得排列产生的字符串是一个有序的字符串（非递减），求切分的最小块数

思路：
观察样例 110100 可以发现，如果全是 1 的块是能够放在最后面的，全是0的块可以放在最前面，但是这两部分的中间只能放下一个包含 00..01...1 形式的块；
那么对于 0 开头的子串，仅能在后面跟一次全是 1 的子串；

static void solve() throws IOException {
    char[] s = in.readLine().toCharArray();
    int ans = 0, cnt = 0;
    for (int i = 0; i < s.length; ) {
        int j = i + 1;
        if (s[i] == '0') {
            while (j < s.length && s[j] == '0') j++;
            while (cnt == 0 && j < s.length && s[j] == '1') j++;
            if (s[j - 1] == '1') {
                cnt ++;
            }
        } else {
            while (j < s.length && s[j] == '1') j++;
        }
        ans++;
        if (j - 1 > i) i = j;
        else i++;
    }
    out.println(ans);

E. Find the Car

题目：
一辆汽车在0分钟从点0出发，已知K个信号站所在位置a和到达每个信号站的时间b，在两个相邻的信号站之间汽车行驶的速度恒定，现在给q次询问，每次询问给一个整数d，求到达d的时间。

思路：
对于 d，只需要 二分 找出前一个信号站的位置和到达时间，然后就能够求出前一个信号站到下一个信号站的速度，就能够求出到达d的时间

static void solve() throws IOException {
    int[] ins = pIntArray(0);
    int n = ins[0], k = ins[1], q = ins[2];
    int[] a = pIntArray(1), b = pIntArray(1);
    double[] speeds = new double[k + 1];
    // 从1开始，方便求取0到第一个信号站的速度
    for (int i = 1; i <= k; i ++) {
        speeds[i] = (double) (a[i] - a[i - 1]) / (b[i] - b[i - 1]);
    }
    while (q -- > 0) {
        int d = pInt();
        int l = 0, r = k;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (a[mid] <= d) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        if (a[l] == d) {
            out.print(b[l] + " ");
        } else {
            out.print((long)((b[l] + (d - a[l]) / speeds[l + 1])) + " ");
        }
    }
    out.println();
}

============ hack更新 =================
上面的被下面这个数据hack掉了

1
1000000000 2 1
999999998 1000000000
999999999 1000000000
999999997

问题出在浮点数运算上，思路是没有问题的，只是最后计算的时候因为精度导致计算结果 999999997.999999998999999998 变成 999999998，然后就wa了，改了：

 static void solve() throws IOException {
     int[] ins = pIntArray(0);
     int n = ins[0], k = ins[1], q = ins[2];
     int[] a = pIntArray(1), b = pIntArray(1);
     while (q -- > 0) {
         int d = pInt();
         int l = 0, r = k;
         while (l < r) {
             int mid = l + r + 1 >> 1;
             if (a[mid] <= d) {
                 l = mid;
             } else {
                 r = mid - 1;
             }
         }
         if (a[l] == d) {
             out.print(b[l] + " ");
         } else {
             out.print(b[l] + ((long) (d - a[l]) * (b[l + 1] - b[l])) / (a[l + 1] - a[l]) + " ");
         }
     }
     out.println();
 }

F. Circle Perimeter

题目:
求圆心为(0,0)且半径分别为整数 r 和 r+1 的同心圆之间有多少个整数点，即有多少个点 (x, y) 满足 $r\le \sqrt{x^2+y^2}<r+1$

思路:
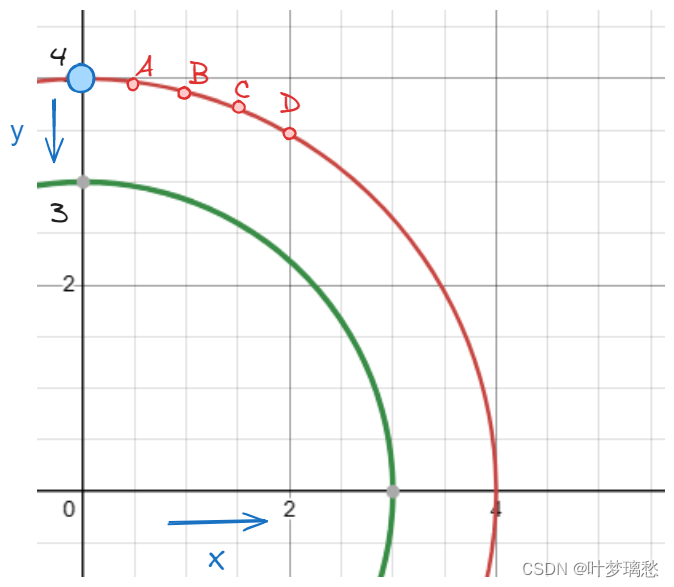
因为圆是对称的，可以只看第一象限， 假设y从r+1 开始，右边的 A、B、C、D四个点都是比(0, 4)这个点低的，同时它们到(0,0)的距离都是 r+1；也就是说，当x遍历 0到 r+1 的时候，满足条件的点的纵坐标必定小于 y ，而这个 y 随着 x 的增大不断减小，直到0；
那么可以通过该方法来统计第一象限的整数点个数，最后乘上4即可

static void solve() throws IOException {
    long r = pInt();
    long ans = 0;
    long y = r;
    long max = (r + 1) * (r + 1);
    long min = r * r;
    for (long i = 0; i <= r; i ++) {
   		// 找到第一个距离为r+1的点（边界）
        while (i * i + y * y >= max) y --;
        // 此时(i, t)点满足条件
        long t = y;
        while (i * i + t * t >= min && t > 0) {
            ans ++;
            t --;
        }
    }
    out.println(ans * 4);
}

模板代码

import java.io.*;
import java.nio.file.Files;
import java.nio.file.Paths;

public class Example {

    static void solve() throws IOException {

    }

    public static void main(String[] args) throws IOException {
        int t = 1;
//        t = Integer.parseInt(in.readLine());
        while (t -- > 0) {
            solve();
        }
        in.close();
        out.flush();
        out.close();
    }

    private static InputStream is = System.in;
    static {
        try {
            is = Files.newInputStream(Paths.get("F:\\Notes\\Algorithm\\Problems\\java\\java\\src\\main\\java\\input.txt"));
        } catch (Exception e) {
            is = System.in;
        }
    }
    private static final BufferedReader in = new BufferedReader(new InputStreamReader(is));
    private static final PrintWriter out = new PrintWriter(System.out);
    private static int pInt(String s) {
        return Integer.parseInt(s);
    }
    private static int pInt() throws IOException {return Integer.parseInt(in.readLine());}
    private static long pLong(String s) {
        return Long.parseLong(s);
    }
    private static long pLong() throws IOException {return Long.parseLong(in.readLine());}
    private static String[] pStringArray() throws IOException {
        return in.readLine().split(" ");
    }
    private static int[] pIntArray(int start) throws IOException {
        String[] s = pStringArray();
        int[] arr = new int[start + s.length];
        for (int i = start, j = 0; i < arr.length; i++, j ++) {
            arr[i] = Integer.parseInt(s[j]);
        }
        return arr;
    }

    private static long[] pLongArray(int start) throws IOException {
        String[] s = pStringArray();
        long[] arr = new long[start + s.length];
        for (int i = start, j = 0; i < arr.length; i++, j ++) {
            arr[i] = Long.parseLong(s[j]);
        }
        return arr;
    }
}