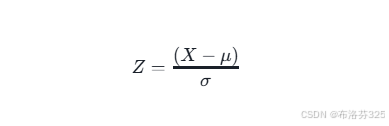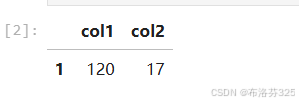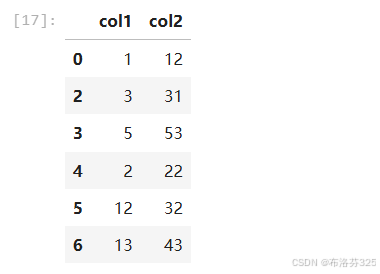Z-score异常值检测法是一种基于统计学原理的异常值检测技术。它通过计算数据点与数据集平均值的标准化距离来判断该数据点是否为异常值。
一、原理
Z-score异常值检测法的原理是基于标准正态分布。它通过计算每个数据点与数据集平均值的差距,并将其转换为标准差的倍数,以此来评估数据点的异常程度。在标准正态分布中,大约68%的数据点位于平均值的一个标准差之内,95%的数据点位于两个标准差之内,而99.7%的数据点位于三个标准差之内。因此,如果一个数据点的Z-score绝对值很大,即它距离平均值很多个标准差,那么它很可能是一个异常值。
Z-score的计算公式如下:
其中:
- 𝑍是数据点 𝑋X 的Z-score。
- 𝑋 是数据集中的某个数据点。
- 𝜇 是数据集的平均值(均值)。
- 𝜎 是数据集的标准差。
通常情况下,有两种常见的阈值选择:
-
阈值 = 2:如果使用Z-score的绝对值大于2作为异常值的判定标准,那么大约有95%的数据将位于这个阈值内,这意味着只有大约5%的数据可能被视为异常值。这是一个相对宽松的阈值,适用于不想过多排除数据点的情况。
-
阈值 = 3:如果使用Z-score的绝对值大于3作为异常值的判定标准,那么大约有99.7%的数据将位于这个阈值内,这意味着只有大约0.3%的数据可能被视为异常值。这是一个更严格的阈值,适用于需要更精确识别异常值的情况。
判断方法:根据公式计算出z分数,然后根据阈值来判断数据点是否为异常值。如果 ∣𝑍∣>阈值则认为该数据点是异常值。
在实际应用中,以下因素可能会影响阈值的选择:
- 数据分布:如果数据非常接近正态分布,可以使用更严格的阈值(如3)。
- 业务需求:在某些业务场景中,可能需要更宽松或更严格的异常值定义。
- 数据量:在大数据集中,使用更严格的阈值可能会导致许多数据点被错误地标记为异常值。
- 异常值的潜在影响:如果异常值对分析结果有重大影响,可能需要使用更严格的阈值。
二、代码实现
import pandas as pd
from scipy.stats import zscore
import numpy as np
# 示例数据
data = {'col1': [1, 120, 3, 5, 2, 12, 13],
'col2': [12, 17, 31, 53, 22, 32, 43]}
df = pd.DataFrame(data)
df
# 计算Z-score
zscore_col1 = zscore(df['col1'])
# 识别Z-score绝对值大于2的异常值
outliers = df[zscore_col1.abs() > 2]
outliers
上述代码输出的是col1列异常值大于2的数据点
# 删除异常值
df_cleaned = df[(np.abs(zscore_col1) < 2)]
# 打印清洗后的数据
print(df_cleaned)Z-score方法缺陷:
- 对正态分布的假设:Z-score方法假设数据服从正态分布。如果数据不服从正态分布,使用Z-score检测异常值可能会产生误导。
- 对极端值的敏感性:如果数据集中存在极端异常值,它们会极大地影响平均值和标准差的计算,从而影响其他数据点的Z-score。
- 阈值的选择:选择合适的阈值是一个主观的过程,不同的阈值会导致不同的异常值检测结果。
- 不适用于小样本数据:在样本量较小的情况下,标准差可能不够稳定,导致Z-score的可靠性降低。
- 无法检测非线性关系:Z-score方法无法检测数据中的非线性关系,例如,数据可能在一个特定的区域内密集,而在另一个区域内稀疏,这种情况下Z-score方法可能无法有效识别异常值。
- 忽略变量间的相关性:在多变量数据集中,Z-score方法没有考虑变量之间的相关性,可能导致误判。
更多内容,请关注下面的公众号