0-1背包问题(动态规划+回溯法)

一、题目

题目内容

给定n(n<=100)种物品和一个背包。物品i的重量是wi(wi<=100)，价值为vi(vi<=100)，背包的容量为C(C<=1000)。
应如何选择装入背包中的物品，使得装入背包中物品的总价值最大? 在选择装入背包的物品时，对每种物品i只有两个选择：装入或不装入。不能将物品i装入多次，也不能只装入部分物品i。

输入格式：

共有n+1行输入：
第一行为n值和c值，表示n件物品和背包容量c；
接下来的n行，每行有两个数据，分别表示第i(1≤i≤n)件物品的重量和价值。

输出格式：

输出装入背包中物品的最大总价值。

输入样例：

输出样例：

二、动态规划解

1、定义dp数组

dp[i][j]来表示在前i个物品中，背包容量为j时能够获得的最大总价值（每一个格子都是最大容量）。

2、初始化

此时很显然，i=0时不放入物品，价值必为零，j=0时，物品无法放入，价值为零

所以i==0或者j==0时，dp[i][j]初始化为0。即表示背包容量为0或没有物品可选时的总价值均为0。

3、状态转移

在每一步计算价值的时候，考虑两种情况：当前物品放入或者不放入背包。

不放入背包：

那么同等重量背包下，价值和i-1时相同，即dp[i][j]=dp[i-1][j].

放入背包：

放入时也有两种情况：容量足够，成功放入；容量不足，无法放入

判断依据为：j-w[i-1]是否大于等于零(w数组为放入的物品重量数组，w[i-1]是第i个物品的重量，下标从零开始；如果下标从1开始，w[i]为第i个物品重量，v数组为放入的物品价值数组，其余同上)。

如果j-w[i-1]<0，说明无法放入这个物品，这时，转为不放入背包的情况。

如果j-w[i-1]>0，说明可以放入这个物品，这时，比较放入的情况和不放入的情况哪一种的物品价值高。放入的情况即为dp[i-1][j-w[i-1]]+v[i-1](dp[i-1][j-w[i-1]]代表着在装入该物品外，剩余容量的装入最大价值情况)，不放入的情况为dp[i-1][j];

状态转移推论：

对于每个物品i（i从1到n）：
        对于每个背包容量j（j从1到C）：
                如果当前物品i的重量小于等于当前背包容量j：
                        dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1])
                        其中dp[i - 1][j]表示不装入第i个物品时的总价值，dp[i - 1][j - w[i - 1]] + v[i - 1]表示装入第i个物品时的总价值。
               如果当前物品i的重量大于当前背包容量j：
                        dp[i][j] = dp[i - 1][j]，不能装入第i个物品，总价值与前i-1个物品时背包容量为j时的总价值相同。

综上所述，在这两种情况下选择最优解，即易得dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i-1]]+v[i-1])

逐步填表：

从左到右，从上到下填充dp数组，根据状态转移方程填写每个dp[i][j]的值。

最终结果：

返回dp[n][C]，即前n个物品在背包容量为C时能够获得的最大总价值。
这样的动态规划方法能够在时间复杂度为O(n*C)的情况下解决0-1背包问题，其中n为物品数量，C为背包容量。

实验代码：

#include <stdio.h>

int max(int a, int b) {
    return (a > b) ? a : b;
}
//比较大小函数

int knapsackMaxValue(int n, int C, int weights[], int values[]) {
    int dp[n + 1][C + 1];

    for (int i = 0; i <= n; ++i) {
        for (int j = 0; j <= C; ++j) {
            if (i == 0 || j == 0) {
                //初始化
                dp[i][j] = 0;
            } else if (weights[i - 1] <= j) {
                //可装入背包
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);
            } else {
                //不可装入背包
                dp[i][j] = dp[i - 1][j];
            }
        }
    }

    return dp[n][C];
}

int main() {
    int n, C;
    scanf("%d %d", &n, &C);

    int weights[n], values[n];

    for (int i = 0; i < n; ++i) {
        scanf("%d %d", &weights[i], &values[i]);
    }

    int result = knapsackMaxValue(n, C, weights, values);
    printf("%d\n", result);

    return 0;
}

三、回溯法

1、基本思路

用一个max记录整个背包中所装物品价值的最大值，将背包里的物品的重量和价值均初始化为0，当背包中已有重量加上当前物品重量未超限时，将该物品放入背包，进入下一次遍历，如果超限，那么直接进入下一件物品的判定，直到最后一件物品判定完毕，完成递归，回到上一层后，将当前物品拿出背包，在重新进入下一件物品的判定。

核心思想其实仍为是否选中该物品，差别在于，动态规划中将第i件物品在剩余容量的最大值存放在数组中，整个dp数组只需要计算一次，时间复杂度为O(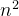 $n^{2}$ )。回溯法，对于每一个物品都由装入和不装入两种情况，每次的剩余容量最大值都需要再次计算，时间复杂度为O( $n^{2}$ )

2、实验代码

#include <stdio.h>
#define N 100

int max = 0;
int n, c;
int weight[N];
int value[N];

void backresult(int index, int currentWeight, int currentValue) {
    if (index == n) {
        if (currentWeight <= c && currentValue > max) {
            max = currentValue;
        }
        return;
    }

    // 选择当前物品
    if (currentWeight + weight[index] <= c) {
        currentWeight += weight[index];
        currentValue += value[index];

        backresult(index + 1, currentWeight, currentValue);

        // 回溯：撤销选择
        currentWeight -= weight[index];
        currentValue -= value[index];
    }

    // 不选择当前物品
    backresult(index + 1, currentWeight, currentValue);
}

int main() {
    scanf("%d %d", &n, &c);

    for (int i = 0; i < n; i++) {
        scanf("%d %d", &weight[i], &value[i]);
    }

    backresult(0, 0, 0);
    printf("%d", max);

    return 0;
}