[高阶数据结构五] 图的遍历和最小生成树

1.前言

本篇文章是在认识图的基础上进行叙述的，如果你还不知道什么是图，图的存储结构。那么请你先阅读以下文章。

[高阶数据结构四] 初始图论-CSDN博客

本章重点：

本篇主要讲解及模拟实现图的遍历算法--DFS和BFS，以及最小生成树算法Kruskal和Prim算法。

2.什么是图的遍历

图的遍历就是，从任意一个顶点开始，可以通过某种方式走过所有的顶点，这就叫做图的遍历。

那么图可以用什么方法来进行遍历呢？之前二叉树的遍历可以通过递归的办法和层序遍历的方法来获取结果，请思考那么图是否也可以使用这种方法呢？---答案是可以的。这就是DFS和BFS

2.1 图的广度优先遍历

先解释什么叫做广度优先遍历：简单来说就是先把一个顶点的相邻朋友顶点全部走完。

例子如下：

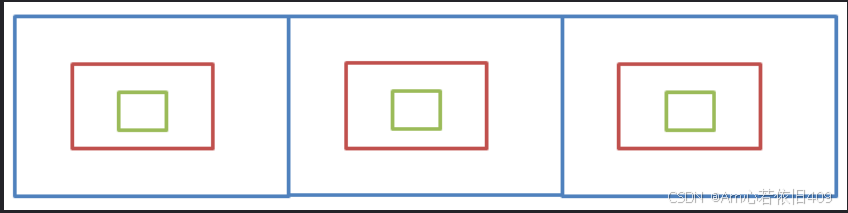
比如现在要找东西，假设有三个抽屉，东西在那个抽屉不清楚，现在要将其找到，广度优先遍历的做法是:

先将三个抽屉打开，在最外层找一遍
将每个抽屉中红色的盒子打开，再找一遍
将红色盒子中绿色盒子打开，再找一遍直到找完所有的盒子

注意:每个盒子只能找一次，不能重复找

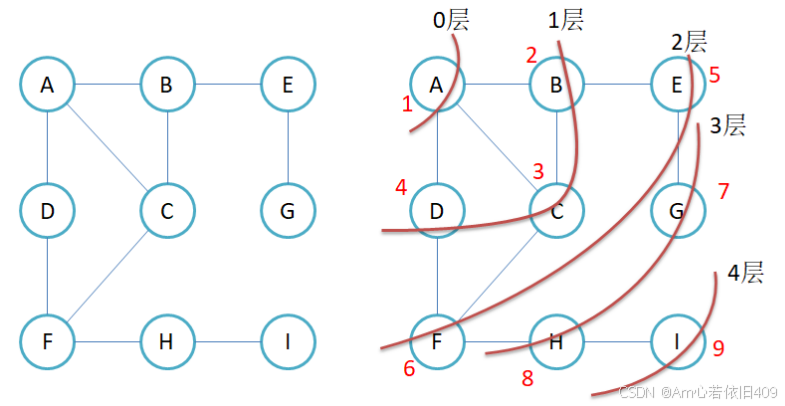
转换到图上面那就是如下情形

模拟一遍过程

假设以A顶点为源点开始遍历，对于顶点A来说, 先走B,C,D. 然后再看B顶点, 走A,C,E, 但是A和C已经走过了,所以不能再此将它们算进去. --那么用什么方法来记录他们是否走过呢？做法很简单, 使用一个visited数组, 数组用来存储一个顶点是否已经入过队列了.

那用什么容器来临时存储这些值呢？--很明显用队列，因为你把A放进容器之后，要判断A的朋友是哪些，然后把A拿出容器，这就联想到了先进先出的情形，所以采用队列这个容器

细节把握清楚了，那么写出代码来就不是很大的问题了。直接上代码

		void BFS(const V& src)//广度优先遍历
		{
			int srci = GetIndex(src);
			if (srci == -1) return;
			vector<bool> visited(_ver.size(), false);
			queue<int> que;
			que.push(srci);
			visited[srci] = true;
			cout << _ver[srci] << " ";
			while (!que.empty())
			{
				int front = que.front();
				que.pop();
				for (int i = 0; i < _ver.size(); ++i)
				{
					if (_martix[front][i] != int_MAX && visited[i] == false)
					{
						que.push(i);
						visited[i] = true;
						cout << _ver[i] << " ";
					}
				}
			}
			cout << endl;
		}

注意：这个代码要和前面的初始图论里面的代码结合起来看，这是在邻接矩阵里面实现的。

2.2 图的深度优先遍历

图的优先遍历就是一条路走到黑，走不通再回退

例子如下：

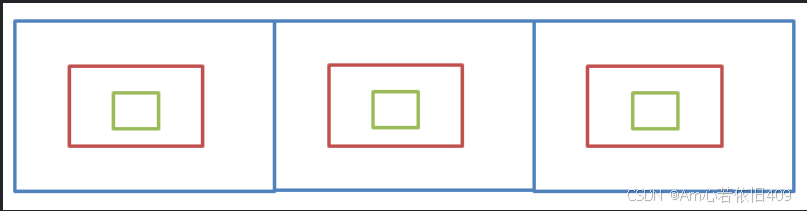
比如现在要找东西，假设有三个抽屉，东西在那个抽屉不清楚，现在要将其找到，广度优先遍历的做法是:

先将第一个抽屉打开，在最外层找一遍
将第一个抽屉中红盒子打开，在红盒子中找一遍
将红盒子中绿盒子打开，在绿盒子中找一遍
递归查找剩余的两个盒子

深度优先遍历:将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子)，再去递归遍历其他盒子

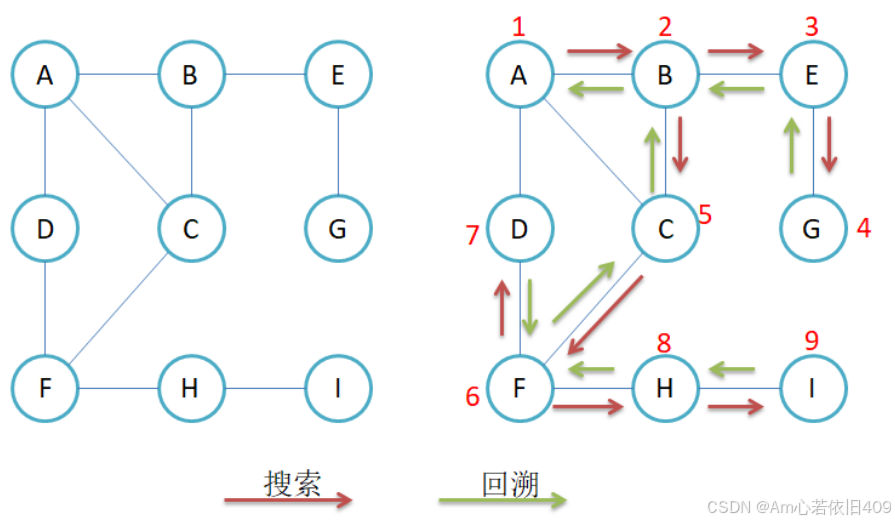
模拟一遍过程：

这之前和树的递归和回溯类似的，代码写起来也很简单

代码如下：

	void _DFS(int index, vector<bool>& visited)
		{
			if (!visited[index])
			{
				cout << _ver[index] << " ";
				visited[index] = true;

				//遍历与这个点所有相邻的点
				for (int i = 0; i < _ver.size(); ++i)
				{
					if (_martix[index][i] != int_MAX && visited[i] == false)
						_DFS(i, visited);
				}
			}
		}
		void DFS(const V& v)//深度优先遍历
		{
			int srci = GetIndex(v);
			if (srci == -1) return;
			vector<bool> visited(_ver.size(), false);
			_DFS(srci, visited);

			//有可能这个图并不是连通的，所以最好都遍历一遍
			for (int i = 0; i < _ver.size(); ++i)
			{
				if (visited[i] == false)
					_DFS(i, visited);
			}
		}

3.图的最小生成树

在讲解最小生成树之前先明确概念。

连通图中的每一棵生成树，都是原图的一个极大无环子图，即： 从其中删去任何一条边，生成树

就不在连通；反之，在其中引入任何一条新边，都会形成一条回路 。

若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

只能使用图中的边来构造最小生成树
只能使用恰好n-1条边来连接图中的n个顶点
选用的n-1条边不能构成回路

最小生成树其实就是子图是最简单的连通图, n-1条边刚好可以连接n个顶点

最小生成树也是图的子图，但是又满足如下的规则：

首先要是一个连通图：那么就表示任意两点间都有路径能去
其次就是不能有环
子图中要包含所有的顶点，且边刚好是n-1条
子图中所有边的权值要是最小

每一个图的最小生成树是不唯一的. 通常有Kruskal算法和prim算法来构造最小生成树

3.1 Kruskal算法

任 给一个有 n 个顶点的连通网络 N={V,E} ， 首先构造一个由这 n 个顶点组成、不含任何边的图 G={V,NULL} ，其中每个顶点自成一个连通分量， 其次不断从 E 中取出权值最小的一条边 ( 若有多条任取其一 ) ，若该边的两个顶点来自不同的连通分 量，则将此边加入到 G 中。如此重复，直到所有顶点在同一个连通分量上为止。

简单来说就是给一个源点，然后先找出与源点相邻的节点，然后源点与这些相邻节点构成的边里面找出最小值，然后在从与选出节点的的相邻的边里面找出最小值，依次迭代。

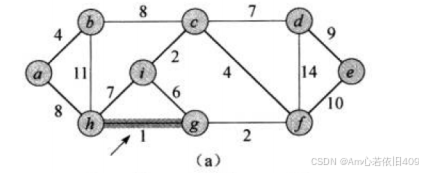
核心思路： 每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树。

外界是要传一棵没有进行初始化的树，以及一个源点，然后从这个源点开始来进行选择。

这个算法的核心就是每次迭代时，找出与其相邻的最小边，那么怎么找最小呢？---那肯定是用优先级队列了，那么还有一个问题就是在你一直选边的过程中，你怎么知道是否构成了环呢？---那么就可以用之前学到过的并查集的思路，判断两个节点是否在一个里面，如果在那么就肯定是环，这条边就不能要，否则就可以要了。

代码如下：

typedef Graph<V, W,int_MAX, Direction> Self;
		struct EDGE
		{
			int _srci;
			int _dsti;
			W _w;
			EDGE(int& srci, int& dsti, W& w) :_srci(srci), _dsti(dsti), _w(w)
			{}
			bool operator>(const EDGE& e) const
			{
				return _w > e._w;
			}
		};
		W Kruskal(Self& MinTree)
		{
			// 最小生成树是每次都找出图中权值最小的边来构造最小生成树
			// 因此使用优先级队列来存储边以及边的两个点，根据权值来进行排序，小的优先级高
			// 并查集来判断是否形成了环--若两个点的公共祖先是同一个，那么肯定形成了环

			//由于传过来的最小生成树是未初始化的，所以要先进行赋值。否则后续使用会出问题
			MinTree._ver = _ver;
			MinTree._umapIndex = _umapIndex;
			MinTree._martix.resize(_ver.size());
			for (auto& e : MinTree._martix)
			{
				e.resize(_ver.size(), int_MAX);
			}
			priority_queue<EDGE, vector<EDGE>, greater<EDGE>> que;
			size_t n = _ver.size();
			for (int i = 0; i < n; i++)
			{
				for (int j = 0; j < n; j++)
				{
					//在无向图中是沿对角线对称，所以只遍历一半即可
					if (i<j&&_martix[i][j] != int_MAX)
						que.push(EDGE(i, j, _martix[i][j]));
				}
			}

			//优先级队列和并查集都准备好了，现在开始往最小树里面添加边了
			W totalweight =W();
			int size = 0;
			UnionFindSet UFS(n);
			while (!que.empty())
			{
				EDGE min = que.top();
				que.pop();
				if (!UFS.SameSet(min._srci, min._dsti))
				{
					//不在一个集合
					cout << _ver[min._srci] << "->" << _ver[min._dsti] << ":" << min._w << endl;
					MinTree._AddEdge(min._srci, min._dsti, min._w);
					UFS.Union(min._srci, min._dsti);
					totalweight += min._w;
					size++;//边数+1
				}
			}
			if (size == n - 1) return totalweight;
			else return W();
		}

上诉代码用的是Greater这个仿函数，以及前面学到的并查集，如果不知道并查集的朋友建议阅读下面这篇文章。

[高阶数据结构(一)]并查集详解-CSDN博客

这里是传入一个空的图，这还是第一次遇见这种写法，以前都是把空间开好，以及初始化好，但是这种写法是非常简洁且相对来说简单的。若还有不懂的欢迎后台TT。

3.2 Prim算法

Prim算法的思想就是从源点开始，每次选择的是找出最小的边。但是与KrusKal算法的区别就是他是从未确定的点里面找出和我当前确定的这个点的最小边。然后依次从未确定的点里面找出所有的边为止。

例如：

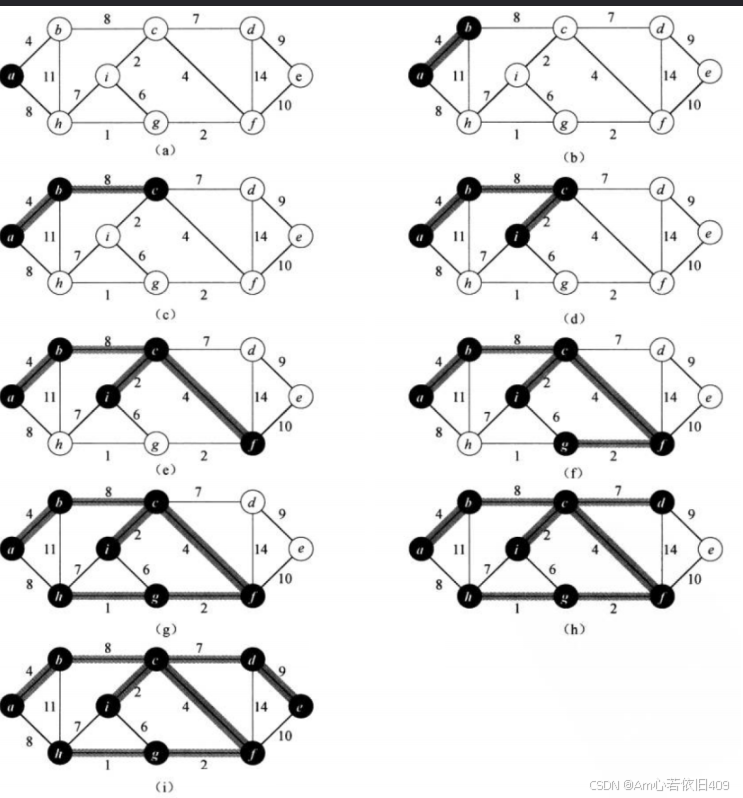
在(a)里面，那么确定的点就是a，不确定的就是b,c,d,e,f,g,i,h。所以从这些点里面，找出与a直接相连构成最小边的点,找出了B。然后确定的点是a,b，所以不确定的点就是c,d,e,f,g,h,i。然后依次类推。这里面也需要判断是否构成环，那么是否构成换还需要像KrusKal算法里面那样，用并查集来判断吗？-----其实是不需要的，因为你这里有两个集合，一个是确定的点，一个是未确定的点，如果选出的两个点都在确定的点里面的话，那么肯定是构成环了，所以肯定是不成立的。那么就需要把这条边pop掉，方便选出后续小的边。

代码如下：

W Prim(Self& MinTree, const V& v)//传过来最小生成树，和开始的起点
		{
			//初始化最小生成树
			size_t n = _ver.size();
			MinTree._ver = _ver;
			MinTree._umapIndex = _umapIndex;
			MinTree._martix.resize(n);
			for (int i = 0; i < n; i++)
				MinTree._martix[i].resize(n, int_MAX);

			//第二步开始存储于起点连接的权值最小的边
			int srci = GetIndex(v);
			priority_queue<EDGE, vector<EDGE>, greater<EDGE>> pque;
			//与srci相连的节点在哪呢？--遍历srci这一行即可
			for (int i = 0; i < n; i++)
			{
				if (_martix[srci][i] != int_MAX)
					pque.push(EDGE(srci, i, _martix[srci][i]));
			}

			//第三步，找两个集合，一个集合是确定是最小生成树的点，一个集和是还没有确定
			vector<bool> X(n, false);
			vector<bool> Y(n, false);
			X[srci] = true;//true表示在这个集合
			for (int i = 0; i < n; i++)
				if (srci != i)
					Y[i] = true;

			W totalweight = W();
			int size = 0;
			//第四步，开始找边
			while (!pque.empty())
			{
				EDGE min = pque.top();
				pque.pop();
				//一条边的起点一定在X里面，只要终点不在的话那就不会构成环了
				if (X[min._dsti])
				{
					cout << "选这条边的话，成环了" << endl;
					cout << "[" << _ver[min._srci] << "]" << "->" << "[" << _ver[min._dsti] \
						<< "]" << ": " << min._w << endl;
				}
				else
				{
					//找到了合适的边
					X[min._dsti] = true;
					Y[min._dsti] = false;
					MinTree._AddEdge(min._srci, min._dsti, min._w);
					cout << "[" << _ver[min._srci] << "]" << "->" << "[" << _ver[min._dsti] \
						<< "]" << ": " << min._w << endl;
					size++;
					totalweight += min._w;
					if (size == n - 1) break;

					//把所有的与min._dsti相连的边放入最小队列
					for (int i = 0; i < n; i++)
					{
						if (X[i] != true && _martix[min._dsti][i] != int_MAX)
							pque.push(EDGE(min._dsti, i, _martix[min._dsti][i]));
					}
				}
			}
			if (size == n - 1) return totalweight;
			else return W();
		}

这个算法和前面的kruskal算法都是用的是贪心的策略，但是唯一不同的就是两者判断环的思路是不一致的，一个借助的是并查集，一个借助的是两个数组。

4.总结

到这里图的遍历和图的最小生成树算法就学完了，如果有不懂的伙伴，欢迎后台TT我哦。