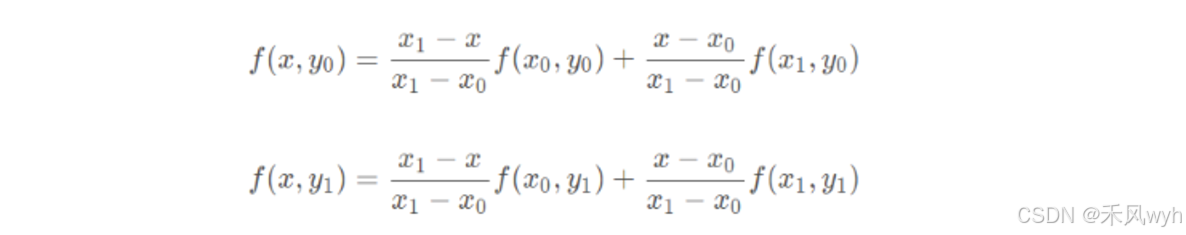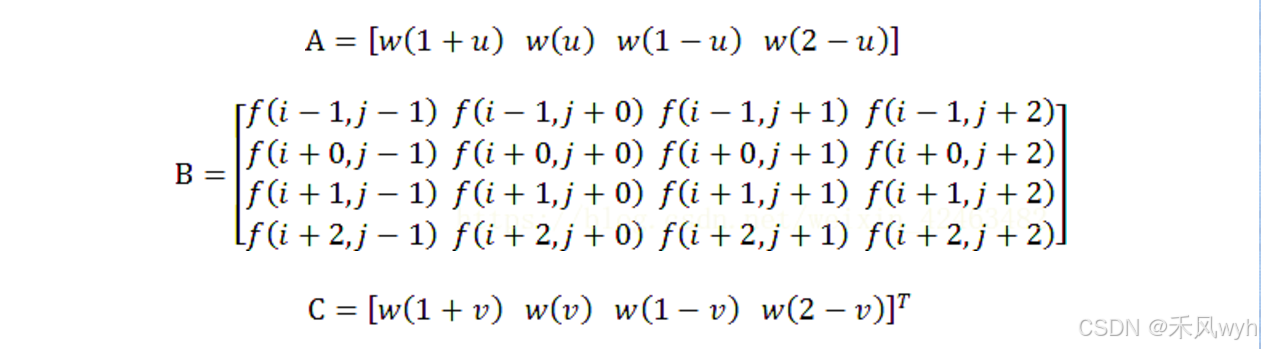上采样(Upsampling)是指通过某些技术手段,将图像、信号或数据的尺寸增加到较大的尺寸。在图像处理中,常常用于生成高分辨率图像,或者增加图像的尺寸以匹配某些网络结构的输入要求,往往我们会采用插值法来实现上采样操作。
在离散数学 中,插值指在离散数据的基础上补插连续函数,使得连续曲线 通过 全部给定的离散数据点。作为离散函数逼近的重要方法,利用插值可根据函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
1. 最近邻插值Nearest Neighbor Interpolation——零阶插值法
最近邻插值是最简单的一种上采样方法,它将目标像素值设为距离该像素最近的源像素值。这种方法计算速度非常快,但可能会导致图像的锯齿感和不平滑效果。
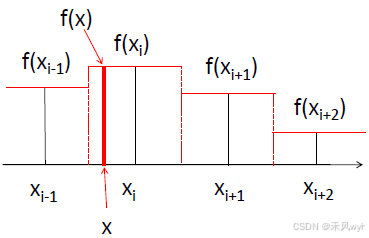
在坐标轴上有一系列的点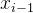
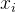
,…,这些点之间的间隔是均匀的(由红色虚线划分)。每个非边界点 xix_ixi 都有一个固定宽度的邻域,由其相邻的点构成。在进行插值时,插值点 x 位于某个邻域内时,插值结果 f(x) 就等于该邻域内最近的原始坐标点
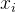
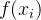
在二维情况下,假设原图像中的四个已知坐标点为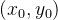
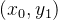
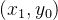
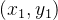
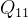
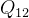
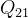
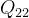
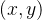
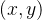
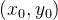
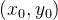
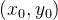
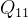
最近邻插值的有优点是速度快,计算量少,适用于实时性要求高的场景。但是其插值后图像可能会非常粗糙,产生较为明显的“块状”效果。
2. 线性插值Linear Interpolation——一阶插值法
线性插值是一种常见的数值插值方法,用于在已知数据点之间估算未知的函数值。其基本思想是通过已知的两个数据点构建一条直线,然后利用该直线来推算未知点的值。
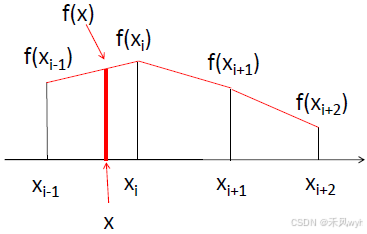
下图展示的是一维线性插值的定性示意图。在坐标轴上,点 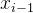
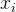
,… 之间的值通过相邻点连线形成线段,构成一个连续的约束函数。对于插值点 x,根据这个约束函数,插值点的值应该为 f(x)。因为每两个坐标点之间的关系是通过一次线性函数(即直线)来表示的,因此插值方法本质上是“线性”的,这就是为什么该方法被称为线性插值。
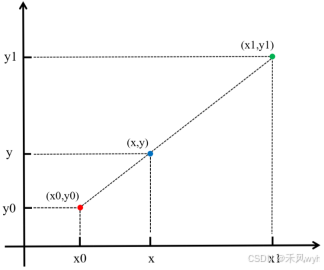
在定量示意图中,设 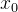
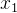
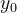
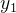
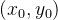
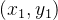
其值可以通过线性插值公式计算得出:
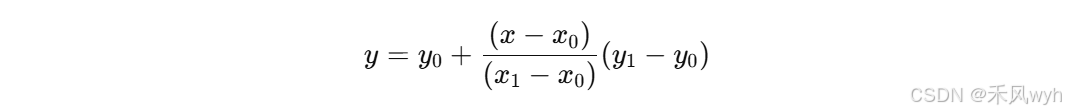
3. 双线性插值法Bilinear Interpolation——一阶插值法
线性插值通过考虑目标像素的上下左右四个邻域像素的加权平均来估算目标像素的值。与最近邻插值相比,双线性插值可以产生更平滑的结果。
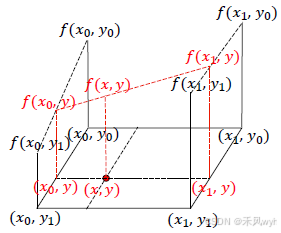
双线性插值可以看作是一维线性插值的扩展,在二维图像中处理时,通常需要经过两步一维线性插值才能得到最终的插值结果。具体来说,给定四个已知像素坐标点: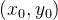
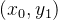
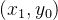
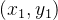
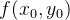
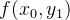
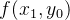
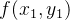
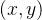
- 首先,在 y 轴方向进行一维线性插值:
- 对于点
和
,计算
;
- 对于点
和
,计算
。
- 对于点
- 然后,在 x 轴方向进行一维线性插值:
- 使用步骤 1 中计算出的
和
,在 x 轴上进行线性插值,得到最终的插值值
。
- 使用步骤 1 中计算出的
另一种做法是先在 x 轴上进行一维线性插值,再在 y 轴上进行一维线性插值,最终结果是一样的,只是插值的顺序不同。
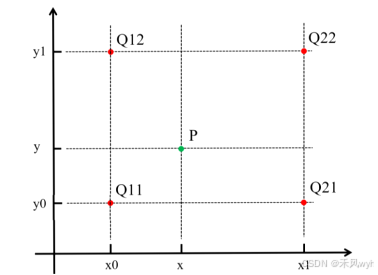
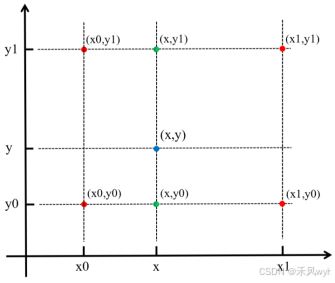
二维双线性插值的定量俯视示意图如下。由像素坐标点 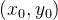
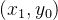
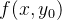
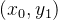
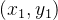
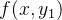
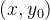
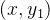
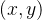
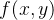
公式如下:

3. 双三次插值Bicubic Interpolation
双三次插值考虑了目标像素周围16个邻域像素的加权平均,使用三次多项式来计算目标像素的值。它比双线性插值提供更高质量的上采样效果,尤其适用于图像边缘和细节较为复杂的情况。 双三次插值又被称为立方卷积插值 / 双立方插值,在数值分析中,双三次插值是二维空间中最常用的插值方法。在这种方法中,插值点 (x, y) 的像素灰度值 f(x, y) 通过矩形网格中最近的十六个采样点的加权平均得到,而各采样点的权重由该点到待求插值点的距离确定,此距离包括水平和竖直 两个方向上的距离。
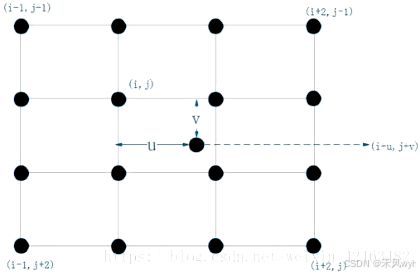
下图是一个二维图像的双三次插值俯视示意图。设待求插值点坐标为 ,已知其周围的 16 个像素坐标点 (网格) 的灰度值,还需要计算 16 个点各自的权重。以像素坐标点
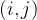
的距离分别为
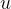
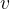
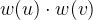
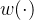
那么,待求插值点 的灰度值
将通过如下计算得到:
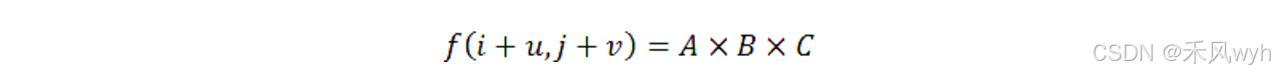
插值权重核 w(·) 为:
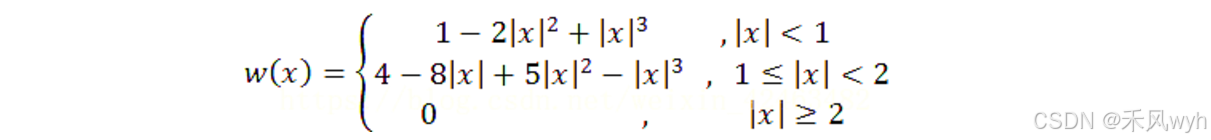
4. 转置卷积(Deconvolution / Transposed Convolution)
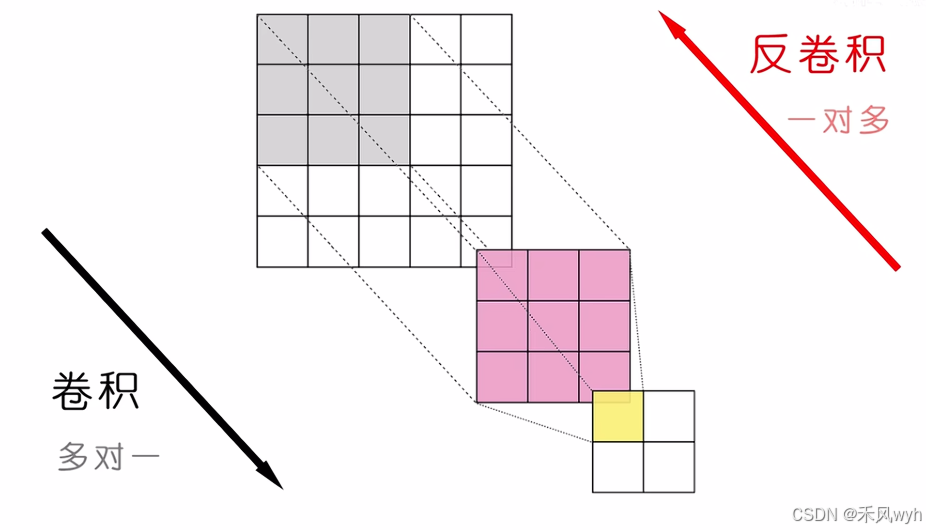
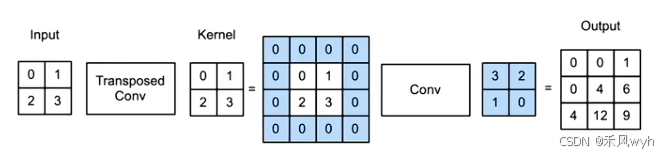
转置卷积是一种神经网络层,转置卷积也被称为反卷积用于通过学习得到一个权重矩阵来进行上采样。这种方法通常用于深度学习模型中,特别是在生成对抗网络(GAN)和自编码器中用于生成高分辨率图像。卷积不会增大输入的高和宽,通常要么不变、要么减半。但是在语义分割这种任务上,仅仅使用卷积无法进行像素级的输出,这时候就可以用到转置卷积来增大输入高和宽。反卷积是卷积的逆操作。
在反卷积进行的时候,也需要滑动操作。将输入图像上的0、1、2、3分别与卷积核进行相乘操作,得到结果后在与输出图像相同尺寸的框图上进行滑动,最终将这些结果进行相加。
为什么反卷积又叫做转置卷积呢?对于一个卷积操作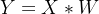
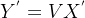
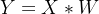
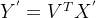
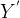
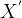
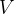
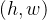
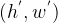
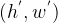
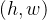
转置卷积也是一种卷积。当填充为0,步幅为1时,将输入填充k-1(k是核窗口),将核矩阵上下、左右翻转,然后做正常卷积(填充0、步幅1),可以得到结果等价于转置卷积。
当填充为p,步幅为1时,将输入填充k-p-1(k是核窗口),将核矩阵上下、左右翻转,然后做正常卷积(填充0、步幅1),可以得到结果等价于转置卷积。
当填充为p,步幅为s时,在行和列之间插入s-1行或列,将输入填充k-p-1(k是核窗口),将核矩阵上下、左右翻转,然后做正常卷积(填充0、步幅1),可以得到结果等价于转置卷积。
转置卷积输出特征图尺寸计算公式如下:
转置卷积能够通过训练获得最佳的上采样结果,并能有效保留图像的细节。但需要大量的数据和计算资源进行训练,可能会导致伪影(比如棋盘状的伪影)。
5. 插值卷积(Subpixel Convolution / Pixel Shuffle)
插值卷积通过像素重排技术,将低分辨率图像的多个通道的像素信息重新排列成一个高分辨率图像。Pixel Shuffle的核心思想是将不同通道的像素按某种规则重新排列,完成上采样。
插值卷积的优点是效果好,能够保持高质量的细节,特别适合用于超分辨率任务,但需要较高的计算能力,适合在深度学习中使用。
6. 零填充(Zero Padding)
零填充是将图像周围的区域填充为零,从而扩大图像的尺寸。这种方法通常作为卷积神经网络(CNN)中的一个步骤,确保在卷积运算后不会丢失信息。
它的优点是操作简单,计算效率高。但是插值效果较差,填充区域的像素会影响最终结果。
7. 多项式插值(Polynomial Interpolation)
通过构造一个多项式来拟合数据点,进而计算目标像素值。这种方法能够提供较为平滑的插值效果。
优点是插值效果较好,适合较为复杂的图像。但是计算量较大,处理速度较慢。
参考资料:
【图像处理】详解 最近邻插值、线性插值、双线性插值、双三次插值-CSDN博客