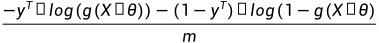多类别逻辑回归

使用机器学习对图片进行分类预测，主要是要通过某种机器学习算法，对大量已知图片数据进行训练，得出相应的假设公式。具体来说，可分为下列步骤：

准备训练数据
为了使机器学习具有一定的准确性，需要提供足量的训练数据。本例中，我们准备提供0~9这10个数字的手写图片总共5000张(另有500张测试图片)，并且：

每张图片都已经标记好其对应的数字值（称为“分类标签”或Label）

为了便于计算机统一处理，每张图片都是28x28像素

每张图片都是灰度图（即：每个像素的取值从0~255，0为白色，255为黑色），这样就省去了处理RGB彩色的负担

上述所有训练样本数据已经存放在【digits_training.csv】中，测试样本数据都存放在【digits_testing.csv】中

准备好训练数据的特征值矩阵

对于一张图片，我们准备一个一维数组，将该图片对应的数字(Label)放在数组的第一个元素；然后将图片中每个像素点的值，按行依次连续存放在数组后面的元素中。最终该数组的共有1+28x28=785个元素

将这5000张图片的数据放置在一个二维数组中，容量是：5000x785。这样就构成了一个训练矩阵。

因为像素值在0~255之间，跨度较大，因此必须对训练数据进行归一化(Normalization)

在本例中，我们直接从灰度图像素中提取特征值，这是最简单的提取方法

使用逻辑回归进行分类

有了特征值和Lable矩阵，就可以使用某种机器学习算法进行训练了。

逻辑回归能够较好的进行分类。但是上一章讲的逻辑回归只能分成两个类别。因此需要考虑如何将2-Classes的分类扩展到N-Classes的分类

使用得到的假设公式进行预测

训练完成后，就得到了假设公式

将待预测的图片（也必须是28x28的灰度图），读取到一个一维数组中(784个元素，没有Label）。然后就可以代入到假设公式中进行预测。预测的结果应该能告知是0~9中的哪个数

使用测试数据进行验证

为了判断该假设公式的有效性，需要另外找一批图片（本例中500张）进行验证。

测试数据也需要先进行归一化处理

本例仅统计出预测正确的图片数量占总图片数量的比重（正确率）

上述分析中，最困难的是第3步。因为目前尚不知晓如何进行N-Classes的分类

使用LogisticRegression多分类模型

创建LogisticRegression对象时，请尽量指定multi_class=‘multinomial’ 属性

可先对数据进行归一化处理，能够在一定程度上有利于正确率

如果Feature矩阵X中各元素的值较大，那么 $\text{[math]}$ 的结果也会比较大，从而使成本函数溢出。因此，有必要对X进行归一化处理，减小元素值域范围

可以使用 $\text{[math]}$ 方法来进行归一化，其中 $\text{[math]}$ 是第i个Feature列向量， $\text{[math]}$ 是第个i个Feature的平均值， $\text{[math]}$ 是第个Feature的标准差。但是，在本例中， $\text{[math]}$ 有可能为0，从而没有意义

考虑到灰度图每个像素的最大值就是 $\text{[math]}$ ，因此本例直接使用，这样每个特征值都在[-1,1]之间

注意测试数据也需要进行归一化处理，而且应使用训练数据的参数进行归一化

可以直接应用SVM线性分类器或Softmax分类器

''' 使用LogisticRegression识别手写数字图片 '''

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression

def normalizeData(X, col_avg):
    return (X - col_avg) / 255

trainData = np.loadtxt(open('digits_training.csv', 'r'), delimiter=",",skiprows=1)  # 28X28X1
MTrain, NTrain = np.shape(trainData)
xTrain = trainData[:,1:NTrain]
xTrain_col_avg = np.mean(xTrain, axis=0)
xTrain = normalizeData(xTrain, xTrain_col_avg)         
yTrain = trainData[:,0]
print("装载训练数据：", MTrain, "条，训练中......")

model = LogisticRegression(solver='lbfgs', multi_class='multinomial', max_iter=500) 
model.fit(xTrain, yTrain)

print("训练完毕")
testData = np.loadtxt(open('digits_testing.csv', 'r'), delimiter=",",skiprows=1)
MTest,NTest = np.shape(testData)
xTest = testData[:,1:NTest]
xTest = normalizeData(xTest, xTrain_col_avg)    # 使用训练数据的列均值进行处理
yTest = testData[:,0]
print("装载测试数据：", MTest, "条，预测中......")

yPredict = model.predict(xTest)
errors = np.count_nonzero(yTest - yPredict)
print("预测完毕。错误：", errors, "条")
print("测试数据正确率:", (MTest - errors) / MTest)

使用1 vs All逻辑回归算法

该算法实际上行要对0~9十个数字分别进行逻辑回归。假设Feature矩阵为(5000行x768=28x28列)，Label矩阵为(5000行x1列)。

计算方法

对数字0进行计算时，Feature矩阵中所有不是数字0的样本行，在中对应的值全设为0；否则设为1。也就是说仅仅对0和非0两类数字进行逻辑回归分类。这将得到第1个判别式(共768+1个权重参数)

对数字1进行计算时，Feature矩阵中所有不是数字1的样本行，在中对应的值全设为0；否则设为1。即仅对1和非1两类样本进行逻辑回归分类。得到第2个判别式

依次类推，对于每个数字，都需要生成一个判别式，共有10组。最后产生的矩阵(10行x769列)，每行代表对应数字的判别式参数

预测新图片时，分别使用每个假设函数依次对图片进行预测，得到10个可能性值，分别对应0~9这10种数字的可能性。可能性最高的那个值，就是其对应的数字

关于成本函数的计算

逻辑回归计算中，很容易造成成本函数溢出(NaN)。主要是因为成本函数中有这样一项(X是Feature矩阵)： $\text{[math]}$

如果 $\text{[math]}$ ，那么 $\text{[math]}$ 将会是NaN；如果 $\text{[math]}$ ，那么 $\text{[math]}$ 将会是NaN

根据Sigmoid函数的定义和图像，可以大致估算出，如果 $\text{[math]}$ 的值大于10或小于-10，则 $\text{[math]}$ 将会趋近于1或0

因此，为保证没有溢出，需要尽可能限制的大小范围在之间

下面的例子演示了如何实现1 vs All的算法：

''' 多分类逻辑回归(1vsAll方式)：识别手写数字图片 '''
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt

def normalizeData(X, col_avg):
    return (X - col_avg) / 255

def sigmoid(z):
    return 1. / (1 + np.exp(-z))

def costFn(theta):
    temp = sigmoid(xTrain.dot(theta))
    origin = (-yTrainForSingleLabel.dot(np.log(temp)) - 
        (1 - yTrainForSingleLabel).dot(np.log(1 - temp))) / ROW_COUNT 
    penalty = LAMBDA * np.sum(theta[1:] ** 2) / (2*ROW_COUNT)
    return origin + penalty

def gradientFn(theta):
    originGradient = xTrain.T.dot(sigmoid(xTrain.dot(theta)) - yTrainForSingleLabel) / ROW_COUNT
    penaltyGradient = np.hstack((np.array([0]), LAMBDA * theta[1:])) / ROW_COUNT
    return originGradient + penaltyGradient

trainData = np.loadtxt(open('digits_training.csv', 'r'), delimiter=",",skiprows=1)
MTrain, NTrain = np.shape(trainData)
LAMBDA = 1
FEATURE_COUNT = NTrain             # 含Intercept Item
ROW_COUNT = MTrain
K = 10                             # 分类数目
xTrain = trainData[:,1:NTrain]
xTrain_col_avg = np.mean(xTrain, axis=0)
xTrain = normalizeData(xTrain, xTrain_col_avg)     # 务必对训练数据进行Normalizing，否则很难收敛
x0 = np.ones(MTrain)
xTrain = np.c_[x0, xTrain]         # 增加Intercept Item
yTrain = trainData[:,0].astype(int)
print("装载训练数据：", MTrain, "条，训练中......")

np.random.seed(0)
thetas = np.zeros((K, FEATURE_COUNT))      # 每个Label对应的theta作为一行；共K行
# 注意此处乘以0.01，是为了设法减小xTrain*theta的值，防止sigmoid(xTrain*theta)=0或1，导致log计算溢出
init_theta = np.random.random(FEATURE_COUNT) * 0.01     # 随机初始化theta
yTrainForSingleLabel = np.zeros((ROW_COUNT))
for labelValue in np.arange(0, K):    # 分别为每个Label计算theta
    # 如果yTrain中值与对应labelValue值相同，则为1，否则为0
    yTrainForSingleLabel = (yTrain == labelValue).astype(int)   # astype(int)将True/False转为1/0
    result = opt.minimize(costFn, init_theta, method='BFGS', jac=gradientFn, options={'disp': True})
    print("类别【", labelValue, "】计算完成，结果是：", result.message)
    thetas[labelValue] = result.x

print("训练完毕")
testData = np.loadtxt(open('digits_testing.csv', 'r'), delimiter=",",skiprows=1)
MTest,NTest = np.shape(testData)
xTest = testData[:,1:NTest]
xTest = normalizeData(xTest, xTrain_col_avg)     # 对测试数据也需要Nomalizing
x0 = np.ones(MTest)
xTest = np.c_[x0, xTest]         # 增加Intercept Item
yTest = testData[:, 0].astype(int)
print("装载测试数据：", MTest, "条，预测中......")

temp = xTest.dot(thetas.T)
# MTest x K矩阵。每行代表一条预测结果，该预测结果依次是分类为1、2、3...K的可能性
predicts = sigmoid(xTest.dot(thetas.T))
yPredict = predicts.argmax(axis=1)     # 每行的最大值对应的下标索引，该索引就是其对应的阿拉伯数字

errors = np.count_nonzero(yTest - yPredict)
print("预测完毕。错误：", errors, "条")
print("测试数据正确率:", (MTest - errors) / MTest)

多类别逻辑回归

使用LogisticRegression多分类模型

使用1 vs All逻辑回归算法

悦读