数据结构--二叉树的顺序结构及实现

文章目录

前言
堆

前言

普通的二叉树是不适合用数组来存储的，因为这样会存在大量的空间浪费，但是完全二叉树却更适合用顺序结构存储。

堆

堆的概念以及结构

堆的概念
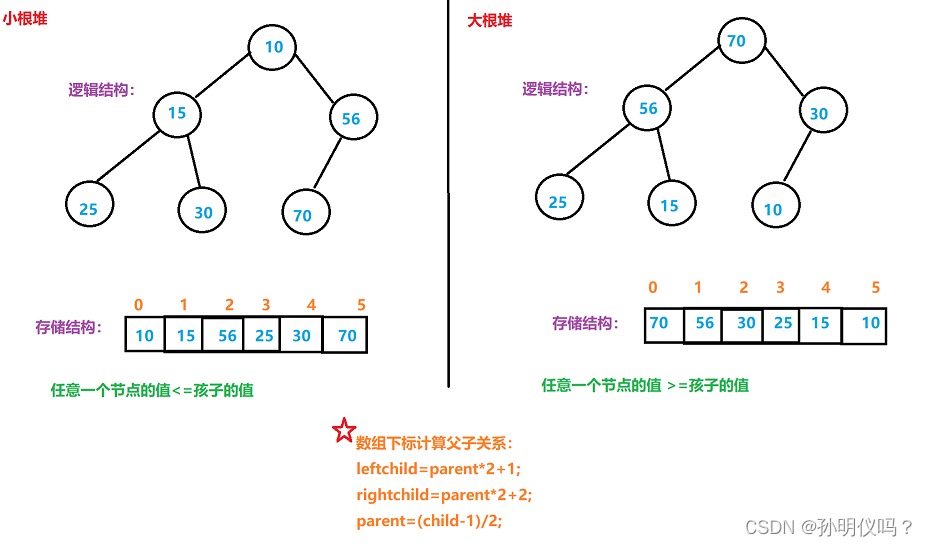
堆是一种二叉树，可以用顺序结构的数组来存储。（这里的堆和操作系统的虚拟进程地址空间的堆不一样，一个是数据结构一个是操作系统的管理内存的一块区域分段）
把所有元素按完全二叉树的顺序存储方式存储在一个一维数组中。

堆的性质
1.堆的某个节点的值总是不大于或者不小于其父节点的值；
2.堆是一棵完全二叉树；

根节点最大的堆叫做最大堆或者大根堆，根节点最小的堆叫做最小堆或者小根堆。

堆的结构
在这里插入图片描述

堆的搭建

1.向上调整创建堆


void AdjustUp(HPdatatype *a,int child)//小堆
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] > a[child])
			{
				Swap(&a[parent], &a[child]);
				child = parent;
				parent = (child - 1) / 2;
			}
		else
		{
			break;
		}
	}
}
void Heapbuild1(int *a,int n)//直接就是对a数组进行建堆打印
{								//向上建堆
	for (int i = 1;i < n;i++)//一开始让第0个成为堆
	{
		AdjustUp(a, i);//每给一个下标数，就相当于后接的数，依次向上调整成堆
	}//建堆
}

2.向下调整建堆

向下调整有个前提：左右子树必须是一个堆

void AdjustDown(HPdatatype* a,int parent,int n)//小堆
{
	HPdatatype minchild = parent * 2 + 1;
	while (minchild < n)//最小孩子没超出范围时
	{
		if (minchild+1<n&&(a[minchild + 1] < a[minchild]))
			{
				minchild++;
			}
		if (a[parent] > a[minchild])
		{
			Swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void Heapbuild2(int* a, int n)//向下调整建堆
{
	for (int i = (n - 1 - 1) / 2;i >= 0;i--)//从最后一个节点的父亲开始，再去减减 调整
	{
		AdjustDown(a, i, n);
	}
}

注意：，一开始要从最后一个节点的父亲开始，以它为父节点，左右子树满足堆，然后向下调整，让这个小子树为堆，最后对当前的parent减减，在去不断让子树成堆，parent不断向上，最后整体也就建成了堆。

比较两种建堆的时间复杂度
1.向上调整建堆
时间复杂度 O（N*logN）
节点越多，调整越多。
有N个数，每次向上调整时间复杂度为 O（logN）（大概为2^k=N）
2.向下调整建堆
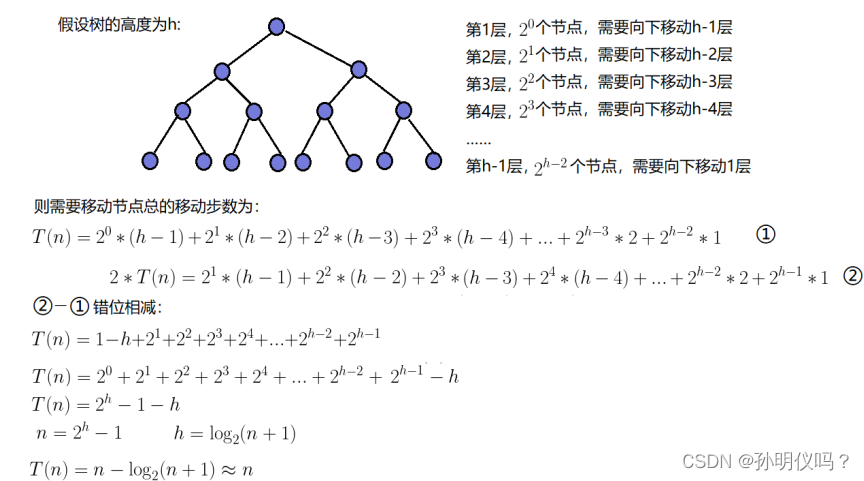
时间复杂读 O（N）
节点越多，调整的越少
（最后一层节点数量2^k-1(假设是满的)，都快等于总节点数量了2^k-1几乎一半了，然而向下调整建堆却不从最后一层开始）
证明：
在这里插入图片描述
利用错位相减得，时间复杂度为O（N）.
综上，建堆最好用向下建堆法！

堆的实现

头文件

typedef int HPdatatype;
typedef struct
{
	HPdatatype* a;
	int size;
	int capacity;

}Heap;

void HeapInit(Heap*hp);
void HeapDestory(Heap* hp);
void HeapPush(Heap* hp, HPdatatype x);
void HeapPop(Heap* hp);
HPdatatype HeapTop(Heap* hp);
int HeapSize(Heap* hp);
bool HeapEmpty(Heap* hp);
void AdjustUp(HPdatatype* a, int child);
void AdjustDown(HPdatatype* a, int parent, int n);
void Swap(HPdatatype* a, HPdatatype* b);
void HeapPrint(Heap* hp);

函数定义

初始化
与顺序表的类似

void HeapInit(Heap* hp)//初始化
{
	assert(hp);
	hp->a = NULL;
	hp->capacity = hp->size = 0;
}

销毁

void HeapDestory(Heap* hp)//销毁
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capacity = hp->size = 0;
}

插入数据
与顺序表一样，先判断是否要扩容，然后把插入的数据放在数组的最后，再去向上调整

void AdjustUp(HPdatatype *a,int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] > a[child])
			{
				Swap(&a[parent], &a[child]);
				child = parent;
				parent = (child - 1) / 2;
			}
		else
		{
			break;
		}
	}
}
void Swap(HPdatatype* a, HPdatatype* b)
{
	HPdatatype c = 0;
	c = *a;
	*a = *b;
	*b = c;
}
void HeapPush(Heap* hp, HPdatatype x)//插入数据
{
	assert(hp);
	if (hp->capacity == hp->size)
	{
		int newCapacity = hp->capacity == 0 ? 4 :hp-> capacity * 2;
		HPdatatype* new = (HPdatatype*)realloc(hp->a, sizeof(HPdatatype) * newCapacity);
		if (new == NULL)
		{
			perror("realloc fail:");
			exit(-1);
		}
		hp->a = new;
		hp->capacity = newCapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size-1);
}

删除数据
在顺序表里，删除就是size–；但是在堆里，删除的是堆顶的元素。
这里的算法是，1.先将堆顶元素和最后一个元素互转，2.然后size–，3.最后把堆顶那个数向下调整。

void AdjustDown(HPdatatype* a,int parent,int n)
{
	HPdatatype minchild = parent * 2 + 1;
	while (minchild < n)//最小孩子没超出范围时
	{
		if (minchild+1<n&&(a[minchild + 1] < a[minchild]))
			{
				minchild++;
			}
		if (a[parent] > a[minchild])
		{
			Swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(Heap* hp)// 删除堆顶元素
{
	assert(hp);
	assert(!HeapEmpty(hp));
	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a,0,hp->size);
}

返回堆顶元素

HPdatatype HeapTop(Heap* hp)//返回堆顶元素
{
	assert(hp);
	assert(!HeapEmpty(hp));
	return hp->a[0];
}

返回堆的数量

int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size - 1;
}

判断堆是否为空

bool HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

打印

void HeapPrint(Heap* hp)
{
	assert(hp);
	for (int i = 0;i < hp->size;i++)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}

主函数

int main()
{
	Heap hp;
	HeapInit(&hp);//创建结构体变量再去初始化，把数组a的值一个个传过去malloc建堆
	int a[] = { 18,15,17,56,28,1,65,38,27,37 };
	for (int i = 0;i < sizeof(a) / sizeof(int);i++)
	{
		HeapPush(&hp, a[i]);
	}
	HeapPrint(&hp);
	HeapPush(&hp, 10);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	//打印也可以
	while (!HeapEmpty(&hp))
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}
	return 0;
}

但是调用print函数和不断top返回数据，打印出来是不一样的。
不断的top 会不断返回完后再去调整成新堆，顺序和之间print的不一样。