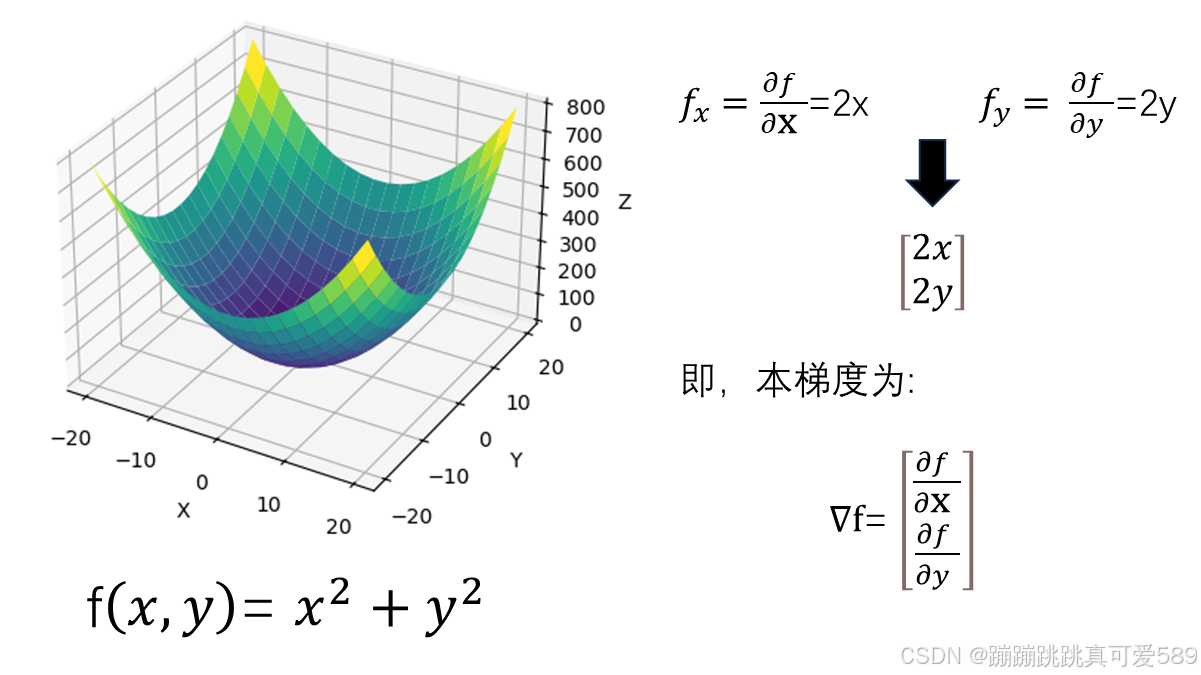
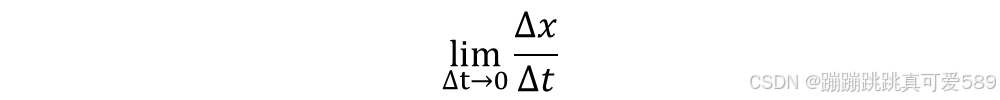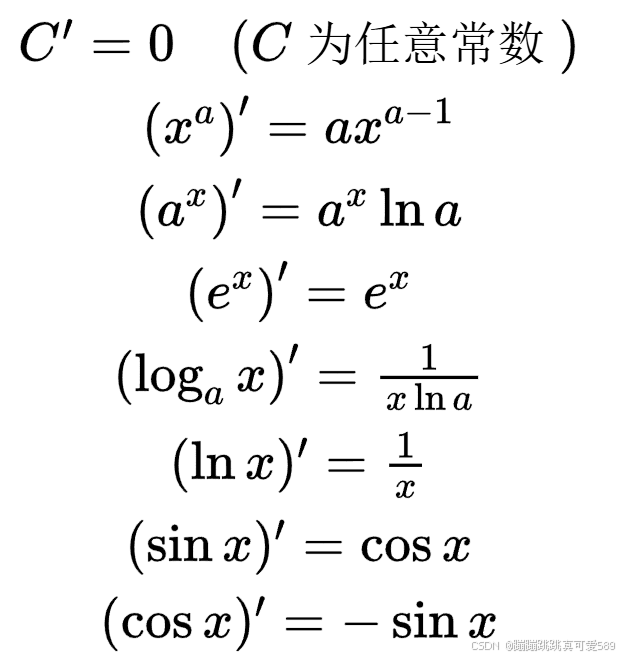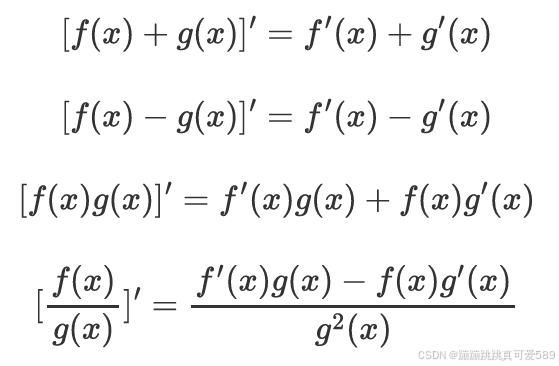一、导数
1.1、导数的定义
注意
- 导数反映了函数相对于自变量变化而变化的快慢程度,即函数的变化率
- 函数f(x)在点x~0~处的导数f'(x~0~)就是导函数f'(x)在点x=x~0~处的函数值
1.2、左导数和右导数
根据从某一点处左右两侧趋近于该点的方向,可以得出左导数和右导数的概念
- 从点x~0~的左侧趋近于x~0~,得到的导数为点x~0~的左导数
- 从点x~0~的右侧趋近于x~0~,得到的导数为点x~0~的右导数
例如:
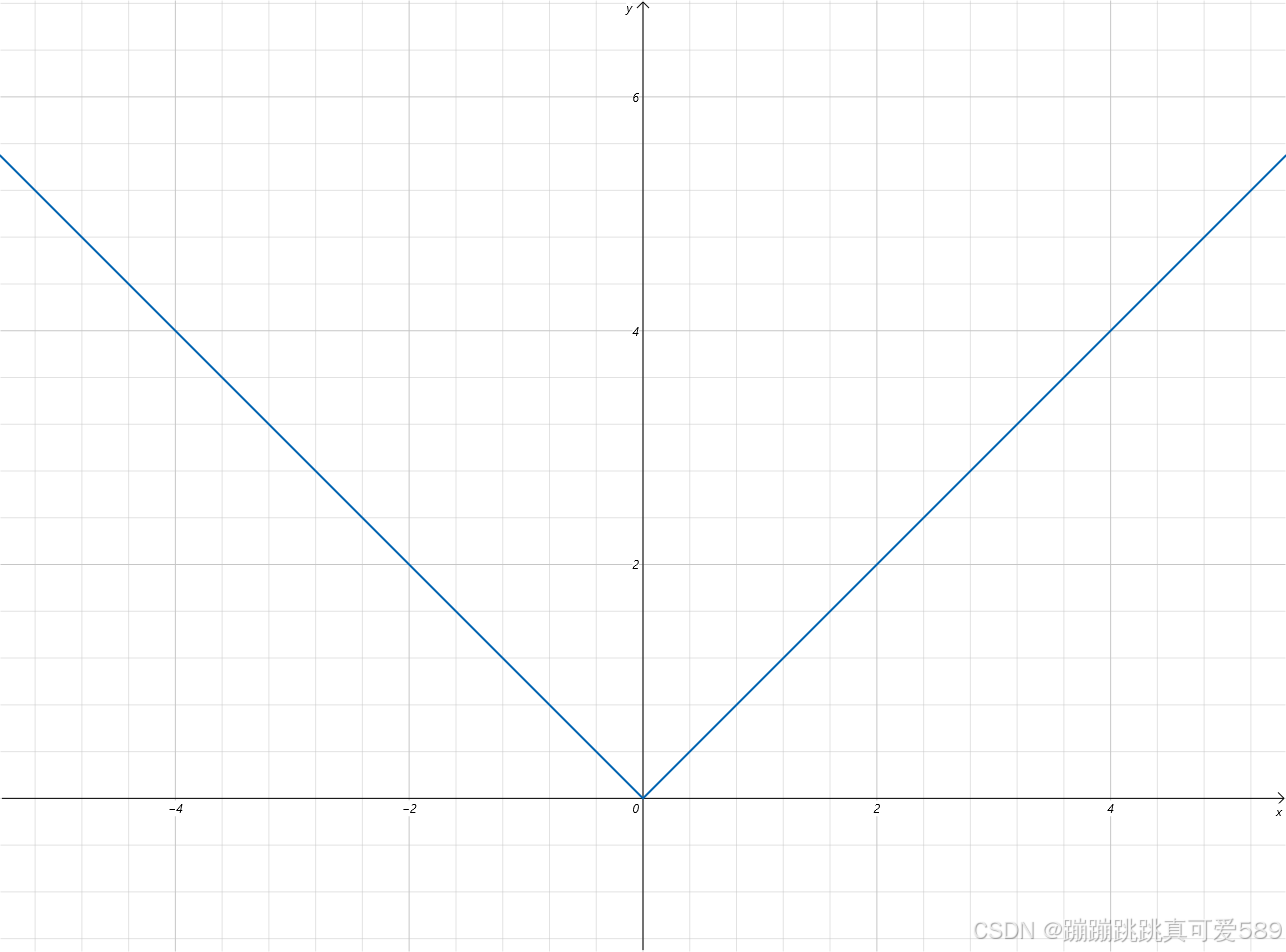
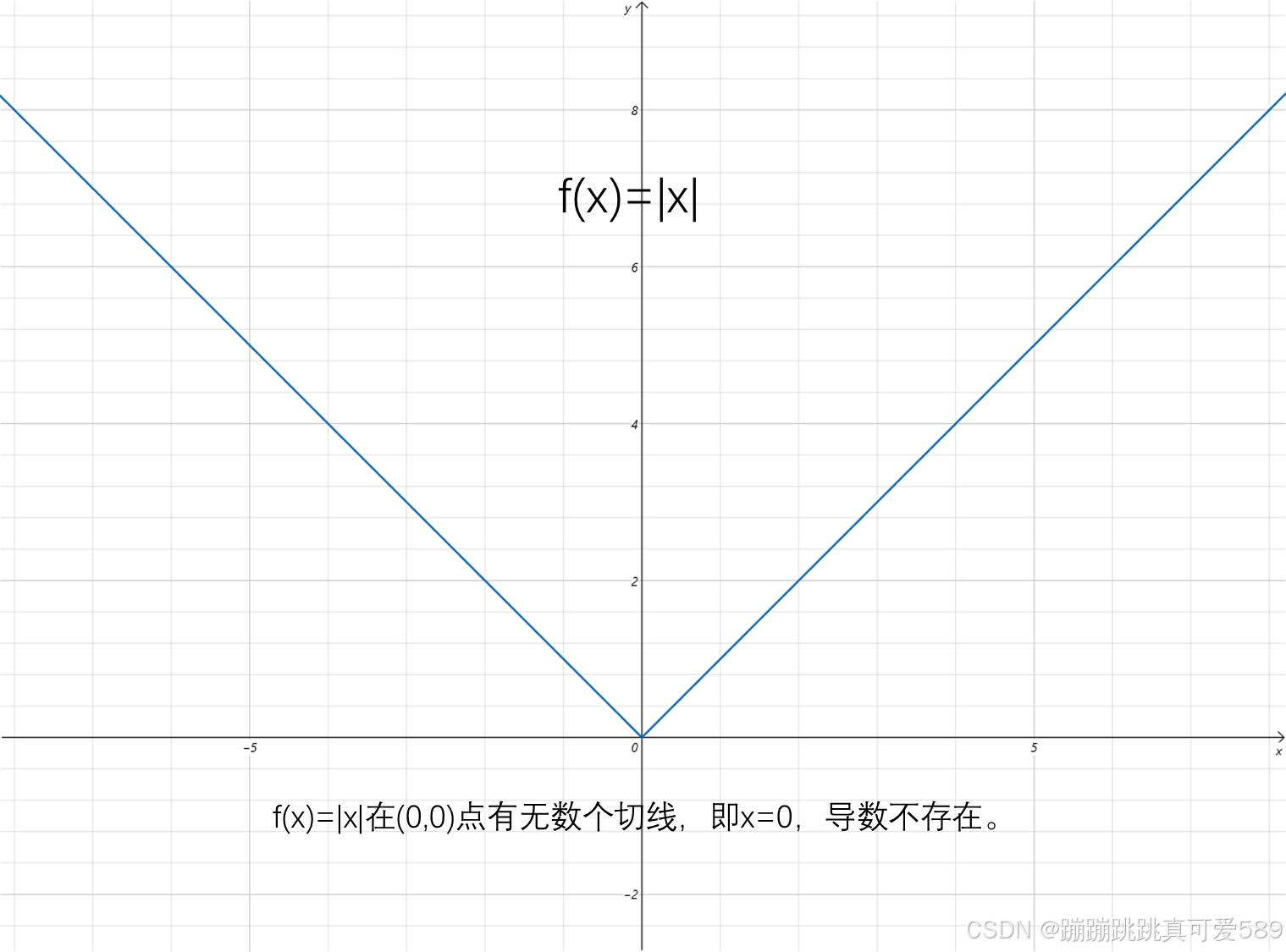
下面的绝对值函数在0点的左导数和右导数不相同,一个-1 一个+1,0 位置不可导
f(x)=|x|
注意
函数y=f(x)在某一点处可导的充分必要条件是y=f(x)在这一点处左、右导数存在且相等。
二、导数的几何意义和物理意义
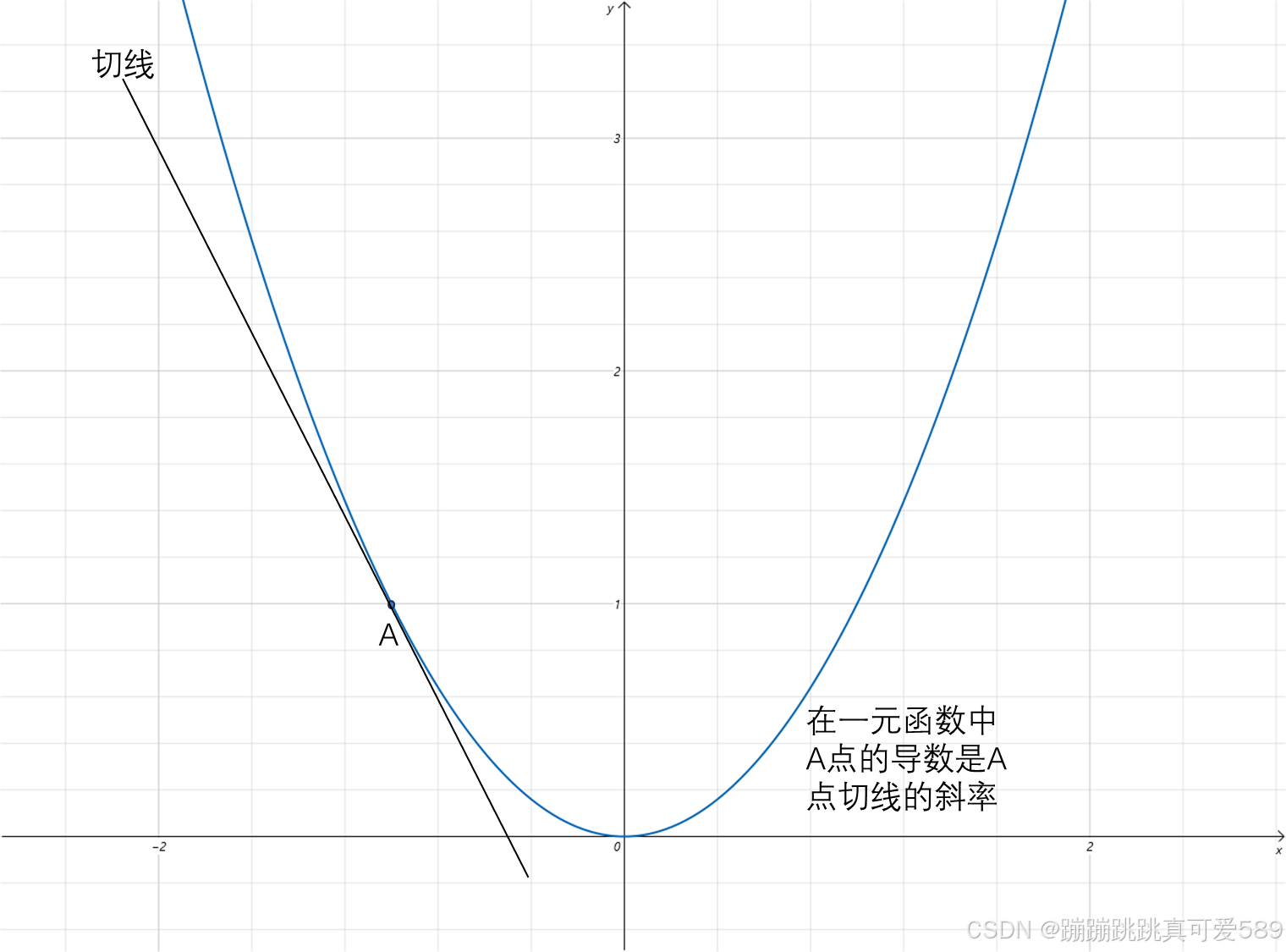
2.1、几何意义——切线的斜率
曲线y=f(x)在点A处切线的斜率就是函数f(x)在点A处的导数
2.2、物理意义——瞬时速度
(小车在马路上匀速的前进):
一段路程共900m,小车匀速走了30s。 在17.5s时,小车运动多快?
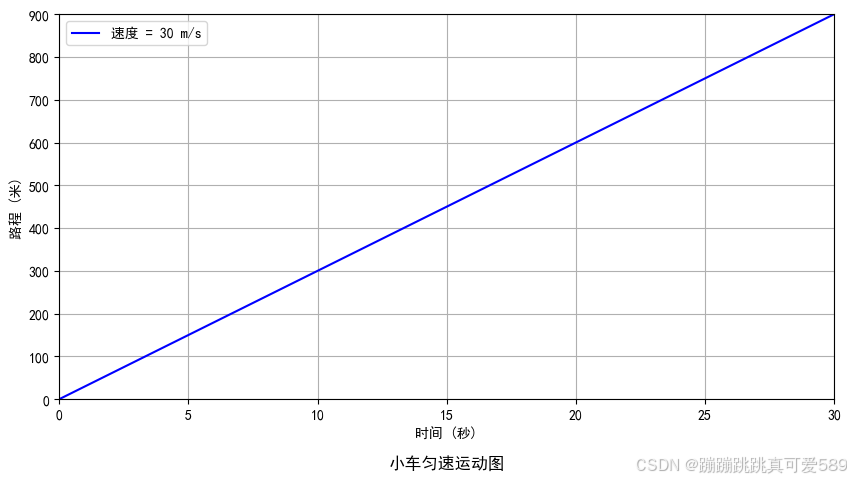
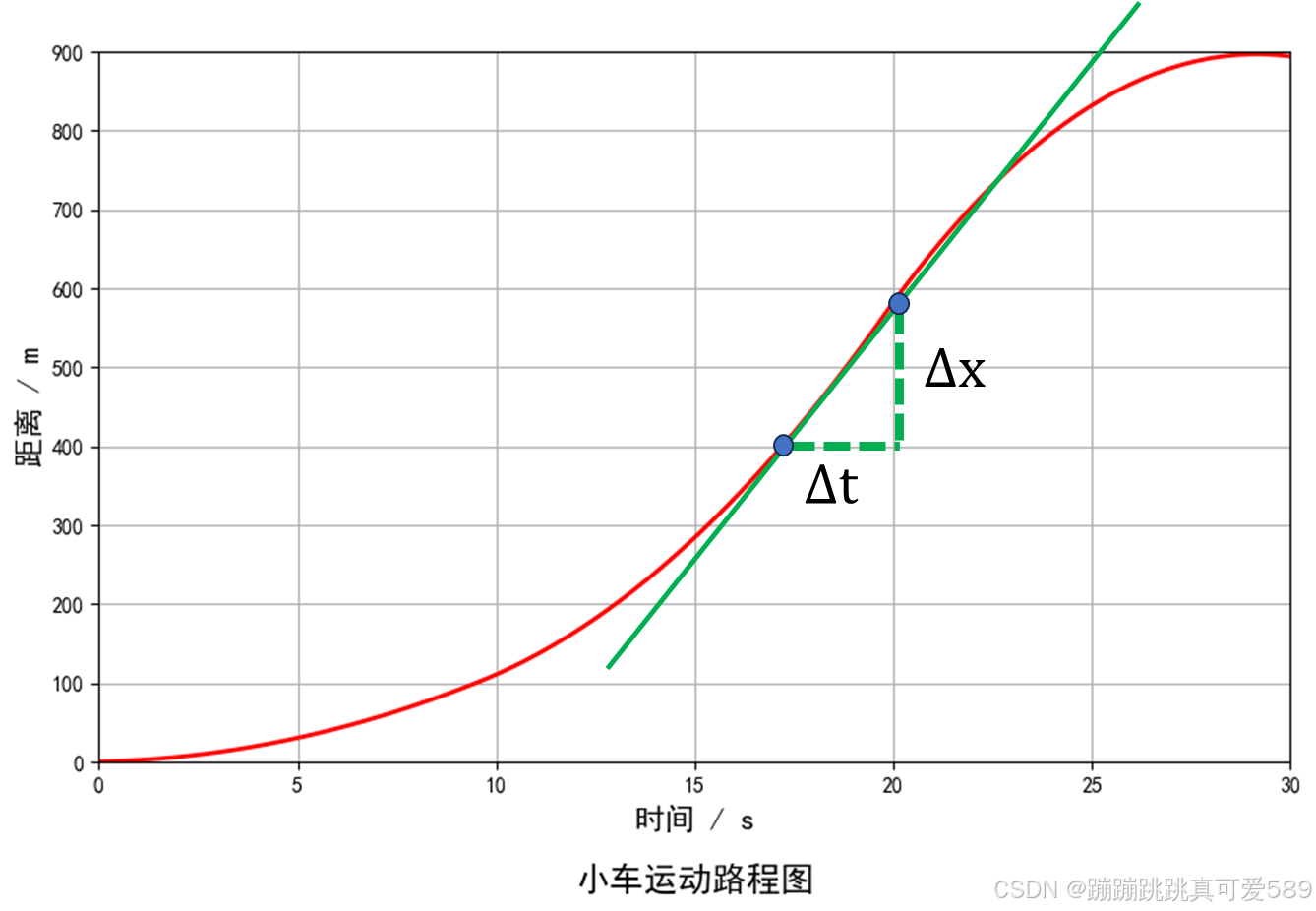
(小车在马路上非匀速的前进): 一段路程共900m,小车不匀速走了30s。 在17.5s时,小车运动多快? 我们就需要求得小车的瞬时速度.
如果物体按x=f(t)的规律做变速直线运动,则在某一刻的瞬时速度即为函数在该时刻的导数
三、基本初等函数导数公式
把常值函数、幂函数、指数函数、对数函数、三角函数、反三角函数这6类函数统称为
基本初等函数。
- 常值函数:y=C, 其中C为常数
- 幂函数:y=x^μ^(其中μ为任意实常数)
- 指数函数:y=a^x^ (a>0且a≠1)
- 对数函数:y=log~a~x (a>0且a≠1)
- 三角函数:如y=sinx,y=cosx,y=tanx,y=cotx等
- 反三角函数:如y=arcsinx,y=arccosx,y=arctanx,y=arccotx
常用基本初等函数导数公式:
四、函数的求导法则
4.1、普通函数求导
4.2、复合函数求导
五、高阶导数与导数判断单调性
5.1、高阶导数
对导数再次求导就是高阶导数,二阶和二阶以上的导数统称为高阶 导数
5.2、导数判断单调性
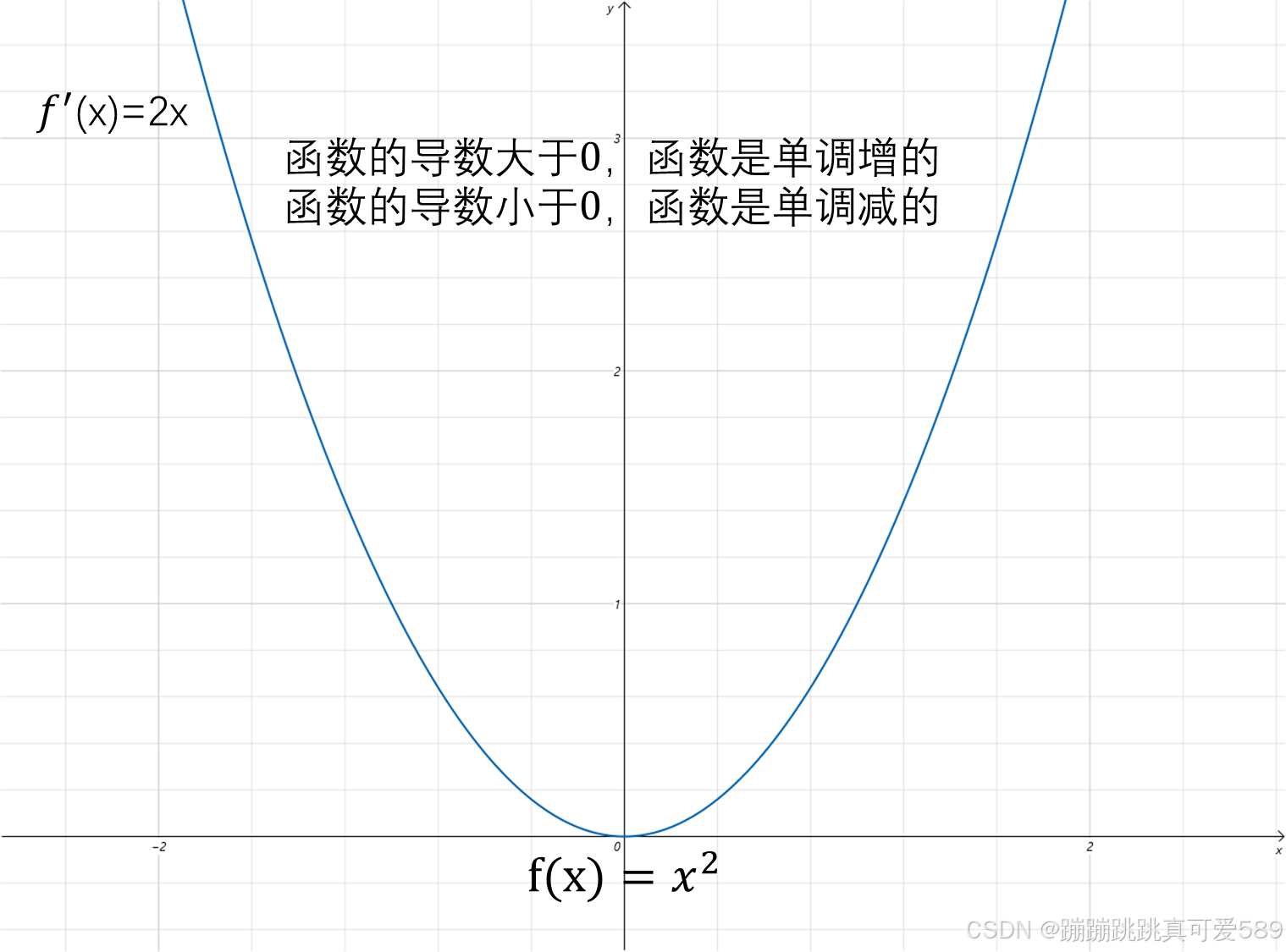
通过判断函数的导数在某个区间是否大于0,就可以判断原函数的单调性
- 函数的导数大于0,原函数是单调增的
- 函数的导数小于0,原函数是单调减的
六、函数的极值
6.1、极值
若函数f(x)在x₀的一个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x₀),则称f(x₀)
是函数f(x)的一个极大值,点x₀称为极大值点;同理,若有f(x)>f(x₀),则称f(x₀)是函数f(x)的
一个极小值,点x₀称为极小值点。
- 极大值和极小值统称为函数的极值
- 极大值点和极小值点统称为函数的极值点
注意
函数的极值是一个局部概念,它只是在极值点附近的所有点的函数值相比较而言的!
6.2、极值定理
设函数f(x)在点x₀处具有导数,且x₀是极值点,则函数在点x₀处的导数必为零,即f'(x₀)=0.
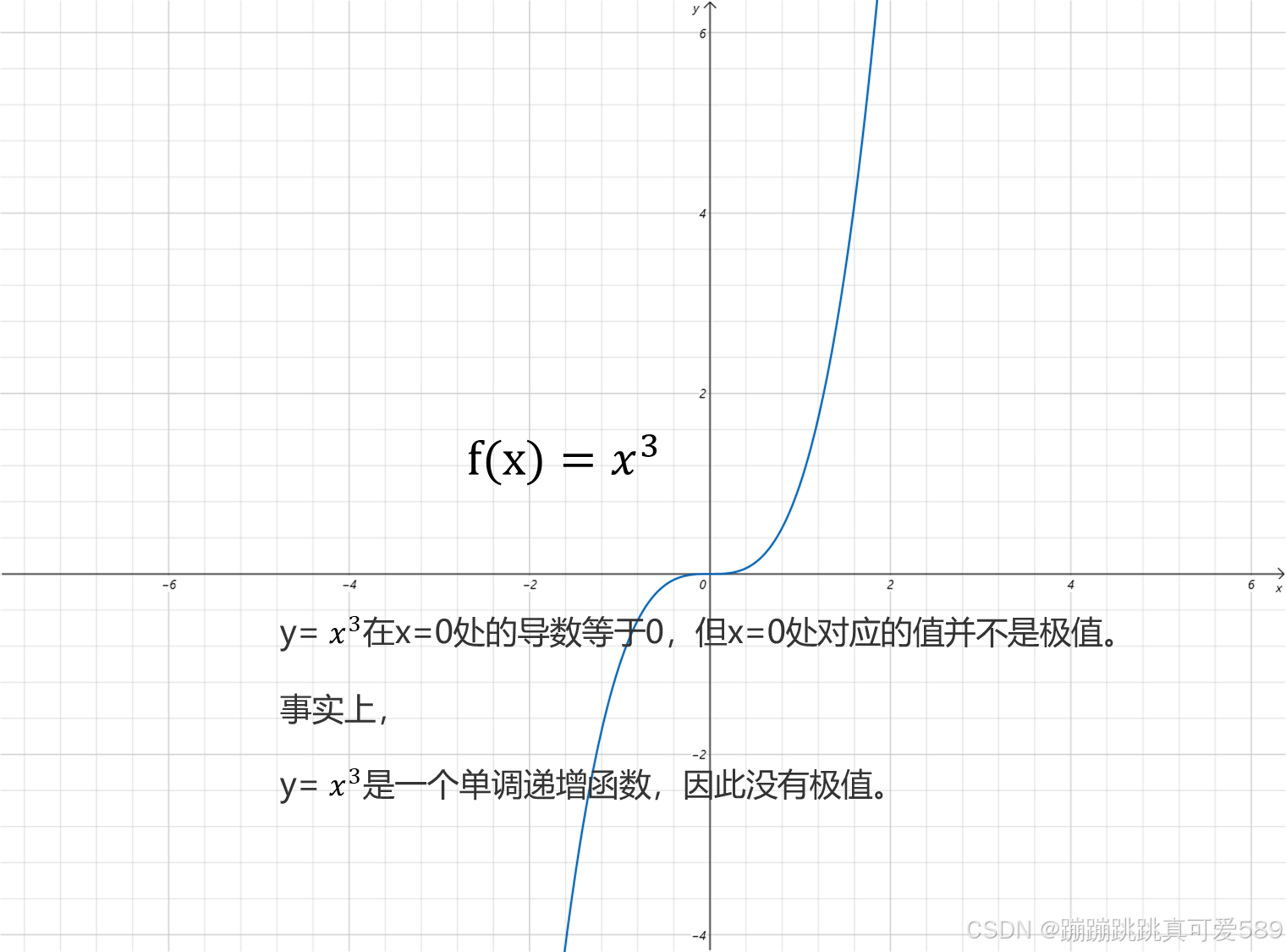
注意
导数等于0处不一定是极值!
七、二阶导数判断凹凸性_泰勒展开式
7.1、函数的凹凸性
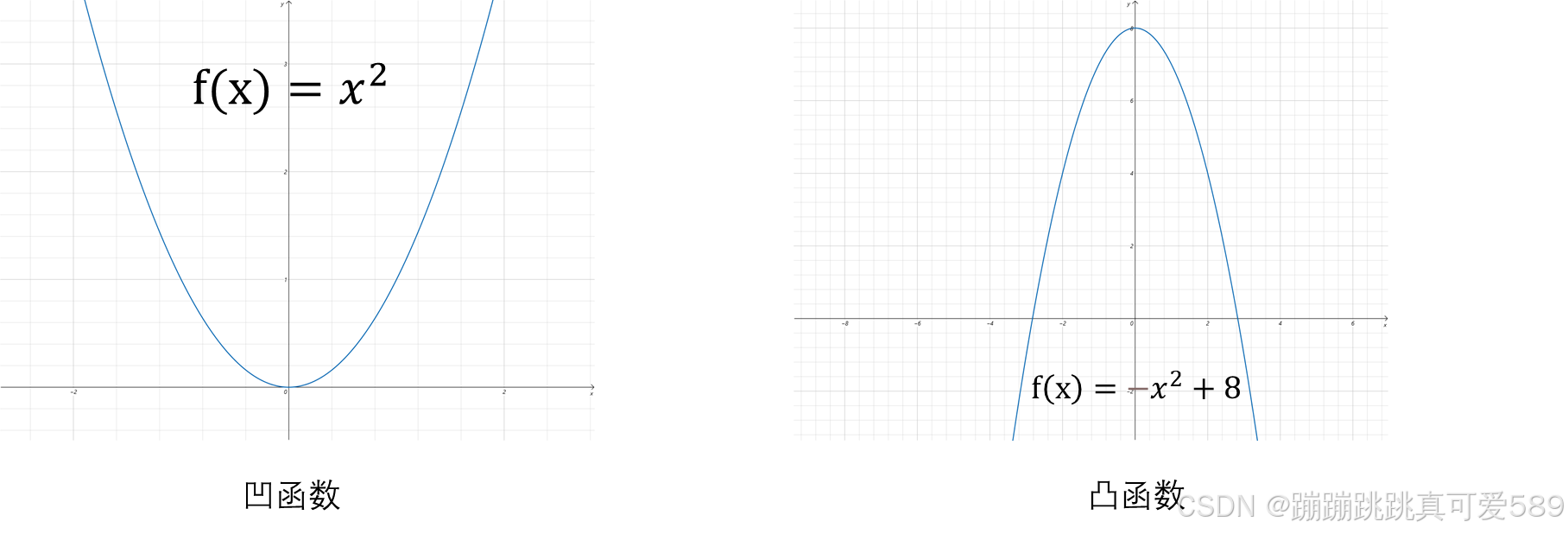
为了研究函数曲线的弯曲方向,引入了“凹凸性”的概念
- 如果连接曲线上任意两点的割线段都在该两点间的曲线弧之上,那么该段曲线弧称为凹的,反之则为凸的。
- 设f(x)在[a,b]上连续,在(a,b)内具有二阶导数
若函数f(x)在(a,b)内有f'(x)>0,则函数曲线在[a,b]上是凹的;
若函数f(x)在(a,b)内有f'(x)<0,则函数曲线在[a,b]上是凸的;
7.2、泰勒公式
泰勒公式它将一些复杂的函数近似地表示为简单的多项式函数,泰勒公式这种化繁为简的功能,使得它成为分析和研究许多数学问题的有力工具。
- 泰勒展开是通过多项式函数来近似一个可导函数 f(x),在 x=x~0~ 处进行泰勒展开
- 很多时候函数 f(x)可能会非常复杂,这时可以使用泰勒展开做一个近似
- 一元函数泰勒展开
八、不可微函数
如果一个点存在导数,那么该点的函数会被该点微分。也就是说:如果要使函数在整个区间内保持微分,则该区间中的每个点都必须存在寻数。
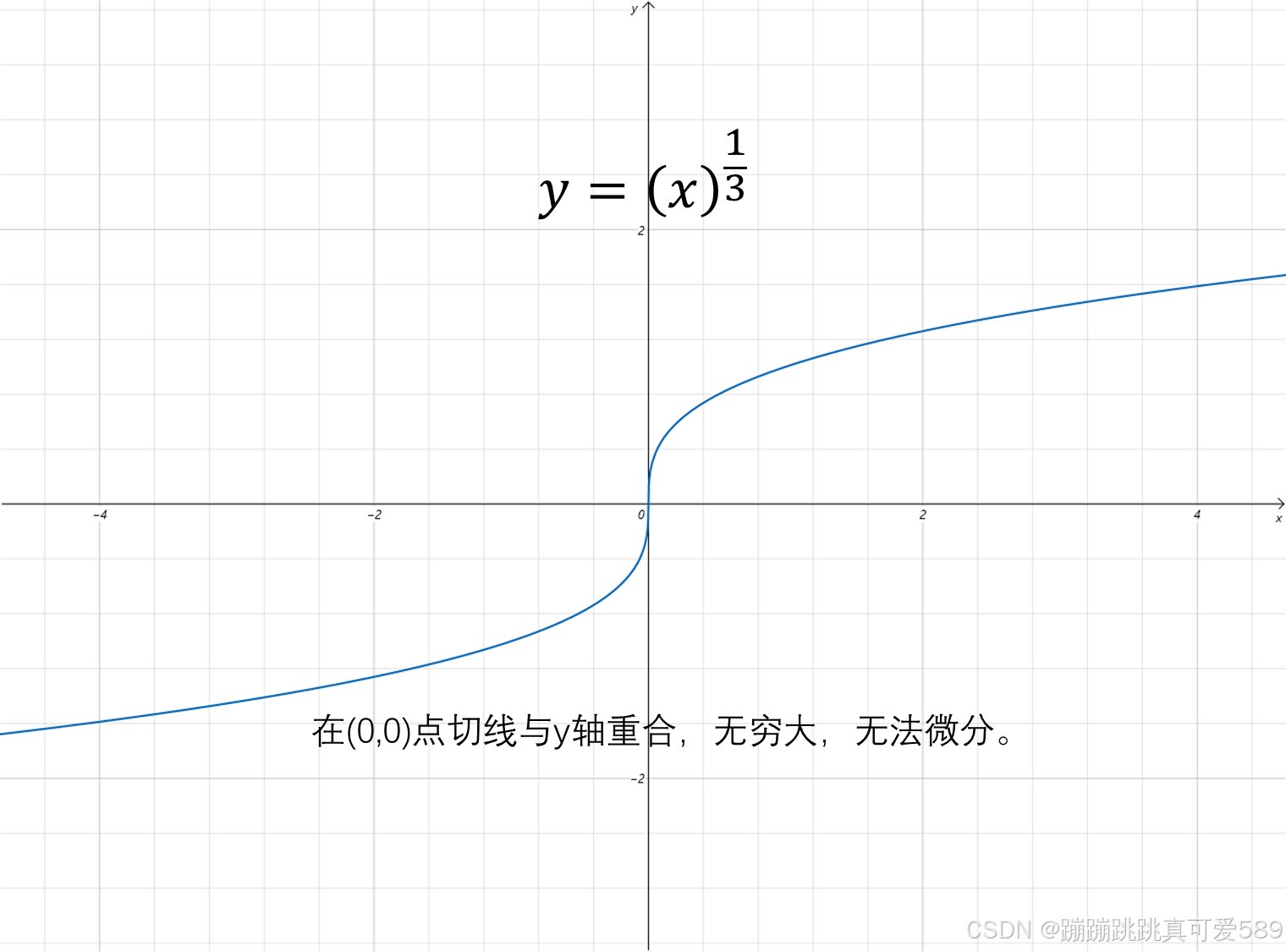
实际上,并不是所有的函数在每个点都可以找到导数,这些函数称为:不可微函数。
如果一个点存在导数,那么该点的函数会被该点微分。也就是说:如果要使函数在整个区间内保持微分,则该区间中的每个点都必须存在寻数。
实际上,并不是所有的函数在每个点都可以找到导数,这些函数称为:不可微函数。