Bootstrap

C语言大作业 ----- 整数处理程序

目录

前言

大家好哇，本人是大一的一名学生。刚学了一学期的C语言，发现挺有兴趣的hhhhhh.就在假期买了一本基础入门的书《C Primer Plus》来学习了一番。买的时候也没管太多，不管书的评价好坏与否(个人觉得还是很不错滴)，反正也快看完了。又恰逢老师留了几个新手拿来练手的大作业，就想检验一下自己学的成果，也想通过写文章来获取大家的建议。有点啰嗦了…开始吧！

题目要求

第一题是要求我们写出一个整数处理程序。
输入两个正整数 m 和 n, 要求完成以下任务：

  1. 求出 m 和 n 两数之间所有明7暗7数。
  2. 分别求出 m! 和 n!。
  3. 求 m 和 n 的最大公约数和最小公倍数。
  4. 求出 m 和 n 之间的所有回文数。
  5. 求出 m 和 n 之间的所有素数。
  6. 求出 m 和 n 之间的所有完数。

老师还说每个任务至少编写一个函数来完成，而且函数越多越好。
(文章最后附完整源代码)

整体思路

这道题目涉及的内容都是些较基础的，所以开干就完了，要啥功能写啥函数。(我也并没有设置输入判断，假设用户输入的都是正整数)
首先， 既然要处理两个整数，那之后调用的函数都要用到 m 和 n。我们假设函数要处理的对象都是后者>=前者,那么如果用户输入的 m < n, 就调换 m 和 n 的值。我们来编写一个交换两数数值的函数。

  • 传指针
void swap(int * pa, int *pb)
{
	/* 
	** 函数功能：交换两个数 
	** 参    数：*pa, *pb 要交换两数的地址 
	** 返 回 值：无 
	*/
	int temp;   // 中间值 

	temp = *pa;
	*pa = *pb;
	*pb = temp;
}

再用#define预处理指令设置一行要打印的数字数量

#define K 8      // 一行内打印数字的次数

“明7暗7数”

  • 明7：就是数字里包含‘7’这个数的，如37,173等等。
  • 暗7：就是能被7整除的数，如49,63等对7求模得0的数(0除外)。
  • 代码如下
void seven(int m, int n)
{
	/* 
	** 函数功能：输出两数之间所有"明7暗7"数 
	** 参    数：m, n 待处理对象 
	** 返 回 值：无 
	*/
	int i, count = 0;  // count 已打印数量 

	printf("\n%d与%d之间的\"明7暗7\"数有：\n", m, n);
	printf("包含7的数有：\n");
	for (i = m; i <= n; i++)
	{
		if (within_seven(i))   // 判断是否包含"7" 
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行 
				printf("\n");
		}
	}
	count = 0;
	printf("\n能被7整除的数有：\n");
	for (i = m; i <= n; i++)
	{
		if (i % 7 == 0)  // 判断是否被7整除 
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}
	}
	printf("\n");
}
  • 上面的代码块中有一个within_seven()函数,是用来判断“明7数”的。
int within_seven(int n)
{
	/* 
	** 函数功能：判断是否包含"7" 
	** 参    数：n 待处理对象 
	** 返 回 值：[1为包含，0为不包含] 
	*/
	char number[10];

	sprintf(number, "%d", n);  // 把整数参数存为字符串处理 
	if (strchr(number, '7'))
		return 1;

	return 0;
}
  • 用到了字符串函数strchr()所以程序要包含<string.h>头文件。
  • 还有利用输入流sprintf()函数把数字转换为字符串以便处理。

求阶乘

  • 这个函数直接返回参数的阶乘好了。 代码如下
double factorial(int n)
{
	/* 
	** 函数功能：计算阶乘 
	** 参    数：n 待处理对象 
	** 返 回 值：n 的阶乘 
	*/
	double fac = 1;

	for (int i = 1; i <= n; i++)
	{
		fac *= i;
	}

	return fac;
}
  • 我这里用了循环，还可以用递归。
double factorial(int n)
{
	if (n == 0)
		return 1;
	else
		return n * factorial(n - 1);
}
  • 主函数内调用情况
	printf("\n输入两数的阶乘：");
	printf("\n%3d! = ", m);          // 阶乘小用%lf打印，太大用%e打印
	printf((m > 15)? "%.13e\n" : "%.0lf\n", factorial(m));
	printf("%3d! = ", n);
	printf((n > 15)? "%.13e\n" : "%.0lf\n", factorial(n));
  • 可能注意到了我这里很麻烦，浮点数可以直接用%g打印

最大公约数及最小公倍数

  • 结果也直接返回到主程序。
  • 这里用了枚举法(别的方法我竟然还没有尝试过)。代码如下
int gys(int m, int n)
{
	/*
	** 函数功能：计算两数最大公约数
	** 参    数：m, n 待处理对象
	** 返 回 值：最大公约数
	*/
	int i, max;

	for (i = 1; i <= m; i++)
	{
		if (m % i == 0 && n % i == 0)
			max = i;                      // 循环赋给max最大公约数
	}

	return max;
}

int gbs(int m, int n)
{
	/*
	** 函数功能：计算两数最小公倍数
	** 参    数：m, n 待处理对象
	** 返 回 值：最小公倍数
	*/
	return (m * n / gys(m, n));  // 两个数的积 = 最小公倍数 * 最大公约数
}

回文数

  • 接下来就是求回文数(正着读反着读都一样的数)。也转换成字符串处理。
  • 代码如下
void palindrome(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有回文数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, count = 0;  // count 已打印数量

	printf("\n%d与%d之间的回文数有：\n", m, n);
	for (i = m; i <= n; i++)
	{
		if (is_palin(i))  // 判断是否为回文数
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}

	}
	printf("\n");
}

int is_palin(int n)
{
	/*
	** 函数功能：判断是否为回文数
	** 参    数：n 待处理对象
	** 返 回 值：[1为回文，0不是]
	*/
	int i, len, count = 0;       // len 参数长度
	char number[10], rever[10];

	sprintf(number, "%d", n);  // 把参数存为字符串
	len = strlen(number);
	reverse(number, rever);    // 倒序存在另一字符串

	for (i = 0; i < len; i++)
	{
		if (number[i] == rever[i])   // 如对应字符相同，count+1
			count++;
	}

	if (count == len)           // 相同字符数等同原字符串长度，返回1
		return 1;

	return 0;
}
  • 上面也包含着一个判断是否为回文数的函数。
  • 下面给出倒置字符串函数(可能因为我处理得不够好，这部分代码感觉很繁琐)
void reverse(char * source, char * target)
{
	/*
	** 函数功能：倒置另存字符串
	** 参    数：原字符数组，目标字符数组
	** 返 回 值：无
	*/
	int i, j, srclen = strlen(source);

	for (i = srclen - 1, j = 0; i >= 0; i--, j++)
	{
		*(target + j) = *(source + i);
	}
}
  • 处理回文数函数和剩下的两个函数都很相似，都包含着一个判断的函数作为 if 的判断条件。

素数

  • 直接上代码
void prime(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有素数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, count = 0;  // count 已打印数量

	printf("\n%d与%d之间的素数有：\n", m, n);
	for (i = m; i <= n; i++)
	{
		if (is_prime(i))  // 判断是否为素数
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}
	}
	printf("\n");
}

int is_prime(int n)
{
	/*
	** 函数功能：判断是否为素数
	** 参    数：n 待处理对象
	** 返 回 值：[1为素数，0不是]
	*/
	int i = 2;

	if (n == 1)
		return 0;  // 1不是素数
	if (n == 2)
		return 1;  // 2是素数
	for (i = 2; i < n ; i++)
	{
		if (n % i == 0)
			return 0;
	}

	return 1;
}

完数

  • 废话少说
  • (还是说一下，完数:一个数的所有因子(包括1)之和等于它自身。)
void perfect(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有完数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, j;

	printf("\n%d与%d之间的所有完数及其因子：\n", m, n);
	for (i = m; i <= n; i++)
	{
		if (is_perfect(i))  // 判断是否为完数
		{
			printf("%5d 的因子有 ", i);
			for (j = 1; j < i; j++)
			{
				if (i % j == 0)
					printf("%d,", j);
			}
			printf("\b \n");
		}
	}
	printf("\n");
}

int  is_perfect(int n)
{
	/*
	** 函数功能：判断是否为完数
	** 参    数：n 待处理对象
	** 返 回 值：[1是完数，0不是]
	*/
	int i, sum = 0;

	for (i = 1; i < n; i++)
	{
		if (n % i == 0)
			sum += i;
	}
	if (sum == n)
		return 1;

	return 0;
}
  • 品吧。

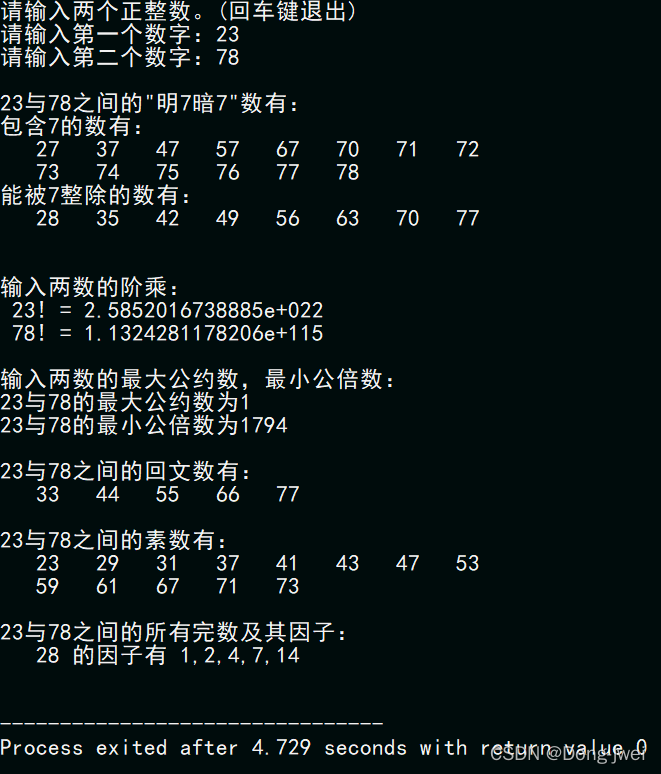
运行截图

在这里插入图片描述

结束语

函数的数量老师应该会满意吧~
我发布的第一篇文章就到这里啦。程序有很多的不足，日后也会改进，也希望各位可以给出宝贵的意见！后续还有5个题吧我记着…做完也会慢慢发布的。敬请期待。。。
差点忘了完整源码

#include <stdio.h>
#include <string.h>

#define K 8      // 一行内打印数字的次数 
#define _ 0

// 函数原型
void swap         (int *, int *);    // 交换两数
void seven        (int, int);        // 输出"明7暗7"数
int  within_seven (int);             // 判断是否包含"7"
double factorial  (int);             // 阶乘
int  gys          (int, int);        // 最大公约数
int  gbs          (int, int);        // 最小公倍数
void palindrome   (int, int);        // 输出回文数
int  is_palin     (int);             // 判断回文数
void prime        (int, int);        // 输出素数
int  is_prime     (int);             // 判断素数
void perfect      (int, int);        // 输出完数
int  is_perfect   (int);             // 判断完数
void reverse      (char *, char *);  // 倒置字符串

int main()
{
	int m, n;

	printf("请输入两个正整数。(回车键退出)\n");
	printf("请输入第一个数字：");
	scanf("%d", &m);
	printf("请输入第二个数字：");
	scanf("%d", &n);

	if (m > n)              // 如果m > n, 交换
		swap(&m, &n);

	seven(m, n);  // 输出"明7暗7"数

	printf("\n输入两数的阶乘：");
	printf("\n%3d! = ", m);          // 阶乘小用%lf打印，太大用%e打印
	printf((m > 15)? "%.13e\n" : "%.0lf\n", factorial(m));
	printf("%3d! = ", n);
	printf((n > 15)? "%.13e\n" : "%.0lf\n", factorial(n));

	printf("\n输入两数的最大公约数，最小公倍数：\n");
	printf("%d与%d的最大公约数为%d\n", m, n, gys(m, n));
	printf("%d与%d的最小公倍数为%d\n", m, n, gbs(m, n));

	palindrome(m, n);  // 输出回文数

	prime(m, n);       // 输出素数

	perfect(m, n);     // 输出完数

	return (0^_^0);
}

void swap(int * pa, int *pb)
{
	/*
	** 函数功能：交换两个数
	** 参    数：*pa, *pb 要交换两数的地址
	** 返 回 值：无
	*/
	int temp;   // 中间值

	temp = *pa;
	*pa = *pb;
	*pb = temp;
}

void seven(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有"明7暗7"数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, count = 0;  // count 已打印数量

	printf("\n%d与%d之间的\"明7暗7\"数有：\n", m, n);
	printf("包含7的数有：\n");
	for (i = m; i <= n; i++)
	{
		if (within_seven(i))   // 判断是否包含"7"
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}
	}
	count = 0;
	printf("\n能被7整除的数有：\n");
	for (i = m; i <= n; i++)
	{
		if (i % 7 == 0)  // 判断是否被7整除
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}
	}
	printf("\n");
}

int within_seven(int n)
{
	/*
	** 函数功能：判断是否包含"7"
	** 参    数：n 待处理对象
	** 返 回 值：[1为包含，0为不包含]
	*/
	char number[10];

	sprintf(number, "%d", n);  // 把整数参数存为字符串处理
	if (strchr(number, '7'))
		return 1;

	return 0;
}

double factorial(int n)
{
	/*
	** 函数功能：计算阶乘
	** 参    数：n 待处理对象
	** 返 回 值：n 的阶乘
	*/
	double fac = 1;

	for (int i = 1; i <= n; i++)
	{
		fac *= i;
	}

	return fac;
}

int gys(int m, int n)
{
	/*
	** 函数功能：计算两数最大公约数
	** 参    数：m, n 待处理对象
	** 返 回 值：最大公约数
	*/
	int i, max;

	for (i = 1; i <= m; i++)
	{
		if (m % i == 0 && n % i == 0)
			max = i;                      // 循环赋给max最大公约数
	}

	return max;
}

int gbs(int m, int n)
{
	/*
	** 函数功能：计算两数最小公倍数
	** 参    数：m, n 待处理对象
	** 返 回 值：最小公倍数
	*/
	return (m * n / gys(m, n));  // 两个数的积 = 最小公倍数 * 最大公约数
}

void palindrome(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有回文数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, count = 0;  // count 已打印数量

	printf("\n%d与%d之间的回文数有：\n", m, n);
	for (i = m; i <= n; i++)
	{
		if (is_palin(i))  // 判断是否为回文数
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}

	}
	printf("\n");
}

int is_palin(int n)
{
	/*
	** 函数功能：判断是否为回文数
	** 参    数：n 待处理对象
	** 返 回 值：[1为回文，0不是]
	*/
	int i, len, count = 0;       // len 参数长度
	char number[10], rever[10];

	sprintf(number, "%d", n);  // 把参数存为字符串
	len = strlen(number);
	reverse(number, rever);    // 倒序存在另一字符串

	for (i = 0; i < len; i++)
	{
		if (number[i] == rever[i])   // 如对应字符相同，count+1
			count++;
	}

	if (count == len)           // 相同字符数等同原字符串长度，返回1
		return 1;

	return 0;
}

void reverse(char * source, char * target)
{
	/*
	** 函数功能：倒置另存字符串
	** 参    数：原字符数组，目标字符数组
	** 返 回 值：无
	*/
	int i, j, srclen = strlen(source);

	for (i = srclen - 1, j = 0; i >= 0; i--, j++)
	{
		*(target + j) = *(source + i);
	}
}

void prime(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有素数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, count = 0;  // count 已打印数量

	printf("\n%d与%d之间的素数有：\n", m, n);
	for (i = m; i <= n; i++)
	{
		if (is_prime(i))  // 判断是否为素数
		{
			printf("%5d", i);
			count++;
			if (count % K == 0)  // 每打印K个数字换行
				printf("\n");
		}
	}
	printf("\n");
}

int is_prime(int n)
{
	/*
	** 函数功能：判断是否为素数
	** 参    数：n 待处理对象
	** 返 回 值：[1为素数，0不是]
	*/
	int i = 2;

	if (n == 1)
		return 0;  // 1不是素数
	if (n == 2)
		return 1;  // 2是素数
	for (i = 2; i < n ; i++)
	{
		if (n % i == 0)
			return 0;
	}

	return 1;
}

void perfect(int m, int n)
{
	/*
	** 函数功能：输出两数之间所有完数
	** 参    数：m, n 待处理对象
	** 返 回 值：无
	*/
	int i, j;

	printf("\n%d与%d之间的所有完数及其因子：\n", m, n);
	for (i = m; i <= n; i++)
	{
		if (is_perfect(i))  // 判断是否为完数
		{
			printf("%5d 的因子有 ", i);
			for (j = 1; j < i; j++)
			{
				if (i % j == 0)
					printf("%d,", j);
			}
			printf("\b \n");
		}
	}
	printf("\n");
}

int  is_perfect(int n)
{
	/*
	** 函数功能：判断是否为完数
	** 参    数：n 待处理对象
	** 返 回 值：[1是完数，0不是]
	*/
	int i, sum = 0;

	for (i = 1; i < n; i++)
	{
		if (n % i == 0)
			sum += i;
	}
	if (sum == n)
		return 1;

	return 0;
}

再见！

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
诺禾：诺禾自述月薪2W的Java开发工程师，需要掌握哪些技能点？
C2W3.LAB.N-grams+Language Model+OOV
Python操作Excel
毕业论文格式大全、排版技巧及常见问题汇总
数据结构之链表操作详解与示例（反转链表，合并链表，旋转链表，对链表排序）
ROS 学习踩坑笔记4-在moveit编译时找不到manipulation_msgsConfig.cmake manipulation_msgs-config.cmake文件
InnoDB对MVCC的实现
Emo伤感竖屏视频素材哪里找？令人伤感的素材库分享
RabbitMQ在springboot项目中的应用（实际项目，测试可用）
蓝牙通信UUID
;