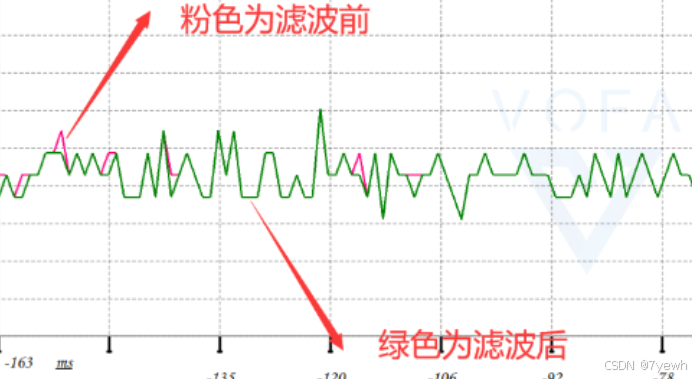
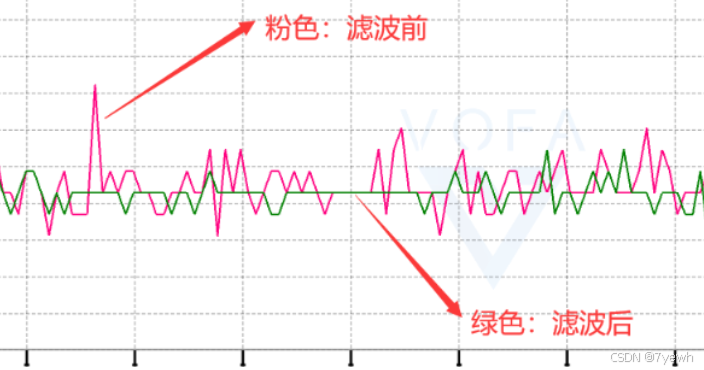
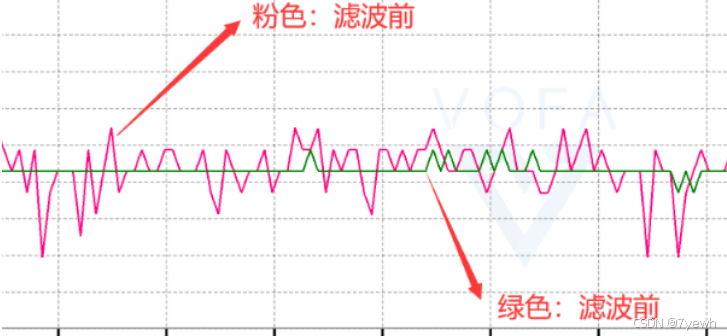
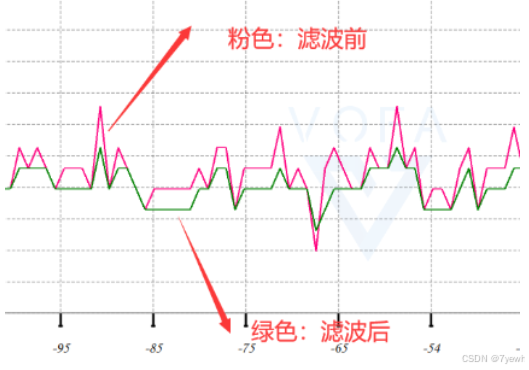
例如,STM32进行滤波处理时,主要目的是处理数据采集过程中可能产生的噪声和尖刺信号。这些噪声可能来自电源干扰、传感器自身的不稳定性或其他外部因素。
1.一阶互补滤波
方法:取a=0~1,本次滤波结果=(1-a)本次采样值+a上次滤波结果 优点:对周期性干扰具有良好的抑制作用适用于波动频率较高的场合 缺点:相位滞后,灵敏度低滞后程度取决于a值大小不能消除滤波频率高于采样频率的1/2的干扰信号。
int firstOrderFilter(int newValue, int oldValue, float a)
{
return a * newValue + (1-a) * oldValue;
}2.中位值滤波
方法:连续采样N次(N取奇数)把N次采样值按大小排列取中间值为本次有效值 优点:能有效克服因偶然因素引起的波动干扰;对温度、液位等变化缓慢的被测参数有良好的滤波效果 缺点:对流量,速度等快速变化的参数不宜。
//中值滤波算法
int middleValueFilter(int N)
{
int value_buf[N];
int i,j,k,temp;
for( i = 0; i < N; ++i)
{
value_buf[i] = HAL_ADC_GetValue(&hadc1);
}
for(j = 0 ; j < N-1; ++j)
{
for(k = 0; k < N-j-1; ++k)
{
//从小到大排序,冒泡法排序
if(value_buf[k] > value_buf[k+1])
{
temp = value_buf[k];
value_buf[k] = value_buf[k+1];
value_buf[k+1] = temp;
}
}
}
return value_buf[(N-1)/2];
}3.算术平均滤波
方法:连续取N个采样值进行算术平均运算; N值较大时:信号平滑度较高,但灵敏度较低 N值较小时:信号平滑度较低,但灵敏度较高 N值的选取:一般流量,N=12;压力:N=4 优点:试用于对一般具有随机干扰的信号进行滤波。这种信号的特点是有一个平均值,信号在某一数值范围附近上下波动。 缺点:测量速度较慢或要求数据计算较快的实时控制不适用。
int averageFilter(int N)
{
int sum = 0;
short i;
for(i = 0; i < N; ++i)
{
sum += HAL_ADC_GetValue(&hadc1);
}
return sum/N;
}4.滑动平均滤波
方法:把连续取N个采样值看成一个队列,队列的长度固定为N。每次采样到一个新数据放入队尾,并扔掉原来队首的一次数据(先进先出原则)。把队列中的N个数据进行算术平均运算,就可获得新的滤波结果。 N值的选取:流量,N=12;压力:N=4;液面,N=4~12;温度,N=1~4 优点:对周期性干扰有良好的抑制作用,平滑度高;试用于高频振荡的系统 缺点:灵敏度低;对偶然出现的脉冲性干扰的抑制作用较差,不适于脉冲干扰较严重的场合 比较浪费RAM(改进方法,减去的不是队首的值,而是上一次得到的平均值)
//平滑均值滤波
#define N 10
int value_buf[N];
int sum=0;
int curNum=0;
int moveAverageFilter()
{
if(curNum < N)
{
value_buf[curNum] = HAL_ADC_GetValue(&hadc1);
sum += value_buf[curNum];
curNum++;
return sum/curNum;
}
else
{
sum -= sum/N;
sum += HAL_ADC_GetValue(&hadc1);
return sum/N;
}
}5.限幅平均滤波
方法:相当于“限幅滤波法”+“递推平均滤波法” 每次采样到的新数据先进行限幅处理再送入队列进行递推平均滤波处理 优点:对于偶然出现的脉冲性干扰,可消除有其引起的采样值偏差。 缺点:比较浪费RAM
//限幅平均滤波
#define A 50 //限制幅度阈值
#define M 12
int data[M];
int First_flag=0;
int LAverageFilter()
{
int i;
int temp,sum,flag=0;
data[0]=HAL_ADC_GetValue(&hadc1);
for(i=1;i<M;i++)
{
temp=HAL_ADC_GetValue(&hadc1);
if((temp-data[i-1])>A||((data[i-1]-temp)>A))
{
i--;flag++;
}
else
{
data[i]=temp;
}
}
for(i=0;i<M;i++)
{
sum+=data[i];
}
return sum/M;
}6.卡尔曼滤波
核心思想:根据当前的仪器"测量值" 和上一刻的 “预测量” 和 “误差”,计算得到当前的最优量,再预测下一刻的量。里面比较突出的是观点是:把误差纳入计算,而且分为预测误差和测量误差两种,通称为噪声。还有一个非常大的特点是:误差独立存在,始终不受测量数据的影响。
优点:巧妙的融合了观测数据与估计数据,对误差进行闭环管理,将误差限定在一定范围。适用性范围很广,时效性和效果都很优秀。
缺点:需要调参,参数的大小对滤波的效果影响较大。
//卡尔曼滤波
int KalmanFilter(int inData)
{
static float prevData = 0; //先前数值 上一次滤波后的数据,作为下一次滤波的初始值
static float p = 10, q = 0.001, r = 0.001, kGain = 0; // q控制误差 r控制响应速度
//更新估计误差方差
p = p + q;
//计算卡尔曼增益
kGain = p / ( p + r );
//计算本次滤波估计值
inData = prevData + ( kGain * ( inData - prevData ) );
//更新测量方差
p = ( 1 - kGain ) * p;
prevData = inData;
return inData; //返回滤波值
}prevData:保存上一次滤波后的数据,用于下一次的滤波。 p:估计误差方差,表示当前估计值的不确定性。 q:过程噪声方差,表示系统模型的不确定性。 r:测量噪声方差,表示测量数据的不确定性。 kGain:卡尔曼增益,决定了测量数据和估计数据对当前状态估计的影响程度。
初始化静态变量
更新估计误差方差
计算卡尔曼增益
更新估计值
更新估计误差方差
保存当前估计值
返回滤波后的值
7.限幅滤波
核心思想:根据经验判断,确定两次采样允许的最大偏差值(设为A),每次检测到新值时判断: 如果本次值与上次值之差<=A,则本次值有效,如果本次值与上次值之差>A,则本次值无效,放弃本次值,用上次值代替本次值。 优点:能克服偶然因素引起的脉冲干扰 缺点:无法抑制周期性的干扰,平滑度差
#define A 51
u16 Value1;
u16 filter1()
{
u16 NewValue;
Value1 = ftable[b-1];
NewValue = ftable[b];
b++;
a++;
if(a==255) a=0;
if(b==255) b=1;
if(((NewValue - Value1) > A) || ((Value1 - NewValue) > A))
{
print_host(ftable[a],NewValue);
return NewValue;
}
else
{
print_host(ftable[a],Value1);
return Value1;
}
}8.加权递推平均滤波
核心思想: 是对递推平均滤波法的改进,即不同时刻的数据加以不同的权;通常是,越接近现时刻的数据,权取得越大,给予新采样值的权系数越大,则灵敏度越高,但信号平滑度越低。 优点: 适用于有较大纯滞后时间常数的对象,和采样周期较短的系统。 缺点: 对于纯滞后时间常数较小、采样周期较长、变化缓慢的信号;不能迅速反应系统当前所受干扰的严重程度,滤波效果差。
#define FILTER8_N 12
int coe[FILTER8_N] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}; // 加权系数表
int sum_coe = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12; // 加权系数和
int filter_buf[FILTER8_N + 1];
int filter8()
{
int i;
int filter_sum = 0;
filter_buf[FILTER8_N] = ftable[a];
a++;
if(a==255) a=0;
for(i = 0; i < FILTER8_N; i++)
{
filter_buf[i] = filter_buf[i + 1]; // 所有数据左移,低位仍掉
filter_sum += filter_buf[i] * coe[i];
}
filter_sum /= sum_coe;
// printf("%d\n",filter_sum);
return filter_sum;
}
void pros8(void)
{
u16 i=0;
for(i=0;i<255;i++)
{
print_host(ftable[i],filter8());
}
}9.消抖滤波
方法: 设置一个滤波计数器,将每次采样值与当前有效值比较: 如果采样值=当前有效值,则计数器清零; 如果采样值<>当前有效值,则计数器+1,并判断计数器是否>=上限N(溢出); 如果计数器溢出,则将本次值替换当前有效值,并清计数器。 优点: 对于变化缓慢的被测参数有较好的滤波效果; 可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动。 缺点: 对于快速变化的参数不宜; 如果在计数器溢出的那一次采样到的值恰好是干扰值,则会将干扰值当作有效值导入系统。
#define FILTER9_N 51
u16 i = 0;
u16 Value;
u16 filter9()
{
int new_value;
Value = ftable[b-1];
new_value = ftable[b];
b++;
if(b==255) b=1;
if(Value != new_value)
{
i++;
if(i > FILTER9_N)
{
i = 0;
Value = new_value;
}
}
else i = 0;
return Value;
}
void pros9(void)
{
u16 i=0;
for(i=0;i<255;i++)
{
print_host(ftable[i],filter9());
}
}