- 课程分为四大章节
一、级联频率响应
设计遇到的问题:
- 级联优化问题的复杂性:在设计放大器时,使用微波理论(例如伽马反射系数)会导致不同的反射系数绑定在一起,使得优化过程复杂并且不易解耦。
- 微波网络的复杂性:在微波设计中,伽马参数并不适用复杂的网络模型,尤其是在宽带设计中,因此需要避免使用微波定义,转而采用其他更适合的电路模型。
- 端口阻抗的宽带频变问题:当设计宽带LNA时,端口的阻抗变化会导致计算上的困难,尤其是阻抗不固定时,可能会导致S参数的变化。
- 匹配网络自身的版图优化:即使使用了PCell设计(参数化单元设计),优化工作仍然非常重复和复杂,因此需要寻求更高效的优化方法。
解决方案:
- 解耦优化:通过改进设计方法来避免反射系数和阻抗的相互依赖,简化优化过程。
- 使用新的电路模型:避免使用微波中的伽马定义,直接采用更加合适的电路模型进行设计。
- 动态阻抗匹配:在设计中引入动态阻抗匹配方法,避免使用固定阻抗,以解决宽带频变问题。
- 优化方法改进:通过引入预训练约束等技术来优化匹配网络的版图设计,减少重复劳动。
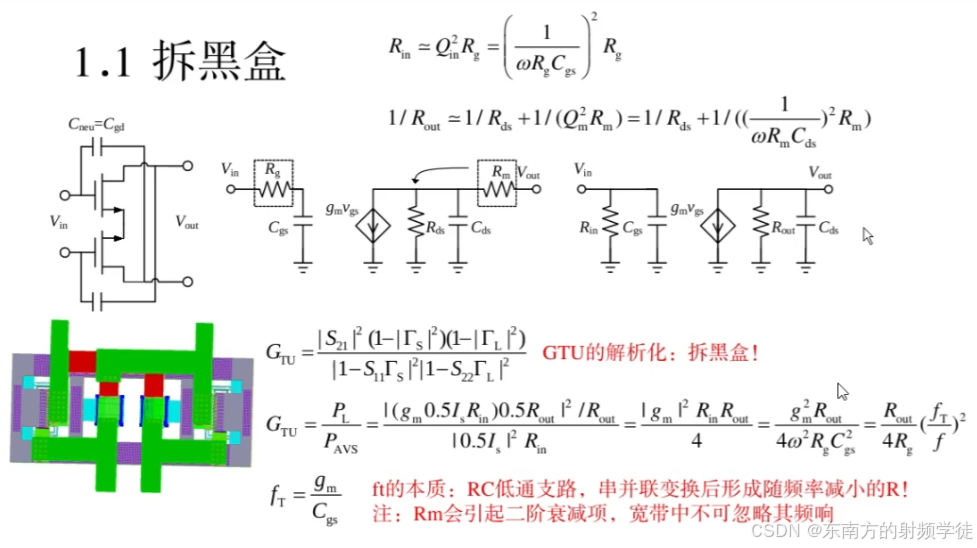
1.1 拆黑盒
1. 拆黑盒过程
- 黑盒模型:在传统设计中,放大器常被视作一个“黑盒”,我们通过输入S参数或Z参数来描述其行为。这些参数提供了放大器的性能信息,但它们并没有揭示内部的详细电路结构。为了在毫米波设计中取得更精确的结果,我们需要“拆解”这个黑盒,逐步分析每一个电路元件的行为。
2. 输入端与输出端的建模
-
输入端建模:
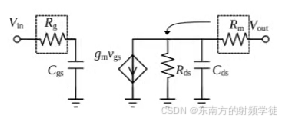
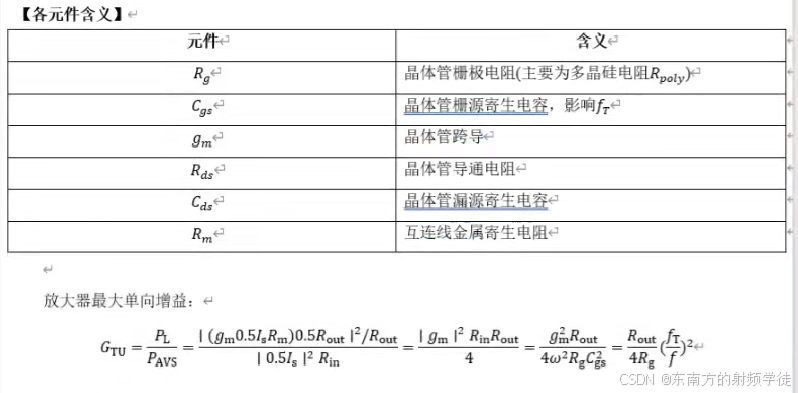
- 输入端通常由RG(输入电阻)和CGS(栅源电容)组成。公式中提到,输入端的阻抗 R i n R_{in} Rin可以通过频率和寄生参数来表示,特别是在频率较高时, R i n R_{in} Rin 会随着频率的增加而变化。
- 公式中有表达式:
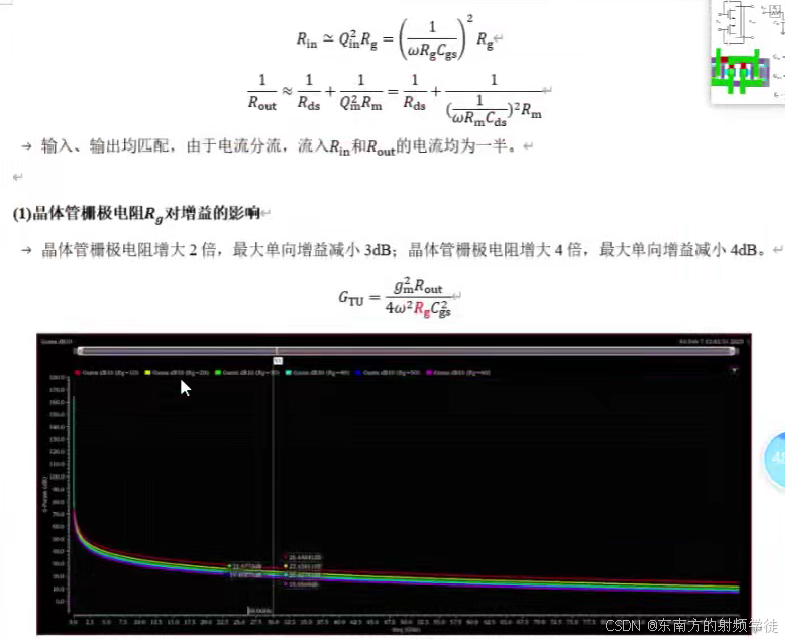
R i n = Q i n 2 R g = ( 1 ω R g C g s ) 2 R g R_\mathrm{in}=Q_\mathrm{in}^2R_\mathrm{g}=\left(\frac{1}{\omega R_\mathrm{g}C_\mathrm{gs}}\right)^2R_\mathrm{g} Rin=Qin2Rg=(ωRgCgs1)2Rg
这表明,输入阻抗随着频率的增加而减小。通过调整RG和CGS的参数,我们可以控制输入端的阻抗变化。
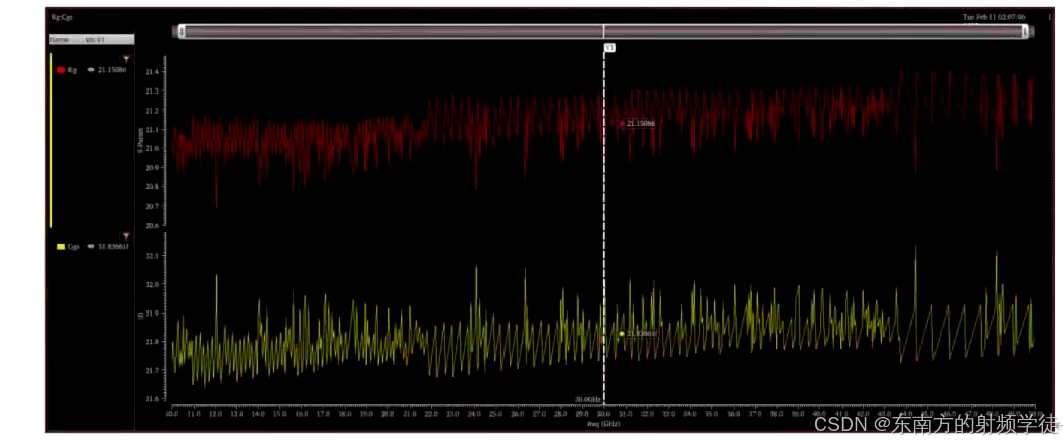
当串联转成并联的时候,会出现平方弱减项, - Rg和Cgs在0-50G是比较准的,随着频率变化,沿着等电阻圆移动
- Rg中r poly层电阻占大部分,其他的金属层根本就占不了多大的阻值
-
输出端建模:
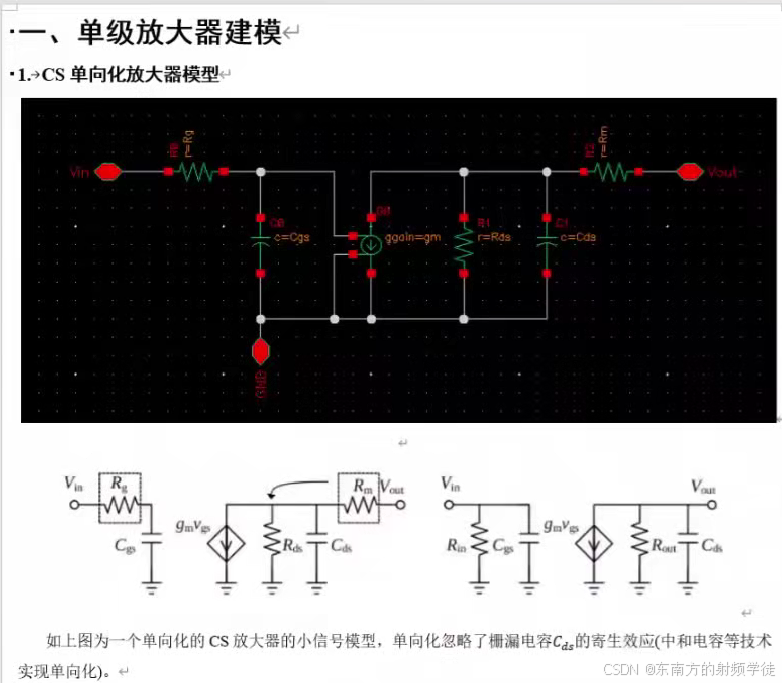
- 输出端涉及到RDS(漏极电阻)、CDS(漏源电容)以及RM(增益)等寄生元件。在毫米波设计中,输出端的建模更为复杂,需要三个元件来精确描述其特性,组成RC低通传递函数。通过调整这些元件,能够优化输出阻抗并提升增益。
1 / R o u t ≃ 1 / R d s + 1 / ( Q m 2 R m ) = 1 / R d s + 1 / ( ( 1 ω R m C d s ) 2 R m ) 1/R_{\mathrm{out}}\simeq1/R_{\mathrm{ds}}+1/(Q_{\mathrm{m}}^{2}R_{\mathrm{m}})=1/R_{\mathrm{ds}}+1/((\frac{1}{\omega R_{\mathrm{m}}C_{\mathrm{ds}}})^{2}R_{\mathrm{m}}) 1/Rout≃1/Rds+1/(Qm2Rm)=1/Rds+1/((ωRmCds1)2Rm) - 这里我们可以先加一个负电阻,使得S22扫描负电阻,让其出现在等电导圆上,抵消掉Rm,那么剩下的元件就是Rds和Cds并联形式。
- 输出端涉及到RDS(漏极电阻)、CDS(漏源电容)以及RM(增益)等寄生元件。在毫米波设计中,输出端的建模更为复杂,需要三个元件来精确描述其特性,组成RC低通传递函数。通过调整这些元件,能够优化输出阻抗并提升增益。
3. 增益分析与优化
-
增益公式:公式中提到增益GTU的计算方法:
G T U = ∣ S 21 ∣ 2 ( 1 − ∣ Γ s ∣ 2 ) ( 1 − ∣ Γ 1 ∣ 2 ) ∣ 1 − S 11 Γ S ∣ 2 ∣ 1 − S 22 Γ L ∣ 2 G_{\mathrm{TU}}=\frac{\mid S_{21}\mid^{2}(1-\mid\Gamma_{s}\mid^{2})(1-\mid\Gamma_{1}\mid^{2})}{\mid1-S_{11}\Gamma_{S}\mid^{2}\mid1-S_{22}\Gamma_{L}\mid^{2}} GTU=∣1−S11ΓS∣2∣1−S22ΓL∣2∣S21∣2(1−∣Γs∣2)(1−∣Γ1∣2)
其中, S 21 S_{21} S21是传输系数,表示从输入端到输出端的信号传输增益; Γ s \Gamma_s Γs和 Γ l \Gamma_l Γl分别是源端和负载端的反射系数。通过调整源端和负载端的反射系数,可以提高增益。- 在理想匹配情况下的增益表达式如下,将等效电路左右两侧加入并联LC谐振电路进行匹配。
G T U = P L P A V S = ∣ ( g m 0.5 I s R m ) 0.5 R o u t ∣ 2 / R o u t ∣ 0.5 I s ∣ 2 R i n G_{\mathrm{TU}}=\frac{P_{\mathrm{L}}}{P_{\mathrm{AVS}}}=\frac{|(g_{\mathrm{m}}0.5I_{\mathrm{s}}R_{\mathrm{m}})0.5R_{\mathrm{out}}|^{2}/R_{\mathrm{out}}}{|0.5I_{\mathrm{s}}|^{2}R_{\mathrm{in}}} GTU=PAVSPL=∣0.5Is∣2Rin∣(gm0.5IsRm)0.5Rout∣2/Rout
= ∣ g m ∣ 2 R m R o u t 4 = g m 2 R o u t 4 ω 2 R g C g s 2 = R o u t 4 R g ( f T f ) 2 =\frac{|g_{\mathrm{m}}|^{2}R_{\mathrm{m}}R_{\mathrm{out}}}{4}=\frac{g_{\mathrm{m}}^{2}R_{\mathrm{out}}}{4\omega^{2}R_{\mathrm{g}}C_{\mathrm{gs}}^{2}}=\frac{R_{\mathrm{out}}}{4R_{\mathrm{g}}}(\frac{f_{\mathrm{T}}}{f})^{2} =4∣gm∣2RmRout=4ω2RgCgs2gm2Rout=4RgRout(ffT)2 - 可以发现输入输出阻抗Rin和Rout越小,对应增益max gain越小,导致增益上不去的原因。这显示了通过增大输入和输出阻抗,可以提高输出功率,从而提升增益
- 在理想匹配情况下的增益表达式如下,将等效电路左右两侧加入并联LC谐振电路进行匹配。
-
频率衰减与增益关系:
- 由于随着频率的增加,输入和输出阻抗(例如RG和CGS)会发生变化,导致增益G_TU会随频率下降。理论上,增益的变化与频率的平方成正比:
G T U ∼ 1 f 2 G_{TU} \sim \frac{1}{f^2} GTU∼f21 - 这个公式表明,随着频率的提高,增益逐渐减小,通常是由于阻抗匹配不再理想。
- 由于随着频率的增加,输入和输出阻抗(例如RG和CGS)会发生变化,导致增益G_TU会随频率下降。理论上,增益的变化与频率的平方成正比:
4. FT(截止频率)
- FT的影响:FT是由电路的寄生效应引起的低通滤波器的结果。公式中给出的FT公式:
f T = g m C g s f_T = \frac{g_m}{C_{gs}} fT=Cgsgm
这里g_m是跨导(表示晶体管的增益能力),Cgs是栅源电容。FT的大小直接影响到放大器的性能,尤其是在高频(毫米波)情况下,FT越大,放大器的增益能力越强。
5. 设计优化
- 在设计宽带放大器时,特别是在毫米波频段,匹配网络的优化非常重要。通过合理的电阻、电感配置,可以提高输入和输出的匹配度,进而提高增益。
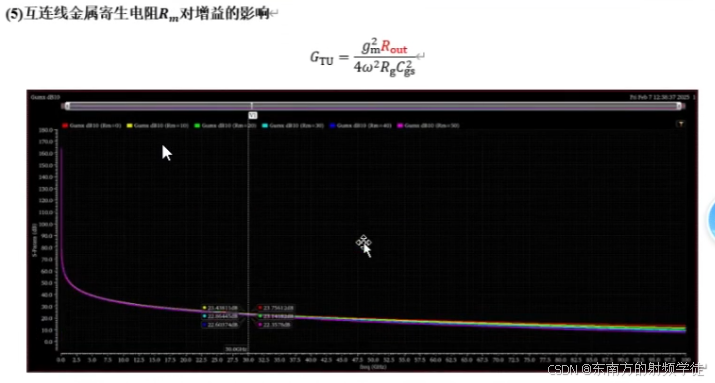
- 特别是,采用频变的电阻(如在高频情况下使用的频变电阻****Rm)来替代传统的固定阻抗设计,可以更好地适应宽频带的变化,从而避免了增益和频率不匹配的问题。
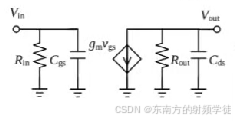
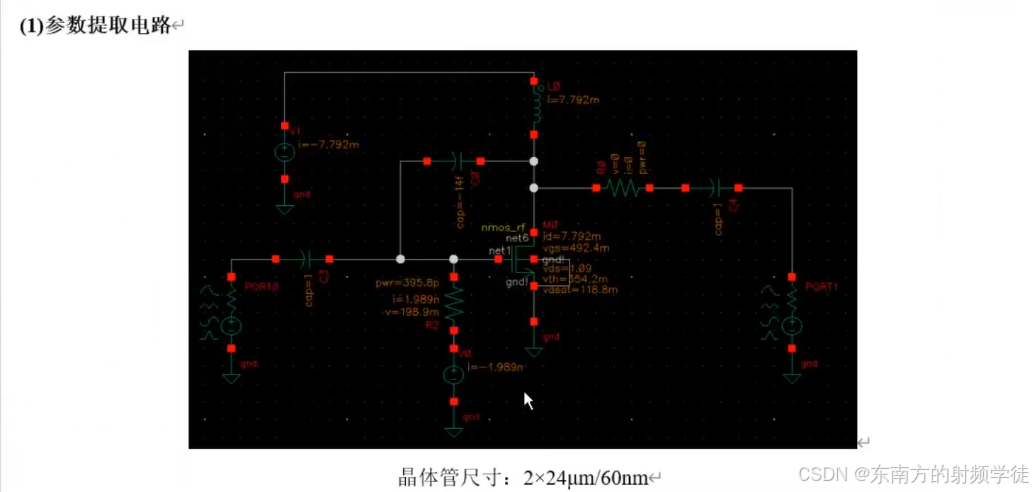
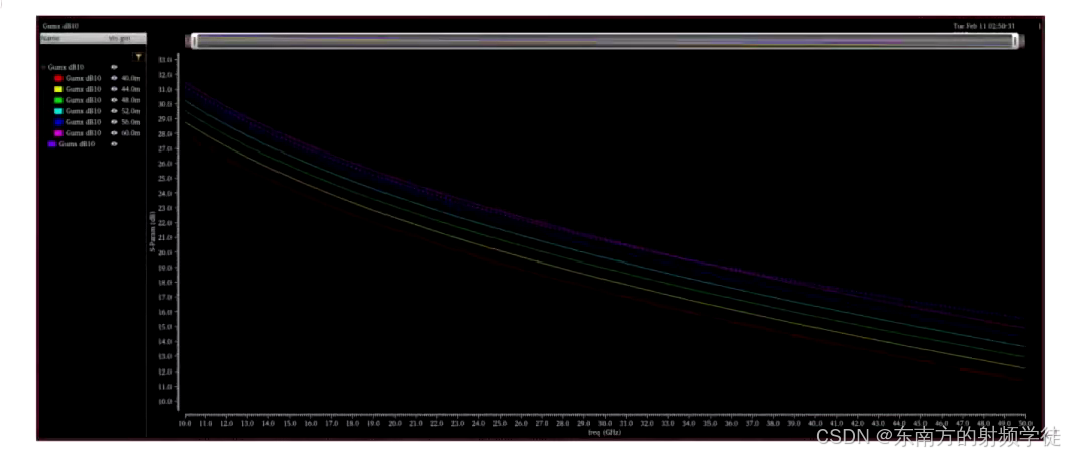
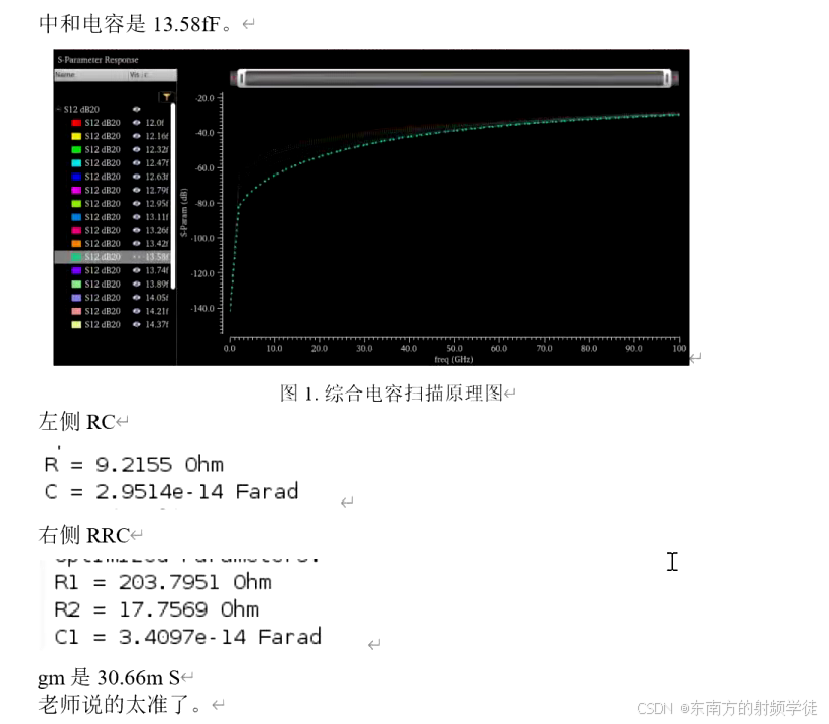
- 在实际设计中,我们先通常是先将原理图画完(图1带有中和电容的晶体管),中和电容使整个电路的S12达到最小。然后对整个电路(左下的电路layout)进行EMX电磁提取或者RC calibre提取,提取完之后当成是一个四端口的黑盒子(s4p文件)。然后对这个黑盒子进行仿真,提取得到右图的等效电路图。
1.2 S21到Z21的解耦合
- 可以发现贾海坤的论文中使用的是Z21作为放大器跨阻增益
- 使用Z21的出现的问题:第一,必须是MCR变压器才能使用,但是贾海坤的MCR的R是常数,随频率不会变化的,所以这里得到的平坦度公式是错的。第二点是,我们最后需要得到整个放大器增益是平坦的,而不是对于单个变压器MCR的增益是平坦的,这样得到的整个放大器增益带宽是非常窄的。
1. S参数与Z参数的关系
- S参数(散射参数)和Z参数(阻抗参数)是描述电路行为的两种常用方式。在设计放大器时,常常需要将S参数转换为Z参数,以便进行更精准的分析和优化。
- Z参数一般是集总模拟电路中使用到的东西
- 而这里我们使用到的是宏Z参数,其与Z参数的区别是,其将s参数的端口阻抗包含到黑盒子里面。
- 比如R0,其源阻抗和负载阻抗都等于50欧姆,这里将其画在了黑盒子里面。S参数的定义是包括了源和负载阻抗的,而Z参数不包含的。
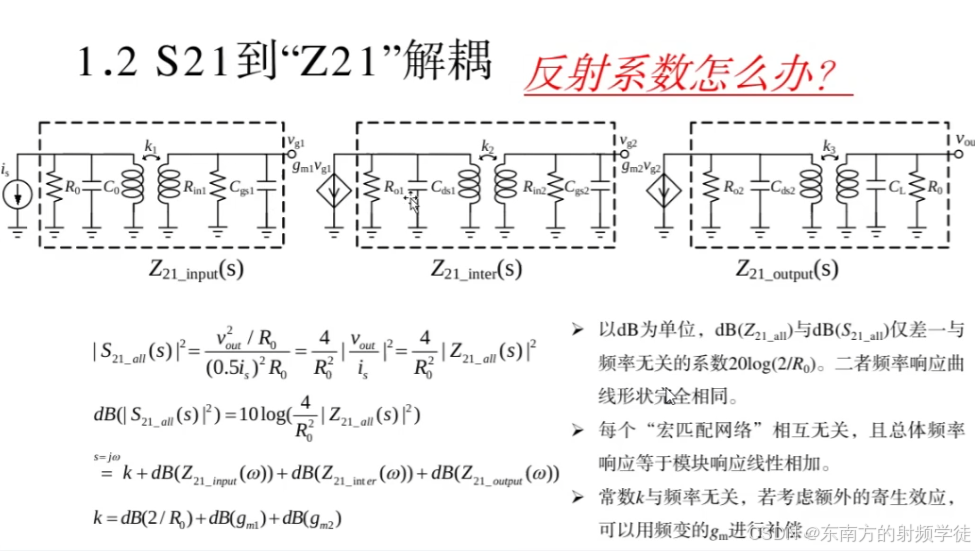
- 这里做了处理,先把戴维宁电路变成诺顿电路is0和R0,同时把简化版的晶体管频变等效小信号模型,其寄生参数变成匹配网络的一部分。这里由于包括了50欧姆,因此Z21就是跨阻增益,它代表了从微波信号源is,传递到Vg1的能力。那么对于级间匹配网络,把跨阻电流源包括到外面去,然后把输出的寄生网络包含到匹配网络中。这样就可以变成电流转电压,电压转电流。所以整个的频率响应就是Z21,整个的Z21就等于
- 这里提到的Z21代表了通过输入端电流源传输到输出端的增益,而S21则代表了输入到输出的传输系数。这样就可以得到下面这个公式:
∣ S 2 1 − a l l ( s ) ∣ 2 = v o u t 2 / R 0 ( 0.5 i s ) 2 R 0 = 4 R 0 2 ∣ v o u t i s ∣ 2 = 4 R 0 2 ∣ Z 2 1 − a l l ( s ) ∣ 2 \mid S_{21_{-}all}(s)\mid^{2}=\frac{v_{out}^{2}/R_{0}}{\left(0.5i_{s}\right)^{2}R_{0}}=\frac{4}{R_{0}^{2}}\mid\frac{v_{out}}{i_{s}}\mid^{2}=\frac{4}{R_{0}^{2}}\mid Z_{21_{-}all}(s)\mid^{2} ∣S21−all(s)∣2=(0.5is)2R0vout2/R0=R024∣isvout∣2=R024∣Z21−all(s)∣2
这里, S 21 S_{21} S21 和 Z 21 Z_{21} Z21的关系说明了两者的增益传递特性。通过计算S参数,可以得出增益,而这个增益又可以与Z参数的平方成正比。
2. 转换公式与增益计算
- dB增益的转换:
d B ( ∣ S 2 1 a l l ( s ) ∣ 2 ) = 10 log ( 4 R 0 2 ∣ Z 2 1 a l l ( s ) ∣ 2 ) = s = j ω k + d B ( Z 2 1 i n p u t ( ω ) ) + d B ( Z 2 1 i n t e r ( ω ) ) + d B ( Z 2 1 o u t p u t ( ω ) ) \begin{aligned}&dB(\mid S_{21_all}(s)\mid^{2})=10\log(\frac{4}{R_{0}^{2}}\mid Z_{21_all}(s)\mid^{2})\\&\overset{s=j\omega}{\operatorname*{=}}k+dB(Z_{21_input}(\omega))+dB(Z_{21_inter}(\omega))+dB(Z_{21_output}(\omega))\end{aligned} dB(∣S21all(s)∣2)=10log(R024∣Z21all(s)∣2)=s=jωk+dB(Z21input(ω))+dB(Z21inter(ω))+dB(Z21output(ω))
总增益等于各部分Z21增益之和,且各部分的Z21相互独立,互不影响。 - 进一步通过频率变换来简化增益分析:
k = d B ( 2 / R 0 ) + d B ( g m 1 ) + d B ( g m 2 ) k=dB(2/R_0)+dB(g_{m1})+dB(g_{m2}) k=dB(2/R0)+dB(gm1)+dB(gm2)
这里,g_m的值可能会随着频率略有变化,但通常是一个接近常数的值。通过此公式,我们能够计算不同频率下的增益变化,并做出相应的调整。
3. Z参数在黑盒模型中的应用
- 黑盒模型:这里提到的黑盒模型(包括 Z 21 _ i n p u t Z_{21\_input} Z21_input, Z 21 _ i n t e r Z_{21\_inter} Z21_inter, 和 Z 21 _ o u t p u t Z_{21\_output} Z21_output)将输入、输出以及各级之间的阻抗视为整体的一部分。通过将阻抗 Z 21 Z_{21} Z21 和跨导增益 g m g_m gm结合,可以简化多级放大器的增益分析,便于进一步的优化。
- 匹配网络的作用:匹配网络的设计目的是使得每一阶段的增益都能在宽带内保持平坦。通过优化匹配网络的阻抗,可以保证在每个频率段内都能获得理想的增益,而不仅仅是让每一级放大器都平坦。
4. 具体应用
- 在实际的放大器设计中,可以用gm1和gm2去修正,因为用负电阻的提取方法提取出来的gm1是高通的,但由于实际版图的寄生效应,刚好会发现最后做出来的东西是低通的。因此如果一开始把模型建成高通,那么在后仿的时候,低通的量就会抵消掉高通的量,刚好变平坦了。
1.3 匹配网络频率响应
-
对于每级的匹配网络,假设term的阻抗是随频率变化的,同样的方式进行拆解,将S21用Z21进行表示
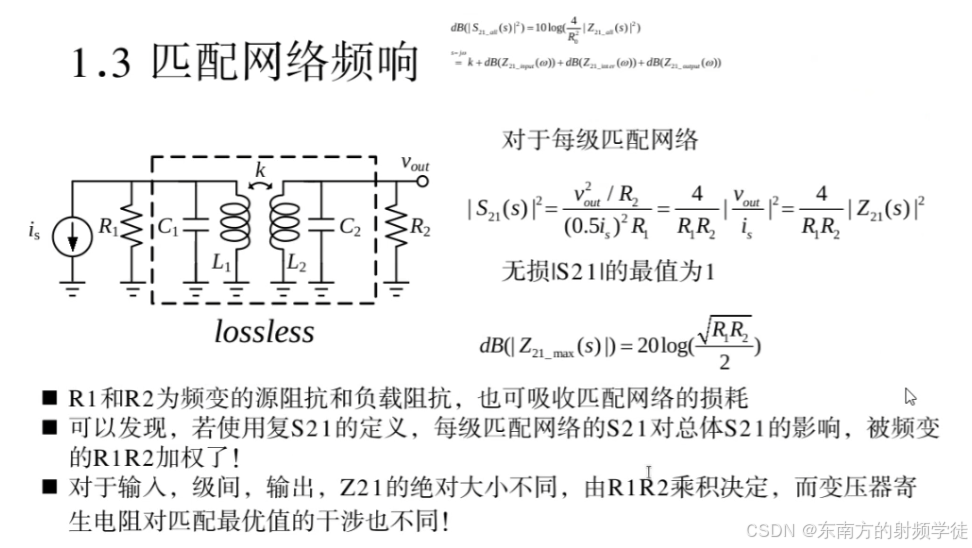
∣ S 21 ( s ) ∣ 2 = v o u t 2 / R 2 ( 0.5 i s ) 2 R 1 = 4 R 1 R 2 ∣ v o u t i s ∣ 2 = 4 R 1 R 2 ∣ Z 21 ( s ) ∣ 2 \mid S_{21}(s)\mid^2=\frac{v_{out}^2/R_2}{\left(0.5i_s\right)^2R_1}=\frac{4}{R_1R_2}\mid\frac{v_{out}}{i_s}\mid^2=\frac{4}{R_1R_2}\mid Z_{21}(s)\mid^2 ∣S21(s)∣2=(0.5is)2R1vout2/R2=R1R24∣isvout∣2=R1R24∣Z21(s)∣2 -
那么对应有损情况下,即L1和L2有损耗,我们可以用R1和R2去吸收掉这些损耗,那么对应虚线部分的电路就是无损情况下的了。
d B ( ∣ Z 21 m a x ( s ) ∣ ) = 20 log ( R 1 R 2 2 ) dB(|Z_{21 max}(s)|)=20\log(\frac{\sqrt{R_1R_2}}{2}) dB(∣Z21max(s)∣)=20log(2R1R2)- 有损情况下,当用R1吸收掉损耗之后,使得变压器的内阻作为极限曲线的一部分,去修正我的极限曲线。
-
那么在无损情况下,其S21是等于1的,因此其最值为1。不可能超过1,因为能量是守恒的。即所有能量都传输到负载端
-
匹配网络的权重影响:
- 由于匹配网络的阻抗( R 1 , R 2 R_1, R_2 R1,R2)随频率变化,导致增益在不同频率下被加权影响。
- 该加权效应会影响整体增益曲线,使得某些频率下增益下降,导致增益带宽受限。
无损匹配网络的极限
-
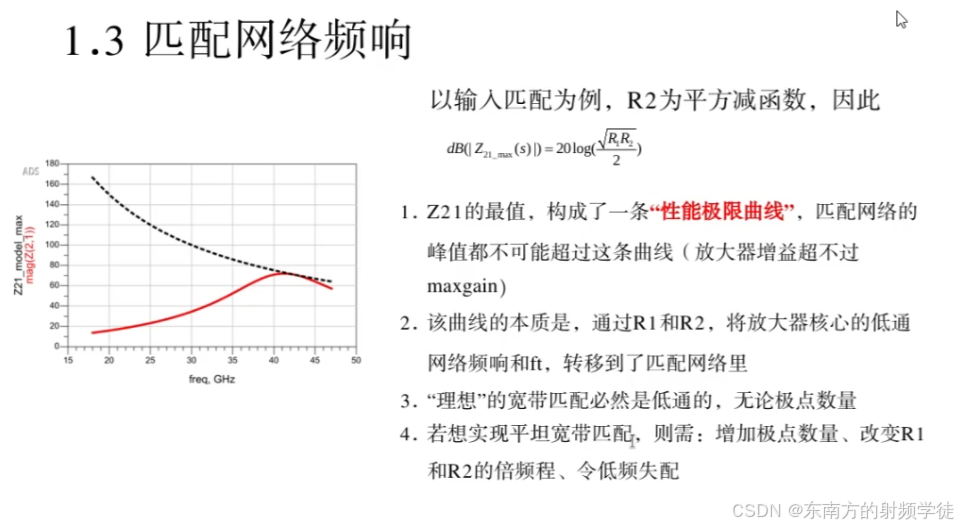
极限增益曲线:
- 取对数后,最大
Z
21
Z_{21}
Z21 的表达式:
d B ( ∣ Z 21 _ m a x ( s ) ∣ ) = 20 log ( R 1 R 2 2 ) dB(|Z_{21\_max}(s)|) = 20 \log \left( \frac{\sqrt{R_1 R_2}}{2} \right) dB(∣Z21_max(s)∣)=20log(2R1R2) - 该公式表明:
- 无损匹配网络的增益不会超过某个极限值,该值取决于匹配网络的输入阻抗 R 1 R_1 R1 和输出阻抗 R 2 R_2 R2。
- 若匹配网络包含损耗(例如寄生电阻、变压器损耗等),那么极限增益将进一步下降。
- 取对数后,最大
Z
21
Z_{21}
Z21 的表达式:
-
如何优化匹配网络?
- 通过合适的 电感、电容匹配,可以提高增益,但 匹配网络的频变特性 需要特别关注,否则增益会随着频率变化而大幅下降。
级联匹配网络的影响
- 级联匹配网络的影响权重不同:
- 由于匹配网络不仅影响单级放大器,还影响整体多级放大器,级间阻抗匹配的影响至关重要。
- 输入、级间和输出匹配网络的权重不同,且输入匹配网络对整体增益的影响更大。
- 变压器寄生阻抗也会对增益极限曲线产生干扰,如果不优化变压器匹配,增益可能大幅下降。
设计匹配网络时的策略
- 合理优化 R1, R2,使其在目标频率范围内尽可能保持恒定,避免频率变化导致增益剧烈波动。
- 考虑变压器匹配网络的寄生损耗,优化变压器模型,确保匹配网络不过度损耗信号能量。
- 使用预训练的匹配参数进行优化,减少设计时间,提高匹配网络的适应性,避免设计超标或不达标的情况。
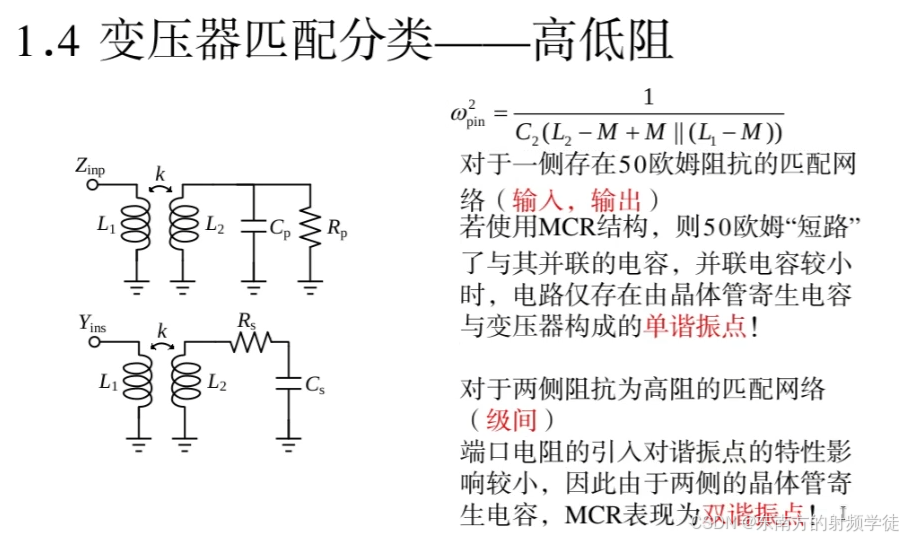
- 如何构成极点?
- 虚线框住的RC电路不能构成极点,因为R0太小了,它几乎吃掉了由is流出的所有电流,而几乎没有电流流过C0,那么由w=1/LC,C没有了则极点就消失了。当寄生足够大的时候,极点消失。
- 因此在源端50欧姆一侧再并联电容或电感,不可能会增加极点。
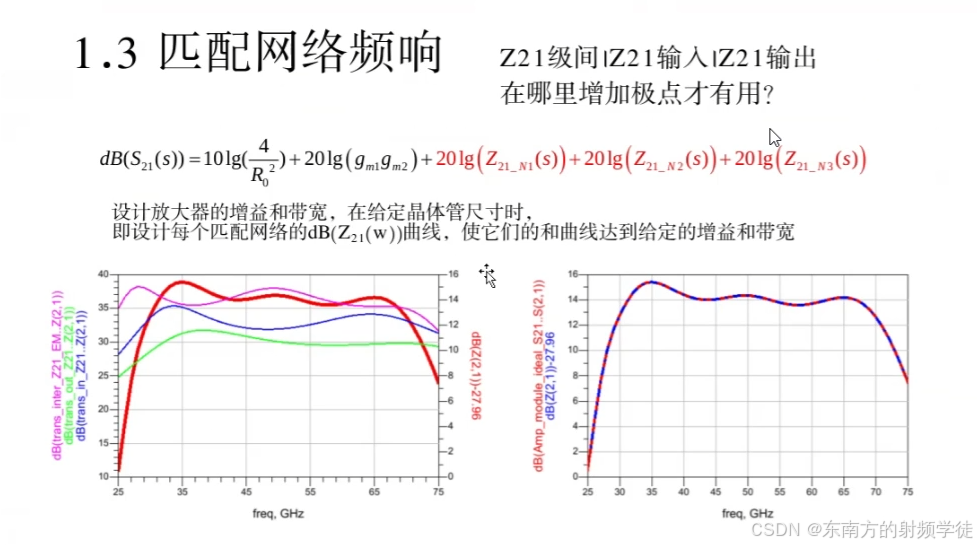
- 但是级间匹配网络,左右两侧都是高阻,这时候再插入一个虚部,其敏感度会很大。这时候如果强行增加Z21的极点数量,就会拉高带宽。
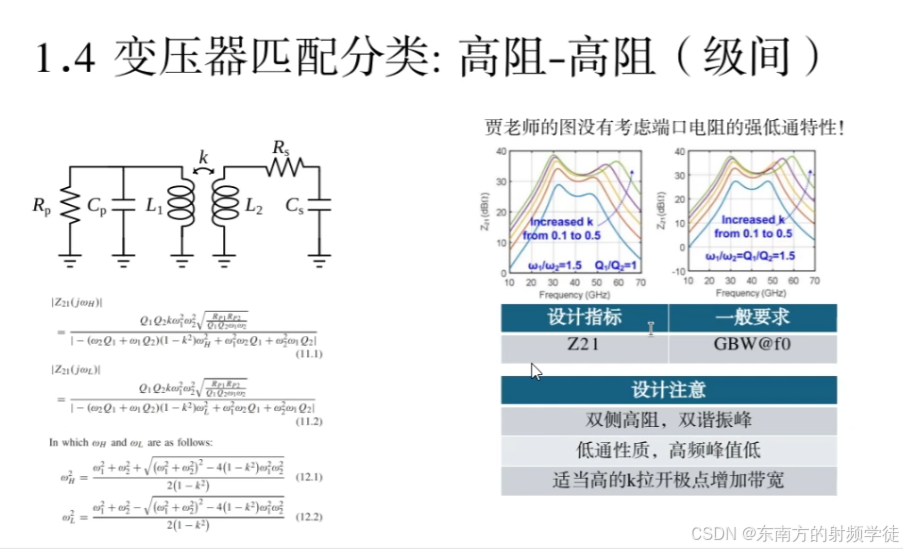
- 对于一个标准的宽带放大器,其任务是把反射系数降到最小,
- 对于左边的Z21曲线图,级间匹配Z21(粉色)做到了3个极点,对应于总Z21曲线(红色)也存在三个极点。但是此时总Z21相对是低通状态,如果想提高高频增益,需要提高第三级Z21(绿色线)
- 然后我们再对变压器匹配类型进行一次分类,根据左右高低阻抗不同进行分类
- 一般以k为自变量去调节改变
- 级间匹配是双谐振点,因为左右两边寄生电阻足够大,所以可以忽略,这时候贾海坤的论文才是成立的。但是这里RP1和RP2没有修正。
- 我们可以发现k越高,两极点距离越远,不管平坦度,可以让中间凹陷下去。
- 而对于输入输出匹配网络,刚好把频率响应放在中心频率,这样整个就是平的。
- 有时候会为了提高放大器的稳定性,加入并联电阻,使得极限曲线变得平滑,即把低频给拉低了,低频变平坦了。
- 输出要考虑loss
- 如果用M9和M8层叠做的时候,会有额外的Cc,起到短通路的作用。本来就像刚才讲的分布式一样,要通过
- 尽量不要使用AP层,65nm的AP层性能太差了。
1.5 实践操作
- 对于这个等效电路,如果仿真单晶体管电路,我们首先要加上一个负电容屏蔽掉Cgd,否则会有弥勒效应出现出输出上。
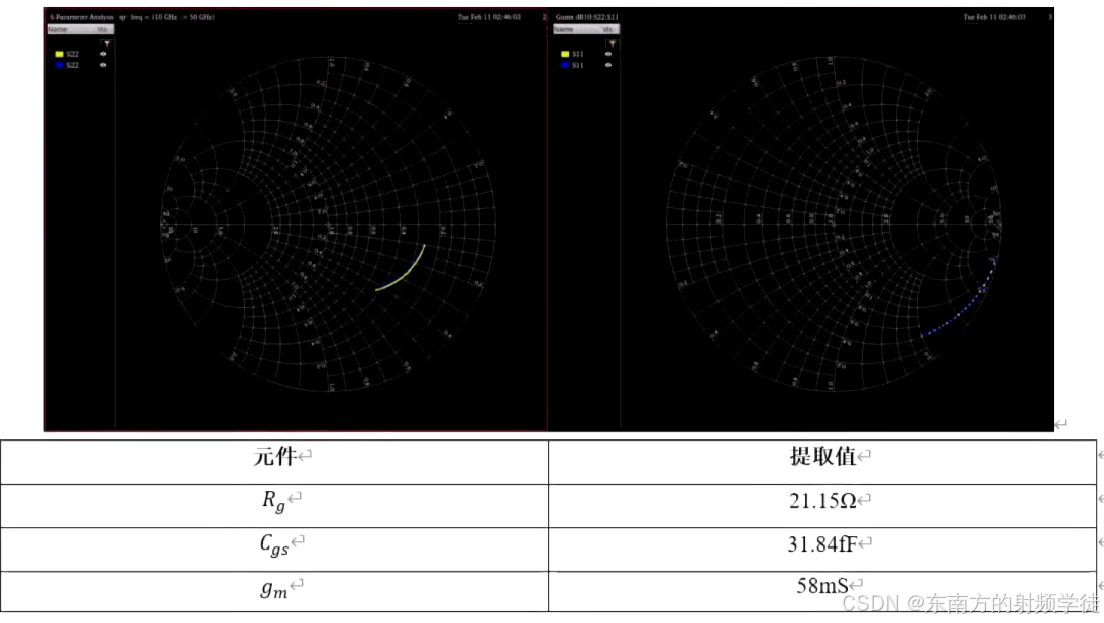
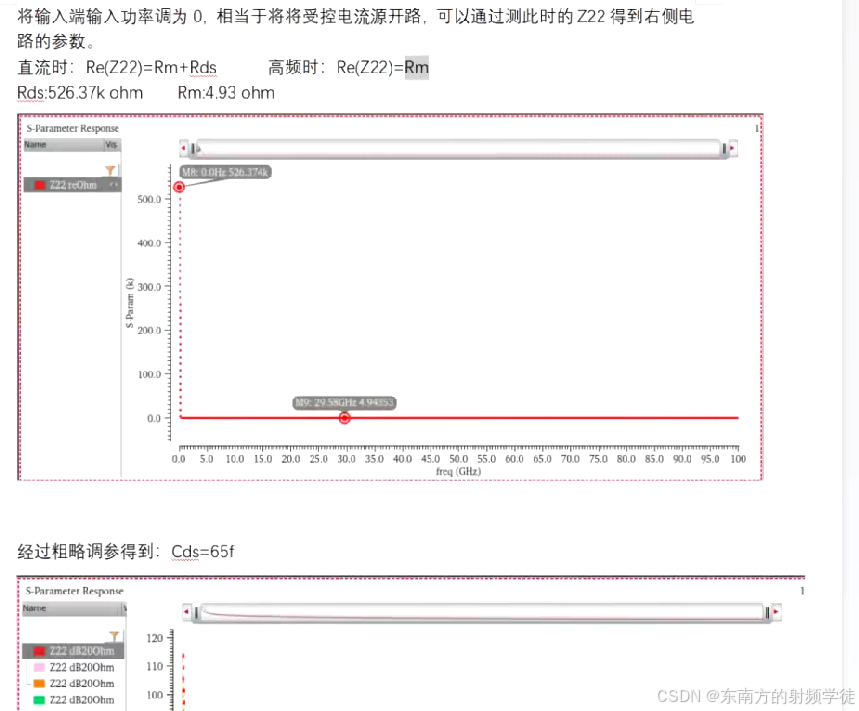
- 我们可以仿真晶体管的Zin,其实部就是Rg,
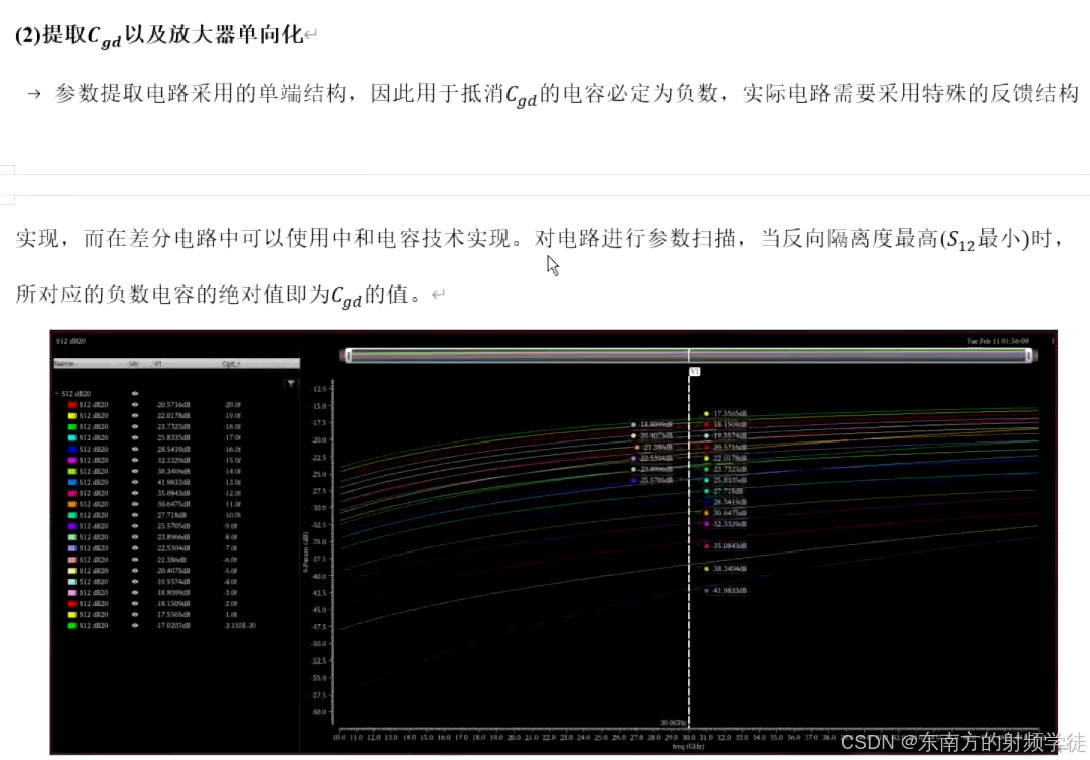
- 对于Rm,我们可以仿真S22,让其显示到Smith chart上,这时候在原理图的漏极加上负电阻,扫描这个负电阻的阻值,直到S22在工作频带内随着频率的变换,在Smith chart上沿着等电导圆在转,说明此时漏极只剩下Rds和Cds了,Rm已经被负电阻给抵消掉了,
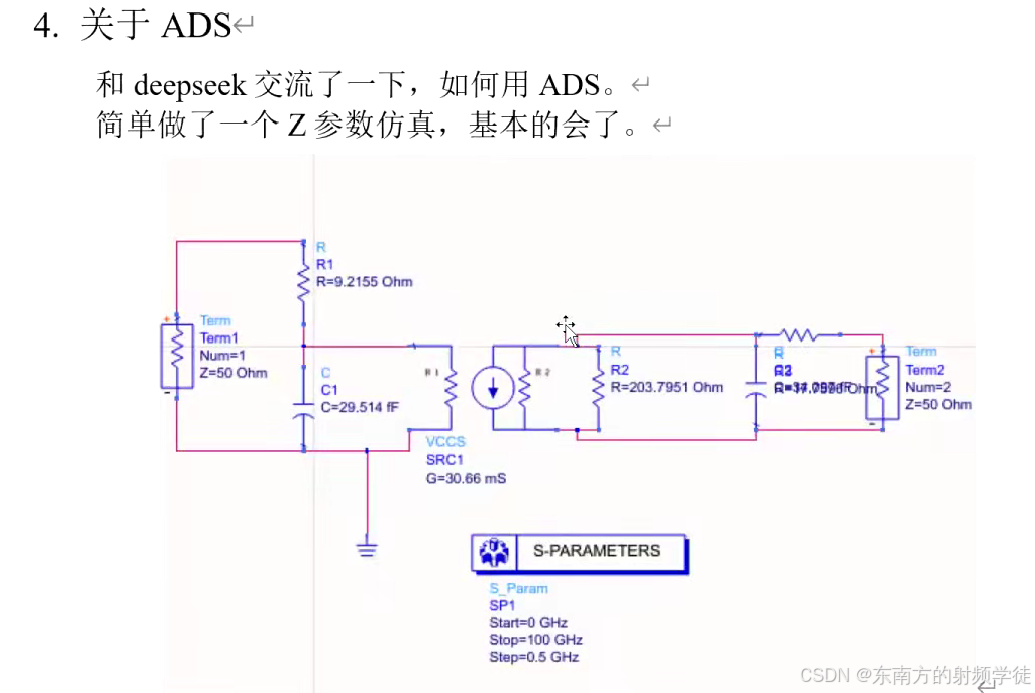
ADS软件中的data access component控件DAC
引用这个控件,使用频变的term,
- 带有中和电容的单晶体管形式
- 由于gm的定义是Ids/vgs的曲线斜率,因此我们可以直接对曲线进行求导得到准确值,而不是用operation point去提取。
- 对于中和电容差分形式