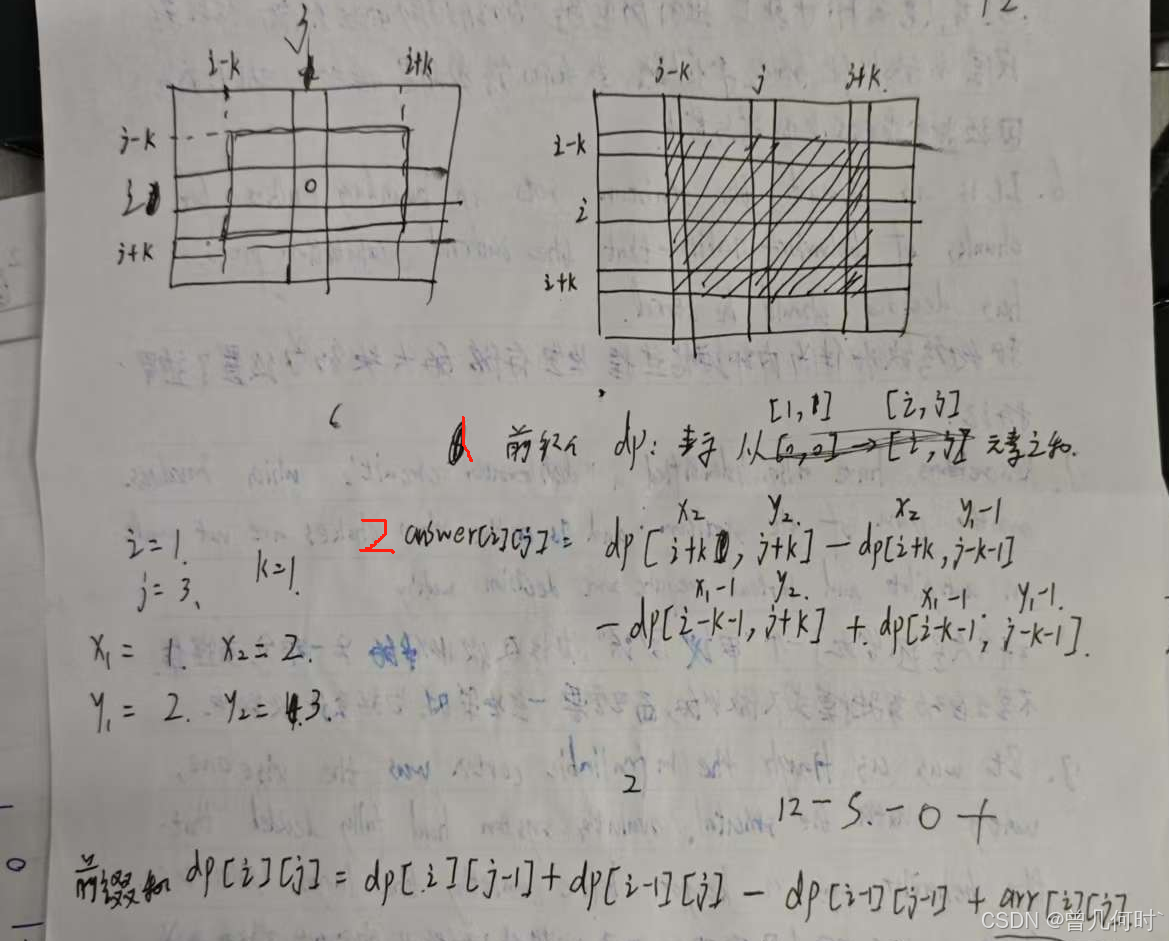
1314. 矩阵区域和
给你一个
m x n的矩阵mat和一个整数k,请你返回一个矩阵answer,其中每个answer[i][j]是所有满足下述条件的元素mat[r][c]的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1 输出:[[12,21,16],[27,45,33],[24,39,28]]示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2 输出:[[45,45,45],[45,45,45],[45,45,45]]提示:
m == mat.lengthn == mat[i].length1 <= m, n, k <= 1001 <= mat[i][j] <= 100
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
// 1、初始化前缀和dp数组
int m = mat.size(), n = mat[0].size();
vector<vector<int>> dp(m+1, vector<int> (n+1));
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++) // dp前缀和数组定义为从[1,1]->[i,j]位置的和
dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + mat[i-1][j-1];
// for(int i = 1; i <= m; i++)
// for(int j = 1; j <= n; j++)
// cout<<dp[i][j]<<" ";
// 2、使用前缀和进行更新answer
vector<vector<int>> ans(m, vector<int> (n));
int x1,y1,x2,y2;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
x1 = i-k < 1 ? 1 : i-k;
y1 = j-k < 1 ? 1 : j-k;
x2 = i+k > m ? m : i+k;
y2 = j+k > n ? n : j+k;
ans[i-1][j-1] = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];
// cout<<ans[i-1][j-1];
}
}
return ans;
}
};