Bootstrap

C++——红黑树

目录

 一、红黑树结点结构

 二、红黑树结构

三、红黑树插入

 四、旋转代码的实现

 五、完整源码

 

 

 一、红黑树结点结构

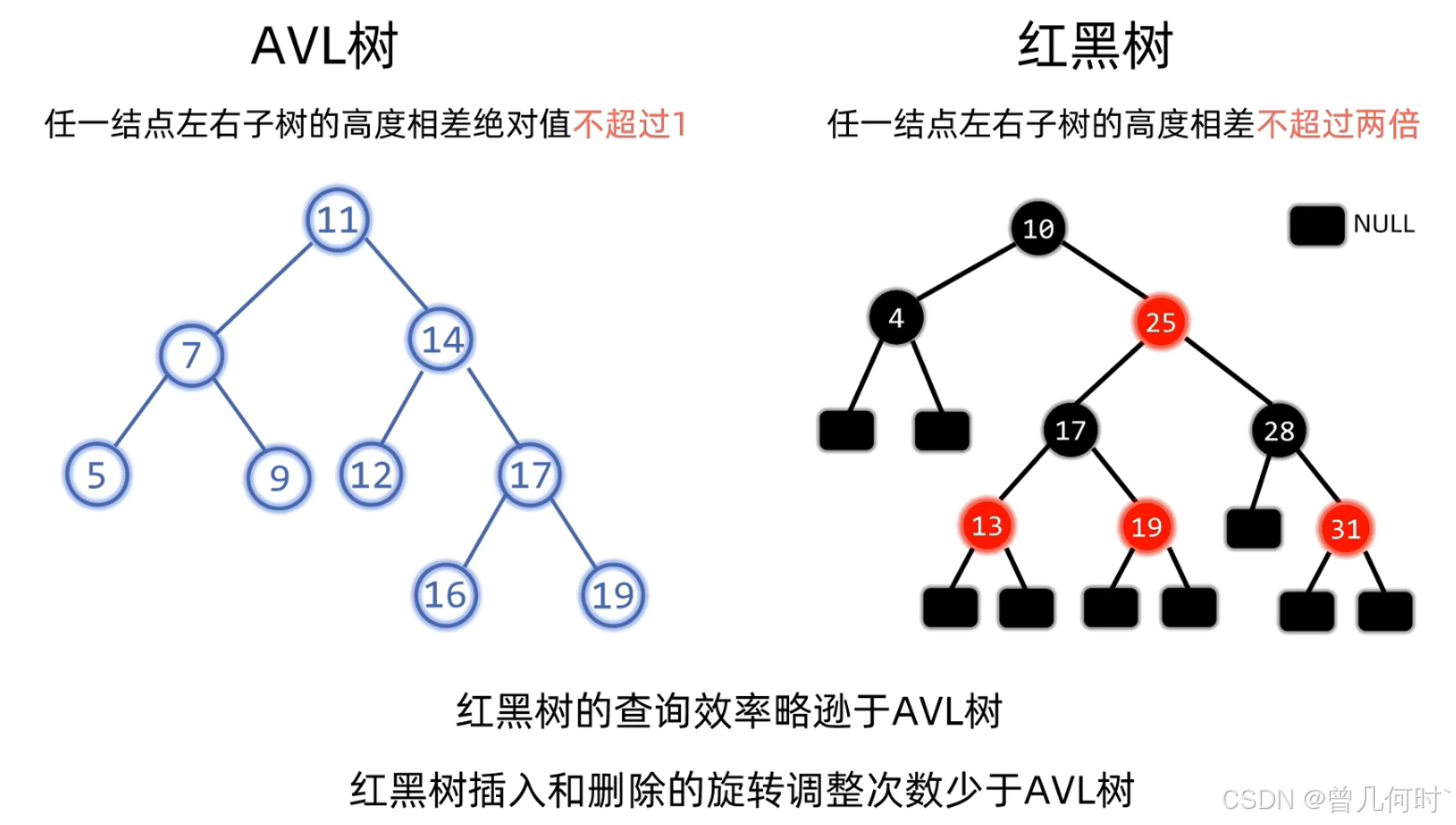
与AVL树相同的使用三叉链表实现，多了一个枚举类型的成员，用来表示每个结点的红黑颜色。

enum Color
{
	RED,
	BLACK
};

template<class K, class V>
class RBTreeNode
{
public:
	std::pair<K, V> _kv;
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	Color _col;

	RBTreeNode(const std::pair<K, V> kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};

 二、红黑树结构

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
    ………………
private:
    Node* _root = nullptr;
};

三、红黑树插入

	bool Insert(const std::pair<K, V> kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		// 1、迭代遍历寻找插入位置
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				std::cout << "该 [" << cur->_kv.first << "] 结点已经存在，插入失败" << std::endl;
				return false;
			}
		}

		// 2、找到插入位置之后，新建结点进行接入
		cur = new Node(kv);
		cur->_parent = parent;
		cur->_col = RED;
		if (kv.first > parent->_kv.first)
			parent->_right = cur;
		else
			parent->_left = cur;

		// 3、对红黑树进行处理  先看父亲是否为黑色
		//	如果父亲为黑色，那么直接插入结束
		if (parent && parent->_col == BLACK) 
			return true;	
            
           4、父亲为红色的条件下，看叔叔颜色
		// 下来的结果父亲只能是红色，那么根据不红红（父子不能同时为红色）
		// 不断的向上更新 父子不能同时为红色  所以使用while
		while (parent && parent->_col == RED)
		{
			// 先看父亲红不红，再看叔叔红不红，
               但是要想看叔叔红不红，必须要清楚叔叔在左边还是右边，
               因此需要知道爷爷和父亲的关系，才能确定叔叔的位置
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)
				{
				    叔叔为红色，叔父爷变色，
                    cur更新为爷爷，让parent更新为爷爷的父亲，
                    再次进行红黑树判定
					uncle->_col = BLACK;
					parent->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{   
                    旋转+变色之后 需要break跳出循环
					// 叔叔为黑色，进行旋转+变色
					if (cur == parent->_left)
					{
                        单旋 爷父 变色
                        对于爷的情况 均为变红
                        对于父子情况 均为变黑
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}

					else
					{
                        双旋 爷孙 变色
						RotateLR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					uncle->_col = BLACK;
					parent->_col = BLACK; 
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					// 叔叔为黑色，进行旋转+变色
					if (cur == parent->_left)
					{
						RotateRL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}

 四、旋转代码的实现

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		// 更新subL的父指针，俩种情况
		if (parent == _root)
		{
			subL->_parent = nullptr;
			_root = subL;
		}
		else
		{
			Node* ppNode = parent->_parent;	// 需要找parent的父亲结点
			if (parent == ppNode->_left)	// 并且判断parent与其父亲的左右关系
				ppNode->_left = subL;
			else
				ppNode->_right = subL;
			subL->_parent = ppNode;

		}
		// 更新subL的右
		subL->_right = parent;

		// 更新parent的父和左指针
		parent->_parent = subL;
		parent->_left = subLR;

		// 再subLR存在的情况下 更新它的_parent
		if (subLR)
		{
			subLR->_parent = parent;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		// 更新了subR的_parent指针
		if (parent == _root)
		{
			subR->_parent = nullptr;
			_root = subR; // 只有parent为根的时候才更新subR为根
		}
		else
		{
			Node* ppNode = parent->_parent;
			if (ppNode->_left == parent)
				ppNode->_left = subR;
			else
				ppNode->_right = subR;
			subR->_parent = ppNode;
		}
		// 更新subR的_left指针
		subR->_left = parent;

		// 更新parent的父和右
		parent->_parent = subR;
		parent->_right = subRL;

		// 更新suRL
		if (subRL)
		{
			subRL->_parent = parent;
		}
	}


	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		RotateL(subL);
		RotateR(parent);
	}
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		RotateR(subR);
		RotateL(parent);
	}

 五、完整源码

#include<iostream>
#include<queue>
#include<vector>
#include<assert.h>
// using namespace std;

enum Color
{
	RED,
	BLACK
};

template<class K, class V>
class RBTreeNode
{
public:
	std::pair<K, V> _kv;
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	Color _col;

	RBTreeNode(const std::pair<K, V> kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	bool Insert(const std::pair<K, V> kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		// 1、迭代遍历寻找插入位置
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				std::cout << "该 [" << cur->_kv.first << "] 结点已经存在，插入失败" << std::endl;
				return false;
			}
		}

		// 2、找到插入位置之后，新建结点进行接入
		cur = new Node(kv);
		cur->_parent = parent;
		cur->_col = RED;
		if (kv.first > parent->_kv.first)
			parent->_right = cur;
		else
			parent->_left = cur;

		// 3、对红黑树进行处理  先看父亲是否为黑色
		//	如果父亲为黑色，那么直接插入结束
		if (parent && parent->_col == BLACK) 
			return true;	

		// 下来的结果父亲只能是红色，那么根据不红红（父子不能同时为红色）
		// 不断的向上更新父子不能同时为红色  所以使用while
		while (parent && parent->_col == RED)
		{
			// 先看父亲红不红，再看叔叔红不红，但是要想看叔叔红不红，必须要清楚叔叔在左边还是右边，因此需要知道爷爷和父亲的关系，才能确定叔叔的位置
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)
				{
					// 叔叔为红色，叔父爷变色，爷爷指针更新为cur，让parent更新为cur的父亲，再次进行红黑树判定
					uncle->_col = BLACK;
					parent->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					// 叔叔为黑色，进行旋转+变色
					if (cur == parent->_left)
					{
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}

					else
					{
						RotateLR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					uncle->_col = BLACK;
					parent->_col = BLACK; 
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					// 叔叔为黑色，进行旋转+变色
					if (cur == parent->_left)
					{
						RotateRL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		// 更新subL的父指针，俩种情况
		if (parent == _root)
		{
			subL->_parent = nullptr;
			_root = subL;
		}
		else
		{
			Node* ppNode = parent->_parent;	// 需要找parent的父亲结点
			if (parent == ppNode->_left)	// 并且判断parent与其父亲的左右关系
				ppNode->_left = subL;
			else
				ppNode->_right = subL;
			subL->_parent = ppNode;

		}
		// 更新subL的右
		subL->_right = parent;

		// 更新parent的父和左指针
		parent->_parent = subL;
		parent->_left = subLR;

		// 再subLR存在的情况下 更新它的_parent
		if (subLR)
		{
			subLR->_parent = parent;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		// 更新了subR的_parent指针
		if (parent == _root)
		{
			subR->_parent = nullptr;
			_root = subR; // 只有parent为根的时候才更新subR为根
		}
		else
		{
			Node* ppNode = parent->_parent;
			if (ppNode->_left == parent)
				ppNode->_left = subR;
			else
				ppNode->_right = subR;
			subR->_parent = ppNode;
		}
		// 更新subR的_left指针
		subR->_left = parent;

		// 更新parent的父和右
		parent->_parent = subR;
		parent->_right = subRL;

		// 更新suRL
		if (subRL)
		{
			subRL->_parent = parent;
		}
	}


	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		RotateL(subL);
		RotateR(parent);
	}
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		RotateR(subR);
		RotateL(parent);
	}

	void Print()
	{
		CX_Print(_root);
	}
	void CX_Print(Node* parent)
	{
		std::queue<Node*> q;
		std::vector<Node*> res;
		q.push(parent);
		while (!q.empty())
		{
			Node* cur = q.front();
			res.push_back(cur);
			q.pop();
			if (cur->_left)
				q.push(cur->_left);
			if (cur->_right)
				q.push(cur->_right);
		}
		for (Node* key : res)
		{
			std::cout << key->_kv.first << " ";
		}
		std::cout << std::endl;
	}
	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			// 和二叉排序树类似，不过这里的结点是 const pair<K, V>& _key 
			// 所以比较的时候使用 cur->_key.first 来访问第一个关键字
			if (cur->_kv.first > key)
				cur = cur->_left;
			else if (cur->_kv.first < key)
				cur = cur->_right;
			else
				return cur;
		}
		return nullptr;
	}

private:
	Node* _root = nullptr;
};


void TestAVLTreeL()
{
	RBTree<int, int> t;

	t.Insert({ 10, 1 });
	t.Insert({ 12, 1 });
	t.Insert({ 8, 1 });
	t.Insert({ 7, 1 });
	t.Insert({ 9, 1 });
	t.Print();
	t.Insert({ 6, 1 });

	t.Print();
}

void TestAVLTreeR()
{
	RBTree<int, int> t;

	t.Insert({ 10, 1 });
	t.Print();
	t.Insert({ 12, 1 });
	t.Print();
	t.Insert({ 8, 1 });
	t.Print();
	t.Insert({ 11, 1 });
	t.Insert({ 14, 1 });
	t.Print();
	t.Insert({ 13, 1 });

	t.Print();
}


#if 0
void TestAVLTree1()
{
	AVLTree<int, int> t;
	// 常规的测试⽤例
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	// 特殊的带有双旋场景的测试⽤例
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16 };
	for (auto e : a)
	{
		t.Insert({ e, e });
		t.Print();
		cout << endl;
	}
	// t.Insert({14,1});  RL
	t.Insert({ 17,1 });

	t.Print();
	if (t.Is_Balance_Tree())
		cout << "is balance" << endl;
	else
		cout << "no balance" << endl;
}

#endif

void TestAVLTree2()
{
	const int N = 10000;
	std::vector<int> v;
	v.reserve(N);
	srand(time(0));
	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
	}
	size_t begin2 = clock();
	RBTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(std::make_pair(e, e));
	}
	size_t end2 = clock();
	std::cout << "Insert:" << end2 - begin2 << std::endl;
	t.Print();
	/*if (t.Is_Balance_Tree())
		std::cout << "is balance" << std::endl;
	else
		std::cout << "no balance" << std::endl;*/
	// std::cout << "Height:" << t.Height() << std::endl;
	// cout << "Size:" << t.Size() << endl;
	size_t begin1 = clock();
	// 确定在的值
	for (auto e : v)
	{
		t.Find(e);
	}
	// 随机值
	/*for (size_t i = 0; i < N; i++)
	{
		t.Find((rand() + i));
	}
	size_t end1 = clock();
	cout << "Find:" << end1 - begin1 << endl;*/
}

int main()
{

	//TestAVLTreeR();
    // TestAVLTreeL();
    // TestAVLTree1();
	TestAVLTree2();
	return 0;
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
[源码解析] 并行分布式框架 Celery 之 worker 启动 (2)
写点程序员离职的心得
华为OD机考统一考试C卷 全量和已占用字符集 、字符串统计（C++题解）
基于DSP280049C的正点原子PMSM电机驱动（二）：FOC文件的建立与开环代码编写
【C++】list 迭代器详解和模拟实现
TEXTURE COMPRESSION TECHNIQUES
机器学习的模型类型（Model Types）
【Python爬虫(24)】Redis：Python爬虫的秘密武器
华为OD机试 - 求最小公倍数（Python/JS/C/C++ 牛客练习题 HJ108）
python中subprocess.Popen的args和shell参数的使用
;