💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
本文主要介绍了使用离散平稳小波变换的简单图像融合算法。离散平稳小波变换是一种有效的信号处理工具,在图像融合领域具有重要应用。该算法通过对源图像进行离散平稳小波变换,将图像分解为不同尺度和方向的子带。然后,根据特定的融合规则对各个子带进行融合处理,以保留源图像中的重要特征信息。融合后的子带再通过逆离散平稳小波变换重构得到融合后的图像。这种简单的图像融合算法具有计算效率高、易于实现等优点,能够在一定程度上提高图像的质量和信息量,为图像分析和处理提供了一种有效的手段。
一、引言
图像融合是图像处理领域中的一个重要研究方向,旨在将两幅或多幅图像中的有用信息综合到一幅图像中,以提高图像信息的利用率和视觉效果。离散平稳小波变换(DSWT)作为一种有效的多尺度分析工具,在图像融合中得到了广泛应用。
二、离散平稳小波变换(DSWT)基础
-
定义与特点
- DSWT是离散小波变换(DWT)的一种变体,它在处理图像时能够保持信号的稳态特性,即在不同尺度上保持信号的能量守恒。
- DSWT保留了小波系数的所有平移不变性,这意味着即使输入图像有轻微的平移或位移,变换后的系数也会保持相似,这对于图像融合特别重要。
-
与DWT的区别
- 传统的DWT在图像变换过程中可能会改变小波系数的平移特性,而DSWT则能够保持这种平移不变性。
三、基于DSWT的图像融合算法
-
算法步骤
- 预处理:对原始图像进行去噪、增强等预处理,以提高图像质量。
- 配准:对预处理后的图像进行配准,确保待融合图像在空间位置上的一致性,为后续的小波分解和融合处理提供准确的输入。
- DSWT分解:对配准后的图像进行DSWT分解,得到一系列不同尺度和方向的子带图像。这些子带图像包含了图像在不同频率和方向上的细节信息。
- 融合规则设计:根据不同的应用需求和图像特性,设计合适的融合规则。例如,在高频域内,可以选择多源图像邻域平均绝对值较大的系数作为重要小波系数;在低频域内,可以通过对多源图像的逼近系数进行加权平均来得到新的逼近系数。
- 子带图像融合:根据设计的融合规则,对分解得到的子带图像进行融合处理。通过合并不同图像的互补信息,得到融合后的子带图像。
- DSWT逆变换:对融合后的子带图像进行DSWT逆变换,将融合后的子带图像恢复到原始图像空间,得到最终的融合图像。
-
算法优势
- 多尺度分析:DSWT能够将图像分解到不同尺度和方向上,使得图像信息在不同尺度上得以分离和提取,有利于后续的融合处理。
- 信息互补:通过融合不同图像的互补信息,可以提高融合图像的信息量和视觉效果。
- 灵活性高:融合规则可以根据具体需求进行设计,具有较强的灵活性和适应性。
- 效果好:与传统的图像融合方法相比,基于DSWT的图像融合方法通常能够取得更好的融合效果,如更高的清晰度、更丰富的细节信息等。
四、实验结果与分析
为了验证基于DSWT的图像融合算法的有效性,可以进行一系列实验。通过对比融合前后的图像质量、信息量等指标,可以评估算法的性能。例如,可以利用均方根误差(RMSE)、均方误差(MSE)等客观评价指标来量化融合效果。此外,还可以通过主观观察来评估融合图像的视觉效果。
五、结论与展望
基于DSWT的图像融合算法在图像处理领域具有广泛的应用前景。通过设计合适的融合规则并对分解得到的子带图像进行融合处理,可以得到具有更高信息量和更好视觉效果的融合图像。未来研究可以进一步探索更高效的融合规则和优化算法,以提高图像融合的性能和效率。
📚2 运行结果
主函数部分代码:
close all;
clear all;
home;
% insert images
im1 = double(imread('saras51.jpg'));
im2 = double(imread('saras52.jpg'));
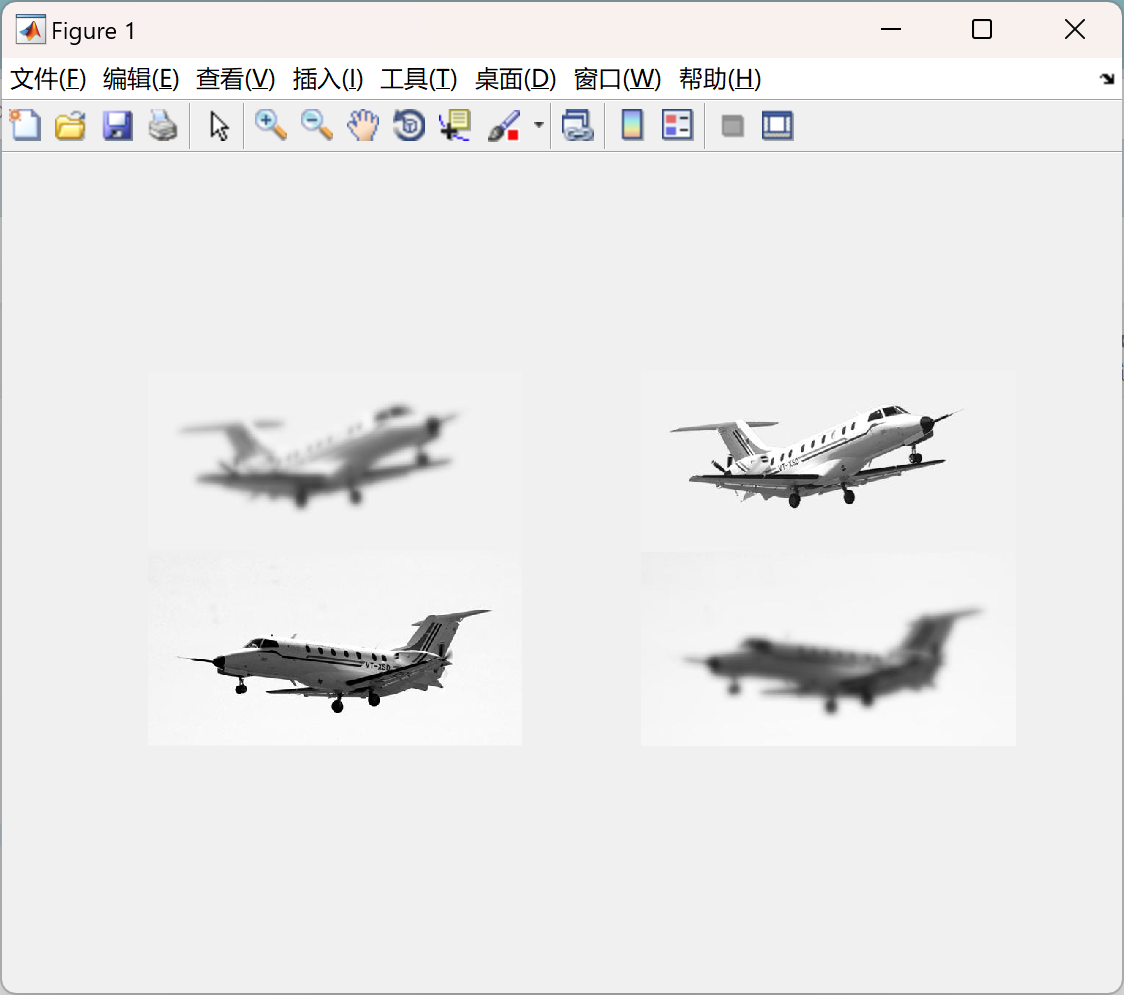
figure(1);
subplot(121);imshow(im1,[]);
subplot(122);imshow(im2,[]);
% image decomposition using discrete stationary wavelet transform
[A1L1,H1L1,V1L1,D1L1] = swt2(im1,1,'sym2');
[A2L1,H2L1,V2L1,D2L1] = swt2(im2,1,'sym2');
% fusion start
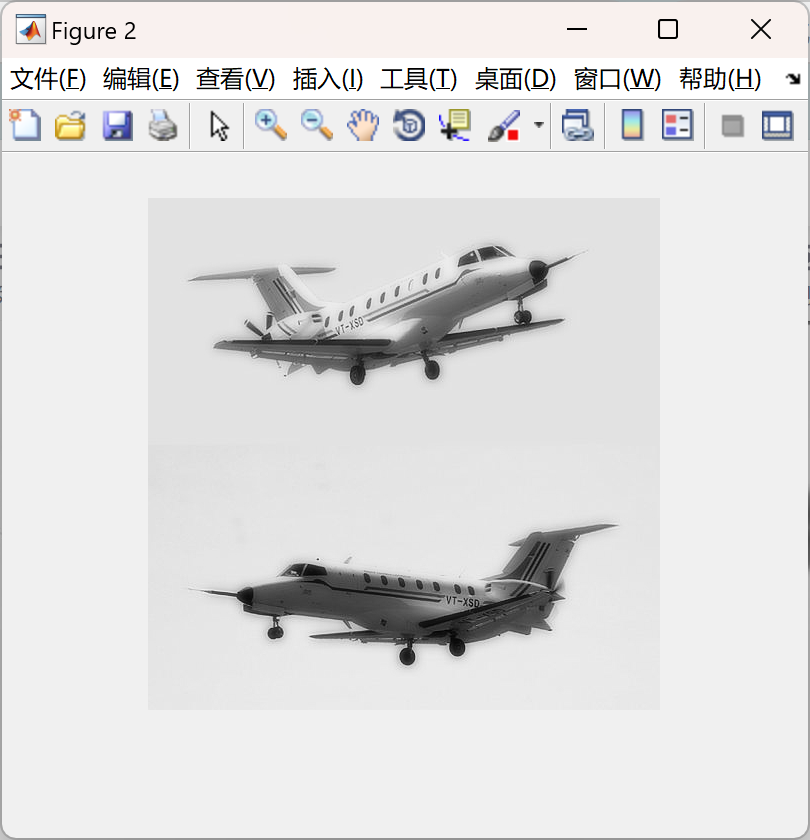
AfL1 = 0.5*(A1L1+A2L1);
D = (abs(H1L1)-abs(H2L1))>=0;
HfL1 = D.*H1L1 + (~D).*H2L1;
D = (abs(V1L1)-abs(V2L1))>=0;
VfL1 = D.*V1L1 + (~D).*V2L1;
D = (abs(D1L1)-abs(D2L1))>=0;
DfL1 = D.*D1L1 + (~D).*D2L1;
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]王淑香,金飞,林雨准,等.联合光谱和空间双尺度细节注入的遥感图像融合[J/OL].光子学报,1-12[2024-11-09].http://kns.cnki.net/kcms/detail/61.1235.O4.20241108.1340.026.html.
[2]郭业才,阳刚,毛湘南.一种融合Transformer的多尺度结构图像去模糊方法[J/OL].电光与控制,1-9[2024-11-09].http://kns.cnki.net/kcms/detail/41.1227.TN.20241108.0947.011.html.