目录
1.零元
设零元为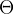
左零元:看一整行元素是否等于表头;右零元:一整列元素是否等于表头。如下图所示,b为左零元。
2.幺元(单位元)
设幺元为e,根据幺元的性质,对于表中任意元素x,都有x*e=e*x=x。
如下图所示,左零元找行与表头相同的,右零元找列与表头相同的。所以下表可以看出零元为a
3.逆元
设逆元为y,根据逆元的性质,对于表中任意元素x,都有x*y=y*x=a(单位元)
如下图所示,找运算结果为a(单位元)的。a*a=a,b*b=a,c*c=a,d*d=a。所以a的逆元为a,b的逆元为b,c的逆元为c,d的逆元为d
4.幂等元
设幂等元为a,则a*a=a,如下图所示,幂等元就是a。
注意:在群中,单位元是唯一的幂等元。但是在半群或者幺半群中就不一定了。
5.某运算是否满足交换律:
看表是否对称:由于下表对称,所以*运算符合交换律
6.某运算是否满足幂等律:
如果对于运算表主对角线上的每一个元素, 都等于其所在行和列表头对应的元素,就满足幂等律。比如,若集合S = {a, b, c},运算表中主对角线元素依次是a,b,c,那就满足幂等律;
如下表就不满足幂等律
7.某运算是否满足消去律:
左可消去元:查看a对应行的运算结果,若无相同元素,则a是左可消去元。
右可消去元:查看a对应列的运算结果,若无相同元素,则a是右可消去元。
可以做下面的验证:右消去元同理
8.某运算是否满足结合律:
可以用穷举法,但是穷举时可以跳过零元和单位元,零元和单位元必满足结合律。如下图所示,有单位元a,无零元,跳过单位元。b,c,d是否满足结合律:(b*c)*d=b*(c*d) ;(b*d)*c=b*(d*c),所以满足结合律。




