直接上题目。
题目:买卖股票的最佳时机 2
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
题目分析:
在已知票价的情况下让利润最大,那么只要有利润就买卖即可。
public class Solution {
public int MaxProfit(int[] prices) {
int res=0;
for(int i=0;i<prices.Length-1;i++){
if(prices[i+1]>prices[i]){//后面的票价高于前面,有利润
res+=(prices[i+1]-prices[i]);
}
}
return res;
}
}题目:跳跃游戏
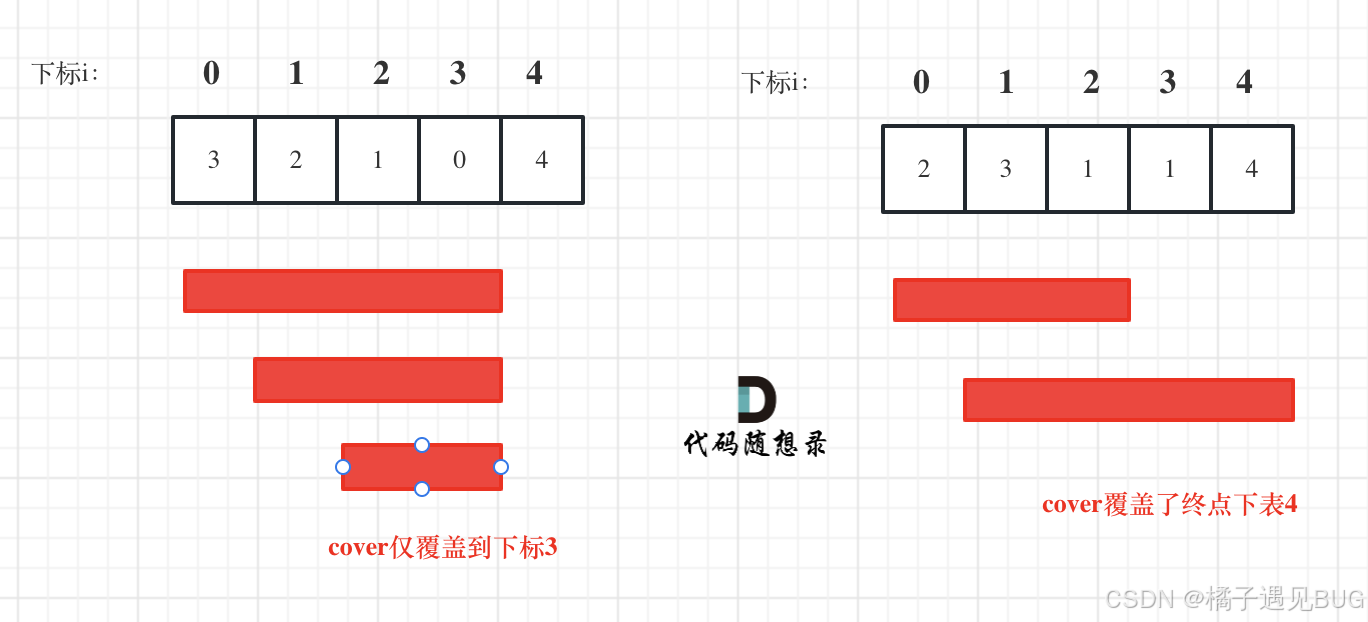
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
题目分析:
每个位置能跳的选择有很多,但是最大的范围是固定的。而最后求能否到达最后位置,也只需要关心我能跳跃的范围能否覆盖到最后的位置,就像这样。
public class Solution {
public bool CanJump(int[] nums) {
if(nums.Length==1) return true;
int cover=0;//当前可覆盖的最大范围
for(int i=0;i<=cover;i++){
cover=Math.Max(i+nums[i],cover);
if(cover>=nums.Length-1){
return true;
}
}
return false;
}
}题目:跳跃游戏 2
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
题目分析:
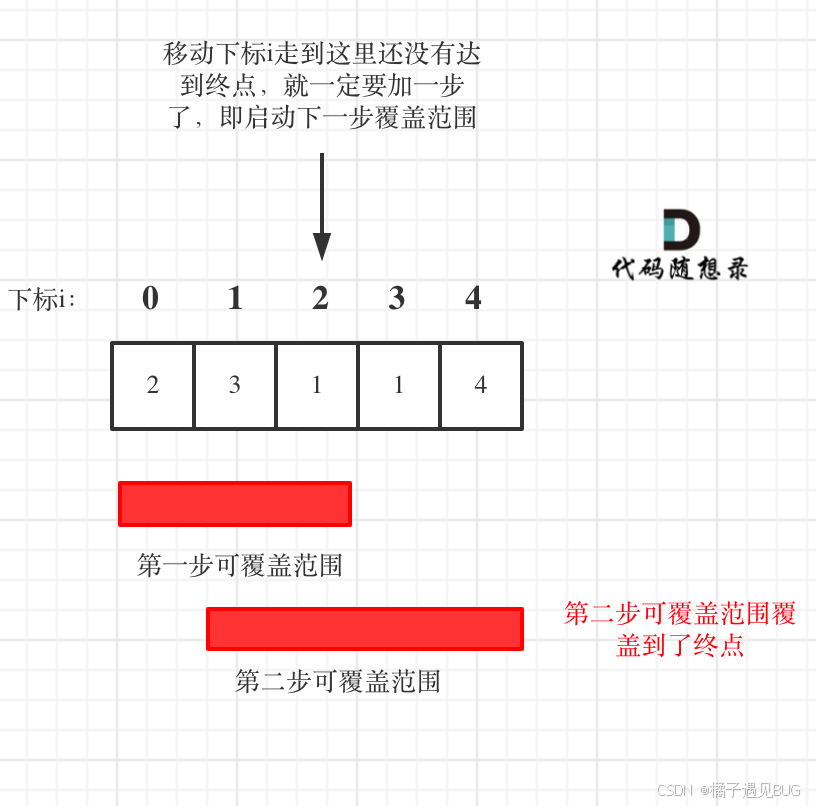
使用最少步数到达最后,和上一题的思路一样,主要看范围。关键是这个步数要怎么计算呢?
从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数!
这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
public class Solution {
public int Jump(int[] nums) {
int res=0;
if(nums.Length==1) return 0;
int curDistance=0;
int nextDistance=0;
for(int i=0;i<nums.Length-1;i++){
nextDistance=Math.Max(i+nums[i],nextDistance);//更新下一步的最大范围
if(i==curDistance)//i到达这一步的最大范围,更新步数
{
res++;
curDistance=nextDistance;
if(nextDistance>=nums.Length-1){
break;
}
}
}
return res;
}
}题目:K次取反后最大化的数组和
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标
i并将nums[i]替换为-nums[i]。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
题目分析:
按照题目的意思模拟即可,很好理解。
public class Solution {
public int LargestSumAfterKNegations(int[] nums, int k) {
int res=0;
Array.Sort(nums,(a,b)=>Math.Abs(b)-Math.Abs(a));
for (int i = 0; i < nums.Length; i++)//尽可能的把小的负数变正数
{
if (nums[i] < 0 && k > 0)
{
nums[i] *= -1;
k--;
}
}
//剩余的k是奇数,选最小的正数取反
if (k % 2 == 1) nums[nums.Length - 1] *= -1;
foreach (var item in nums) res += item;
return res;
}
}题目:加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
题目分析:
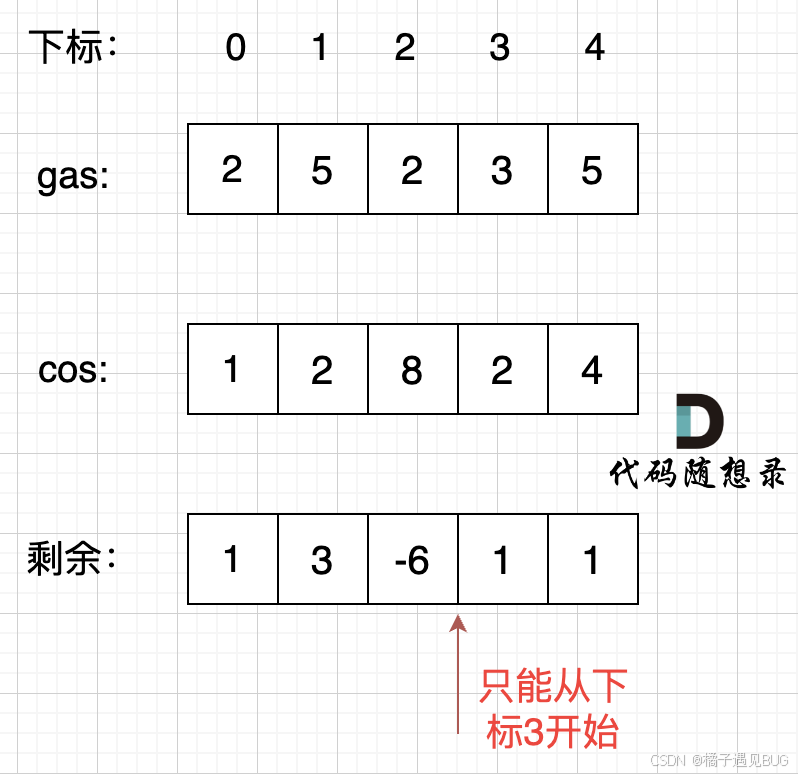
首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
如图:
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新i,那么起始位置又变成新的i+1了。
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢? 如图:
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择起始位置了。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
public class Solution {
public int CanCompleteCircuit(int[] gas, int[] cost) {
int start=0;
int curSum=0;
int totalSum = 0;//剩余油量和
for(int i=0;i<gas.Length;i++){
curSum+=gas[i]-cost[i];
totalSum+=gas[i]-cost[i];
if (curSum < 0) { // 当前累加rest[i]和 curSum一旦小于0
start = i + 1; // 起始位置更新为i+1
curSum = 0; // curSum从0开始
}
}
if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
return start;
}
}题目:柠檬水找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
题目分析:
有如下三种情况:
- 情况一:账单是5,直接收下。
- 情况二:账单是10,消耗一个5,增加一个10
- 情况三:账单是20,优先消耗一个10和一个5,如果不够,再消耗三个5
模拟过程即可
public class Solution {
public bool LemonadeChange(int[] bills) {
int five = 0, ten = 0, twenty = 0;//手上的金额
foreach (var bill in bills)
{
if (bill == 5) five++;
if (bill == 10)
{
if (five == 0) return false;
five--;
ten++;
}
if (bill == 20)
{
if (ten > 0 && five > 0)
{
ten--;
five--;
twenty++;
}
else if (five >= 3)
{
five -= 3;
twenty++;
}
else
{
return false;
}
}
}
return true;
}
}除此之外,还有两题,我没理解,这里就写了。
对于更详细的解析与其他语言的代码块,可以去代码随想录上查看。