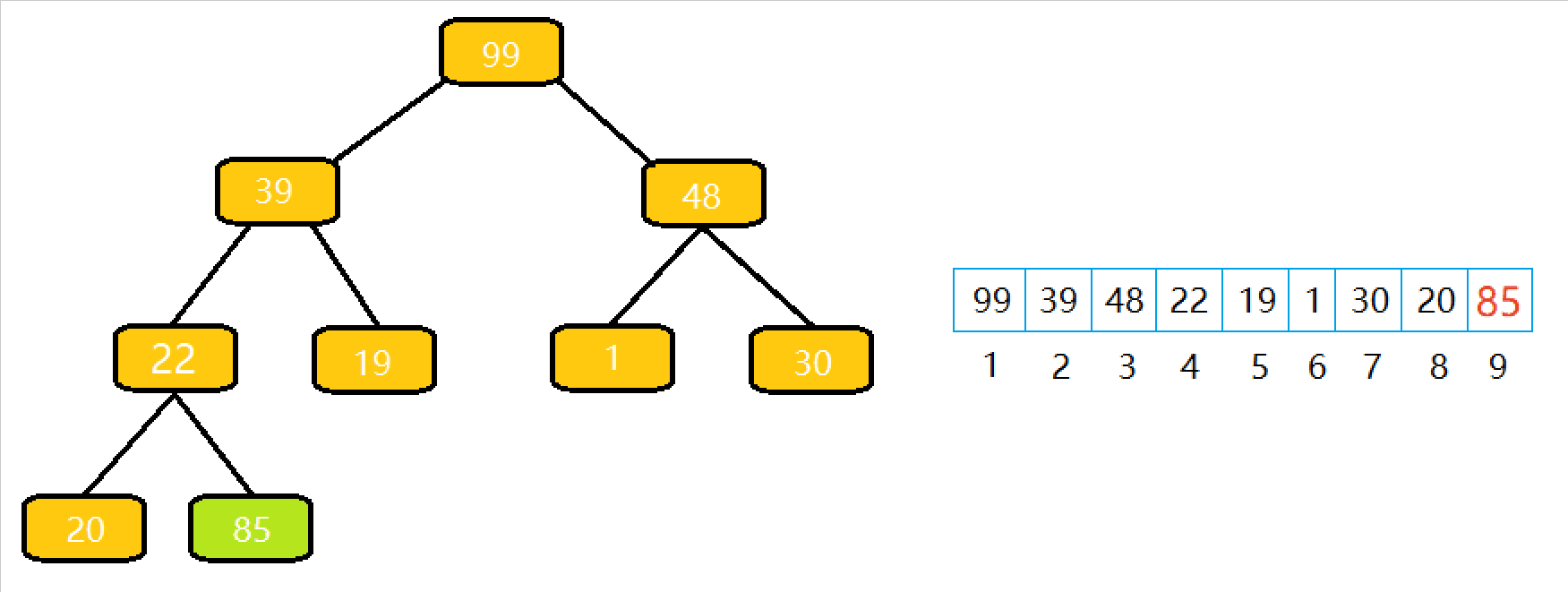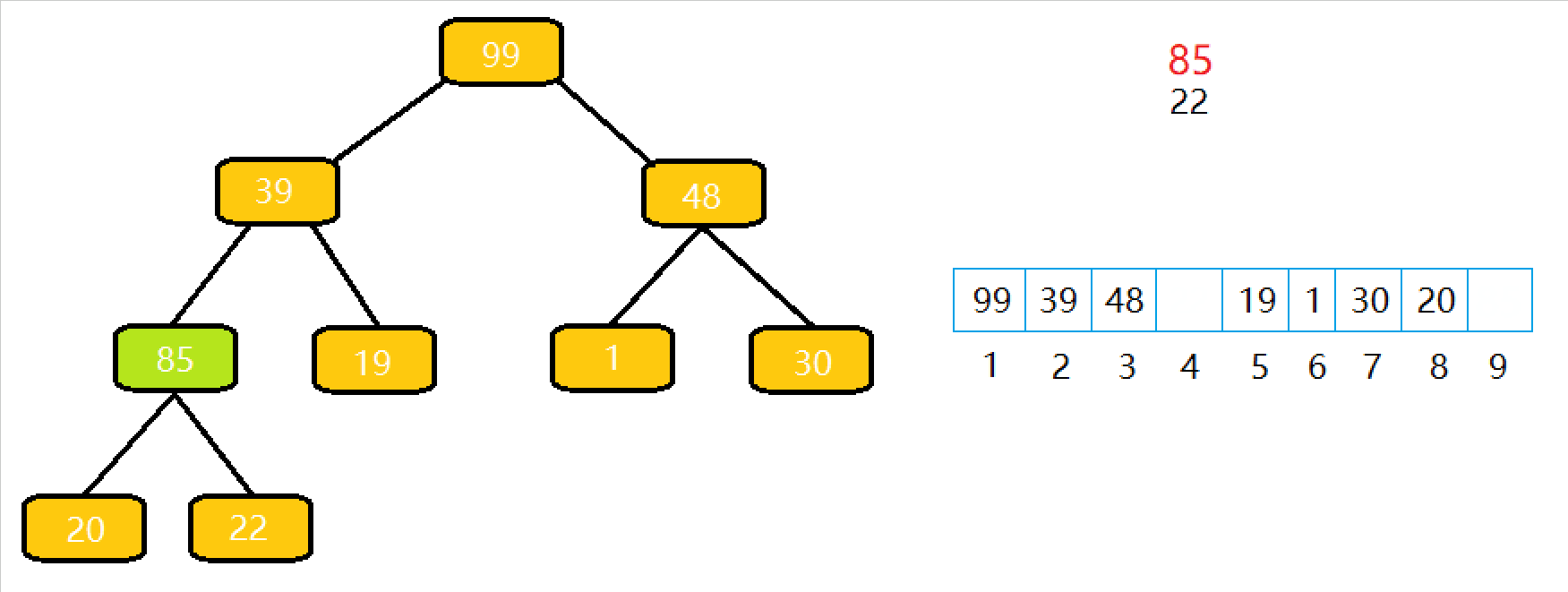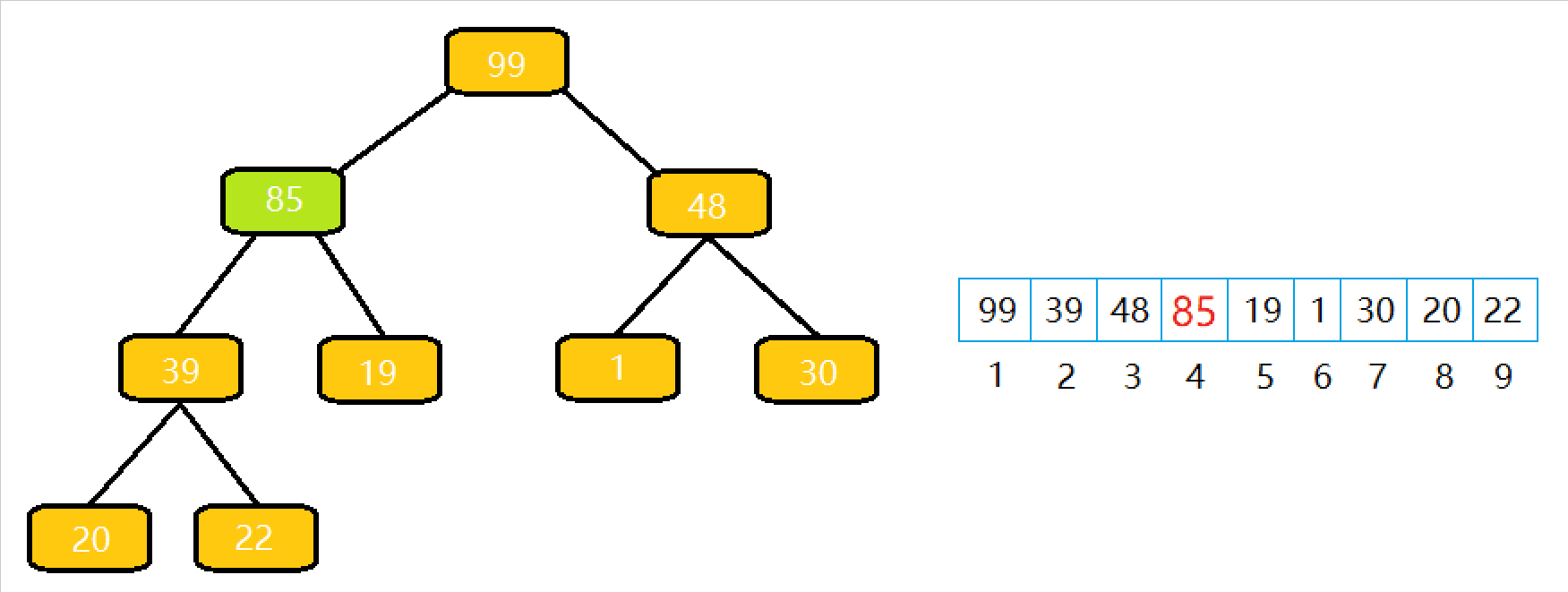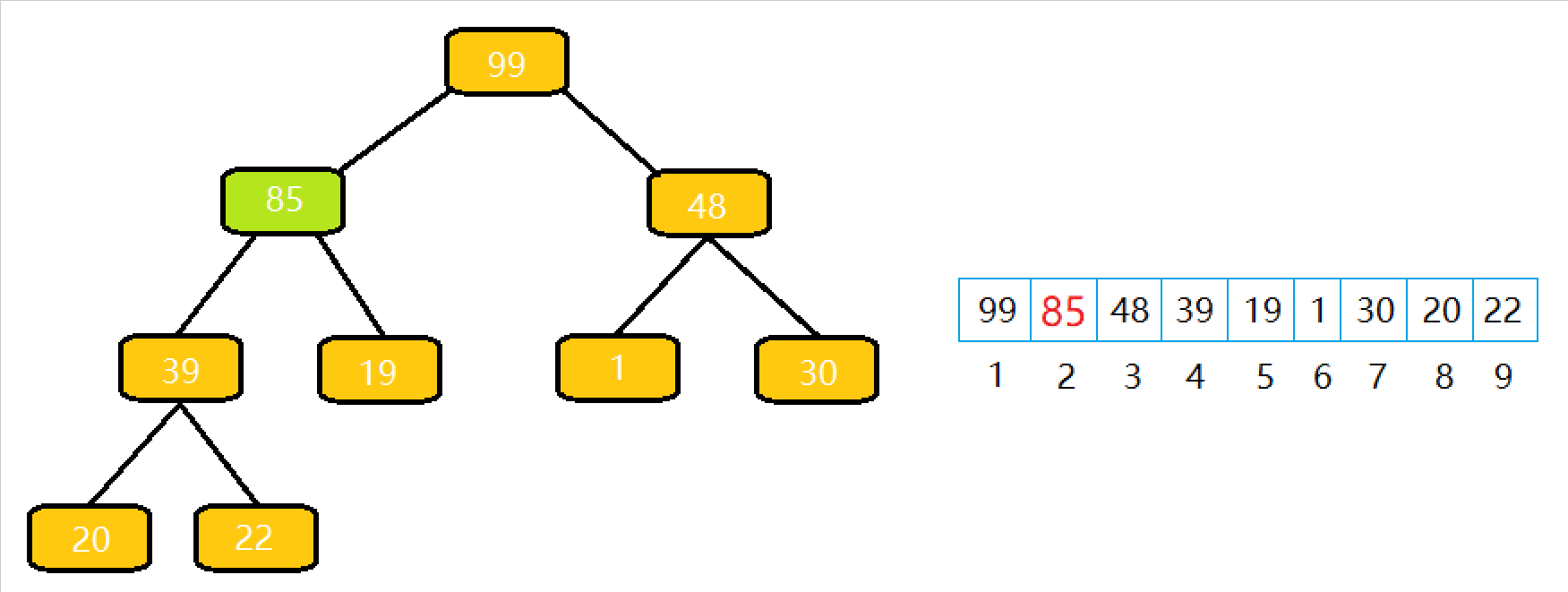
根据前两篇文章（向上调整算法以及向下调整算法），堆的实现就变得巨简单了。 

1 创建 
创建⼀个⾜够⼤的数组充当堆； 
创建⼀个变量 n，⽤来标记堆中元素的个数

const int N = 1e6 + 10;
int n;
int heap[N];

2 插⼊ 
把新来的元素放在最后⼀个位置，然后从最后⼀个位置开始执⾏⼀次向上调整算法即可。

void push(int x)
{
	heap[++n] = x;
	up(n);
}

时间复杂度： 
时间开销在向上调整算法上，时间复杂度为 O(log N) 。

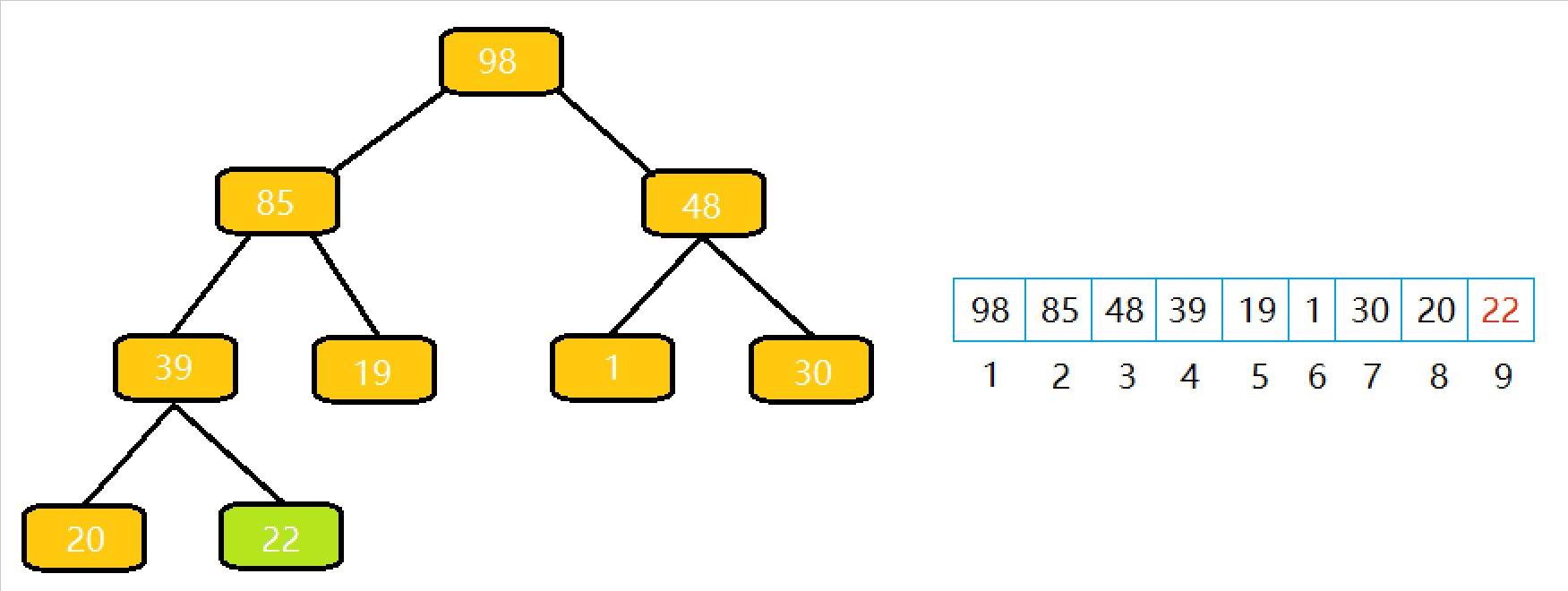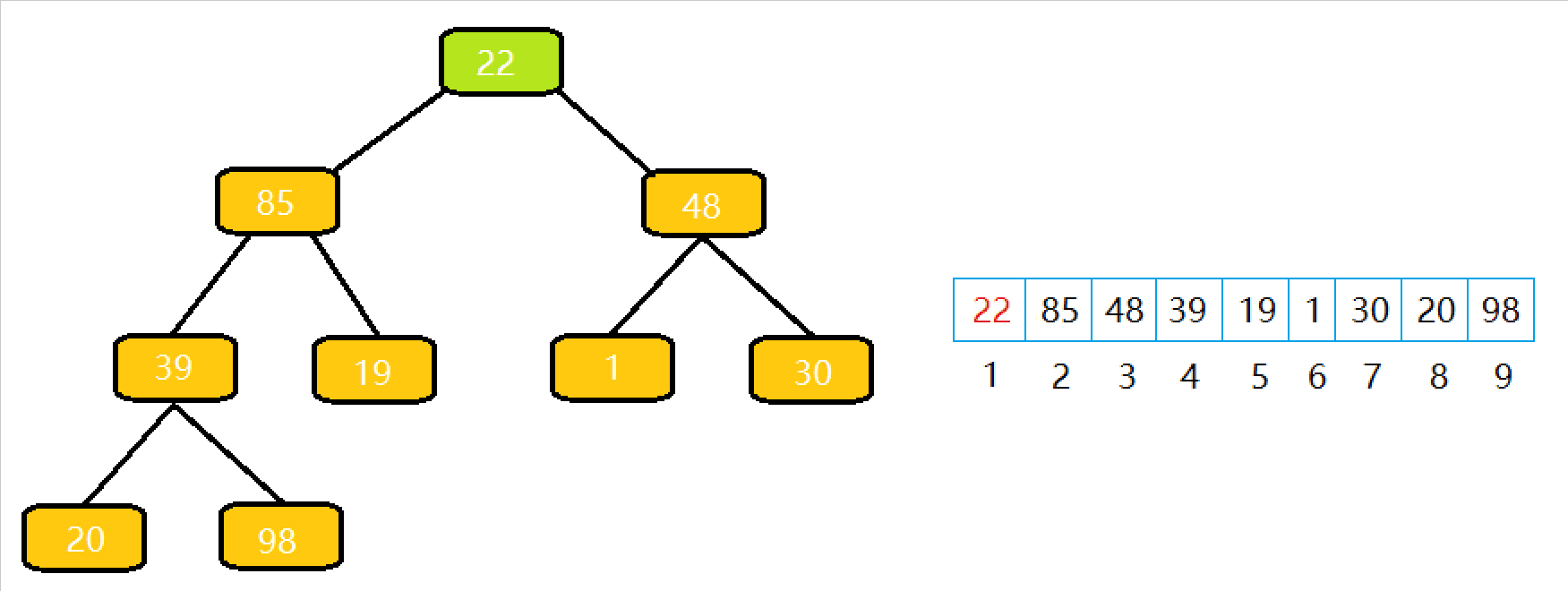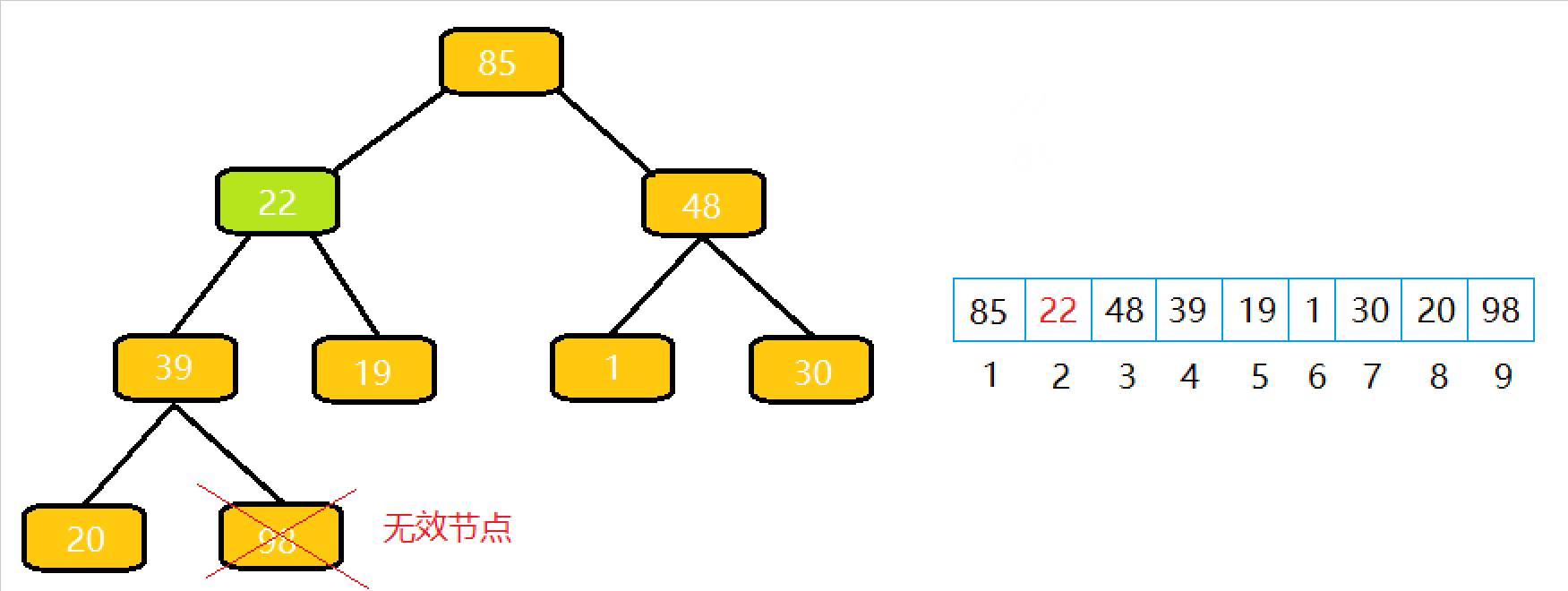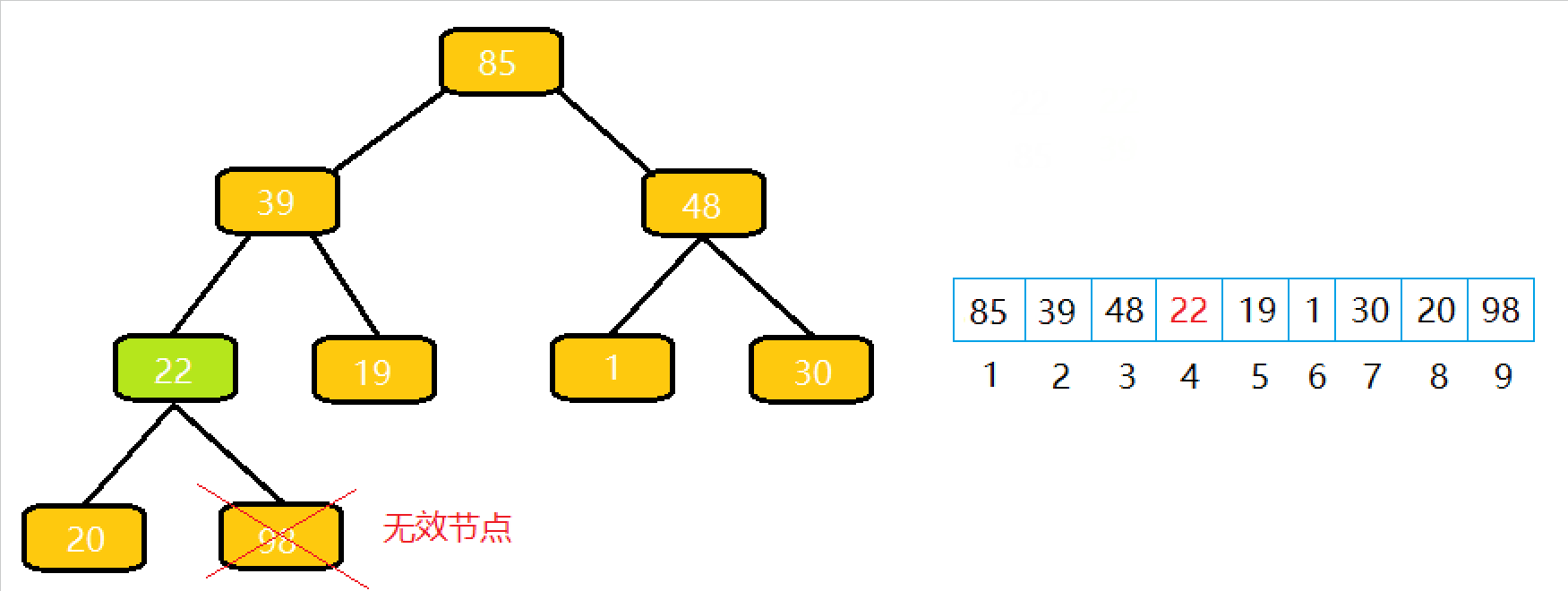
3 删除栈顶元素 
将栈顶元素和最后⼀个元素交换，然后 n--，删除最后⼀个元素； 
从根节点开始执⾏⼀次向下调整算法即可

void pop()
{
	swap(heap[1], heap[n]);
	--n;
	down(1);
}

时间复杂度： 
时间开销在向上调整算法上，时间复杂度为 O(log N) 。

4 堆顶元素 
下标为 1 位置的元素，就是堆顶元素

int top() { return heap[1]; }

时间复杂度： 
显然是 O(1) 。

5 堆的⼤⼩ 
n 的值。

int size() { return n; }

时间复杂度： 
显然是 O(1) 。

全部代码实现：

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int n;
int heap[N];

//向上调整算法
void up(int child) //每次和父亲做比较
{
	int parent = child / 2;
	//父节点存在且当前结点值大于父节点的权值
	while (parent >= 1 && heap[child] > heap[parent])
	{
		swap(heap[child], heap[parent]);
		child = parent;
		parent = child / 2;
	}
}

// 向下调整算法
void down(int parent)//拿当前结点和孩子作比较
{
	int child = parent * 2;
	//当孩子存在指向向下调整算法
	while (child <= n) //左孩子都不存在，右孩子一定不存在
	{
		//找最大的孩子
		//存在右孩子并且右孩子大于左孩子,条件满足指向最大的孩子，否则不作为
		if (child + 1 <= n && heap[child + 1] > heap[child]) child++;
		if (heap[parent] >= heap[child]) return; //如果父节点大于孩子节点就不用调整了
		
		swap(heap[parent], heap[child]); //交换父子节点
		parent = child; //父节点向下走
		child = parent * 2; //孩子向下走
	}
}

// 插入元素
void push(int x)
{
	heap[++n] = x;
	up(n);
}

// 删除堆顶元素
void pop()
{
	swap(heap[1], heap[n]);
	--n;
	down(1);
}

// 查询堆顶元素
int top() { return heap[1]; }
// 堆的大小
int size() { return n; }

int main()
{
	//测试堆
	int a[10] = { 1, 41, 23, 10, 11, 2, -1, 99, 14, 0 };

	//将这10个数依次放入堆中
	for (int i = 0; i < 10; ++i)
	{
		push(a[i]);
	}

	//输出降序
	while (size())
	{
		cout << top() << " ";
		pop();
	}

	return 0;
}

• 在大根堆中，每次拿出的堆顶元素都是最大的，删完之后再拿出的堆顶元素是次大的，所以输出的结果是一个降序的结果