实验目的
-
加深对窗函数法设计 FIR 数字滤波器的基本原理的理解。
-
学习用 Matlab 语言的窗函数法编写设计 FIR 数字滤波器的程序。
-
了解 Matlab 语言有关窗函数法设计 FIR 数字滤波器的常用函数用法。
-
掌握 FIR 滤波器的快速卷积实现原理。
-
不同滤波器的设计方法具有不同的优缺点,因此要全面、客观看待可能面对或出现的问题。
实验原理
用窗函数法设计FIR 数字滤波器
FIR数字滤波器的系统函数为
H ( z ) = ∑ n = 0 N − 1 h ( n ) z − n H(z)=\sum_{n=0}^{N-1} h(n) z^{-n} H(z)=n=0∑N−1h(n)z−n
这个公式也可以看成是离散 LSI 系统的系统函数
H ( z ) = Y ( z ) X ( z ) = b ( z ) a ( z ) = ∑ m = 0 M b m z − m 1 + ∑ k = 1 N a k z − k = b 0 + b 1 z − 1 + b 2 z − 2 + ⋯ + b m z − m 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a k z − k H(z)=\frac{Y(z)}{X(z)}=\frac{b(z)}{a(z)}=\frac{\sum_{m=0}^M b_m z^{-m}}{1+\sum_{k=1}^N a_k z^{-k}}=\frac{b_0+b_1 z^{-1}+b_2 z^{-2}+\cdots+b_m z^{-m}}{1+a_1 z^{-1}+a_2 z^{-2}+\cdots+a_k z^{-k}} H(z)=X(z)Y(z)=a(z)b(z)=1+∑k=1Nakz−k∑m=0Mbmz−m=1+a1z−1+a2z−2+⋯+akz−kb0+b1z−1+b2z−2+⋯+bmz−m
分母 a 0 a_0 a0 为 1, 其余 a k a_k ak 全都为 0时的一个特例。由于极点全部集中在零点, 稳定和线性相位特性是 FIR滤波器的突出优点, 因此在实际中广泛使用。
FIR 滤波器的设计任务是选择有限长度的 h ( n ) h(n) h(n), 使传输函数 H ( e j ω ) H\left(e^{j\omega}\right) H(ejω)满足技术要求。主要设计方法有窗函数法、频率采样法和切比雪夫等波纹逼近法等。本实验主要介绍窗函数法。
用窗函数法设计 FIR 数字滤波器的基本步骤如下:
(1) 根据过渡带和阻带衰减指标选择窗函数的类型, 估算滤波器的阶数 N N N。
(2) 由数字滤波器的理想频率响应 H ( e j ω ) H\left(e^{j\omega}\right) H(ejω)求出其单位冲激响应 h d ( n ) h_{d}(n) hd(n)。 可用自定义函数 ideal_lp \text{ideal\_lp} ideal_lp实现理想数字低通滤波器频率响应的求解。程序清单如下:
function hd = ideal_lp(wc, N) % 点 0 到 N-1 之间的理想脉冲响应
% wc = 截止频率 (弧度)
% N = 理想滤波器的长度
tao = (N-1)/2;
n = [0:(N-1)];
m = n - tao + eps; % 加一个小数以避免 0 作除数
hd = sin(wc * m) ./ (pi * m);
end
其它选频滤波器可以由低通频响特性合成。如一个通带在 ω c 1 ∼ ω c 2 \omega_{c1} \sim \omega_{c2} ωc1∼ωc2 之间的带通滤波器在给定 N N N值的条件下,可以用下列程序实现:
Hd = ideal_lp(wc2, N) - ideal_lp(wc1, N);
(3) 计算数字滤波器的单位冲激响应 h ( n ) = w ( n ) h d ( n ) h(n) = w(n)hd(n) h(n)=w(n)hd(n)。
(4) 检查设计的滤波器是否满足技术指标。
如果设计的滤波器不满足技术指标,则需要重新选择或调整窗函数的类型,估算滤波器的阶数 N N N。再重复前面的四个步骤,直到满足指标。
常用的窗函数有矩形窗、三角形窗、汉宁窗、哈明窗、切比雪夫窗、布莱克曼窗、凯塞窗等,Matlab均有相应的函数可以调用。另外,MATLAB 信号处理工具箱还提供了 'firl’函数,可以用于窗函数法设计 FIR 滤波器。
由于第一类线性相位滤波器 (类型 I)能进行低通、高通、带通、带阻滤波器的设计,因此,本实验所有滤波器均采用第一类线性相位滤波器。
各种窗函数特性的比较
| 窗函数 | 旁瓣峰值/dB | 近似过渡带宽 | 精确过渡带宽 | 阻带最小衰减/dB |
|---|---|---|---|---|
| 矩形窗 | -13 | 4 π / N 4\pi/N 4π/N | 1.8 π / N 1.8\pi/N 1.8π/N | 21 |
| 三角形窗 | -25 | 8 π / N 8\pi/N 8π/N | 6.1 π / N 6.1\pi/N 6.1π/N | 25 |
| 汉宁窗 | -31 | 8 π / N 8\pi/N 8π/N | 6.2 π / N 6.2\pi/N 6.2π/N | 44 |
| 哈明窗 | -41 | 8 π / N 8\pi/N 8π/N | 6.6 π / N 6.6\pi/N 6.6π/N | 53 |
| 布莱克曼窗 | -57 | 12 π / N 12\pi/N 12π/N | 11 π / N 11\pi/N 11π/N | 74 |
| 凯塞窗 | -57 | 无 | 10 π / N 10\pi/N 10π/N | 80 |
信号的整数倍零值内插
设 x ( n ) x(n) x(n) 是连续信号 x a ( t ) x_a(t) xa(t) 的采样序列,其采样频率为 f 1 = 1 T 1 ( Hz ) , T 1 f_1 = \frac{1}{T_1} (\text{Hz}), T_1 f1=T11(Hz),T1是采样间隔。如果将其采样频率降低到原来的 1 D \frac{1}{D} D1( D D D 为大于 1的整数,称为抽取因子),最简单的方法是对 x ( n ) x(n) x(n) 每 D − 1 D-1 D−1 个点抽取 1点,组成一个新的序列 y ( n ) y(n) y(n)。由于 y ( n ) y(n) y(n) 的采样间隔 T 2 = D T 1 T_2 = DT_1 T2=DT1,除非抽取后仍能满足采样定理,否则会引起频谱混叠现象。信号抽取前后的频谱关系见教材第8 章的 8.2节。为了避免抽取后的频率混叠,在抽取前先采用一个抗混叠低通滤波器对信号滤波,把信号的频带限制在某个频率以下。
抗混叠滤波器的系统函数为:
H ( e j ω ) = { 1 ∣ ω ∣ < π D 0 π D ≤ ∣ ω ∣ ≤ π H(e^{j\omega}) = \begin{cases} 1 & |\omega| < \frac{\pi}{D} \\ 0 & \frac{\pi}{D} \leq |\omega| \leq \pi \end{cases} H(ejω)={10∣ω∣<DπDπ≤∣ω∣≤π
例题
例2-2 选择合适的窗函数设计一个FIR 数字低通滤波器
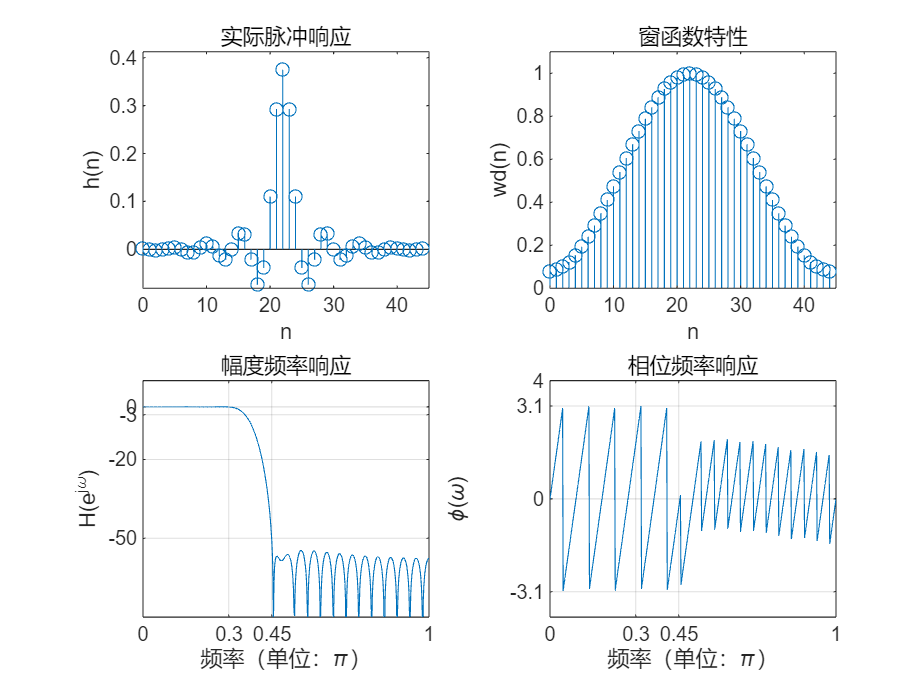
要求:通带截止频率为ωp=0.3 π ,Rp=0.05dB;阻带截止频率为ωs=0.45 π ,As=50dB。描绘该滤波器的脉冲响应、窗函数及滤波器的幅频响应曲线和相频响应曲线。分析:根据设计指标要求,并查表2-1,选择哈明窗。程序清单如下:
addpath('.\2024-2025(1)《信号处理实验》资料(请拷贝到u盘中,每次试验带到实验室)\实验中用到的一些函数和音频图像文件');
wp = 0.3*pi;
ws = 0.45*pi;
deltaw = ws - wp;
N0 = ceil(6.6*pi/deltaw);
N = N0 + mod(N0 + 1, 2); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = (hamming(N))';
wc = (ws + wp) / 2;
hd = ideal_lp(wc, N);
b = hd .* windows;
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20 * log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2 * pi / 1000;
Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
subplot(2, 2, 1);
stem(n, b);
axis([0, N, 1.1 * min(b), 1.1 * max(b)]);
title('实际脉冲响应');
xlabel('n');
ylabel('h(n)');
subplot(2, 2, 2);
stem(n, windows);
axis([0, N, 0, 1.1]);
title('窗函数特性');
xlabel('n');
ylabel('wd(n)');
subplot(2, 2, 3);
plot(w/pi, db);
axis([0, 1, -80, 10]);
title('幅度频率响应');
xlabel('频率(单位:\pi)');
ylabel('H(e^{j\omega})');
set(gca, 'XTickMode', 'manual', 'XTick', [0, wp/pi, ws/pi, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-50, -20, -3, 0]);
grid on;
subplot(2, 2, 4);
plot(w/pi, pha);
axis([0, 1, -4, 4]);
title('相位频率响应');
xlabel('频率(单位:\pi)');
ylabel('\phi(\omega)');
set(gca, 'XTickMode', 'manual', 'XTick', [0, wp/pi, ws/pi, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-3.1416, 0, 3.1416, 4]);
grid on;
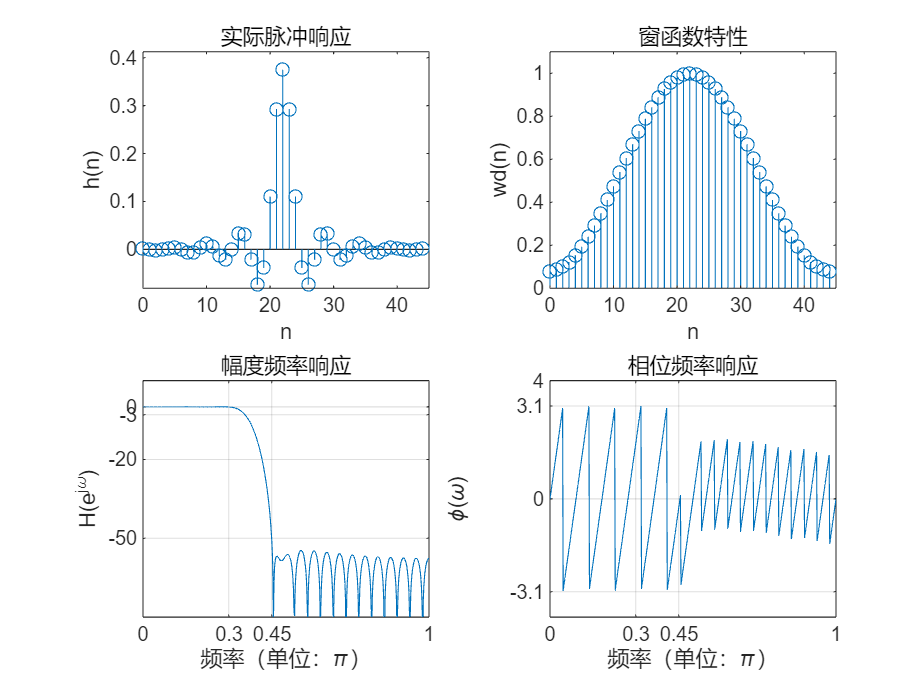
例2-3 用Matlab 信号处理工具箱的fir1 函数设计一个FIR 数字低通滤波器
要求:通带截止频率为ωp=0.3 π ,Rp=0.05dB;阻带截止频率为ωs=0.45 π ,As=50dB。
close;clear;
wp = 0.3*pi;
ws = 0.45*pi;
deltaw = ws - wp;
N0 = ceil(6.6*pi/deltaw);
N = N0 + mod(N0 + 1, 2); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = hamming(N); % 使用哈明窗,此句可省略
wc = (ws + wp) / 2 / pi; % 截止频率取归一化通阻带频率的平均值
b = fir1(N-1, wc, windows); % 用 fir1 函数求系统函数系数,windows 可省略
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2*pi/1000;
Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
draw(n,b,N,windows,w,db,wp,ws,pha,As);
实验内容
1、阅读并输入实验原理中介绍的例题程序,观察输出的数据和图形,结合基本原理理解每一条语句的含义。
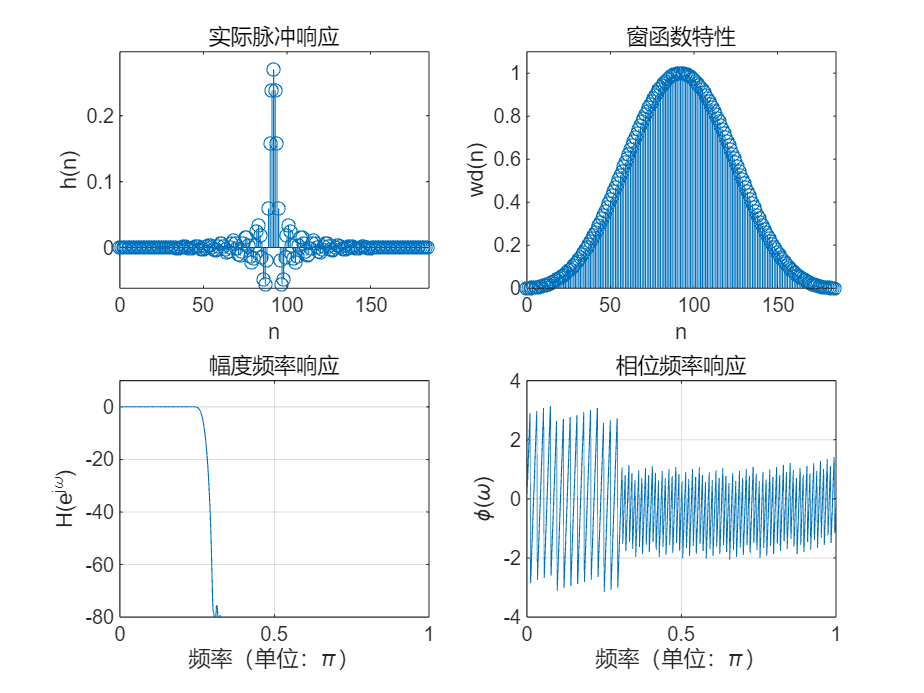
2、选择合适的窗函数设计FIR 数字低通滤波器
要求:ωp=0.24 π ,Rp=0.1dB;ωs=0.3 π ,As=60dB。描绘该滤波器的脉冲响应、窗函数及滤波器的幅频响应曲线和相频响应曲线。
close;clear;
As=60;
wp = 0.24*pi;
ws = 0.3*pi;
deltaw = ws - wp;
N0 = ceil(11*pi/deltaw);
N = N0 + mod(N0 + 1, 2); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = blackman(N); % 使用布莱克曼窗
wc = (ws + wp) / 2 / pi; % 截止频率取归一化通阻带频率的平均值
b = fir1(N-1, wc, windows); % 用 fir1 函数求系统函数系数,windows 可省略
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2*pi/1000;
% Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
% As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
draw(n,b,N,windows,w,db,wp,ws,pha,As);
3、调用信号产生函数xtg 产生具有加性噪声的信号x(t),并显示信号及其频谱。
addpath('.\2024-2025(1)《信号处理实验》资料(请拷贝到u盘中,每次试验带到实验室)\实验中用到的一些函数和音频图像文件');
[xt,tf]=xtg(1000);
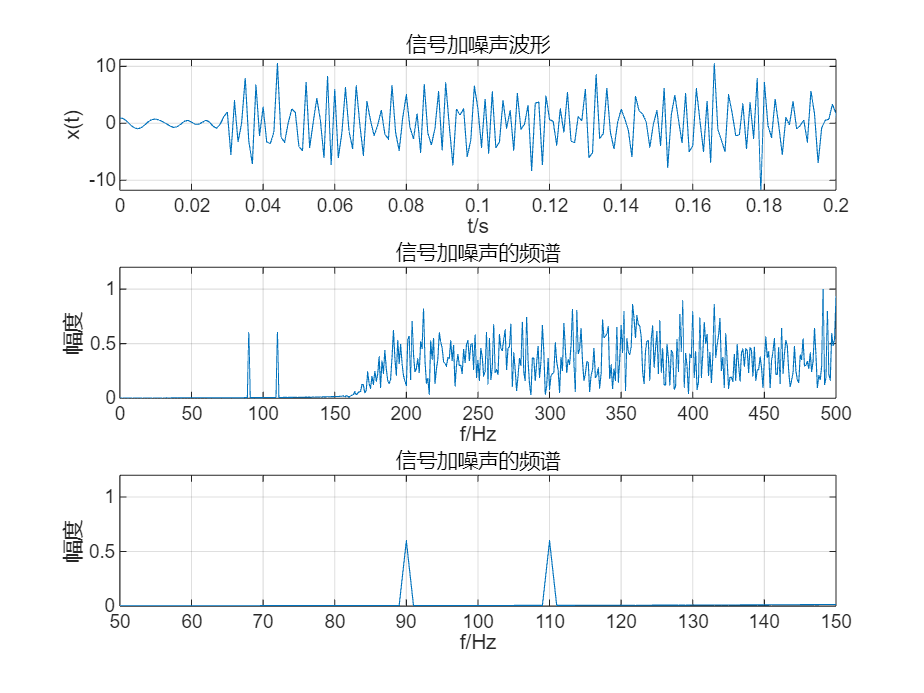
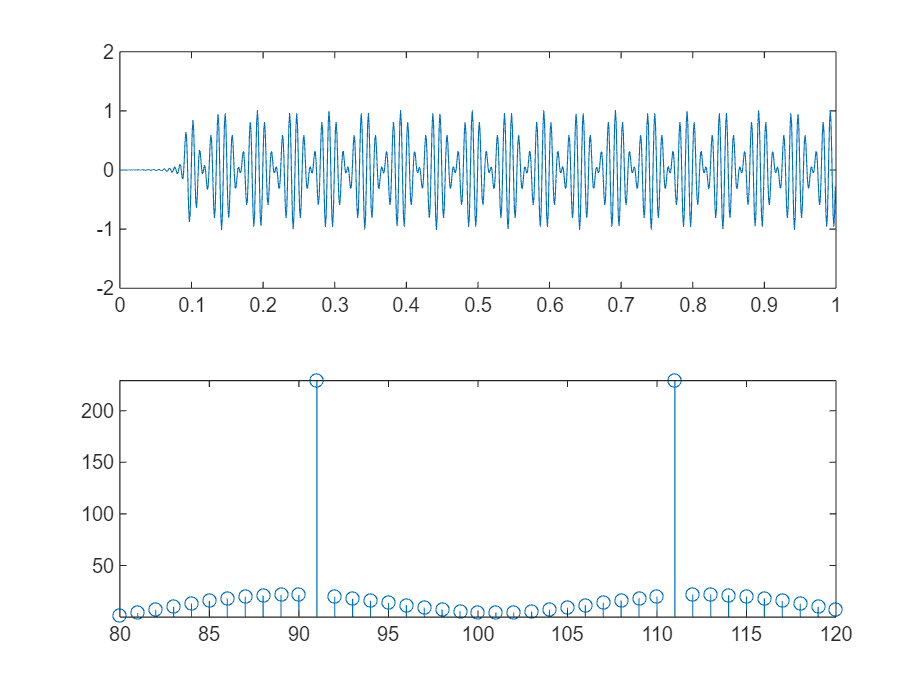
4、采用实验内容步骤2 中设计的FIR 数字低通滤波器
调用Matlab 快速卷积函数fftfilt 实现对x(t)的滤波,从高频噪声中提取x(t)中的单频调幅信号。绘图显示滤波器的频率响应特性曲线、滤波器输出信号的幅频特性图和时域波形图。
yt = fftfilt(b, xt);
Hyk = abs(fft(yt));
figure;
subplot(2, 1, 1);
plot(tf, yt);
axis([0, 1, -2, 2]);
subplot(2, 1, 2);
stem(Hyk);
axis([80, 120, min(Hyk), max(Hyk)]);
5、 选做题 ,读取音频信号 motherland.wav,得到 xn
1 对 xn进行 I=2的整数倍 0值内插,得到音频信号 yn1
2 设计一个 镜像 低通滤波器(可在实验内容 2的代码上进行修改)
3 对 yn1进行 滤波,得到音频信号 yn2。
①音频播放: 依次播放 原音频 信号 xn、 yn1和 yn2,体验 整数倍 0值内插后的 音质。
close;clear;
[xn,fs]=audioread('motherland.wav');% 读取音频信号
% sound(xn,fs); % 播放音频信号,
% pause(length(xn)/fs); % 暂停执行程序 length(xn)/fs秒,确保音频播 放完。
I=2; % 实现 I=2的整数倍 0值内插
for i=1:length(xn);
yn1(I*i-1)=xn(i);
yn1(I*i)= 0;
end
% sound(yn1,I*fs); %采样频率变大了,为 I*fs
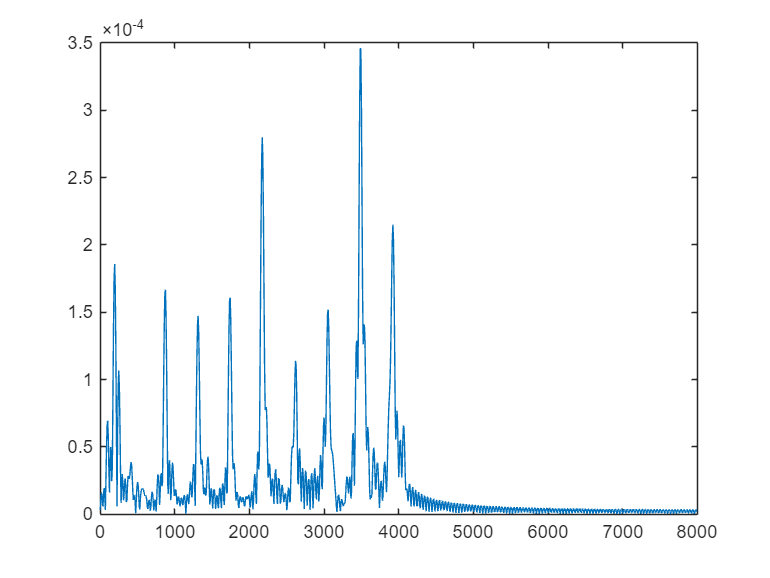
②取原音频某段信号,如 n=8000~8199 。画出该段信号模拟域幅度谱(横坐标为 f Hz );画出该段信号 I=2 内插后的模拟域幅度谱;画出该段信号内插后再经过镜像滤波后的模拟域幅度谱。
addpath('.\2024-2025(1)《信号处理实验》资料(请拷贝到u盘中,每次试验带到实验室)\实验中用到的一些函数和音频图像文件');
wp = 0.48*pi;
ws = 0.52*pi;
deltaw = ws - wp;
N0 = ceil(6.6*pi/deltaw);
N = N0 + mod(N0 + 1, 2); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = (hamming(N))';
wc = (ws + wp) / 2;
hd = ideal_lp(wc, N);
b = hd .* windows;
b
b = 1x165
0.0000 0.0003 -0.0000 -0.0003 0.0000 0.0004 -0.0000 -0.0004 0.0000 0.0005 -0.0000 -0.0005 0.0000 0.0006 0.0000 -0.0007 0.0000 0.0009 -0.0000 -0.0010 0.0000 0.0012 -0.0000 -0.0013 -0.0000 0.0015 -0.0000 -0.0018 0.0000 0.0020 0.0000 -0.0023 -0.0000 0.0026 -0.0000 -0.0029 0.0000 0.0033 -0.0000 -0.0037 -0.0000 0.0042 -0.0000 -0.0047 0.0000 0.0052 -0.0000 -0.0059 -0.0000 0.0065
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20 * log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2 * pi / 1000;
N=2048;
Xn=1/fs*fft(xn(8000:8199),N); % 从 xn中取 200点做谱分析, N可取 2048
plot((0:N/2-1)*fs/N,abs(Xn(1:N/2)));% 模拟域幅度谱
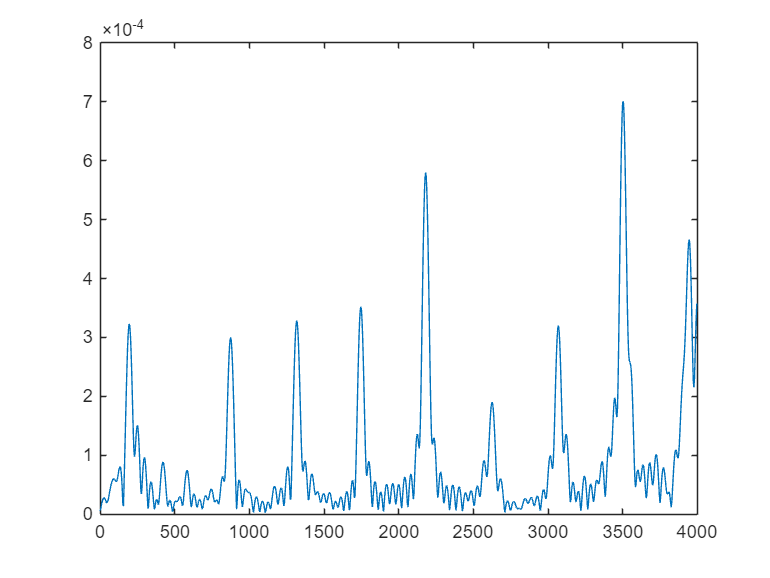
Yn1=1/(I*fs)*fft(yn1(16000:16399),N); % 内插后,200点长变成了400点长
plot((0:N/2-1)*I*fs/N,abs(Yn1(1:N/2)));
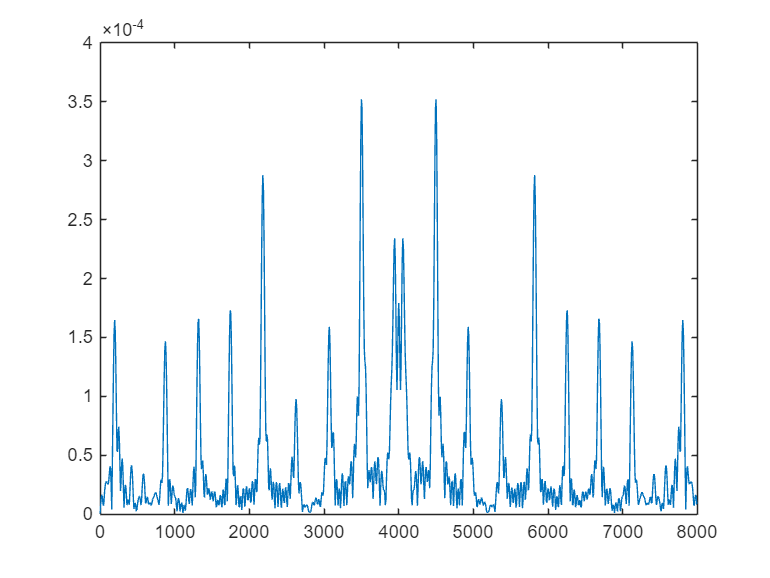
yn2=filter(b,1,yn1); % 对yn1进行滤波,b为所设计的镜像滤波器
Yn2=1/(I*fs)*fft(yn2(16000:16399),N); % 内插后,200点长变成了400点长
plot((0:N/2-1)*I*fs/N,abs(Yn2(1:N/2)));
思考题
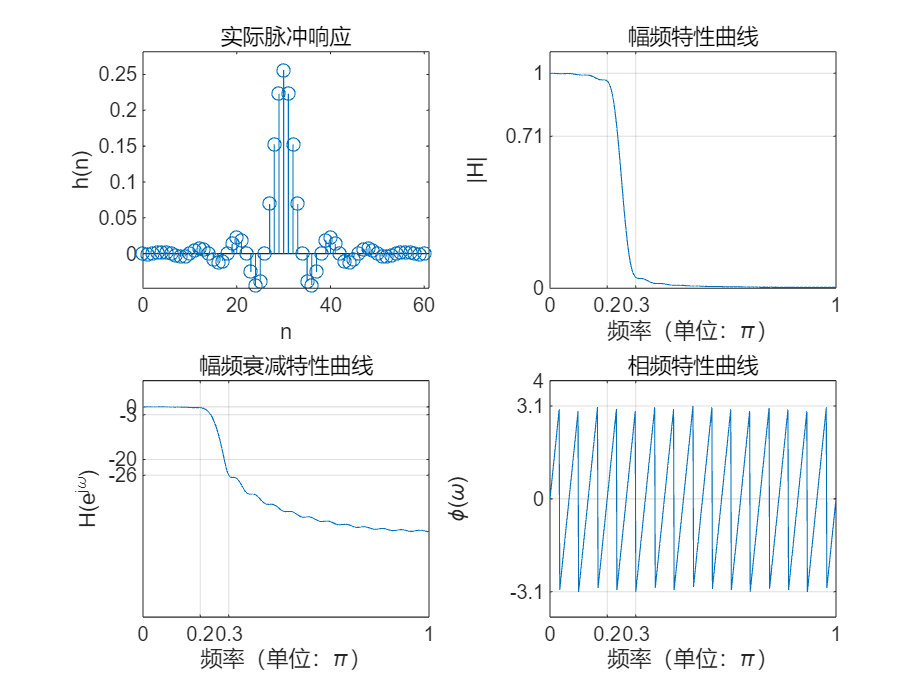
根据下面指标要求设计四种不同类型的FIR 线性相位数字滤波器,要求画出h(n),幅频特性曲线、幅频衰减特性曲线,相频特性曲线,标注相关信息,包括横坐标,纵坐标的单位,曲线名称。
close;clear;
wp = 0.2*pi;
ws = 0.3*pi;
deltaw = ws - wp;
N0 = ceil(6.1*pi/deltaw);
N = N0 + mod(N0 + 1, 2); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = triang(N); % 使用哈明窗,此句可省略
wc = (ws + wp) / 2 / pi; % 截止频率取归一化通阻带频率的平均值
b = fir1(N-1, wc, windows); % 用 fir1 函数求系统函数系数,windows 可省略
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2*pi/1000;
Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
draw2(n,b,N,w,db,wp,ws,mag,pha,As);
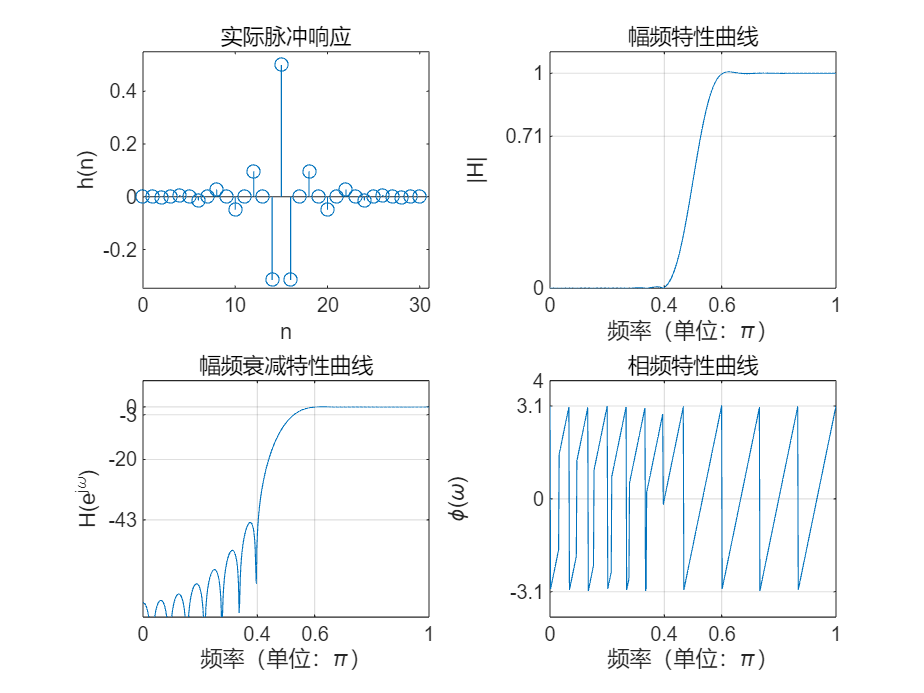
close;clear;
wp = 0.6*pi;
ws = 0.4*pi;
deltaw = wp - ws;
N0 = ceil(6.2*pi/deltaw);
N = N0 + mod(N0 + 1, 2); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = hanning(N); % 使用哈明窗,此句可省略
wc = (ws + wp) / 2 / pi; % 截止频率取归一化通阻带频率的平均值
b = fir1(N-1, wc,'high', windows); % 用 fir1 函数求系统函数系数,windows 可省略
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2*pi/1000;
Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
% As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
As=43;
draw2(n,b,N,w,db,wp,ws,mag,pha,As);
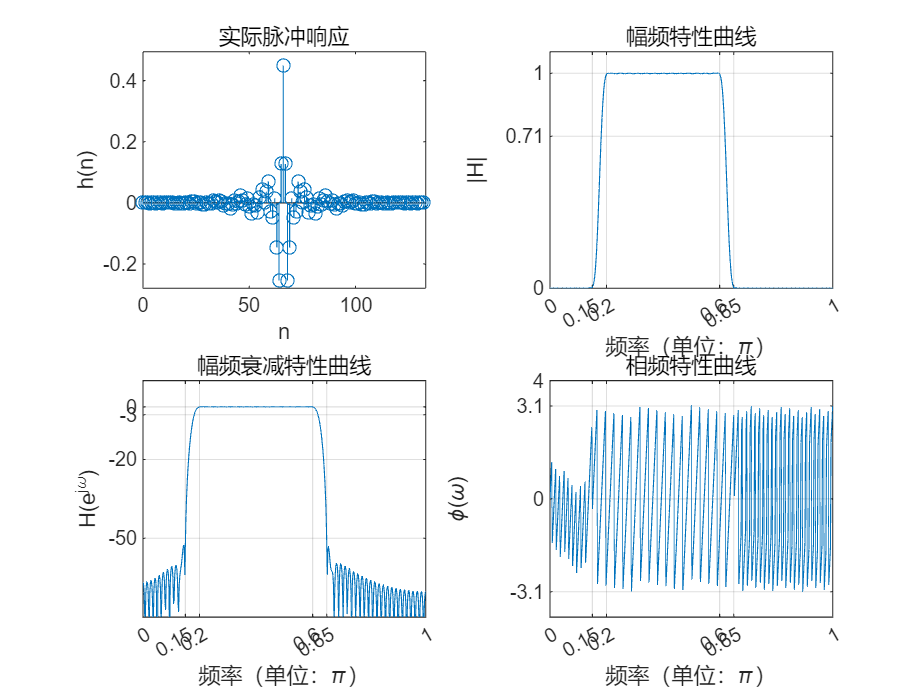
close;clear;
wp = [0.2,0.6]*pi;
ws = [0.15,0.65]*pi;
deltaw = wp - ws;
N0 = ceil(6.6*pi./deltaw);
N = max(N0 + mod(N0 + 1, 2)); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = hamming(N); % 使用哈明窗,此句可省略
wc = (ws + wp) / 2 / pi; % 截止频率取归一化通阻带频率的平均值
b = fir1(N-1, wc,'bandpass'); % 用 fir1 函数求系统函数系数,windows 可省略
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps) / max(mag));
pha = angle(H);
nextfigure
n = 0:N-1;
dw = 2*pi/1000;
Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
% As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
As=50;
draw3(n,b,N,w,db,wp,ws,mag,pha,As);

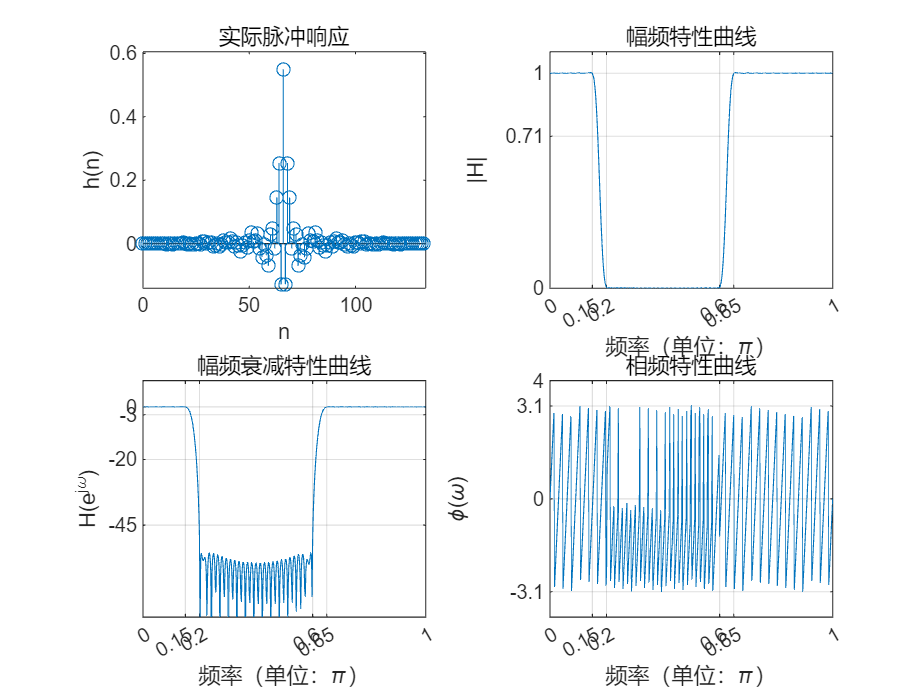
close;clear;
wp = [0.2,0.6]*pi;
ws = [0.15,0.65]*pi;
deltaw = wp - ws;
N0 = ceil(6.6*pi./deltaw);
N = max(N0 + mod(N0 + 1, 2)); % 为实现 FIR 类型 1 偶对称滤波器,应确保 N 为奇数
windows = hamming(N); % 使用哈明窗,此句可省略
wc = (ws + wp) / 2 / pi; % 截止频率取归一化通阻带频率的平均值
b = fir1(N-1, wc,'stop'); % 用 fir1 函数求系统函数系数,windows 可省略
[H, w] = freqz(b, 1, 1000, 'whole');
H = (H(1:501))';
w = (w(1:501))';
mag = abs(H);
db = 20*log10((mag + eps) / max(mag));
pha = angle(H);
n = 0:N-1;
dw = 2*pi/1000;
Rp = -(min(db(1:wp/dw + 1))); % 检验通带波动
% As = -round(max(db(ws/dw + 1:501))); % 检验最小阻带衰减
As=45;
draw3(n,b,N,w,db,wp,ws,mag,pha,As);
绘图函数
用到的绘图函数,可以以.m文件保存,放在同一路径下。或addpath加入函数的绝对/相对路径。
% function draw(n,b,N,windows,w,db,wp,ws,pha,As)
% subplot(2, 2, 1);
% stem(n, b);
% axis([0, N, 1.1 * min(b), 1.1 * max(b)]);
% title('实际脉冲响应');
% xlabel('n');
% ylabel('h(n)');
%
% subplot(2, 2, 2);
% stem(n, windows);
% axis([0, N, 0, 1.1]);
% title('窗函数特性');
% xlabel('n');
% ylabel('wd(n)');
%
% subplot(2, 2, 3);
% plot(w/pi, db);
% axis([0, 1, -80, 10]);
% title('幅度频率响应');
% xlabel('频率(单位:\pi)');
% ylabel('H(e^{j\omega})');
% set(gca, 'XTickMode', 'manual', 'XTick', [0, wp/pi, ws/pi, 1]);
% set(gca, 'YTickMode', 'manual', 'YTick', [-As, -20, -3, 0]);
% grid on;
%
% subplot(2, 2, 4);
% plot(w/pi, pha);
% axis([0, 1, -4, 4]);
% title('相位频率响应');
% xlabel('频率(单位:\pi)');
% ylabel('\phi(\omega)');
%
% set(gca, 'XTickMode', 'manual', 'XTick', [0, wp/pi, ws/pi, 1]);
% set(gca, 'YTickMode', 'manual', 'YTick', [-3.1416, 0, 3.1416, 4]);
% grid on;
% function draw2(n,b,N,w,db,wp,ws,mag,pha,As)
% subplot(2, 2, 1);
% stem(n, b);
% axis([0, N, 1.1 * min(b), 1.1 * max(b)]);
% title('实际脉冲响应');
% xlabel('n');
% ylabel('h(n)');
%
% subplot(2, 2, 2);
% plot(w/pi, mag);
% xlabel('频率(单位:\pi)');
% ylabel('|H|');
% title('幅频特性曲线');
% axis([0, 1, 0, 1.1]);
% set(gca, 'XTickMode', 'manual', 'XTick', [0, min([wp/pi,ws/pi]), max([wp/pi,ws/pi]), 1]);
% set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]);
% grid on;
%
% subplot(2, 2, 3);
% plot(w/pi, db);
% axis([0, 1, -80, 10]);
% title('幅频衰减特性曲线');
% xlabel('频率(单位:\pi)');
% ylabel('H(e^{j\omega})');
% set(gca, 'XTickMode', 'manual', 'XTick', [0, min([wp/pi,ws/pi]), max([wp/pi,ws/pi]), 1]);
% set(gca, 'YTickMode', 'manual', 'YTick', [min([-As,-20]), max([-As,-20]), -3, 0]);
% grid on;
%
% subplot(2, 2, 4);
% plot(w/pi, pha);
% axis([0, 1, -4, 4]);
% title('相频特性曲线');
% xlabel('频率(单位:\pi)');
% ylabel('\phi(\omega)');
%
% set(gca, 'XTickMode', 'manual', 'XTick', [0, min([wp/pi,ws/pi]), max([wp/pi,ws/pi]), 1]);
% set(gca, 'YTickMode', 'manual', 'YTick', [-3.1416, 0, 3.1416, 4]);
% grid on;
% function draw3(n,b,N,w,db,wp,ws,mag,pha,As)
% unique_ticks = unique([0, wp/pi, ws/pi, 1]);
% subplot(2, 2, 1);
% stem(n, b);
% axis([0, N, 1.1 * min(b), 1.1 * max(b)]);
% title('实际脉冲响应');
% xlabel('n');
% ylabel('h(n)');
%
% subplot(2, 2, 2);
% plot(w/pi, mag);
% xlabel('频率(单位:\pi)');
% ylabel('|H|');
% title('幅频特性曲线');
% axis([0, 1, 0, 1.1]);
% set(gca, 'XTickMode', 'manual', 'XTick', unique_ticks);
% set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]);
% grid on;
%
% subplot(2, 2, 3);
% plot(w/pi, db);
% axis([0, 1, -80, 10]);
% title('幅频衰减特性曲线');
% xlabel('频率(单位:\pi)');
% ylabel('H(e^{j\omega})');
% set(gca, 'XTickMode', 'manual', 'XTick', unique_ticks);
% set(gca, 'YTickMode', 'manual', 'YTick', [min([-As,-20]), max([-As,-20]), -3, 0]);
% grid on;
%
% subplot(2, 2, 4);
% plot(w/pi, pha);
% axis([0, 1, -4, 4]);
% title('相频特性曲线');
% xlabel('频率(单位:\pi)');
% ylabel('\phi(\omega)');
%
% set(gca, 'XTickMode', 'manual', 'XTick', unique_ticks);
% set(gca, 'YTickMode', 'manual', 'YTick', [-3.1416, 0, 3.1416, 4]);
% grid on;


