这篇文章是对 【0-1背包】和【完全背包】问题基础的一个解答,详细讲解了【0-1背包】和【完全背包】问题的理论基础,为后面由【0-1背包】和【完全背包】问题演变而来的问题做一个铺垫,这样就不会没有思路和无从下笔了。
一、【0-1背包】问题
有N件物品和一个最大容量为W的背包,第i件物品的重量为weight[i],价值为value[i],每件物品这只能使用一次,求解将哪些物品装入背包后物品的价值的总和最大?
输入样例:weight[3,4,6,8 ] value[ 8,9,11,12 ] W=13;
解法一:回溯算法(俗称暴力求解)
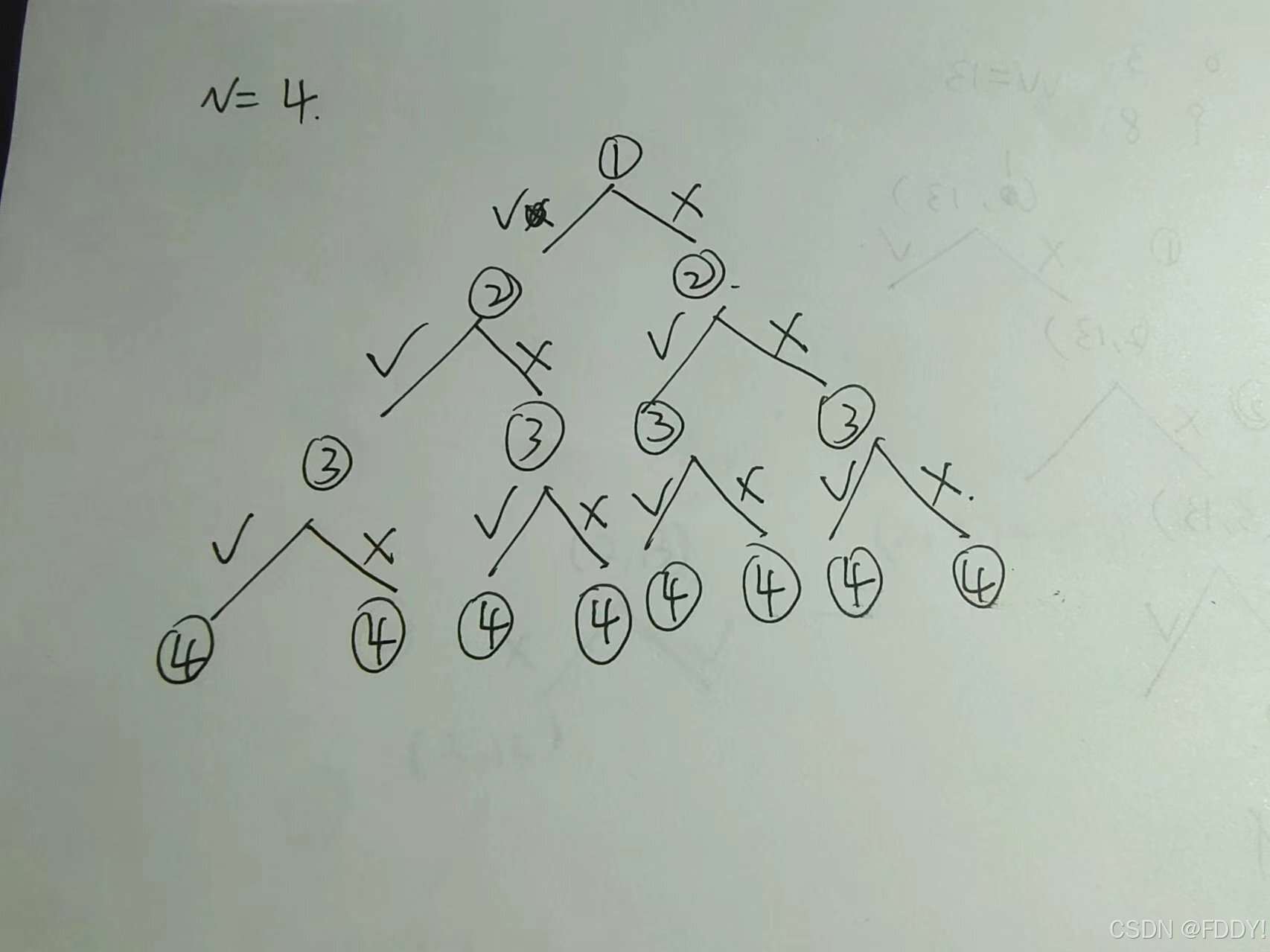
分析:每一件物品其实只有两种状态——取或者不取,所以可以使用回溯算法搜索所有的情况,时间复杂度为O(2的n次方),n表示物品的数量。(以下是我随便画的一张解空间树配合代码可以更好理解)。
#include <iostream>
using namespace std;
#include <vector>
int m = 13;
vector<int> result;
void backtrack(vector<int>& w, vector<int>& v, int sumV, int sumW, int startIndex)
{
if (sumW > m)
return;
if (sumW == m)
{
result.push_back(sumV);
return;
}
for (int i = startIndex; i < w.size(); i++)
{
sumW += w[i];
sumV += v[i];
if (sumW > m)
continue;
backtrack(w, v, sumV, sumW, i + 1);
sumW -= w[i];
sumV -= v[i];
}
}
int main()
{
vector<int> w{ 3,4,6,8 };
vector<int> v{ 8,9,11,12 };
backtrack(w, v, 0, 0, 0);
int ans = *max_element(result.begin(), result.end());
cout << ans;
}
结语:回溯算法其实是有模板的,我们在做回溯算法题的时候可以套用模板(本文章主要讲解动态规划算法,这里不多讲解回溯算法)。
解法二:动态规划
原因:暴力解法的时间复杂度是指数级别的,所以我们需要使用动态规划来优化。
二维dp解法
(1)、确定dp数组及其下标的含义:dp[i][j]:表示从下标为[0-i]的物品中取任意物品并放进容量为j的背包的价值总和。
(2)、确定递推公式:我们可以从两个方向推导
「不选物品」其实就是dp[i-1][j] ,等效于我们只考虑前 i-1 件物品,当前容量为 j 的情况下的最大价值。同理,如果我们选第 i 件物品的话,代表消耗了 weight[i] 的背包容量,获取了 value[i] 的价值,那么留给前 i-1 件物品的背包容量就只剩 j-weight[i]。即最大价值为dp[i-1][j-weight[i]]+v[i].
得到递推公式:dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+v[i])。
(3)、初始化dp数组:首先当 j=0 时候,那么无论选什么物品总和一定为0,所以dp[i][0]初始化为0.
从递推公式中可以看出dp[i][j]是从左上角和上面得到,所以当i=0时候就要初始化dp数组。
dp[0][j],即 i=0时,表示存放编号为0的物品时候,各个容量的背包所能存放的最大价值。代码如下:
for(int j = weight[0]; j <= W; j++)
dp[0][j] = value[0];(4)代码解答
#include <iostream>
using namespace std;
#include <vector>
#include <algorithm>
void maxValue()
{
vector<int> weight{ 3,4,6,8 };
vector<int> value{ 8,9,11,12 };
int W = 13;
vector<vector<int>> dp(weight.size() + 1, vector<int>(W + 1, 0));
for (int j = weight[0]; j <= W; j++)
{
dp[0][j] = value[0];
}
for (int i = 1; i < weight.size(); i++)
{
for (int j = 0; j <= W; j++)
{
if (j < weight[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j],dp[i-1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][W] << endl;
}
int main()
{
maxValue();
return 0;
}一维dp解法
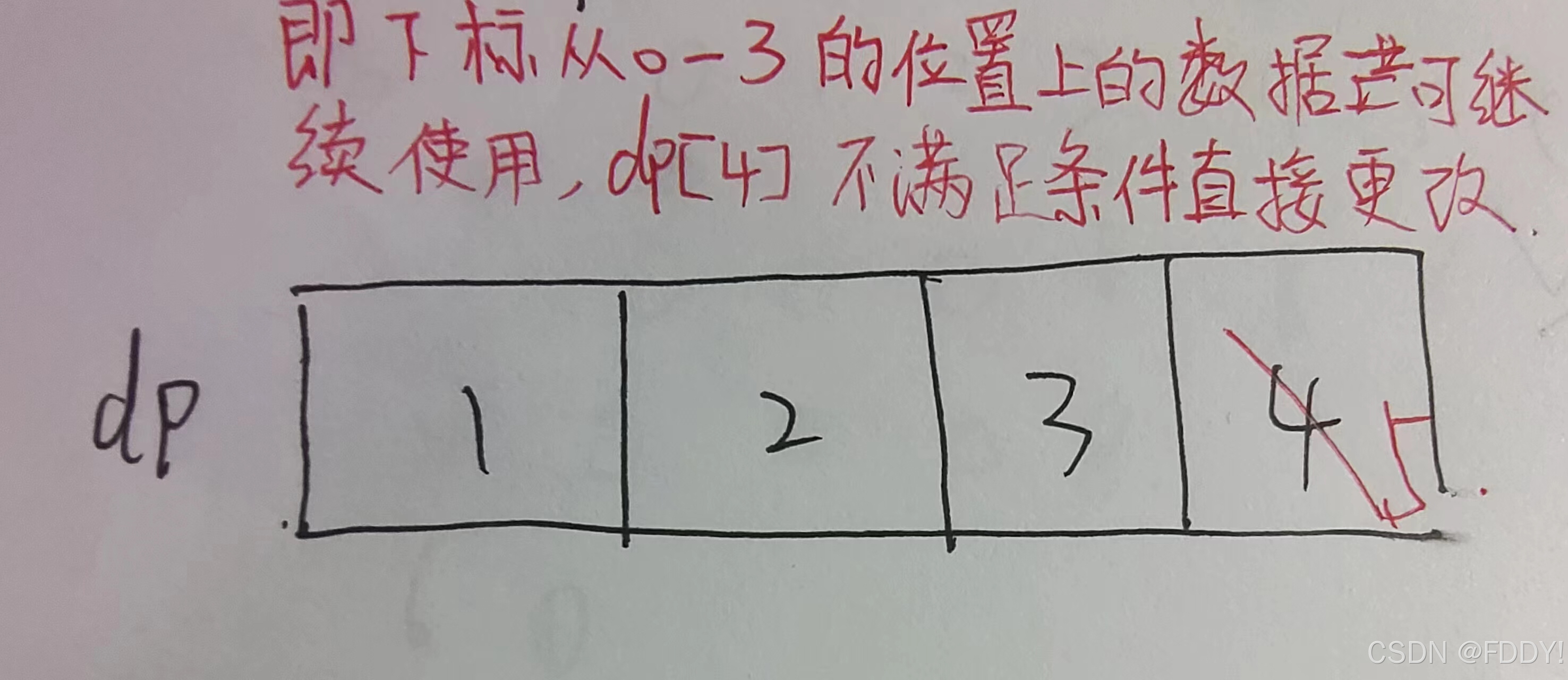
主要思想:顾名思义使用一维数组,在上一组数据的基础上改变,不重新开辟一个数组空间。不再将dp[i-1] 这一层的数据复制到 dp[i] 层上,而是直接使用 dp[j]。即满足条件的上一层数据可以重复使用,不满足的直接在原位置改变。(说的可能有点模糊,不要慌直接看图)
(1)、确定dp数组及其下标的含义:dp[j]表示容量为j的背包所背物品的最大价值。
(2)、确定递推公式:
「不选物品」其实就是dp[j] ,等效于我们只考虑前 i-1 件物品,当前容量为 j 的情况下的最大价值。同理,如果我们选第 i 件物品的话,代表消耗了 weight[i] 的背包容量,获取了 value[i] 的价值,那么留给前 i-1 件物品的背包容量就只剩 j-weight[i]。即最大价值为dp[j-weight[i]]+v[i].
得到递推公式:dp[j]=max(dp[j],dp[j-weight[i]]+v[i])。
(3)、初始化一维dp数组:首先当 j=0 时候,那么无论选什么物品总和一定为0,所以dp[i][0]初始化为0。然后从递推公式中看出是 dp[j-weight[i]]+v[i] 和 dp[j] 取最大值,所以我们需要赋值为0,防止过程中的价值被初始值覆盖。
(4)、遍历顺序:这个是一维dp和二维dp最关键的地方
一维dp数组遍历背包的时候背包容量是从大到小的遍历,二维dp数组遍历背包的时候背包容量是从小到大的。从大到小遍历背包容量只会将物品 i 放入背包一次,从小到大遍历会多次加入物品i,这是因为背包容量从大到小遍历每次遍历每次取得的状态不会和之前的状态重合,这样每件物品之只遍历一次:如图所示
(5)、代码
#include <iostream>
using namespace std;
#include <vector>
#include <algorithm>
void maxValue()
{
vector<int> weight{ 3,4,6,8 };
vector<int> value{ 8,9,11,12 };
int W = 13;
vector<int> dp(W + 1, 0);
for (int i = 0; i < weight.size(); i++)
{
for (int j = W; j >= weight[i]; j--)
{
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[W] << endl;
}
int main()
{
maxValue();
return 0;
}二、【完全背包】问题
有N件物品和一个最多能背重量为W的背包。每个物品都有无限个(一件物品即可以选择多次),求将哪些物品放入背包中物品价值的总和最大。
输入样例:weight[3,4,6,8 ] value[ 8,9,11,12 ] W=13;
(1)、主要思想:【完全背包】和【0-1背包】问题的区别:【0-1】背包问题的每种物品只可以选择一次,而完全背包问题的每种物品可以选择多次。(非常重要)
(2)、解法:因为【0-1背包】和【完全背包】的只要差别在与选择一件物品的次数,所以由上述【0-1】背包的一维dp解法中可知,只需要改变背包容量的遍历方向,即从大到小改为从小到大即可重复使用每件物品,so直接上代码
(3)、代码
#include <iostream>
using namespace std;
#include <vector>
#include <algorithm>
void maxValue()
{
vector<int> weight{ 3,4,6,8 };
vector<int> value{ 8,9,11,12 };
int W = 13;
vector<int> dp(W + 1, 0);
for (int i = 0; i < weight.size(); i++)
{
for (int j = weight[i]; j <= W; j++)
{
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[W] << endl;
}
int main()
{
maxValue();
return 0;
}总结
以上便是本章的所有内容,可能有些地方有不足,欢迎评论区指正,觉得博主写的还行的话请点个小赞赞谢谢各位。