计算机组成结构—高速缓冲存储器(Cache)

一、Cache的基本工作原理

1.Cache工作原理

2.命中率

3.Cache的基本结构

概为了解决 CPU 和主存之间速度不匹配的问题，计算机系统中引入了高速缓存（Cache）的念。基本想法就是使用速度更快但容量更小、价格更高的 SRAM 制作一个缓冲存储器，用来存放经常用到的信息；这样一来，CPU 就可以直接与 Cache 交换数据，而不用访问主存了。

这种方案之所以有效，是因为通过对大量典型程序分析发现，在一定时间内，CPU 要从主存取指令或者数据，只会访问主存局部的地址区域。这是由于指令和数据在内存中都是连续存放的，而且有些指令和数据会被多次调用（比如常用函数、循环代码段、数组和一些常数）；也就是说，指令和数据在主存中地址分布不是随机的，而是相对的簇聚。这使得 CPU 执行程序时，访存具有相对的局部性；这称为程序访问的 局部性原理。

时间局部性：如果一个数据现在被访问了，那么以后很有可能也会被访问
空间局部性：如果一个数据现在被访问了，那么它周围的数据在以后可能也会被访问

局部性原理是 Cache 高效工作的理论基础。

一、Cache的基本工作原理

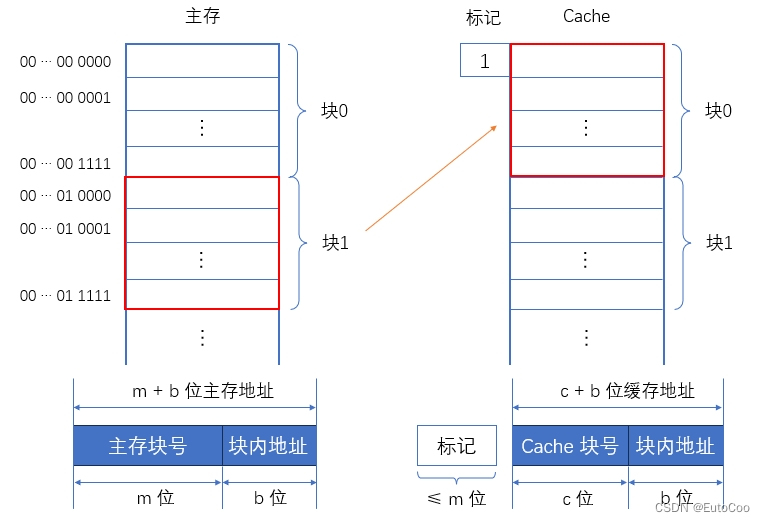
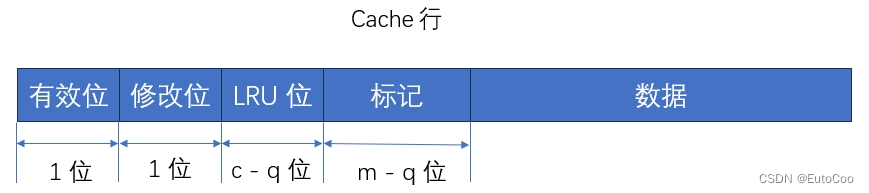
为了便于 Cache 与主存交换信息，Cache 和主存都被划分为相等的块。Cache 块又称 Cache 行，每块由若干字节组成，块的长度称为块长。由于 Cache 的容量远小于主存的容量，所以 Cache 中的块数要远少于主存中的块数，Cache 中仅保存主存中最活跃的若干块的副本。

1.Cache工作原理

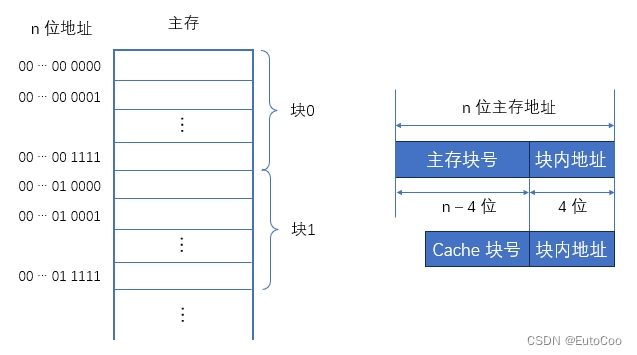
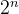
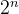
假设主存按字节编址，地址用 n 位二进制码表示，那么主存容量为 $2^{n}$ B；块的大小为 16 个字节，那么主存中块的个数为： $2^{n}$ / 16 = $2^{n-4}$ 。那么如果对每个块也做一个编号，其实就对应着地址中的前 n - 4 位。

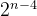
这样，主存地址就分成了两部分：高 n - 4 位表示主存中的 “块地址”，低 4 位表示 “块内地址”，块内地址其实就是具体存储字在块内的 “偏移量”。类似，Cache 中地址也可以分成这样的两部分，由于 Cache 中块长与主存一致，所以低 4 位同样是块内地址；剩余的高位则为 Cache 的块号。Cache 的块号位数小于 n - 4。

所以，可按照某种策略预测 CPU 在未来一段时间内要访存的数据，将其装入 Cache。当 CPU 要读取主存中的某个字时，分为两种情况：

Cache 命中：需要的字已经在缓存中，就将其地址转换为缓存地址，直接访问 Cache，与主存无关；
Cache 未命中：需要的字不在缓存中，仍需访问主存，并将该字所在的块一次性地从主存调入 Cache。

如果某个主存块已经调入 Cache，就称该主存块和 Cache 中的缓存块建立了对应关系。由于 Cache 容量有限，当 Cache 已满时，就需要根据某种替换算法，让需要调入 Cache 的块替换之前某个缓存块的内容。所以，一个缓存块不可能永远只对应一个主存块；需要给每个缓存块设置一个标记，当写入对应的主存块号后，表示它当前存放了哪个主存块。

CPU 与 Cache 之间的数据交换，通常是以字为单位；而 Cache 与主存之间的数据交换则以块为单位。

2.命中率

Cache 的效率，通常用 命中率 来衡量。命中率是指 CPU 要访问的信息已经在 Cache 中的比率。Cache 的容量和块长都是影响命中率的重要因素。

假设一个程序执行期间，访问 Cache 的总命中次数为 Nc，访问主存的总次数为 Nm，那么命中率为：

$h = \frac{N_c}{N_c + N_m}$

设 tc 为命中时的 Cache 访问时间，tm 为未命中时的主存访问时间，那么 Cache - 主存系统的平均访问时间 ta 为：

$t_a = ht_c + (1-h)t_m$

由于 tc 远小于 tm，因此平均访问时间 ta 越接近 tc 就说明 Cache 效率越高。用 e 表示访问效率，则有：

$e = \frac {t_c}{t_a} \times 100\% = \frac{t_c}{ht_c + (1-h)t_m} \times 100\%$

命中率 h 越接近 1，访问效率就高。一般来说，Cache 容量越大，命中率就越高；而块长与命中率的关系较为复杂，它取决于程序的局部特性，一般取每块 4 ~ 8 个可编址单位（字或字节）效果较好。

3.Cache的基本结构

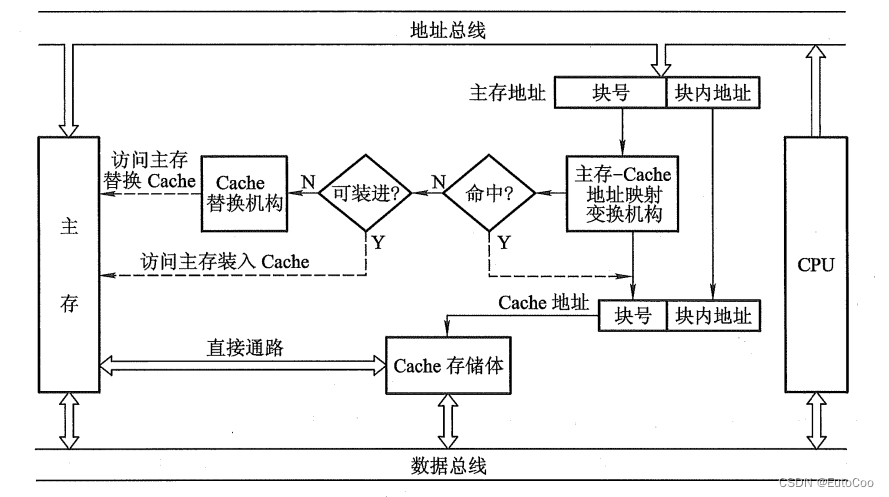
Cache 主要由 Cache 存储体、主存 - Cache 地址映射变换机构、Cache 替换机构几大模块组成。

（1）Cache 存储体

Cache 存储体以块为单位与主存交换信息，Cache 访存的优先级最高。

（2）主存 - Cache 地址映射变换机构

地址映射变换机构会将 CPU 送来的主存地址转换为 Cache 地址。由于主存和 Cache 块长相同，所以块内地址是不变的，地址变换主要就是主存的块号（高位地址）到 Cache 块号之间的转换。这涉及到一个函数的映射关系，被称为 地址映射。

（3）Cache 替换机构

地址转化之后，如果 Cache 命中，CPU 就直接访问 Cache 存储体；如果不命中，CPU 需要访问主存将需要的字取出，并把它所在的主存块调入 Cache。如果 Cache 已满，无法将主存块直接调入 Cache，就需要 Cache 内的替换机构执行替换策略。

所谓替换策略，就是按一定的替换算法，确定从 Cache 中移出哪个块返回主存，并把新的主存块调入 Cache 进行替换。

在执行写操作时，还需要考虑如何使 Cache 如何与主存的内容保持一致。这就需要用某种 Cache 写策略。

4.Cache的改进

Cache 的改进，主要就是由一个缓存改为使用多个缓存。主要有两个方向：增加 Cache 级数；将统一的 Cache 变为分立的 Cache。

（1）两级缓存

最初在 CPU 和主存之间只设一个缓存，称为 单一缓存。随着集成电路密度的提高，这个缓存就直接与 CPU 集成在了一个芯片中，所以又称为 片内缓存（片载缓存）。

由于片内缓存容量无法做到很大，所以可以考虑在片内缓存和主存之间再加一级缓存，称为 片外缓存，也由 SRAM 组成。这种由片外缓存和片内缓存构成的 Cache 系统被称为 “两级缓存”，片内缓存作为第一级（L1 Cache），片外缓存作为第二级（L2 Cache）。

（2）分立缓存

指令和数据都存放在同一缓存内的 Cache，称为 统一缓存；而 分立缓存 则将指令和数据分别存放在两个缓存中，一个叫指令 Cache，另一个叫数据 Cache。这两种缓存的选择主要考虑两个因素：

主存结构。如果计算机主存中指令、数据是统一存储的，则相应的 Cache 采用统一缓存；如果主存指令、数据分开存储，则相应的 Cache 采用分立缓存。
机器对指令执行的控制方式。如果采用了超前控制或者流水线控制方式，一般都采用分立缓存。所谓超前控制，是指在当前指令执行尚未结束时就提前把下一条准备执行的指令取出；而所谓流水线控制，就是多条指令同时分阶段执行。

二、Cache和主存之间的映射方式

Cache 块中的信息是主存中某个块的副本，地址映射是指把主存地址空间映射到 Cache 地址空间，这相当于定义了一个函数：

Cache 地址 = f ( 主存地址 )

当然，由于 Cache 和主存块长一样，而块内地址只是字在当前块内的 “偏移量”，所以映射转换之后块内地址是不变的。我们需要的其实只是 Cache 块号和主存块号之间的函数关系：

Cache 块号 = f ( 主存块号 )

Cache 块远少于主存块，所以 Cache 块不可能永远对应唯一的主存块，需要在 Cache 中为每一个块加一个标记，指明它是主存中哪一块的副本。这个标记的内容，应该能够唯一确定对应主存块的编号。另外，为了说明 Cache 行中的信息是否有效，每个 Cache 行还需要有一个 有效位，该位为 1 时，表示 Cache 中该映射的主存块数据有效；为 0 则无效。

地址映射的方法有以下 3 种。

1.直接映射

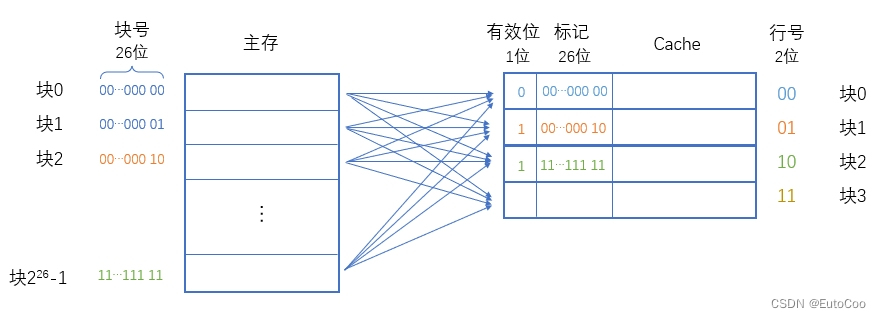
直接映射 的思路非常简单，就是 “挨个对应”，主存中的每一块只能装入 Cache 中的唯一位置。由于 Cache 容量很小，当主存中的块已经 “遍历” 完所有 Cache 地址后，下一个主存块的对应位置就又成了 Cache 中的第一行（第一个块）。

很明显，这跟 “顺序存储” 的思路是一样的，用主存块号对 Cache 的总行数取模，就可以得到对应 Cache 的行号了：

Cache行号 = 主存块号 mod Cache总行数

例如，假设主存地址为 32 位，按字节编址，主存块大小为 64 B，所以主存块共有 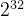$2^{32}$ / 64= $2^{26}$ 个；如果 Cache 只有 4 行（4 个块），那么采用直接映射方式的对应关系如下：

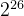
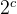
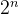
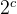
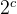
更加一般化，假设 Cache 共有 $2^{c}$ 行，主存有 $2^{m}$ 个块，那么 Cache 行号有 c 位，主存块号有 m 位。在直接映射方式中，主存块号为 0、 $2^{c}$ 、 $2^{c+1}$ ... 的块，都映射到 Cache 的第 0 行；而主存中块号为 1、 $2^{c}$ + 1、 $2^{c+1}$ +1... 的块，映射到 Cache 的第 1 行；以此类推。

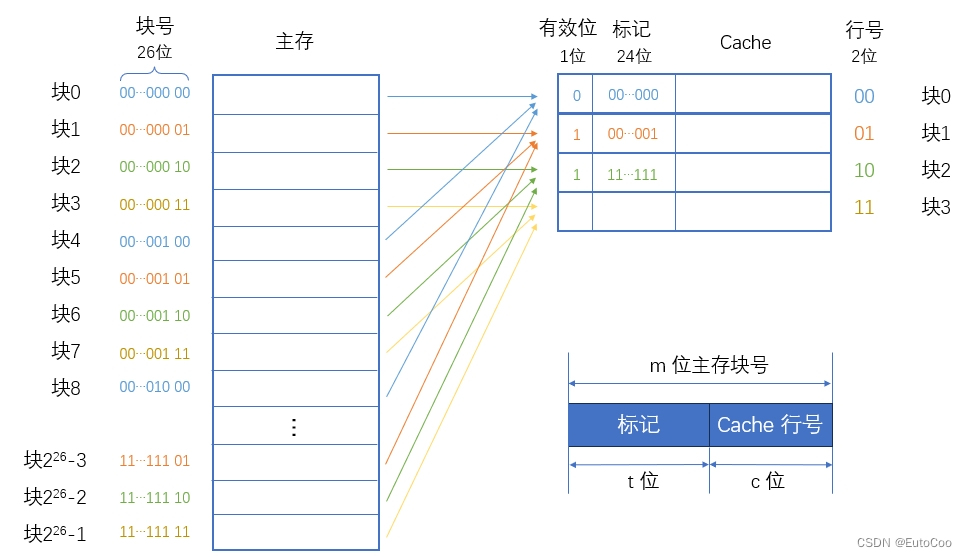
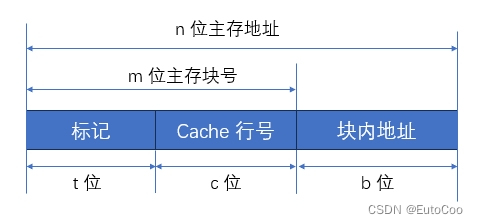
这样一来，主存块号的低 c 位就对应了 Cache 中的行号；当一个块存放在 Cache 中，只需要高 m - c 位就可以指明它对应的主存中的块号。给每个 Cache 行设置一个 t = m - c 位的标记，那么当主存某块调入 Cache 后，就将其块号的高 t 位设置在对应 Cache 行的标记中。

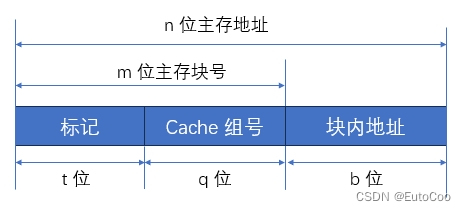
所以直接映射方式下，主存地址结构为：

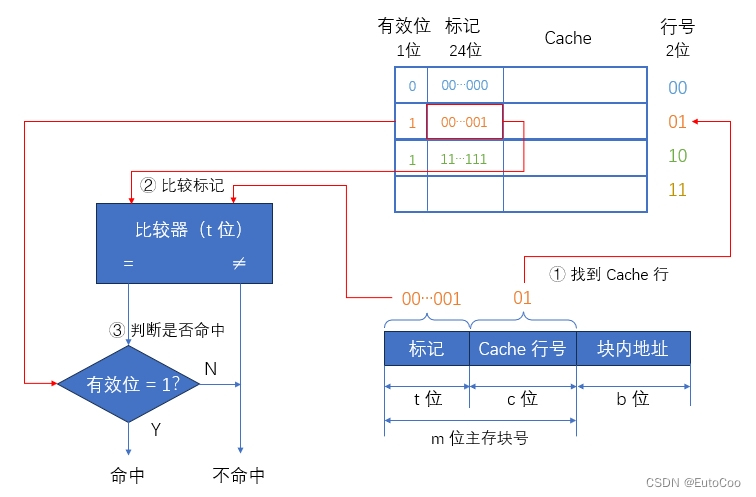
访存过程：

① 根据访存地址中间的 c 位，找到对应的 Cache 行。

② 将该 Cache 行中的标记和主存地址的高 t 位标记进行比较。

③ 若相等且有效位为1，则 Cache 命中，此时根据主存地址中低位的块内地址，在对应的 Cache 行中存取信息；若不相等或有效位为 0，则 Cache 未命中，此时 CPU 从主存中读出该地址所在的一块信息，并送至对应的 Cache 行中，将有效位置 1，并置标记为地址中的高 t 位。

直接映射实现简单，但不够灵活，即使 Cache 的其他许多地址空着也不能占用，这使得直接映射的块冲突概率高，空间利用率低。

2.全相联映射

直接映射的问题在于，我们找到的是从主存块到缓存行的一种 “多对一” 的关系，每一个主存块只能对应唯一的缓存行，从而导致冲突概率高。如果让一个主存块，可以映射到多个缓存块上，变成 “多对多” 的关系，明显就可以减少冲突了。

最简单的情况，就是不加任何条件限制，让主存的每一个块都可以映射到 Cache 的任意位置；简单来说就是 “有空就填”，放在哪里都可以。这就是 全相联映射 方式。

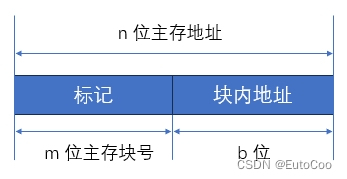
由于没有任何规律，所以当一个块存放在 Cache 中，无法根据 Cache 行号推出它对应主存块的任何信息；因此必须在每行的标记中明确指出该行取自主存的哪一块，这样标记就需要完整的 m 位主存块号。CPU 访存时，需要与所有 Cache 行的标记进行比较。

全相联映射方式下，主存的地址结构为：

全相联映射方式的优点是灵活，Cache块的冲突概率低，空间利用率高，命中率也高；缺点是标记的速度较慢，实现成本较高，通常需采用昂贵的按内容寻址的相联存储器进行地址映射。

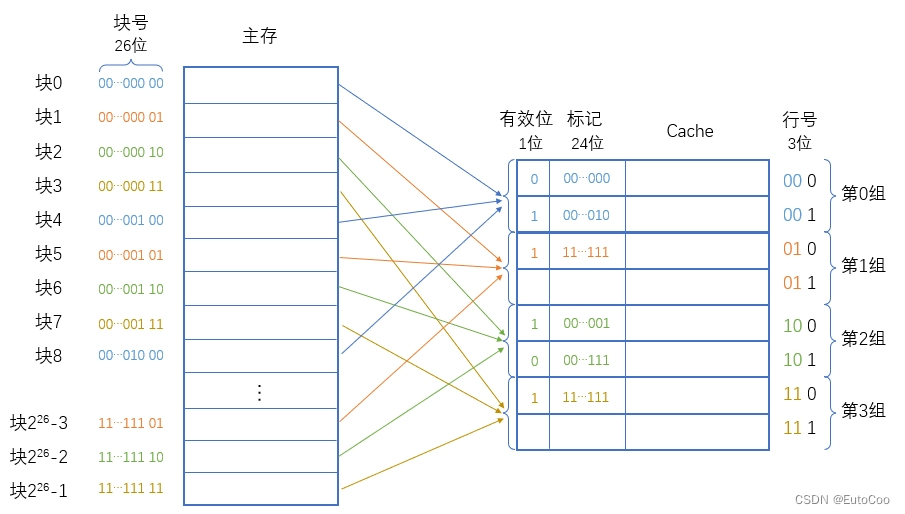
3.组相联映射

把直接映射和全相联映射两种方式结合起来，就是 组相联映射 方式。

组相联的思路是将 Cache 分成 Q 个大小相等的组，每个主存块可装入对应组的任意一行；它所在的组则按顺序依次排列得到。也就是 组间采用直接映射、而 组内采用全相联映射 的方式。当 Q=1 时，变为全相联映射；当 Q = Cache 行数时变为直接映射。

假设每组有 R 个 Cache 行，则称之为 R 路组相联；例如每组有 2 个 Cache 行时称为 2 路组相联。

类似的例子，假设主存地址为 32 位，按字节编址，主存块大小为 64 B，所以主存块共有 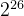$2^{26}$ 个；如果 Cache 有 8 行（8 个块），采用 2 路组相联映射方式，那么共有 Q = 8 / 2 = 4 组。对应关系如下：

可以看出，现在的 “组号” 就相当于直接映射方式下的行号，可以由主存块号对组数 Q 取模得到：

Cache组号 = 主存块号 mod Cache组数

更加一般化，假设 Cache 共有 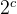$2^{c}$ 行，分为 Q = $2^{q}$ 组，主存有 $2^{m}$ 个块；那么 Cache 行号有 c 位，其中高 q 位是组号，主存块号有 m 位。这时每组中的 Cache 行数为 R = $2^{c}$ / Q = $2^{c-q}$ ，行号的低 c - q 位就代表了 Cache 行在组内的序号。

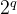
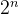
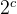
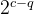
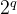
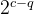
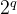
在 R 路组相联映射方式中，主存块号为 0、 $2^{q}$ 、 $2^{q+1}$ ... 的块，都映射到 Cache 的第 0 组，可以选择组内 $2^{c-q}$ 行的任一行；而主存中块号为 1、 $2^{q}$ + 1、 $2^{q+1}$ + 1... 的块，映射到 Cache 的第 1 组，同样可以任选组内的 Cache 行；以此类推。

这样一来，主存块号的低 q 位就对应了 Cache 中的组号；当一个块存放在 Cache 中，只需要高 m - q 位就可以指明它对应的主存中的块号。给每个 Cache 行设置一个 t = m - q 位的标记，那么当主存某块调入 Cache 后，就将其块号的高 t 位设置在对应 Cache 行的标记中。

所以组相联映射方式下，主存地址结构为：

访存过程：

① 先根据访存地址中间的 Cache 组号，找到对应的 Cache 组。

② 然后将该组中每个 Cache 行的标记与主存地址的高位标记进行比较。

③ 若有一个相等且有效位为1，则 Cache 命中，此时根据主存地址中的块内地址，在对应 Cache 行中存取信息；若都不相等，或虽相等但有效位为 0，则 Cache 未命中，此时 CPU 从主存中读出该地址所在的一块信息，并送至对应 Cache 组的任意一个空闲行，将有效位置 1，并设置标记。

组相联映射方式下，路数 R 越大，即每组 Cache 行的数量越多，发生块冲突的概率越低，但比较电路也越复杂。

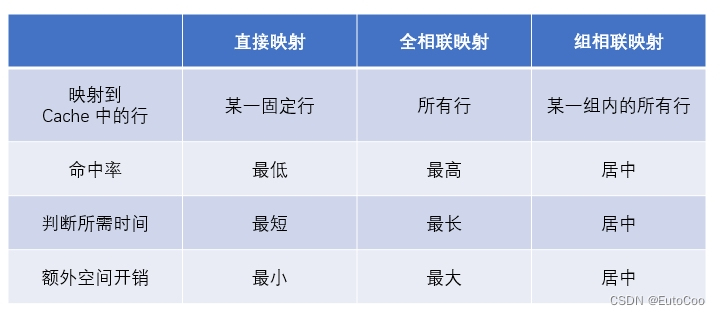
可以将以上 3 中映射方式对比如下：

三、Cache中主存块的替换算法

如果有新的主存块需要调入 Cache，而可用空间又已经占满，这时就需要替换掉某个旧块，这就产生了替换策略（替换算法）的问题。当采用直接映射时，替换的位置是固定的，无须考虑替换算法；而在采用全相联映射或组相联映射时，就需要使用替换算法来确定到底置换哪个 Cache 行。

常用的替换算法有 随机（RAND）算法、先进先出（FIFO）算法、最近最少使用（LRU）算法 和 最不经常使用（LFU）算法。其中最常考查的是 LRU 算法。

随机算法：随机地确定替换的 Cache 块。实现简单，但未依据局部性原理，命中率较低。
先进先出算法（Fisrt In First Out，FIFO）：选择最早调入的行进行替换。实现简单，但也未依据局部性原理。
最近最少使用算法（Least Recently Used，LRU）：依据局部性原理，选择近期最久未访问过的 Cache 行作为被替换的行。LRU 算法为每个 Cache 行设置一个计数器，用来记录每个块的使用情况，并根据计数值选择淘汰某个块。
最不经常使用算法（Least Frequently Used，LFU）：将一段时间内访问次数最少的 Cache 行换出。与 LRU 类似，也设置一个计数器，Cache 行建立后从 0 开始计数，每访问一次计数器加 1，需要替换时将计数值最小的行换出。

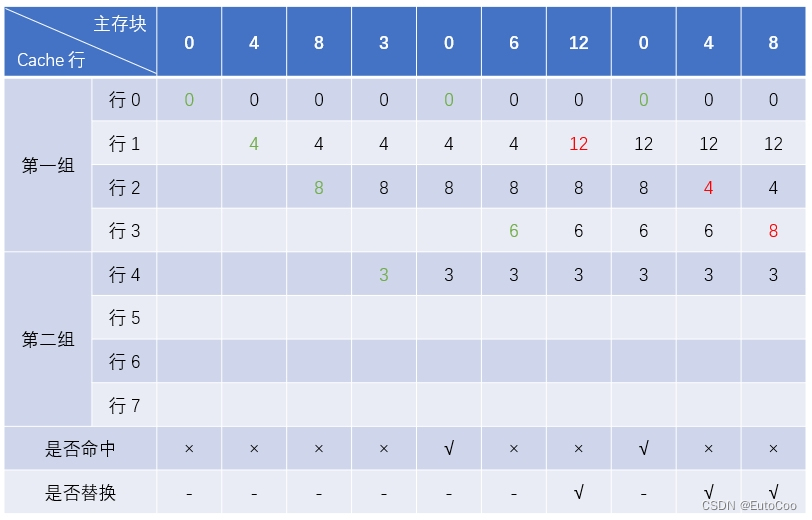
例如，假设一台机器 Cache 有 8 个行，初始值为空，采用 4 路组相联映射方式和 LRU 替换策略，当顺序访问主存块号为 0，4，8，3，0，6，12，0，4，8 时，缓存的命中和替换情况如下：

LRU 算法中利用计数器来表示 Cache 行未被访问的时间。整体原则是：当 Cache 行有新的主存块调入时，计数器开始计数，初始值为 0，此后每遇到一次对 Cache（或 Cache 组）的访问就加 1；如果一次访问 Cache 命中了这一行，就将计数器清 0；每次有 Cache 行计数器清 0，其它行的计数器依然要加 1，不过只需要计数值比当前行更小的那些继续加 1 就可以了。

需要替换时，直接选择计数值最大的行，调入新的块并将计数器置 0。这是由于不同的Cache 行不会同时开始计数，且每次都同步加 1，所以所有 Cache 行的计数值都不会相同，每次发生替换时必然能够找到一个最大值；而一旦有计数器清 0，比它计数值更大的那些也是都不加 1，依然保持着原有的大小顺序。

这样一来，如果当前 Cache 共有 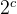$2^{c}$ 行，分为 Q = $2^{q}$ 组，每组行数为 R = $2^{c}$ / Q = $2^{c-q}$ ，那么计数器的值就不会超过 R；只要用 c - q 位就可以表示计数器了，这被叫做 LRU 位。因此，计数值的位数与 Cache 组的大小有关。当为 2 路时有 1 位 LRU 位，4 路时有 2 位 LRU 位。LRU 位会同标记、有效位一同作为 Cache 的一部分。

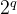
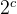
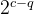
四、Cache的写策略

因为 Cache 中的内容是主存块内容的副本，当对 Cache 中的内容进行更新时，就需选用写操作策略使 Cache内容和主存内容保持一致。此时分两种情况：

（1）Cache 写命中（要修改的单元在 Cache 中）

这种情况有两种处理方法：

写直达法

也叫全写法、写穿透法。将数据同时写入 Cache 和主存。这种方法实现简单，一致性好。缺点是降低了速度，时间开销为访存时间。为了减少写入主存的开销，可以在 Cache 和主存之间加一个写缓冲。

写回法

也叫回写法、写返回法。数据只写入 Cache，而不立即写入主存，只有当此块被换出时才写回主存。这种方法效率很高，但一致性较差。在每个 Cache 行中设置一个修改位（脏位），若修改位为 1（“脏”），则说明对应 Cache 行中的块被修改过，替换时须写回主存；若修改位为 0（“净”），则替换时无须写回主存。

（2） Cache 写未命中（要修改的单元不在 Cache中）

这种情况也有两种处理方法：

写分配法

把数据写入主存，同时将该块调入Cache。这种方法依据了空间局部性原理。

非写分配法

只把数据写入主存，不进行调块。

非写分配法通常与全写法合用，写分配法通常与回写法合用。

这样，还是之前的机器，采用组相联映射的 Cache 共有 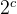$2^{c}$ 行，分为 Q = $2^{q}$ 组，主存有 $2^{m}$ 个块；那么 Cache 行号有 c 位，其中高 q 位是组号，主存块号有 m 位。这时每组中的 Cache 行数为 R = $2^{c}$ / Q = $2^{c-q}$ ，即采用 R 路组相联映射，假如还采用了 LRU 替换策略和回写法，那 Cache 行应该包含以下部分：

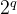
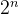
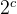
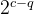
现代计算机通常设立多级 Cache，一般两级 Cache 按离 CPU 的远近分别命名为 L1 Cache、L2 Cache，离 CPU 越近则速度越快、容量越小。指令 Cache 与数据 Cache 分离一般在 L1 级，LI Cache 对 L2 Cache 使用全写法，L2 Cache 对主存使用回写法。由于L2 Cache的存在，避免了因频繁写而造成写缓冲溢出的情况。