算法之旅：LeetCode 拓扑排序由简入繁完全攻略

前言

欢迎来到我的算法探索博客，在这里，我将通过解析精选的LeetCode题目，与您分享深刻的解题思路、多元化的解决方案以及宝贵的实战经验，旨在帮助每一位读者提升编程技能，领略算法之美。
👉更多高频有趣LeetCode算法题

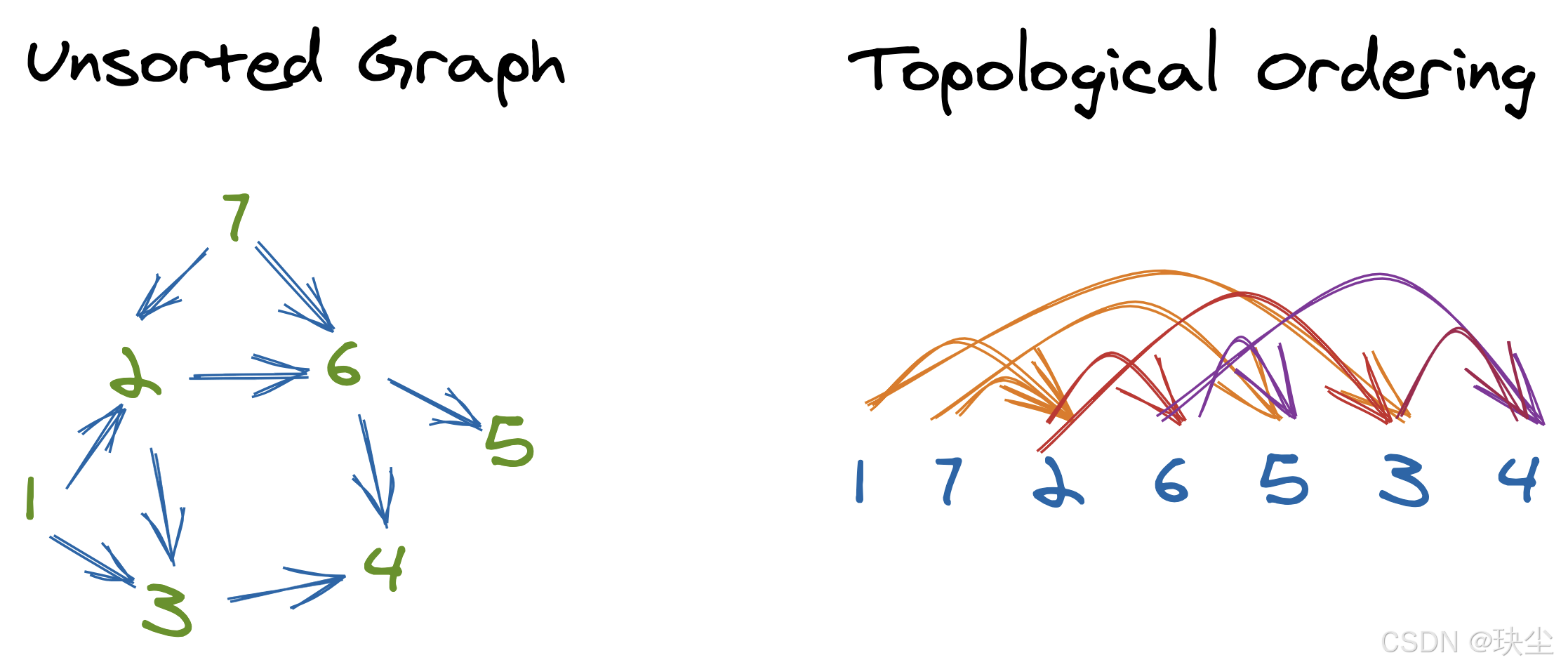
拓扑排序是一种适用于有向无环图（DAG）的重要算法，常用于解决依赖关系问题，如课程安排、任务调度等。在本文中，我们将通过以下四道题目，详细讲解拓扑排序的原理、实现方式及其多样化应用场景：

1557. 可以到达所有点的最少点数目	207. 课程表
210. 课程表 II	802. 找到最终的安全状态

在这里插入图片描述

拓扑排序基础知识

核心思想：

拓扑排序旨在为图中的节点安排一种线性顺序，使得对每条有向边 (u, v)，节点 u 总是排在 v 之前。

本节我们利用 入度表 + 广度优先搜索（BFS） 实现拓扑排序：

入度的概念

每个节点的入度是指有多少条边指向这个节点。
如果某个节点的入度为 0，说明它没有依赖，可以作为起点开始。

拓扑排序的原理

将所有入度为 0 的节点加入队列（表示这些节点可以直接开始，不需要经过任何依赖）。
从队列中逐一取出节点，将其所有出边的目标节点的入度减 1 (被引用次数-1)。
如果某个节点的入度变为 0，将其加入队列。
重复这一过程，直到队列为空。
如果完成所有节点的拓扑排序，说明图中无环；否则，说明存在环。

适用条件：

图必须是 有向无环图（DAG）。
若存在环，则无法构建拓扑排序。

常见实现方法：

Kahn算法： 基于入度统计。逐步移除入度为 0 的节点，动态更新图结构。
DFS（深度优先搜索）： 通过后序遍历逆序输出结果。

实战：经典例题讲解

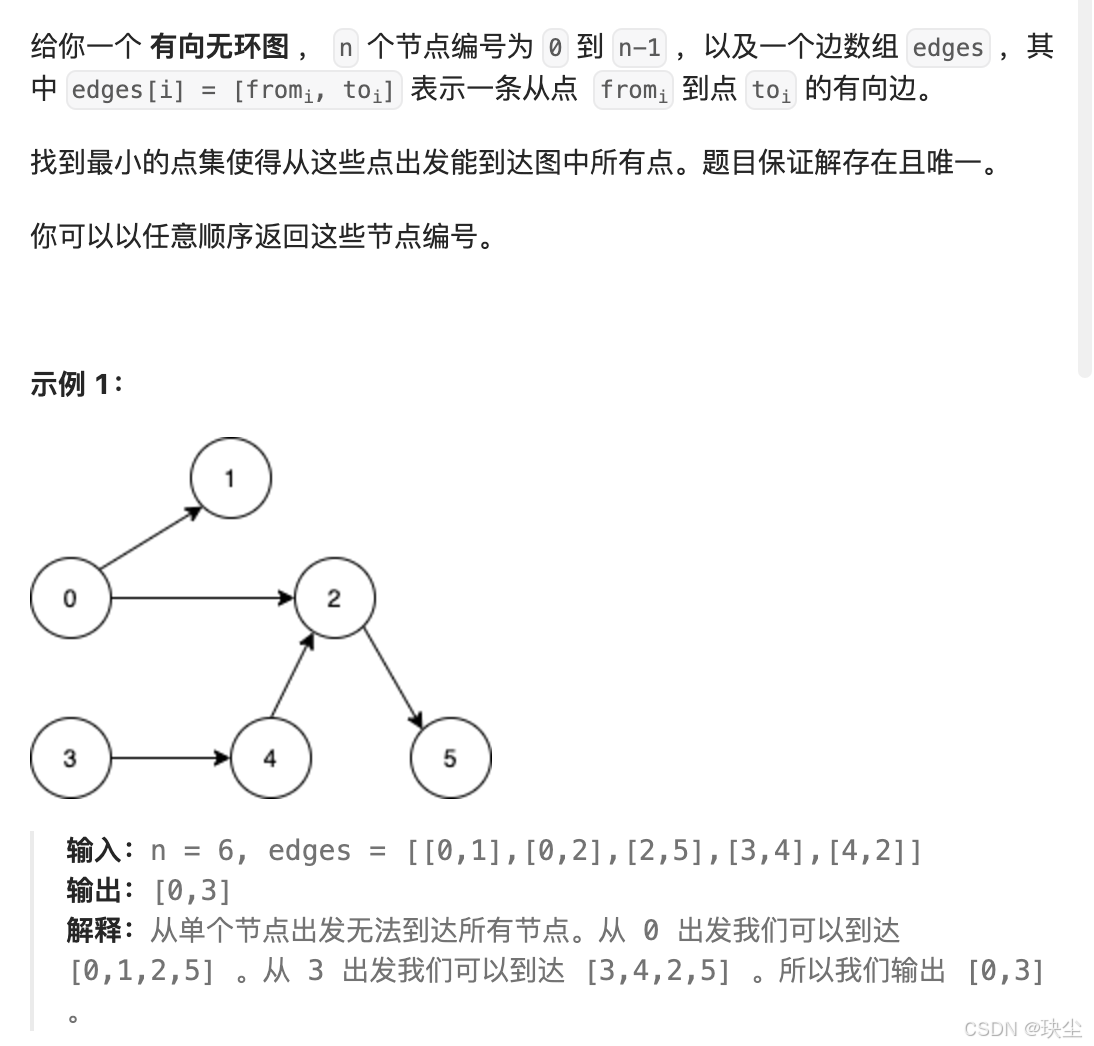
1557. 可以到达所有点的最少点数目

🪸题目描述

在这里插入图片描述

🪷核心思路

这是一个经典的入度问题，这题可以看作是 拓扑排序思想的局部应用，利用入度信息快速判断需要作为起点的节点。初具雏形。
若一个节点的入度为 0，则必须从它出发才能到达该节点。
因此，我们只需要找出所有入度为 0 的节点即可。

构建入度数组

for(List<Integer> a : edges){
    inDegree[a.get(1)]++;
}

遍历所有边，计算每个节点的入度 （即有多少条边指向该节点，被引用的次数） 。
结果存储在 inDegree 数组中，其中 inDegree[i] 表示节点 i 的入度。

找出入度为 0 的节点

for (int i = 0; i < n; i++) {
    if (inDegree[i] == 0) {
        res.add(i);
    }
}

遍历所有节点，检查哪些节点的入度为 0。
入度为 0 的节点没有任何依赖，它们必须作为路径的起点，加入结果列表 res。

返回结果
最终返回 res，即所有入度为 0 的节点构成的集合。

🌿代码实现

Java

class Solution {
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
        List<Integer> res = new ArrayList<>();
        int[] inDegree = new int[n];

        // 构建入度数组
        // 其中每个元素表示对应被依赖的次数，也就是 入度
        for(List<Integer> a : edges){
            inDegree[a.get(1)]++;
        }

        // 将所有入度为 0 的课程加入队列
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (inDegree[i] == 0) {
                res.add(i);
            }
        }
        return res;
    }
}

Python

class Solution(object):
    def findSmallestSetOfVertices(self, n, edges):
        """
        :type n: int
        :type edges: List[List[int]]
        :rtype: List[int]
        """
        # 初始化入度数组
        in_degree = [0] * n
        
        # 构建入度数组
        for edge in edges:
            in_degree[edge[1]] += 1
        
        # 找出所有入度为 0 的节点
        return [i for i in range(n) if in_degree[i] == 0]

C++

class Solution {
public:
    vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {
        // 初始化入度数组
        vector<int> inDegree(n, 0);

        // 构建入度数组
        for (const auto& edge : edges) {
            inDegree[edge[1]]++;
        }

        // 找出所有入度为 0 的节点
        vector<int> result;
        for (int i = 0; i < n; ++i) {
            if (inDegree[i] == 0) {
                result.push_back(i);
            }
        }

        return result;
    }
};

207. 课程表

🪸题目描述

在这里插入图片描述

🪷核心思路

这是一道经典的图是否有环的问题，可以通过 Kahn算法 或 DFS 判断环的存在。

利用 入度表 + 广度优先搜索（BFS） 实现拓扑排序。

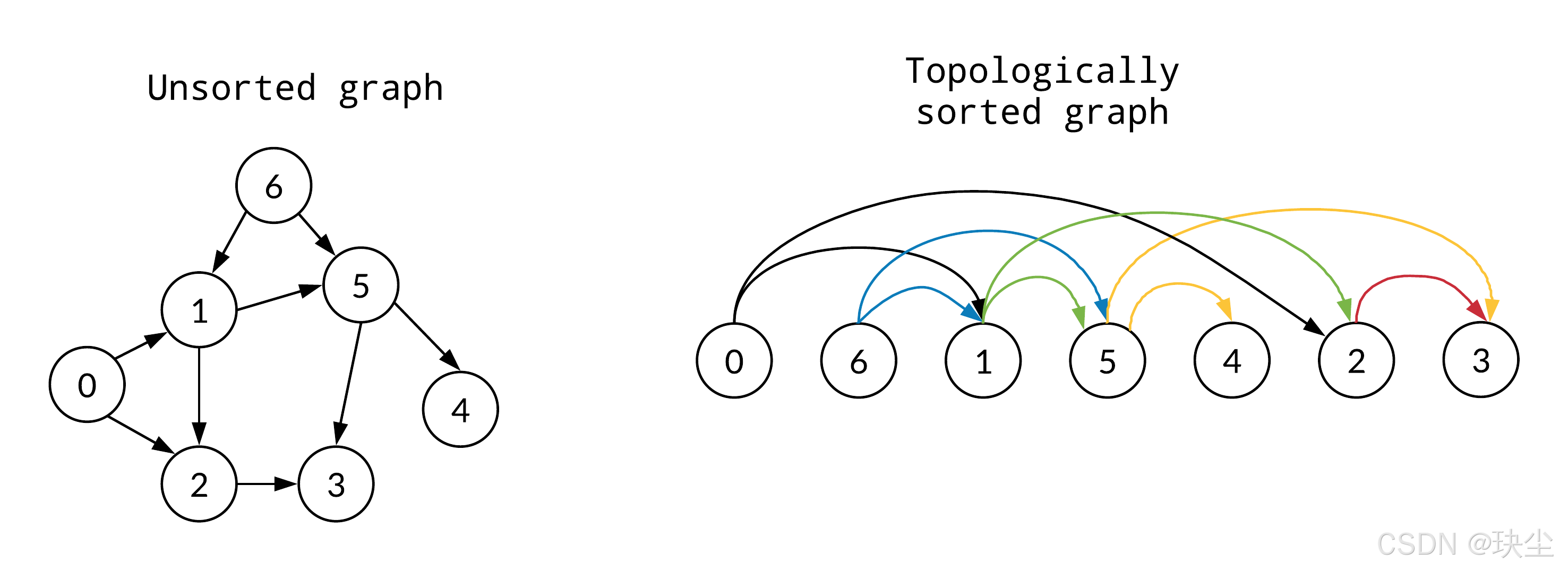
比上一题多了一步的就是加了一个邻接表，目的就是把两个点的有向连接（图二）表示出来进行BFS遍历求得结果。

在这里插入图片描述

🌿代码实现

Java

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 入度数组，表示每个课程被依赖的次数
        int[] inDegree = new int[numCourses];
        // 图的邻接表表示
        List<List<Integer>> adjacency = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            adjacency.add(new ArrayList<>());
        }
        // 构建图和入度数组
        for (int[] pair : prerequisites) {
            inDegree[pair[0]]++;
            // 每个课程（节点）都有一个列表，列表中存储的是所有依赖于该课程的其他课程（即该课程是其他课程的先修课程）
            adjacency.get(pair[1]).add(pair[0]);
        }

        // 将所有 入度为 0 的课程加入队列，表示这些课程可以直接学习，无需先修课程。
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        // BFS 遍历
        int count = 0; // 记录已完成的课程数量
        while (!queue.isEmpty()) {
            int course = queue.poll();
            count++;
            for (int nextCourse : adjacency.get(course)) {
                inDegree[nextCourse]--;
                // 添加接下来 入度为0 的元素
                if (inDegree[nextCourse] == 0) {
                    queue.offer(nextCourse);
                }
            }
        }

        // 当 BFS 结束时，如果拓扑排序数组中的课程数小于总课程数，说明图中存在环，无法完成所有课程。这时，返回空数组 []
        return count == numCourses;
    }
}

Python

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """
        # 入度数组，表示每个课程被依赖的次数
        in_degree = [0] * numCourses
        # 图的邻接表表示
        adjacency = [[] for _ in range(numCourses)]

        # 构建图和入度数组
        for pair in prerequisites:
            in_degree[pair[0]] += 1
            adjacency[pair[1]].append(pair[0])

        # 将所有 入度为 0 的课程加入队列，表示这些课程可以直接学习，无需先修课程。
        queue = []
        for i in range(numCourses):
            if in_degree[i] == 0:
                queue.append(i)

        # BFS 遍历
        count = 0  # 记录已完成的课程数量
        while queue:
            course = queue.pop(0)
            count += 1
            for next_course in adjacency[course]:
                in_degree[next_course] -= 1
                if in_degree[next_course] == 0:
                    queue.append(next_course)

        # 如果拓扑排序中的课程数小于总课程数，说明存在环，无法完成所有课程
        return count == numCourses

C++

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        // 入度数组，表示每个课程被依赖的次数
        vector<int> inDegree(numCourses, 0);
        // 图的邻接表表示
        vector<vector<int>> adjacency(numCourses);

        // 构建图和入度数组
        for (const auto& pair : prerequisites) {
            inDegree[pair[0]]++;
            adjacency[pair[1]].push_back(pair[0]);
        }

        // 将所有 入度为 0 的课程加入队列，表示这些课程可以直接学习，无需先修课程。
        queue<int> q;
        for (int i = 0; i < numCourses; ++i) {
            if (inDegree[i] == 0) {
                q.push(i);
            }
        }

        // BFS 遍历
        int count = 0; // 记录已完成的课程数量
        while (!q.empty()) {
            int course = q.front();
            q.pop();
            count++;
            for (int nextCourse : adjacency[course]) {
                inDegree[nextCourse]--;
                if (inDegree[nextCourse] == 0) {
                    q.push(nextCourse);
                }
            }
        }

        // 如果拓扑排序中的课程数小于总课程数，说明存在环，无法完成所有课程
        return count == numCourses;
    }
};

210. 课程表 II

🪸题目描述

在这里插入图片描述

🪷核心思路

和 207. 课程表 类似，但需要输出一条合法的课程学习路径。我们可以直接基于拓扑排序构造学习路径。

🌿代码实现

Java

class Solution {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        // 入度数组，表示每个课程被依赖的次数
        int[] inDegree = new int[numCourses];
        // 图的邻接表表示
        List<List<Integer>> adjacency = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            adjacency.add(new ArrayList<>());
        }
        // 构建图和入度数组
        for (int[] pair : prerequisites) {
            inDegree[pair[0]]++;
            adjacency.get(pair[1]).add(pair[0]);
        }

        // 将所有入度为 0 的课程加入队列
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        // 保存课程学习顺序
        int[] order = new int[numCourses];
        int index = 0; // 指向 `order` 数组的位置

        // BFS 遍历
        while (!queue.isEmpty()) {
            int course = queue.poll();
            order[index++] = course; // 将课程加入学习顺序
            for (int nextCourse : adjacency.get(course)) {
                inDegree[nextCourse]--;
                if (inDegree[nextCourse] == 0) {
                    queue.offer(nextCourse);
                }
            }
        }

        return index < numCourses ? new int[0] : order; // 返回课程学习顺序
    }
}

Python

class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: List[int]
        """
        # 入度数组，表示每个课程被依赖的次数
        in_degree = [0] * numCourses
        # 图的邻接表表示
        adjacency = [[] for _ in range(numCourses)]

        # 构建图和入度数组
        for pair in prerequisites:
            in_degree[pair[0]] += 1
            adjacency[pair[1]].append(pair[0])

        # 将所有入度为 0 的课程加入队列
        queue = []
        for i in range(numCourses):
            if in_degree[i] == 0:
                queue.append(i)

        # 保存课程学习顺序
        order = []
        while queue:
            course = queue.pop(0)
            order.append(course)
            for next_course in adjacency[course]:
                in_degree[next_course] -= 1
                if in_degree[next_course] == 0:
                    queue.append(next_course)

        # 如果拓扑排序未覆盖所有课程，返回空数组
        return order if len(order) == numCourses else []

C++

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        // 入度数组，表示每个课程被依赖的次数
        vector<int> inDegree(numCourses, 0);
        // 图的邻接表表示
        vector<vector<int>> adjacency(numCourses);

        // 构建图和入度数组
        for (const auto& pair : prerequisites) {
            inDegree[pair[0]]++;
            adjacency[pair[1]].push_back(pair[0]);
        }

        // 将所有入度为 0 的课程加入队列
        queue<int> q;
        for (int i = 0; i < numCourses; ++i) {
            if (inDegree[i] == 0) {
                q.push(i);
            }
        }

        // 保存课程学习顺序
        vector<int> order;
        while (!q.empty()) {
            int course = q.front();
            q.pop();
            order.push_back(course);
            for (int nextCourse : adjacency[course]) {
                inDegree[nextCourse]--;
                if (inDegree[nextCourse] == 0) {
                    q.push(nextCourse);
                }
            }
        }

        // 如果拓扑排序未覆盖所有课程，返回空数组
        return order.size() == numCourses ? order : vector<int>();
    }
};

802. 找到最终的安全状态

🪸题目描述

在这里插入图片描述

🪷核心思路

我们可以从反向图出发，寻找出度为 0 的节点（终点），并依次标记为安全。

为什么反向图能够帮助我们找到安全节点？

从安全节点开始反向查找：

安全节点是指没有环的节点，因此从这些节点出发无法到达其他节点，因此它们的反向图中入度为 0。
一旦节点的入度为 0，意味着没有节点依赖它，它是“安全”的。

拓扑排序的过程：

在反向图中，拓扑排序会找到所有的“无依赖”节点（即入度为 0 的节点），这些节点可以认为是安全的。
通过拓扑排序，如果某个节点进入队列并被处理，说明它没有环，并且在反向图中是可以到达终点的。

🌿代码实现

Java

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        // 反向图 + 拓扑排序
        int n = graph.length;
        List<List<Integer>> reverseGraph = new ArrayList<>();
        int[] inDegree = new int[n];
        for (int i = 0; i < n; i++) {
            reverseGraph.add(new ArrayList<>());
        }

        for (int i = 0; i < n; i++) {
            for (int next : graph[i]) {
                reverseGraph.get(next).add(i);
                inDegree[i]++;
            }
        }
        
        // 2. 将所有入度为 0 的节点加入队列（安全节点）
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        // 3. 拓扑排序
        List<Integer> safeNodes = new ArrayList<>();
        while (!queue.isEmpty()) {
            int node = queue.poll();
            safeNodes.add(node);
            for (int prev : reverseGraph.get(node)) {
                // 如果当前节点是某个节点的依赖节点，减少它的入度
                inDegree[prev]--;
                if (inDegree[prev] == 0) {
                    queue.offer(prev);  // 如果该节点的入度为 0，说明它是安全节点
                }
            }
        }
        
        // 4. 返回所有安全节点（按升序排序）
        Collections.sort(safeNodes);
        return safeNodes;
    }
}

Python

class Solution(object):
    def eventualSafeNodes(self, graph):
        """
        :type graph: List[List[int]]
        :rtype: List[int]
        """
        n = len(graph)
        reverseGraph = [[] for _ in range(n)]
        inDegree = [0] * n
        # 构建反向图并计算入度
        for i in range(n):
            for next_node in graph[i]:
                reverseGraph[next_node].append(i)
                inDegree[i] += 1
        
        # 将所有入度为 0 的节点加入队列
        queue = deque()
        for i in range(n):
            if inDegree[i] == 0:
                queue.append(i)
        
        # 拓扑排序
        safeNodes = []
        while queue:
            node = queue.popleft()
            safeNodes.append(node)
            for prev in reverseGraph[node]:
                inDegree[prev] -= 1
                if inDegree[prev] == 0:
                    queue.append(prev)
        
        # 返回所有安全节点，按升序排序
        safeNodes.sort()
        return safeNodes

C++

class Solution {
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<vector<int>> reverseGraph(n);
        vector<int> inDegree(n, 0);
        
        // 构建反向图和计算每个节点的入度
        for (int i = 0; i < n; ++i) {
            for (int next : graph[i]) {
                reverseGraph[next].push_back(i);  // 反向图
                inDegree[i]++;  // 计算入度
            }
        }
        
        // 将所有入度为 0 的节点加入队列
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (inDegree[i] == 0) {
                q.push(i);
            }
        }

        // 拓扑排序
        vector<int> safeNodes;
        while (!q.empty()) {
            int node = q.front();
            q.pop();
            safeNodes.push_back(node);
            for (int prev : reverseGraph[node]) {
                if (--inDegree[prev] == 0) {
                    q.push(prev);
                }
            }
        }
        
        // 返回所有安全节点，按升序排序
        sort(safeNodes.begin(), safeNodes.end());
        return safeNodes;
    }
};

结语

通过这四道题，我们可以看到拓扑排序的强大应用：

解决 依赖问题，如课程安排（207, 210）。
处理 图中状态分类 的问题，如安全状态（802）。
分析 关键点或入度特性，如找到最小的起点集合（1557）。

拓扑排序不仅是一种算法，更是一种理解图结构的思维方式。在面试中，遇到类似依赖关系的题目，尝试从有向图的角度切入往往是一个很好的突破点。

如果您渴望探索更多精心挑选的高频LeetCode面试题，以及它们背后的巧妙解法，欢迎您访问我的博客，那里有我精心准备的一系列文章，旨在帮助技术爱好者们提升算法能力与编程技巧。

👉更多高频有趣LeetCode算法题

在我的博客中，每一篇文章都是我对算法世界的一次深入挖掘，不仅包含详尽的题目解析，还有我个人的心得体会、优化思路及实战经验分享。无论是准备面试还是追求技术成长，我相信这些内容都能为您提供宝贵的参考与启发。期待您的光临，让我们共同在技术之路上不断前行！