目录

实验内容：

实验过程：

1.算法设计

2.程序清单

3.复杂度分析

4.运行结果

实验内容：

删除二叉树的子树:假设二叉树中的结点均不相等，采用二叉链存储，设计递归算法删除根结点值为x的子树。

实验过程：

1.算法设计

设计了一个基于字符输入表达式来创建、打印和删除二叉树节点的功能。主要算法设计过程为：

• 创建二叉树：

1.输入一个字符串，其中包含括号、逗号以及代表节点值的字符。

2.通过遍历字符串，根据字符类型执行相应的操作当遇到'('时，表示进入新的子树，将当前父节点压入栈中并标记即将创建的是左子树；当遇到')'时，表示子树创建完成，弹出栈顶元素；当遇到','时，表示开始创建当前节点的右子树；对于其它字符（即节点值），创建一个新的二叉树节点，并根据当前状态将其链接到相应父节点的左或右子节点。

• 打印二叉树：使用递归方法，从根节点开始，按照先序遍历的方式打印节点值及括号以表示子树结构。
• 删除节点及其子节点：从给定的根节点开始递归地释放所有子节点和根节点的内存。
• 查找并删除指定值节点：定义一个递归函数SearchBiTNode，它在二叉树中查找具有指定值的节点。在查找过程中，当找到目标节点时，调用FreeBiTNode函数删除该节点，并返回true表示删除成功。如果在递归查找过程中没有找到目标节点，则返回false。

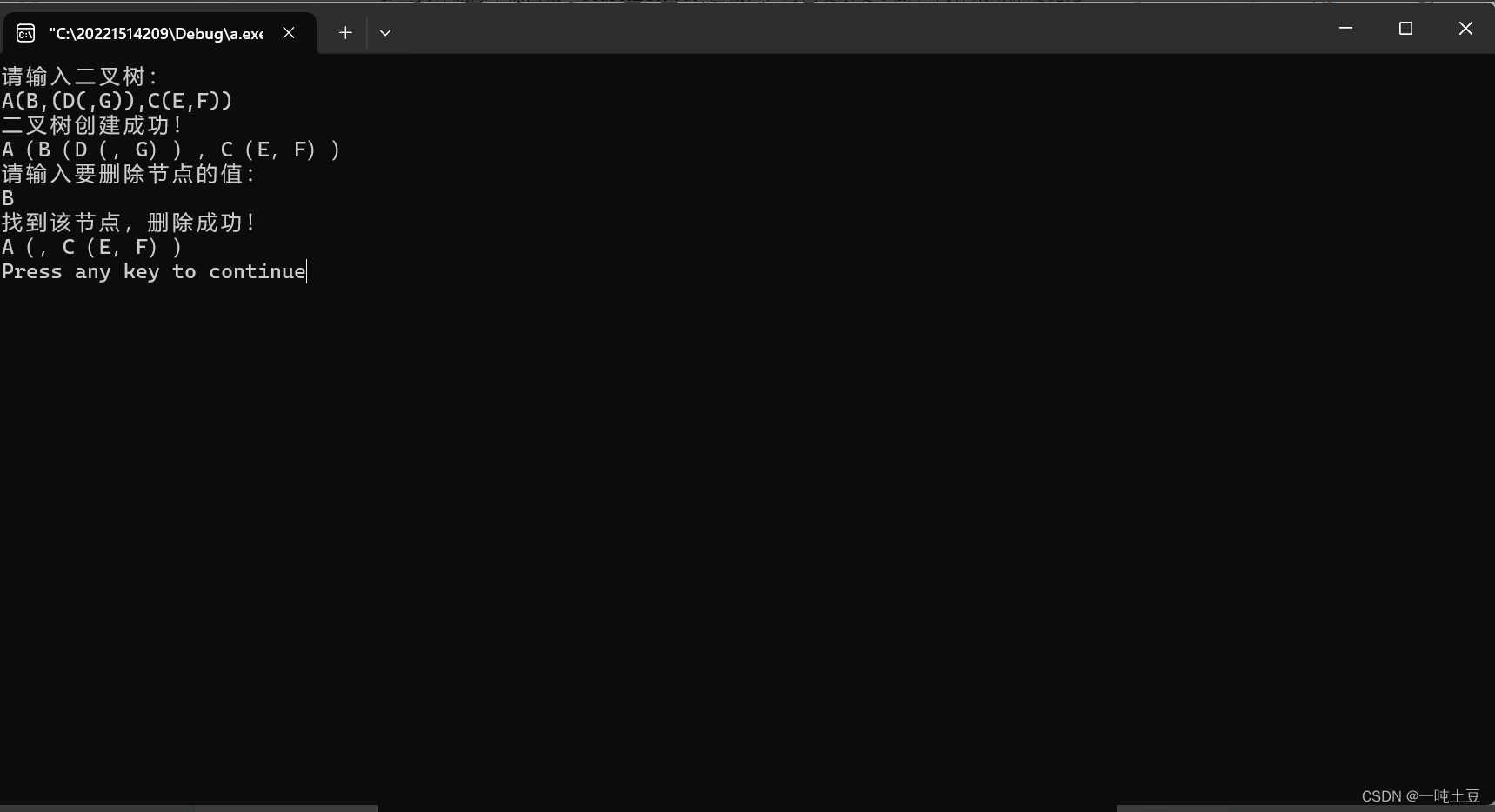
主函数流程：创建二叉树，打印创建好的二叉树。输入要删除的节点值，然后进行查找和删除操作。在删除成功的情况下再次打印删除节点后的二叉树。

2.程序清单

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 100

//定义二叉树节点结构体
typedef struct BiTNode{
    char data;
    struct BiTNode *lchild, *rchild;
} BiTNode;

//从给定字符串str中创建二叉链表
void CreatBiTNode(BiTNode * &b,char * str)
{	
	//定义BiTNode指针数组Temp,初始化一个指向BiTNode结构体的指针变量p
	BiTNode *Temp[MAXSIZE],*p = NULL;
	//栈顶指针，记录当前正在处理的子树的父节点
	int top = -1;
    int k;
	int j=0;
	char ch=str[j];

	//初始化二叉树为空
	b = NULL;

	while(ch != '\0')
	{
		switch(ch)
		{
			case '(': //遇到（，表示进入新的子树，栈顶指针+1，该节点压入栈中
				top++;
				Temp[top] = p;
				k = 1;//该节点的左子树
				break;

			case ')'://子树创建成功，栈顶指针-1
				top--;
				break;

			case ',':
				k = 2;// 遇到该节点的右子树
				break;

			default ://如果是节点数据,创建一个新的节点
				p = (BiTNode *)malloc(sizeof(BiTNode));
				//当前字符为节点的数据
				p -> data = ch;
				//左右指针为空
				p -> lchild = p -> rchild = NULL;

				//如果当前树为空，将新创建的节点设为根节点
				if(b == NULL)
					b = p;
				else
				{
					if(k == 1)
						Temp[top] -> lchild = p;//将新节点设置为栈顶元素的左孩子
					else if(k == 2)
						Temp[top] -> rchild = p;//右孩子
				}
		}
		//移动下一个字符
		j++;
		ch = str[j];
	}
}

//输出二叉树
void PrintBiTNode(BiTNode *b)
{
	if(b != NULL)
	{
		printf("%c",b -> data);//先输出根节点
		if(b -> lchild != NULL || b -> rchild != NULL)
		{
			//有孩子时输出孩子
			printf("（");
			PrintBiTNode(b -> lchild);//递归输出左孩子
			if(b -> rchild != NULL)
			{
				printf("，");//有右孩子时输出
				PrintBiTNode(b -> rchild);//递归输出右孩子
			}
			printf("）");//孩子输出结束
		}
	}
}

//删除节点及其子节点
void FreeBiTNode(BiTNode *&b)
{
	if(b != NULL)
	{
		FreeBiTNode(b -> lchild);//递归删除左子树
		FreeBiTNode(b -> rchild);//递归删除右子树
		free(b);//释放根节点空间
		b = NULL;
	}
}

//查找节点值为Del的节点
bool SearchBiTNode(BiTNode *&b,char Del)
{
	if(b == NULL)
		return false;//树为空，找不到该节点，返回false
	if(b -> data == Del)
	{
		FreeBiTNode(b);//找到要删除的节点，调用删除函数将其删除
		printf("找到该节点，删除成功！\n");
		return true;
	}
	else if(SearchBiTNode(b -> lchild,Del))
		return true;//递归查找其左子树，找到节点，返回true		
	else if(SearchBiTNode(b -> rchild,Del))
		return true;//递归查找其右子树，找到节点，返回true
	else
		return false;
}


void main()
{
	//定义二叉树
	BiTNode *b;
	//要删除子树的值
	char Del;
	char str[MAXSIZE];
	printf("请输入二叉树：\n");
	scanf("%s",&str);
	//创建二叉树
	CreatBiTNode(b,str);
	printf("二叉树创建成功！\n");
	//输出二叉树
	PrintBiTNode(b);
	printf("\n");
	printf("请输入要删除节点的值：\n");
	//清空缓冲区
	fflush(stdin);
	scanf("%c",&Del);
	if(SearchBiTNode(b,Del)){
		//输出删除后的二叉树
		PrintBiTNode(b);
	}else if(SearchBiTNode(b,Del) == false){
		printf("未查找到节点，删除失败！\n");
	}
	printf("\n");
}

3.复杂度分析

(1)时间复杂度

1.创建二叉树函数（CreatBiTNode 函数）：时间复杂度O(n),n为输入字符串的长度。因为需要遍历整个字符串来构建二叉树。

2.打印二叉树函数（PrintBiTNode 函数）：时间复杂度O(h),h为二叉树的高度，对于完全二叉树或满二叉树，其高度h接近于节点数n的对数，即h ≈ log_2(n)。

3.删除节点及其子节点函数（FreeBiTNode 函数）：时间复杂度 O(n)。在二叉链表中，每个节点最多被访问一次。对于高度为h的二叉链表，其最坏时间复杂度为O(2^h)，其中h是树的高度。对于完全二叉树或满二叉树，其高度h接近于节点数n的对数，即h ≈ log_2(n)，此时时间复杂度为O(2^(log_2(n))) = O(n)。对于非完全二叉树，实际时间复杂度可能会略小于O(n)。

4.查找并删除节点函数（SearchBiTNode 函数）：时间复杂度O(n)，同时FreeBiTNode 函数一样。最坏的情况需要遍历整个二叉树。

(2)空间复杂度

1.创建二叉树函数（CreatBiTNode 函数）：空间复杂度：代码中使用了一个大小为MAXSIZE的数组Temp作为辅助栈。在最坏情况下（输入字符串表示一个完全二叉树时），栈中最多会存放log_2(n)个节点指针（n为二叉链表的节点数）。但由于MAXSIZE是固定常数，这部分空间消耗可以认为是常数级别的。因此，这段代码的空间复杂度为O(1)

2.打印二叉树函数（PrintBiTNode 函数）：空间复杂度：递归调用会占用一定的栈空间，最坏情况下，当二叉树完全不平衡时，递归深度达到 h，因此空间复杂度为 O(h)。

3.删除节点及其子节点函数（FreeBiTNode 函数）：空间复杂度：同 PrintBiTNode 函数，递归调用也需要栈空间，最坏情况下的空间复杂度为 O(h)。

4.查找并删除节点函数（SearchBiTNode 函数）：空间复杂度：同 PrintBiTNode 和 FreeBiTNode 函数，由于也是采用递归实现，最坏情况下的空间复杂度为 O(h)。

4.运行结果