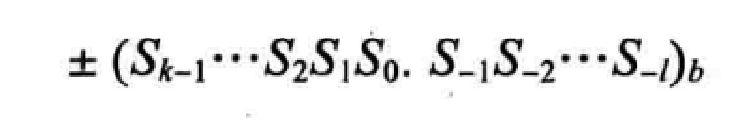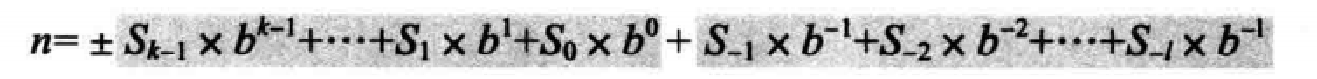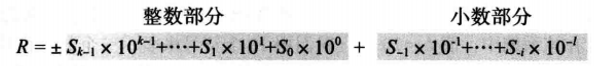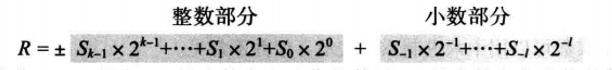第二章 数字系统
2.1 引言
什么是数字系统?
定义了用独特的符号(数码)来表示一个数字,在不同的系统中,一个数字有不同的表示方法。使用有限的数字符号来表示数字。
比如:
阿拉伯数字系统:0 1 2 3 4 5 6 7 8 9
罗马数字系统:I II III IV V VI VII…
数字系统分类:
位置化系统和非位置化系统
2.2 位置化数字系统
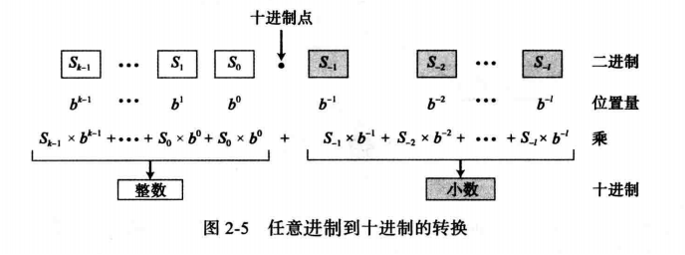
在位置化数字系统中,数字符号所占据的位置决定了其表示的值。
在该系统中,数字这样表示:
它的值是:
其中:S是一套符号集,b是底(或基数),b=S符号集中的符号总数,+/-表示数字为正或负。
2.2.1 十进制系统
符号集S={0,1,2,3,4,5,6,7,8,9}
底b=10
为了简便,通常省略括号、底、和正号。如 + ( 552.31 ) +(552.31) +(552.31)写成 552.31 552.31 552.31,底和加号是隐含的。
注意:
- 这些符号不能直接存储在计算机中
- 计算机存储正负数的方式不同
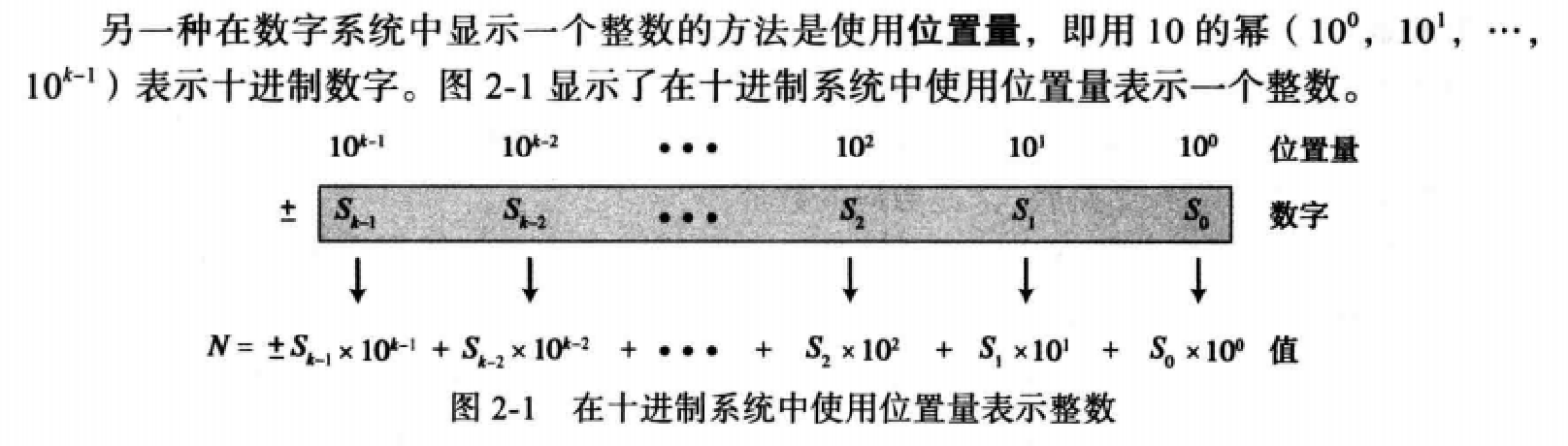
整数表示:
位置量表示:
示例:
例2-2
以下显示了在十进制系统中使用位置量表示整数-7508。我们已经使用1,10,100和1000来代替10的幂。
最大值:
有时我们需要知道可以用数码k表示的十进制整数的最大值。答案是
N
m
a
x
=
1
0
k
−
1
N_{max}=10^k-1
Nmax=10k−1。例如,如果k=5,那么这个最大值就是
N
m
a
x
=
1
0
5
−
1
=
99999
N_{max}=10^5-1=99999
Nmax=105−1=99999。
实数:
在十进制系统中,实数(带有小数部分的数字)也是我们所熟悉的。例如,使用该系统来表示元和分($23.40)整数。我们可以把实数表示为
±
S
k
−
1
…
S
1
S
0
⋅
S
−
1
…
S
−
1
\pm S_{k-1}\dots S_1S_0\cdot S_{-1}\dots S_{-1}
±Sk−1…S1S0⋅S−1…S−1,其值计算为:
其中, S 1 S_1 S1是1个数码,b=10是底,k是整数部分数码的数量, l l l是小数部分数码的数量。十进制小数点是我们用于分割整数部分和小数部分的。
示例:
2.2.2 二进制系统
符号集S={0,1}
底b=2
该系统中的符号常被称为二进制数码或**位(**位数码)
数据和程序是以二进制模式(即位模式),存储在计算机中的,这是因为计算机由电子开关制成,它们仅有开和关两种状态,1和0分别表示两种不同的状态。
整数表示:
我们可以把整数表示为
±
(
S
k
−
1
⋯
S
1
S
0
)
2
,
\pm(S_{k-1}\cdots S_{1}S_{0})_{2},
±(Sk−1⋯S1S0)2,,其值计算为:
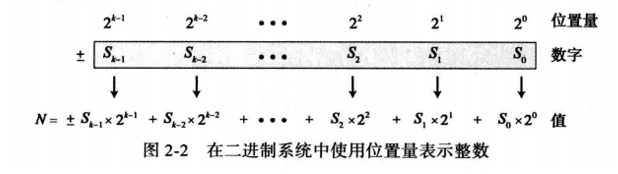
N = ± S k − 1 × 2 k − 1 + S k − 2 × 2 k − 2 + ⋯ + S 2 × 2 2 + S 1 × 2 1 + S 0 × 2 0 N=\pm S_{k-1}\times2^{k-1}+S_{k-2}\times2^{k-2}+\cdots+S_2\times2^2+S_1\times2^1+S_0\times2^0 N=±Sk−1×2k−1+Sk−2×2k−2+⋯+S2×22+S1×21+S0×20
其中, S i S_i Si是1个数码,b=2是底,k是数码的数量。
位置量表示:
另一种表示二进制数的方法是使用位置量( 2 0 2^0 20, 2 1 2^1 21, … \dots …, 2 k − 1 2^{k-1} 2k−1)。图2-2显示了在二进制系统中使用位置量表示一个数。
示例:
例2.4 以下显示了与十进制数 25 等值的二进制数 ( 11001 ) 2 (11001)_2 (11001)2。下标2表示底是 2。
注意,相等的十进制数为N=16+8+0+0+1=25。
最大值:
数码k表示的二进制整数的最大值是
N
m
a
x
=
2
k
−
1
N_{\mathrm{max}}=2^{k}-1
Nmax=2k−1。例如,如果k=5,那么这个最大值就
N
m
a
x
=
2
5
−
1
=
31
N_{\mathrm{max}}=2^{5}-1=31
Nmax=25−1=31。
实数:
在二进制系统中,一个实数(可带有小数部分的数字)可以由左边的k位和右边的位组成, ± ( S k − 1 ⋯ S 1 S 0 ⋅ S − 1 ⋯ S − l ) 2 \pm(S_{k-1}\cdots S_{1}S_{0}\cdot S_{-1}\cdots S_{-l})_{2} ±(Sk−1⋯S1S0⋅S−1⋯S−l)2,其值计算为:
其中,S是1个位,b-2是底,k是小数点左边位的数量,l是小数点右边位的数量。注意k从0开始,而l从-1开始。最高的幂是k-1且最低的是-l。
例2.5 以下显示了与十进制数 5.75 等值的二进制数 ( 101.11 ) 2 (101.11)_2 (101.11)2。
注意,相等的十进制数为R=4+0+1+0.5+0.25=5.75。
2.2.3 十六进制系统
尽管二进制系统用于存储计算机数据,但是不便于在计算机外部表示数字,因为与十进制相比,二进制符号过长。但是十进制不能直接存储在计算机中,在二进制和十进制数字之间没有显然的关系,而且它们直接的转换也不快捷。
为了克服这个问题,发明了两种位置化系统:十六进制和八进制
符号集S={0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
说明:A,B,C,D,E,F分别对应十进制中的10,11,12,13,14,15 不区分字母大小写底b = 16
整数:
我们可以把整数表示为 ± S k − 1 ⋯ S 1 S 0 \pm S_{k-1}\cdots S_1S_0 ±Sk−1⋯S1S0,其值计算为:
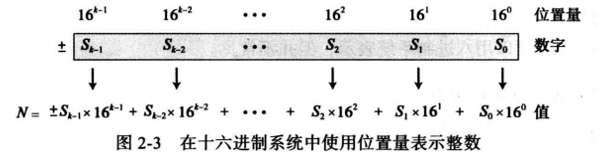
N = ± S k − 1 × 1 6 k − 1 + S k − 2 × 1 6 k − 2 + ⋯ + S 2 × 1 6 2 + S 1 × 1 6 1 + S 0 × 1 6 0 N=\pm S_{k-1}\times16^{k-1}+S_{k-2}\times16^{k-2}+\cdots+S_2\times16^2+S_1\times16^1+S_0\times16^0 N=±Sk−1×16k−1+Sk−2×16k−2+⋯+S2×162+S1×161+S0×160
其中, S i S_i Si是1个数码,b=16是底,k是数码的数量。
位置量表示:
另一种表示十六进制数的方法是使用位置量( 1 6 0 16^0 160, 1 6 1 16^1 161, … \dots …, 1 6 k − 1 16^{k-1} 16k−1)。图2-3显示了在十六进制系统中使用位置量表示一个数。
示例:
例2.6 以下显示了与十进制数 686 等值的十六进制数 ( 2 A E ) 16 (2AE)_{16} (2AE)16。
最大值:
数码k表示的十六进制整数的最大值是 N max = 1 6 k − 1 N_{\max}=16^{k}-1 Nmax=16k−1。例如,如果k=5,那么这个最大值就是 N m a x = 1 6 5 − 1 = 1048575 N_{\mathrm{max}} = 16^{5} - 1 = 1 048 575 Nmax=165−1=1048575。
实数:尽管一个实数可以用十六进制系统表示,但并不常见。
2.2.4 八进制系统
符号集S={0,1,2,3,4,5,6,7}
底b=8
八进制系统用于二进制系统的计算机外部表现形式
整数:
我们可以把整数表示为 ± S k − 1 ⋯ S 1 S 0 \pm S_{k-1}\cdots S_{1}S_{0} ±Sk−1⋯S1S0,其值计算为:
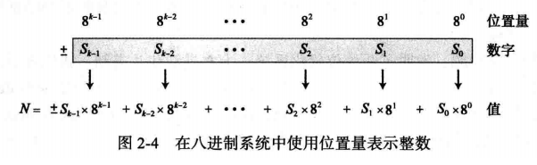
N = ± S k − 1 × 8 k − 1 + S k − 2 × 8 k − 2 + ⋯ + S 2 × 8 2 + S 1 × 8 1 + S 0 × 8 0 N=\pm S_{k-1}\times8^{k-1}+S_{k-2}\times8^{k-2}+\cdots+S_{2}\times8^{2}+S_{1}\times8^{1}+S_{0}\times8^{0} N=±Sk−1×8k−1+Sk−2×8k−2+⋯+S2×82+S1×81+S0×80
其中, S i S_i Si是1个数码,b=8是底,k是数码的数量。
另一种表示八进制数的方法是使用位置量 ( 8 0 , 8 1 , … , 8 k − 1 ) (8^0,8^1,\dots,8^{k-1}) (80,81,…,8k−1)。图2-4显示了在八进制系统中使用位置量表示一个数。
例2.7 以下显示了与十进制数 686 等值的八进制数 ( 1256 ) 8 (1256)_8 (1256)8。
注意,相等的十进制数为 N-512+128+40+6=686。
最大值
数码k表示的八进制整数的最大值是$ N_{\mathrm{max}}=8{k}-1$。例如,如果k=5,那么这个最大值就是$N_{\mathrm{max}}=8{5}-1=32 767$。
实数
尽管一个实数可以用八进制系统表示,但并不常见。
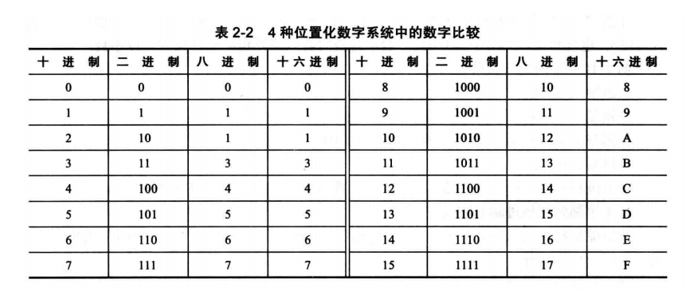
2.2.5 4种位置化数字系统小结
2.2.6 转换
什么是进制?
- 十进制逢十进一
- 二进制逢二进一
- 八进制逢八进一
- 十六进制逢十六进一
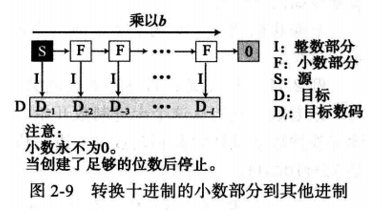
其它进制转换为十进制
其它进制转换为十进制是简单而迅速的,将数码乘以其在源系统中的位置量并求和便得到十进制中的数。
具体请参见下图:
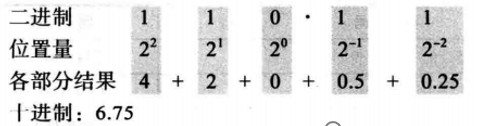
二进制进制转换为十进制:
例2.8 下面显示如何将二进制数 ( 110.11 ) 2 (110.11)^2 (110.11)2转换为十进制数6.75。
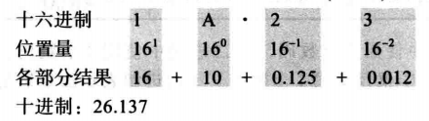
十六进制进制转换为十进制:
例2.9 下面显示如何将十六进制数 ( 1 A . 23 ) 16 (1A.23)_{16} (1A.23)16转换为十进制数。
注意这个十进制表示并不精确,因为 3 ∗ 1 6 − 2 = 0.01171875 3*16^{-2}=0.01171875 3∗16−2=0.01171875。四舍五人成3位小数(0.012),也就是说, 3 ∗ 1 6 − 2 ≈ 0.012 3*16^{-2} \approx 0.012 3∗16−2≈0.012。数字转换时我们需要指明允许保留几位小数。
八进制进制转换为十进制:
例2.10 下面显示如何将八进制数 ( 23.17 ) 8 (23.17)_8 (23.17)8转换为十进制数。
在十进制中 ( 23.17 ) 8 ≈ 19.234 (23.17)_8≈19.234 (23.17)8≈19.234。再一次,我们把 7 ∗ 8 − 2 = 0.109375 7*8^{-2}=0.109375 7∗8−2=0.109375 四舍五人。
十进制转换其它进制:
可以将十进制转换为与它等值的其它进制,需要两个过程:
- 转换整数部分
- 转换小数部分
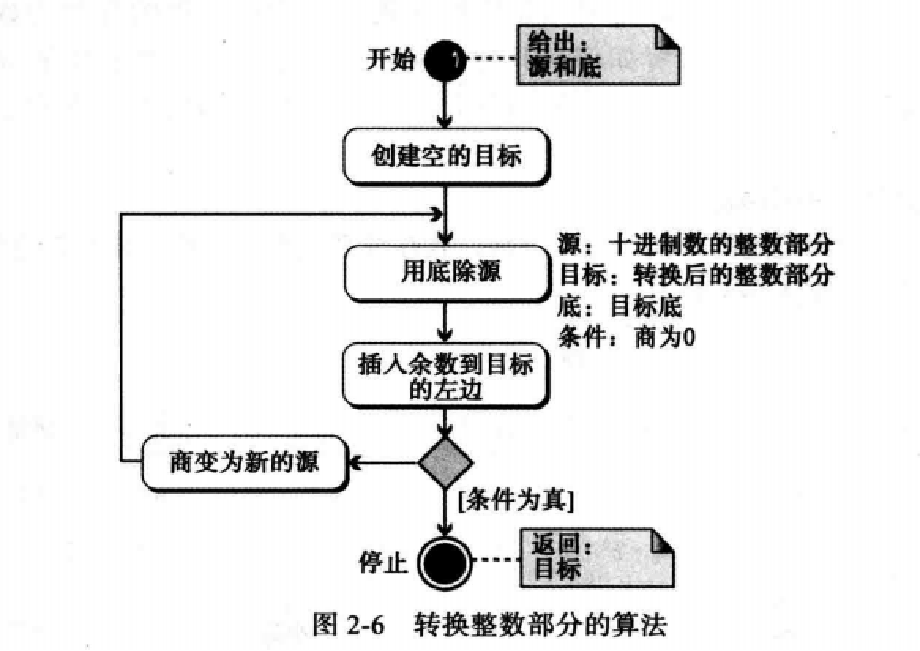
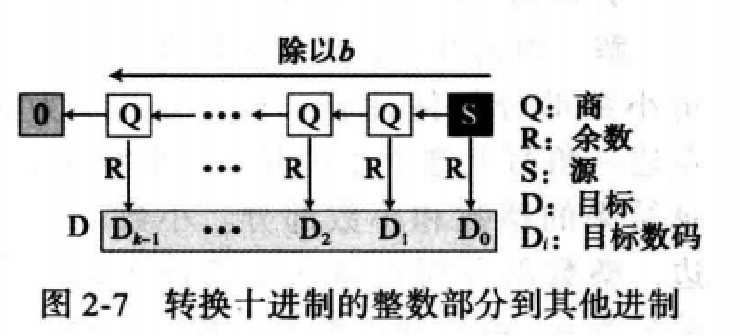
1.转换整数部分:
十进制转换二进制:
示例:
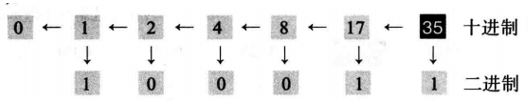
例2.11 下面演示如何将十进制数35转换为二进制数。我们从这个十进制数开始,一边连续寻找除以2得到的商和余数,一边左移。结果是$ 35=(100011)_2$。
十进制转换八进制:
示例:
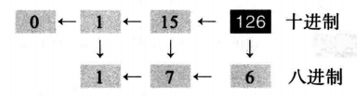
例2.12 下面演示如何将十进制数126转换为八进制数。我们一边连续寻找除以8得到的商和余数,一边左移。结果是 126 = ( 176 ) 8 126=(176)_8 126=(176)8。
十进制转换十六进制:
示例:
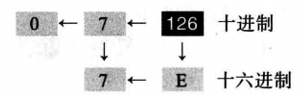
例2.13 下面演示如何将十进制数126 转换为十六进制数。我们一边连续寻找除以16得到的商和余数,一边左移。结果是 126 = ( 7 E ) 16 126=(7E)16 126=(7E)16。
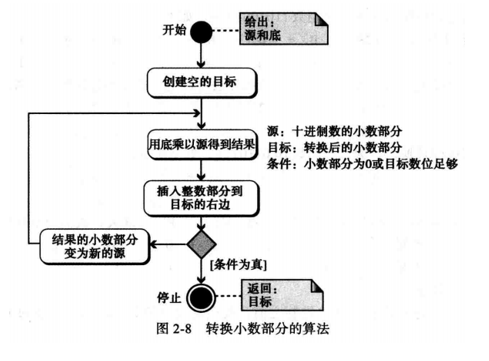
2.转换小数部分:
十进制转二进制:
示例:
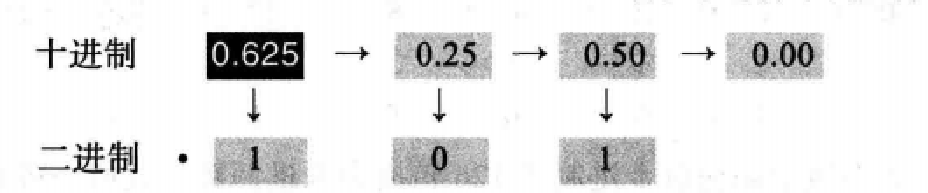
例2.14 将十进制数 0.625 转换为二进制数。
**解:**因为0.625没有整数部分,该例子显示小数部分如何计算。这里是以2为底。在左边一角写上这个十进制数。连续乘2,并记录结果的整数和小数部分。小数部分移到右边,整数部分写在每次运算的下面。当小数部分为0,或达到足够的位数时结束。结果是 0.625 = ( 0.101 ) 2 0.625=(0.101)_2 0.625=(0.101)2。
十进制转八进制:
示例:
例2.15下面演示如何将0.634转换为八进制数且精确到4位小数。结果是 0.634 = ( 0.5044 ) 8 0.634=(0.5044)_8 0.634=(0.5044)8。
十进制转十六进制:
示例:
例2.16下面演示如何将十进制数178.6转换为十六进制数且精确到1位小数。结果是 178.6 = ( B 2.9 ) 16 178.6=(B2.9)_{16} 178.6=(B2.9)16。注意,以16 为底时除或乘以 16。
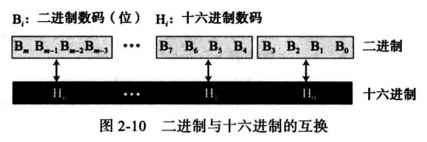
二进制&十六进制互转
我们能轻松将数字从二进制转换到十六进制,反之亦然。这是因为在这两个底之间存在一种关系:二进制中的4位恰好是十六进制中的1位。图2-10显示了该转换是如何进行的。
二进制转十六进制:
例2.19下面演示如何将二进制数 ( 10011100010 ) 2 (10011100010)_2 (10011100010)2转换为十六进制数。解 我们先将二进制数排为4位一组的形式:10011100010。注意最左边一组可能是1到4位不等。我们根据表 -2所示的值对照每组等量转换得到十六进制数 ( 4 E 2 ) 16 (4E2)_{16} (4E2)16.
十六进制转二进制:
例2.20 与十六进制数 ( 24 C ) 16 (24C)_{16} (24C)16相等的二进制数是多少?解 将每个十六进制数码转换成4位一组的二进制数:2→0010,4→0100,以及C→1100。该结果是 ( 001001001100 ) 2 (001001001100)_2 (001001001100)2。
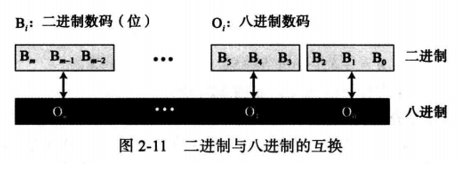
二进制&八进制互转
我们能轻松将数字从二进制转换到八进制,反之亦然。这是因为在这两个底之间存在一种关系:二进制中的3位恰好是八进制中的1位。图2-11显示了该转换是如何进行的。
二进制转八进制:
例2.21 下面演示如何将二进制数 ( 101110010 ) 2 (101110010)_2 (101110010)2转换为八进制数。
解 每3位一组转换为1位八进制数码。根据表2-2所示的值对照每3位一组等量转换得到八进制数结果是 ( 562 ) 8 (562)_8 (562)8。
八进制转二进制:
例2.22 与
(
24
)
8
(24)_8
(24)8相等的二进制数是多少?
解 将每个八进制数码写成对等的二进制位组,得到
(
010100
)
2
(010100)_2
(010100)2。
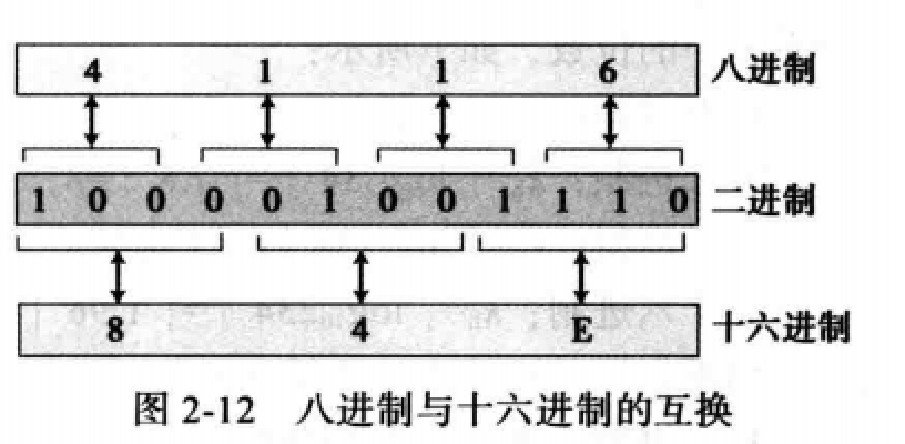
八进制&十六进制互转
八进制转十六进制,可以先转为二进制,再转为十六进制
十六进制转八进制,可以先转为二进制,再转为八进制
2.3 非位置化数字系统
八进制:**
例2.21 下面演示如何将二进制数 ( 101110010 ) 2 (101110010)_2 (101110010)2转换为八进制数。
解 每3位一组转换为1位八进制数码。根据表2-2所示的值对照每3位一组等量转换得到八进制数结果是 ( 562 ) 8 (562)_8 (562)8。
八进制转二进制:
例2.22 与
(
24
)
8
(24)_8
(24)8相等的二进制数是多少?
解 将每个八进制数码写成对等的二进制位组,得到
(
010100
)
2
(010100)_2
(010100)2。
八进制&十六进制互转
八进制转十六进制,可以先转为二进制,再转为十六进制
十六进制转八进制,可以先转为二进制,再转为八进制
[外链图片转存中…(img-PZAIWGLW-1721735557397)]
2.3 非位置化数字系统
略