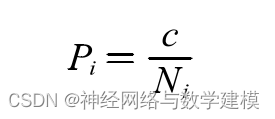目录
摘要:
多元宇宙优化算法(Multi-verse Optimization, MVO)是由S Mirjalili于2015年提出的,它源于宇宙有一个膨胀率,利用白洞具有较高的膨胀率,黑洞具有较低的膨胀率,宇宙中的粒子通过虫洞从白洞向黑洞位置转移的原理进行搜索的模拟。不管宇宙中物质的膨胀率大小,宇宙里所有的物质都会通过虫洞随机移动,到达最佳宇宙的位置。其中,在整个宇宙中的迭代次数,可以确保改善平均膨胀率。在每一次迭代过程中,根据他们的膨胀率大小的分类,依靠轮盘赌机制来产生个白洞。
多元宇宙优化算法是近年来提出的一种新型的元启发式优化算法,具有参数少、结构简单、效率高、易于理解等优点,但和其他启发式算法一样,多元宇宙优化算法本身也会存在一些不足,如算法容易陷入局部最优,算法在后期运行过程中会出现收敛速度慢等问题。因此,研究改进多元宇宙优化算法的性能有着重要的理论意义和应用前景。
本文代码提供了多种测试函数进行验证,可自行更换
MVO算法逻辑介绍:
多元宇宙优化算法利用白洞和虫洞的概念来探索搜索空间,相反,虫洞在多元宇宙优化算法中协助开发搜索空间。假设每个解都是一个宇宙,每个解中的变量都是一个宇宙中的对象。在解决优化问题过程中,以下规则被应用到多元宇宙优化算法中:物体是可以通过白洞、黑洞隧道在不同的宇宙之间移动。当白洞,黑洞隧道之间建立两个宇宙,宇宙有一个膨胀率,利用具有较高膨胀率的宇宙有白洞,具有较低膨胀率的宇宙被认为有黑洞,宇宙中的粒子通过虫洞从白洞向黑洞位置转移的原理进行搜索的模拟。这个机制允许宇宙之间很容易地交换对象,不管宇宙中物质的膨胀率大小,宇宙里所有的物质都会通过虫洞随机移动,到达最佳宇宙的位置。其中,在整个宇宙中的迭代次数,可以确保改善平均膨胀率。在每一次迭代过程中,根据他们的膨胀率大小的分类,依靠轮盘赌机制来产生个白洞。白洞黑洞虫洞示意图:
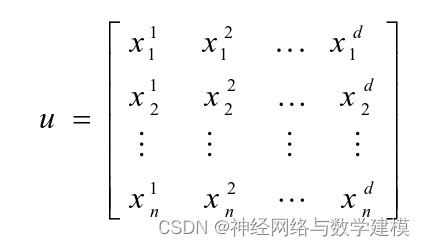
算法个体的构成如下:
其中d是变量的数量,n是宇宙的个数(候选解)。
MVO算法流程:
Step1.初始化控制参数:宇宙个数N,参数WEP,TDR,阈值H和最大迭代次数iterMax;
Step2.初始化宇宙群,寻找当前宇宙黑洞及其位置,并计算其适应度值;
Step3.按Step2所得的计算值,初始化最优值和最优记录点。
Step4.所有个体由白洞从虫洞向黑洞转移聚集。以当前最优宇宙位置点为中心,按照转移聚集规则产生新最优位置的点,替换原来的点。
Step5.计算各点的适应度,记录最优值和最优宇宙点。
Step6.黑洞个体更新。设置WEP,如果2rWEP且更新后黑洞个体适应度值比原来更优,则按照更新公式(2.3)更新个体,否则不更新。
Step7.记录最优值和最优点。
Step8.对整个宇宙群体进行评价,并分析结果。
Step9.迭代次数加1,若迭代次数小于指定次数则转Step4,否则转Step10。
Step10.若满足算法的结束前提条件则输出最优解并结束,否则继续执行步骤Step4。
多目标MVO算法介绍:
为了解决多目标优化问题,MirjaliliS.等人又提出了多目标多元宇宙算法(Multi Objective Multi-Verse Optimizer,MOMVO)(MirjaliliS.,2017)。多目标多元宇宙算法其为多元宇宙算法的多目标版本,为了开发MVO的多目标版本,首先将存档机制集成到MVO中。MOMVO的档案存储迄今为止获得的最佳非支配解的存储库。MOMVO中的搜索机制与MVO非常相似,其中使用白洞、黑洞和虫洞改进了解决方案。为了从存档中选择合适的解以在各个解之间建立隧道,本文采用了领导者选择机制。在这种方法中,首先选择档案中每个解之间的拥挤距离,并将邻域中的解数量作为覆盖或多样性的度量。MOMVO需要从档案中群体数目较少的区域选择带有轮盘赌的解,以改善档案中解在所有目标中的分布,其选择概率公式为:
式中:c大于1的常数,Ni为第i个解其附近所有解的个数。
多元宇宙的存档只能够容纳有限数量的非支配解,并且在优化过程中,多元宇宙的存档会存满,极有可能遗漏关键解。因此,算法应该有一种从存档中删除不需要的解的机制。不受欢迎的解是具有许多相邻解的解,因此本文要求存档丢弃此类解。利用上式的倒数式给那些被MOMVO算法遗弃的不受欢迎的解设置更高的被丢弃概率。
使用上述算子,MOMVO算法能够将帕累托最优解存储在存档中,并在迭代过程中对其进行改进。当以类似于中的方式将解决方案比较和添加到存档时,此算法遵循以下原则:
1如果一个新的解决方案支配了档案中的任何解决方案,它应该立即被它们替换。
2如果一个新的解决方案没有支配档案中的一个解决方案,它应该被丢弃并且不允许进入存档。
3如果一个解决方案相对于档案中的所有解决方案都是非支配的,则应将其添加到档案中。
如果存档已满,则应删除不需要的解决方案,新的非支配解决方案应进入存档。
为了比较MOMVO中的所有解,使用了帕累托最优和帕累托最优解的概念。这是因为在多目标搜索空间中,解决方案无法与关系算子进行比较。
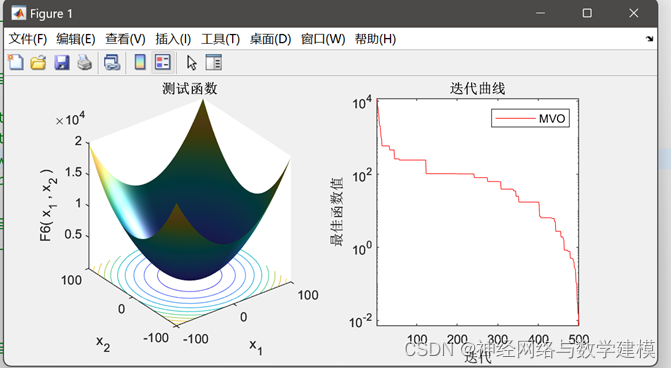
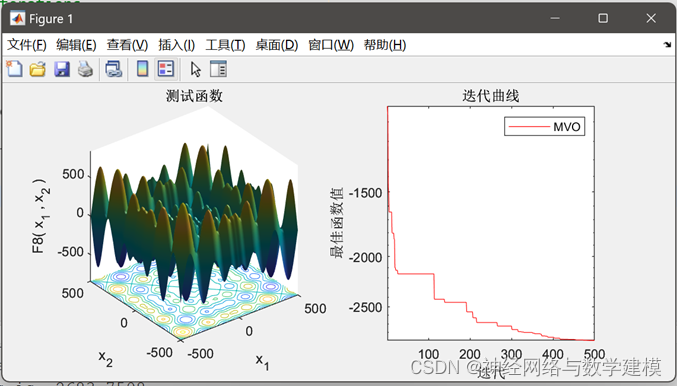
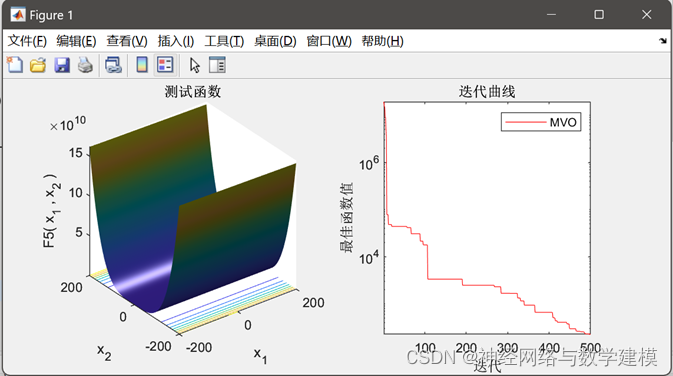
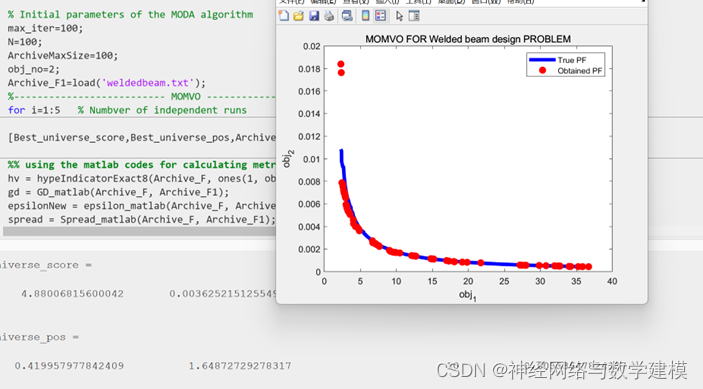
Matlab代码运行效果展示:
1. MVO