补题链接

A. Milya and Two Arrays

 思路：题意还是比较好理解，分析的话我加了一点猜的成分，对a，b数组的种类和相加小于4就不行，蒋老师的乘完后小于等于2也合理。

AC代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{
    int n, m, k;
    cin >> n;
    auto check = [&]() ->int
    {
        set<int> s;
        for (int i = 0; i<n; i++){
            int x; cin >> x;
            s.insert(x);
        }
        return s.size();
    };
    if (check()+check() > 3) cout << "YES" << endl;
    else cout << "NO" << endl;
    
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;  cin >> t;
    while (t--)
    {
        solve();
    }
    
    return 0;
}

B. Cost of the Array

 思路：这道题有点贪心在里面。

想要最小的代价，那从最小的代价为1开始做打算，怎样来计算1呢，当为前n-k+2个(不包含第一个)里面存在不为1，则分成的k块的第2块为此块，能使代价为最小1.

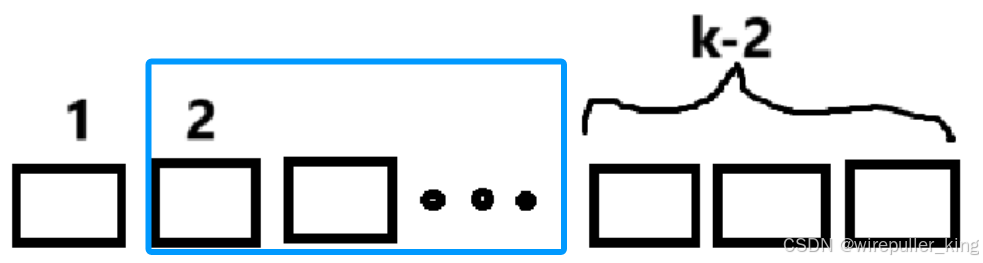
此外，想让代价最大，就得当k等于n，并且每偶数块是从1开始的递增。

因此我们可以来完善第一部分，当k不等于n时，代价不为1的话，就说明蓝色部分全为1，因为k小于n，所以第二位与第三位肯定是1，可以结合在一起使得最小的代价为2（除了当n=3,k=2），当 n=3,k=2：1 1 2，可以组成[[1],[1],[2]]，则数组B为[1, 0],代价为2，综上整合一下为AC代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define vi vector<int>
void solve()
{
    int n, m, k;
    cin >> n >> k;
    vi a(n);
    for (auto &it : a) cin >> it;
    if (k == n){
        for (int i = 1; i<n; i+=2){
            if (a[i]*2 != i+1){
                cout << (i+1)/2 << endl;
                return ;
            }
        }
        cout << k/2+1 << endl;
    }
    else {
        for (int i = 1; i<=n-k+1; i++){
            if (a[i] != 1){
                cout << 1 << endl;
                return ;
            }
        }
        cout << 2 << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    
    return 0;
}