LoRETTA：低秩经济张量训练自适应，用于大型语言模型的超低参数微调

paper是加州大学圣巴巴拉分校发表在NAACL 2024的工作

paper title：LoRETTA: Low-Rank Economic Tensor-Train Adaptation for Ultra-Low-Parameter Fine-Tuning of Large Language Models

Code地址:https://github.com/yifanycc/loretta

Abstract

为了在保持模型性能的同时实现计算效率高的微调，提出了各种参数高效微调 (PEFT) 技术。然而，随着大型语言模型 (LLM) 的快速部署，现有的 PEFT 方法仍然受到可训练参数数量不断增加的限制。为了应对这一挑战，我们提出了 LoRETTA，这是一个超参数高效框架，可通过张量训练分解显着减少可训练参数。 具体来说，我们提出了两种方法，分别名为 LoRETTAadp 和 LoRETTArep。前者采用张量化适配器，为 LLM 的微调提供了一种高性能但轻量级的方法。后者强调通过使用一组小张量因子的权重参数化进行微调。LoRETTA 在 LLaMA-2-7B 模型上实现了与大多数广泛使用的 PEFT 方法相当或更好的性能，参数减少了 100 倍。 此外，实证结果表明，所提方法有效提升了训练效率，具有更好的多任务学习性能，增强了抗过拟合能力。

1 Introduction

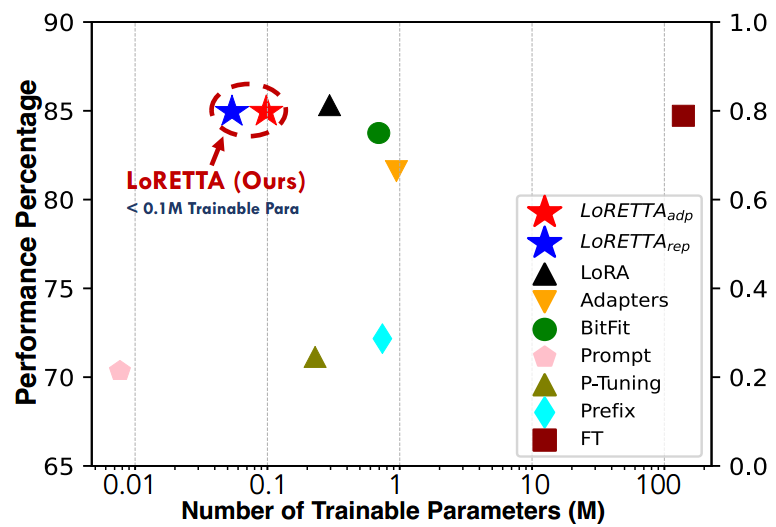
图 1：DeBERTa-Base 上的性能与可训练参数，展示了各种 GLUE 任务中参数效率和性能之间的关系。

BERT 和 LLaMA 系列（Devlin 等人，2018 年；Touvron 等人，2023 年；Floridi 和 Chiriatti，2020 年）代表了大型语言模型 (LLM) 的主流范式，在从对话系统到问答、摘要和翻译等各种应用中展示了卓越的任务泛化能力。 虽然 LLM 表现出遵循指令和以最少的上下文输入学习任务解决方案的熟练程度，但可以通过微调技术进一步提高其准确性。

由于 LLM 模型大小快速增长导致全模型微调变得不可行，人们对模型压缩和参数高效微调 (PEFT) 的兴趣日益浓厚 (Hu et al, 2023; Cheng et al, 2023c)。 PEFT 方法通过仅修改参数子集来微调 LLM。该概念最初是在 (Houlsby et al, 2019) 中探索的，它提出了 Adapters 方法将可训练模块注入 Transformer 编码器。基于这一概念，LoRA 方法 (Hu et al, 2021) 在自注意力块中的线性投影层权重上添加了低秩更新矩阵。 这两类方法实现了与全模型微调相似甚至更好的性能，但仍然会产生大量可训练参数。 以LLaMA-2-70B模型为例，LoRA需要更新超过1600万个参数，这个数字甚至比一些BERT模型的总参数还要多。

相比之下，其他方法（例如前缀调整（Li and Liang，2021）和即时调整（Lesteret al，2021））将可训练的 token 引入基础模型的输入层或隐藏层，显着减少了可训练参数，但可能会牺牲准确性，尤其是在小样本学习场景中（Mao et al，2022）。此外，（Aghajanyan et al，2020）通过探索内在维度，在 RoBERTa 模型上仅用 200∼800 个参数就实现了大约 90% 的完整微调性能，这远少于 LoRA 方法所需的 0.3 百万个参数（Hu et al，2021）。尽管 LoRA 能够胜过全模型微调，但其可训练参数的数量仍然太高，这促使我们探索更经济、更高效的高性能 PEFT 方法。这就引出了一个问题：是否存在一种具有超低可训练参数的 PEFT 方法，其性能仍然与全模型微调相当或更好？

在本文中，我们提出了一种低秩经济张量训练适配方法（Low-Rank Economic Tensor-Train Adaptation，LoRETTA），该方法专为高效微调不同规模的大型语言模型（LLMs）而设计，且仅需极少的可训练参数。我们的方法利用张量训练（Tensor-Train, TT）格式来表示大型权重矩阵。LoRETTA 包括两个变体：LoRETTA${}_{adp}$ 和 LoRETTA${}_{\text{rep}}$。

• LoRETTA${}_{adp}$ 变体在编码器/解码器层中嵌入了张量化的适配器，在相同的可训练参数规模下，其性能优于所有当前主流的参数高效微调（PEFT）方法。
• LoRETTA${}_{\text{rep}}$ 变体是我们超高效的创新方案，仅需极少的可训练参数，占用不到 1 MB 的存储空间，同时保持可比的性能。

我们的主要贡献有以下三点：

1. 提出了 LoRETTA 方法，该方法利用张量训练格式，能够在 LLaMA-2 模型上比当前广泛使用的 PEFT 方法（如 Adapters 和 LoRA）减少高达 $100\times$ 的可训练参数。
2. 所提出的框架在各种规模的模型、任务和设置下，表现出与其他主流 PEFT 方法相当的性能，尤其是在大规模模型的生成任务中表现卓越。
3. 针对其他 PEFT 方法的存储/计算效率、抗过拟合能力、多任务学习的遗忘风险以及不同设置下的性能进行了全面的研究。

2 Background

2.1 Parameter-Efficient Fine-Tuning

除了前面提到的适配器、LoRA 和基于提示的方法外，还有各种与 PEFT 相关的工作（Li and Liang，2021；Lester 等人，2021；Hyeon-Woo 等人，2021；Liu 等人，2023），包括 BitFit 方法（Zaken 等人，2022），该方法试图通过仅微调偏差项来进一步减少可训练参数。然而，据观察，BitFit 的性能下降相当大，这在我们的实验中也有所体现。此外，像 LLaMA 这样的大型模型在模型结构中不使用任何偏差项，这使得 BitFit 方法的使用受到限制。与这些先前的方法相比，提出的 LoRETTA 高效且通用，使其适用于任何类型的语言模型，为微调提供了无缝、轻量级的即插即用解决方案。

2.2 Tensor-based Model Compression

在过去十年中，张量压缩已成为一种有前途的技术，可用于减少模型大小以及推理和训练时间（Lebedev 等人，2015 年；Kim 等人，2015 年）。 例如，（Novikov 等人，2015 年）提出了 TT 格式的概念，即用一系列张量因子表示权重矩阵。（Hawkins 等人，2022 年；Hawkins 和 Zhang，2021 年）提出了一种端到端压缩训练方法，可自动确定各种张量格式的秩。尽管取得了这些进展，但张量化方法在 LLM 微调中的应用仍然有限，这主要是由于预训练权重的复杂高秩结构。

这一趋势的一个例外是 (Liu et al, 2021) 的工作，他们提出了一种张量化微调方法，只更新部分张量因子。尽管如此，它仍然需要超过 10% 的模型参数才能进行有效的微调。 (Jie and Deng, 2023) 中的研究人员则尝试将 Vision Transformer (ViT) 的所有权重矩阵堆叠成一个权重张量，并按照 LoRA 的思路创建一个张量化更新张量。然而，它对 LLM 的适用性受到堆叠张量的极大阻碍，对于 LLaMA-2-7B 模型，这个单一变量的参数就达到了 70 亿个。

3 LoRETTA Method

PEFT 方法可以大致分为三类：适配器方法（adapters）、重参数化方法（reparameterization method）和基于提示的方法（prompt-based method）（Hu et al., 2023）。其中，基于重参数化和基于适配器的方法因在模型架构中引入了新的结构而显著增加了可训练参数的数量。

为了减少注入模块的规模，我们引入了 LoRETTA 框架，其中包括基于适配器的方法 LoRETTA${}_{adp}$ 和基于重参数化的方法 LoRETTA${}_{\text{rep}}$。后续章节将详细探讨张量化层的细节，并深入剖析 LoRETTA${}_{adp}$ 和 LoRETTA${}_{rep}$ 的结构。

3.1 Tensorized TT Layer

我们在 LoRETTA${}_{adp}$ 和 LoRETTA${}_{\text{rep}}$ 中设计了基于张量化层的模块。首先，我们将线性层中的权重矩阵重塑为张量形式，然后利用张量训练（Tensor-Train, TT）格式来减少模型参数的数量。具体来说，TT 方法（Oseledets, 2011）将一个大型张量分解为一组较小的张量因子。与传统线性层需要训练大型权重矩阵不同，我们仅在微调过程中存储和训练这些小型的 TT 因子。

因此，考虑一个输入向量为 $\mathbf{x}\in {\mathbb{R}}^N$ 的全连接层，其前向传播过程可表示为：
$$\mathbf{y}=\mathbf{W}\mathbf{x}+\mathbf{b},$$
其中，$\mathbf{W}\in {\mathbb{R}}^{M\times N}$ 为权重矩阵，$\mathbf{b}$ 为偏置向量。

在张量化层中，矩阵 $\mathbf{W}$ 首先被重塑为张量 $\mathcal{W}\in {\mathbb{R}}^{k_1\times \cdots \times k_d}$，其中 ${\prod }_{i=1}^d{k}_i=M\times N$。随后，重塑后的权重张量 $\mathcal{W}$ 可以通过张量训练（TT）格式有效表示为一组张量因子 ${\mathcal{G}}_1,\cdots ,{\mathcal{G}}_i,\cdots ,{\mathcal{G}}_d$，这些张量因子的形状为 ${\mathcal{G}}_i\in {\mathbb{R}}^{r_{i-1}\times k_i\times r_i},i\in [1,d]$。对于每个维度 $i\in [1,d]$，以及张量 $\mathcal{W}$ 在维度 $i$ 上的切片中每个可能的值 $a_i:=1,\cdots ,b_i$，在给定 TT 秩 $\left[r_0,\cdots ,r_d\right]$ 的情况下，以下关系成立：

$$\mathcal{W}\left(a_1,\cdots ,a_d\right)={\mathbf{G}}_1^{a_1}\cdots {\mathbf{G}}_i^{a_i}\cdots {\mathbf{G}}_{\mathbf{d}}^{a_d},$$

其中，$G_i^{a_i}:={\mathcal{G}}_i(:,a_i,:)\in {\mathbb{R}}^{r_{i-1}\times r_i}$。通过设置首尾的 TT 秩为 $r_0=r_d=1$，可以通过每个张量因子切片矩阵的矩阵乘法计算 $\mathcal{W}$ 中的元素值。由于矩阵 $G_i^{a_i}$ 被堆叠到张量因子 ${\mathcal{G}}_i$ 中，原始权重矩阵 $\mathbf{W}$ 也可以通过 TT 表示重写为所有张量因子的乘积形式：

$$\mathrm{TT}(\mathbf{W}):=\prod _{i=1}^d{\mathcal{G}}_i\left[r_{i-1},k_i,r_i\right],$$

其中，${\mathcal{G}}_i\left[r_{i-1},k_i,r_i\right]$ 表示第 $i$ 个张量因子 ${\mathcal{G}}_i$ 的大小为 $r_{i-1}\times k_i\times r_i$。

正如我们所见，张量化层显著减少了权重矩阵 $\mathbf{W}$ 的参数量，从原始的 $M\times N$ 降低到 ${\sum }_{i=1}^d{r}_{i-1}{k}_i{r}_i$。因此，压缩率与 TT 秩的选择密切相关。为简单起见，我们将所有秩 $r_i,\forall i\in [1,d-1]$ 固定为常数。然而，正如 (Hawkins et al., 2022) 中讨论的，在训练过程中自适应地调整秩可能会进一步提升 LoRETTA 框架的性能。在下文中，我们将详细说明如何在 LoRETTA ${}_{adp}$ 和 LoRETTA ${}_{\text{rep}}$ 方法中利用这一张量化层。

3.2 Lightweight Tensorized Adapters

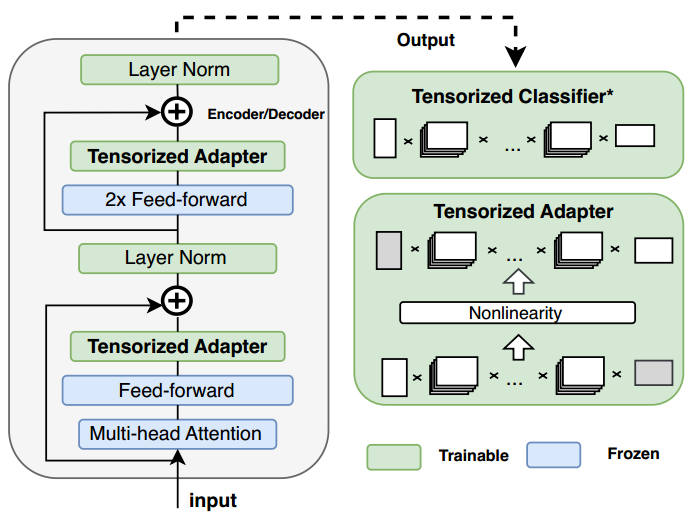
LoRETTA ${}_{\text{adp}}$ 的设计灵感来源于语言模型的超低“内在维度”（Aghajanyan et al., 2020）。这一思想已经在之前的 Adapters 和 LoRA 方法中通过瓶颈结构得以实现。然而，目前的 PEFT 方法和 (Aghajanyan et al., 2020) 探索的“内在维度”之间仍然存在较大的差距，这促使我们进一步推动这一思想的发展。在我们的方法中，我们通过注入张量化适配器（tensorized adapters）来微调大语言模型（LLMs），在超低可训练参数的情况下展现出卓越的性能。LoRETTA ${}_{\text{adp}}$ 的总体工作流程如图 2 所示。与传统 Adapters 方法利用瓶颈结构减少可训练参数不同，我们的张量化适配器通过包含两个张量化线性层和一个激活函数，实现了更高的压缩率。例如，假设模型的隐藏层大小为 768，瓶颈大小为 64。与传统 Adapters 方法在权重矩阵中需要 $2\cdot 768\cdot 64\approx 98\text{K}$ 可训练参数相比，LoRETTA ${}_{\text{adp}}$ 仅需 ${\sum }_{i=1}^6\left(5^2\cdot 8\right)=1.2\text{K}$ 个参数（假设张量形状为 $[8,8,8,8,8,8]$，TT 秩固定为 5）。受 (Houlsby et al., 2019) 的启发，我们在自注意力块（self-attention blocks）的每个注意力子层和前馈子层之后引入可训练的张量化适配器。

图 2：LoRETTA ${}_{\text{adp}}$ 在 Transformer 编码器或解码器中的架构。* 对于不同任务，张量化分类器（tensorized classifier）是可选的。在分类任务中，我们将该部分设置为可训练；而在语言建模任务中，我们冻结该部分。

可优化模块：除了对张量化适配器模块进行微调外，我们还研究了如何使层归一化和网络的最后一层可训练。从附录 B 中的观察结果可以看出，微调模型的最后一层对于分类任务至关重要。然而，在 RoBERTa 和 DeBERTa 等模型中，由于最后一层的参数数量众多，微调最后一层是一个常见的挑战。 为了解决这个问题，我们在我们的方法中对分类任务采用了张量化的最后一层，从而显著减少了可训练参数，同时保持了有效性，这在我们的实验中得到了证实。请注意，我们选择冻结语言模型任务的最后一层，因为语言模型头的参数是从预训练权重中继承的。

3.3 TT Reparameterization

接下来，我们提出了一种更紧凑的 PEFT 方法，通过用张量因子重新参数化权重矩阵，称为 LoRETTA ${}_{\text{rep}}$。这一重新参数化的思想也出现在 LoRA (Hu et al., 2021) 中，它通过线性层中的两个低秩矩阵更新权重，公式如下：
$$y=W_{0}x+\Delta Wx=W_{0}x+BAx$$
其中，$\mathbf{x}$ 和 $\mathbf{y}$ 分别表示线性层的输入和输出。设模型的隐藏大小为 $d$，$W_0\in {\mathbb{R}}^{d\times l}$ 是预训练的权重矩阵，$B\in {\mathbb{R}}^{d\times r}$ 和 $A\in {\mathbb{R}}^{r\times l}$ 是表示更新矩阵 $\Delta W$ 的低秩矩阵，其中 $r\ll \min (d,l)$ 是 LoRA 的秩参数。在原始的 LoRA 方法中，矩阵 $A$ 通过高斯分布初始化，而矩阵 $B$ 初始化为零，以确保初始时更新部分 $BA=0$。

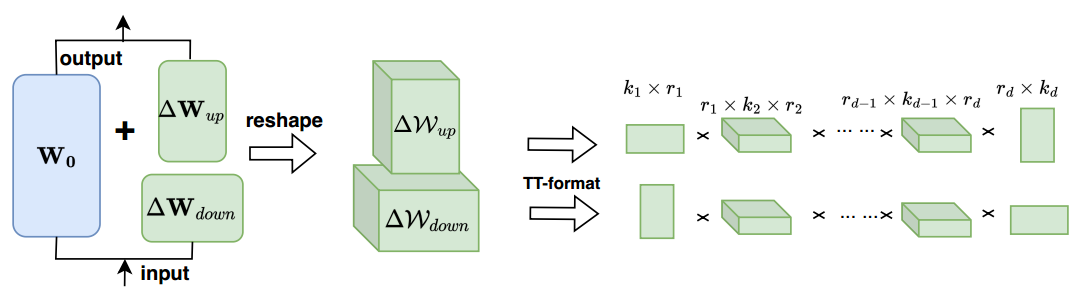
单个变压器编码器的LoRETTA ${}_{\text{rep}}$方法的架构。

然而，如引言中所述，仅通过矩阵分解对权重进行重新参数化可能无法充分利用内在维度。在此，我们提出了一种更紧凑的方式来表示更新矩阵，即利用第 3.1 节中介绍的两个无偏张量化层。这一方法的基本思想如图 3 所示。在我们的方法中，我们同样使用瓶颈结构，首先将大的更新矩阵压缩为两个小矩阵。然后，我们将这两个更新矩阵 $\Delta {\mathbf{W}}_{\text{up}}$ 和 $\Delta {\mathbf{W}}_{\text{down}}$ 重塑为形状为 $k_1\times \cdots \times k_d$ 和 $j_1\times \cdots \times j_d$ 的张量 $\Delta {\mathcal{W}}_{\text{up}}$ 和 $\Delta {\mathcal{W}}_{\text{down}}$。接着，我们将 $\Delta {\mathcal{W}}_{\text{up}}$ 和 $\Delta {\mathcal{W}}_{\text{down}}$ 转换为张量训练（TT）因子。全连接层对输入 $\mathbf{x}$ 的张量化更新过程可以表示为：
$$\begin{array}{rl}\mathbf{y}& ={\mathbf{W}}_0\mathbf{x}+\mathrm{TT}\left(\Delta {\mathbf{W}}_{\text{up}}\right)\cdot \mathrm{TT}\left(\Delta {\mathbf{W}}_{\text{down}}\right)\mathbf{x}\\ & ={\mathbf{W}}_0\mathbf{x}+\prod _{i=1}^d{\mathcal{G}}_i\prod _{i=1}^d{\mathcal{Q}}_i\mathbf{x}\end{array}$$
其中，${\mathcal{G}}_i$ 和 ${\mathcal{Q}}_i$ 分别是 $\Delta {\mathcal{W}}_{\text{up}}$ 和 $\Delta {\mathcal{W}}_{\text{down}}$ 的张量训练因子。

初始化： 如前所述，LoRA 方法以 $B=0$ 作为初始化，这使得初始模型的输出与重新参数化之前的输出保持一致。然而，我们提出的方法需要对每个张量因子进行优化。如果将某个因子初始化为零，可能会由于梯度为零的问题导致算法陷入停滞。为了解决这个问题，我们从高斯分布对所有张量因子进行初始化。接着，为了评估并减轻高斯初始化可能引入的噪声，我们通过在训练的第一个步骤中执行张量重构（Kolda and Bader, 2009），从初始化的权重矩阵中进行调整。