蜣螂优化算法(Dung beetle optimizer,DBO)是一种新型群智能优化算法,该算法是受蜣螂滚球、跳舞、觅食、偷窃和繁殖行为启发而提出的,具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2022年发表在知名SCI期刊THE JOURNAL OF SUPERCOMPUTING上。目前谷歌学术上查询被引102次。
DBO算法通过滚球、跳舞、觅食、偷窃和繁殖的过程,五个主要操作模拟了蜣螂的生存行为,最后选取最优解。
算法原理
(1)滚球行为
蜣螂在滚动的过程中利用天体导航,蜣螂滚动路径受环境影响,环境的变化也影响着蜣螂位置的改变:
式中:t为当前迭代次数; 表示第 只蜣螂在第 次迭代时的位置信息; 为(0,0.2)之间的常数,表示缺陷系数; 为(0,1)的常数; 为-1或1的自然系数; 为全局最差位置;∆x为环境变化。
(2)跳舞行为
当蜣螂遇到障碍无法继续前进时,通过跳舞行为变换方向,获得新的移动路线。使用切线函数得到新的滚动方向,在[0,π]区间值,确定新方向后,继续滚球行为: 如果角度为0,π/2,π时,蜣螂的位置不更新。
(3)繁殖行为
蜣螂将粪球滚动到安全区域后进行隐藏,合适的产卵地点对于蜣螂后代来说至关重要,提出一种边界选择策略模拟雌性蜣螂的产卵区域: 式中: 为当前局部最佳位置; , 分别为产卵区的下限和上限; 表示动态选择因子; 为最大迭代次数; , 分别为优化问题的下限和上限。
确定产卵区域后,每只雌性蜣螂每次产一枚卵。产卵的区域随迭代次数动态调整,卵球的位置也是动态变化的: 式中, 表示第 次迭代时第 个卵球的位置; , 均为1×D的独立随机向量;D为优化问题的维数。
(4)觅食行为
幼虫从卵中钻出后,需要限定最佳觅食区域引导小蜣螂觅食,最佳觅食区域的边界为: 式中: , 分别为最佳觅食区域的下限和上限; 为全局最佳位置。小蜣螂在觅食过程中位置的更新为: 式中:C1为服从正态分布的随机数;C2为(0,1)的随机数。
(5)偷窃行为
蜣螂种群中,偷窃作为一种竞争行为十分常见,偷窃蜣螂的位置更新为: 式中:S为常数;g为服从正态分布的1×D随机向量。
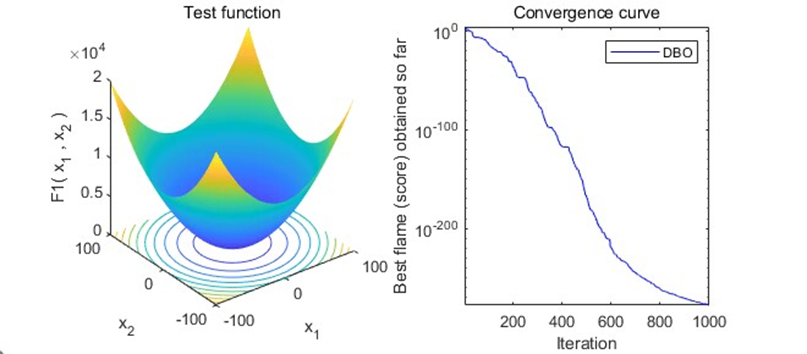
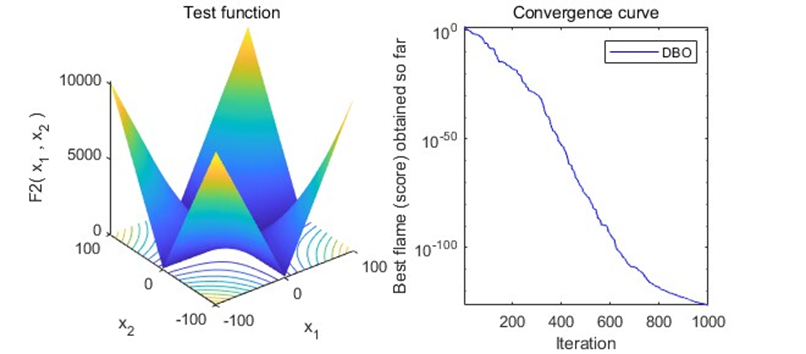
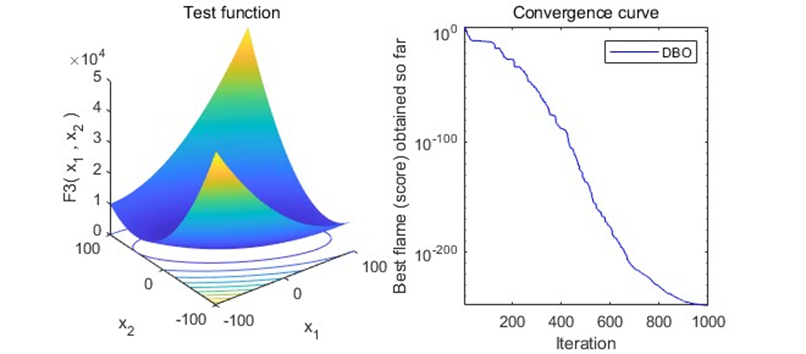
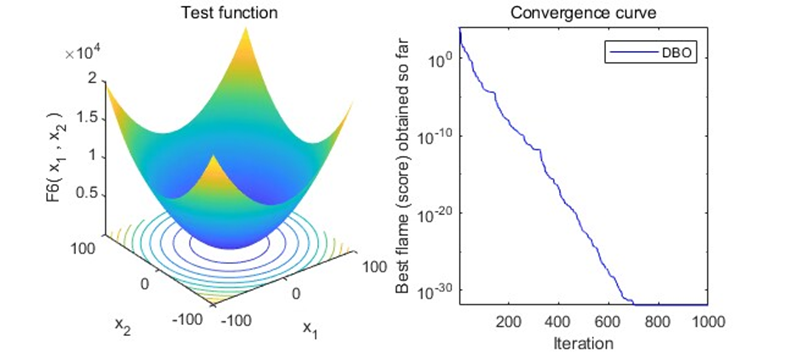
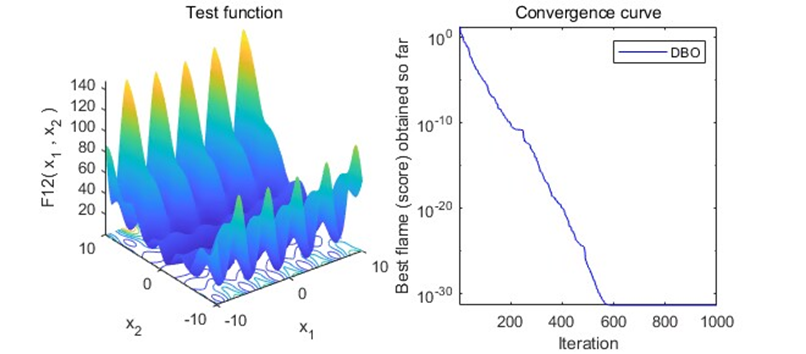
结果展示
以为CEC2005函数集为例,进行结果展示:
MATLAB核心代码
function [fMin , bestX, Convergence_curve ] = DBO(pop, M,c,d,dim,fobj )
P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( pop * P_percent ); % The population size of the producers
lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
for i = 1 : pop
x( i, : ) = lb + (ub - lb) .* rand( 1, dim );
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x;
XX=pX;
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
% Start updating the solutions.
for t = 1 : M
[fmax,B]=max(fit);
worse= x(B,:);
r2=rand(1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1 : pNum
if(r2<0.8)
r1=rand(1);
a=rand(1,1);
if (a>0.1)
a=1;
else
a=-1;
end
x( i , : ) = pX( i , :)+0.3*abs(pX(i , : )-worse)+a*0.1*(XX( i , :)); % Equation (1)
else
aaa= randperm(180,1);
if ( aaa==0 ||aaa==90 ||aaa==180 )
x( i , : ) = pX( i , :);
end
theta= aaa*pi/180;
x( i , : ) = pX( i , :)+tan(theta).*abs(pX(i , : )-XX( i , :)); % Equation (2)
end
x( i , : ) = Bounds( x(i , : ), lb, ub );
fit( i ) = fobj( x(i , : ) );
end
[ fMMin, bestII ] = min( fit ); % fMin denotes the current optimum fitness value
bestXX = x( bestII, : ); % bestXX denotes the current optimum position
R=1-t/M; %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Xnew1 = bestXX.*(1-R);
Xnew2 =bestXX.*(1+R); %%% Equation (3)
Xnew1= Bounds( Xnew1, lb, ub );
Xnew2 = Bounds( Xnew2, lb, ub );
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Xnew11 = bestX.*(1-R);
Xnew22 =bestX.*(1+R); %%% Equation (5)
Xnew11= Bounds( Xnew11, lb, ub );
Xnew22 = Bounds( Xnew22, lb, ub );
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = ( pNum + 1 ) :12 % Equation (4)
x( i, : )=bestXX+((rand(1,dim)).*(pX( i , : )-Xnew1)+(rand(1,dim)).*(pX( i , : )-Xnew2));
x(i, : ) = Bounds( x(i, : ), Xnew1, Xnew2 );
fit(i ) = fobj( x(i,:) ) ;
end
for i = 13: 19 % Equation (6)
x( i, : )=pX( i , : )+((randn(1)).*(pX( i , : )-Xnew11)+((rand(1,dim)).*(pX( i , : )-Xnew22)));
x(i, : ) = Bounds( x(i, : ),lb, ub);
fit(i ) = fobj( x(i,:) ) ;
end
for j = 20 : pop % Equation (7)
x( j,: )=bestX+randn(1,dim).*((abs(( pX(j,: )-bestXX)))+(abs(( pX(j,: )-bestX))))./2;
x(j, : ) = Bounds( x(j, : ), lb, ub );
fit(j ) = fobj( x(j,:) ) ;
end
% Update the individual's best fitness vlaue and the global best fitness value
XX=pX;
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
if( pFit( i ) < fMin )
% fMin= pFit( i );
fMin= pFit( i );
bestX = pX( i, : );
% a(i)=fMin;
end
end
Convergence_curve(t)=fMin;
end
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
temp = s;
I = temp < Lb;
temp(I) = Lb(I);
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;
function S = Boundss( SS, LLb, UUb)
% Apply the lower bound vector
temp = SS;
I = temp < LLb;
temp(I) = LLb(I);
% Apply the upper bound vector
J = temp > UUb;
temp(J) = UUb(J);
% Update this new move
S = temp;参考文献
[1] Xue J, Shen B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization[J]. The Journal of Supercomputing, 2023, 79(7): 7305-7336.
完整代码获取方式:后台回复关键字:
TGDM990