目录
第四章 图像处理原理与应用
2 图像预处理技术
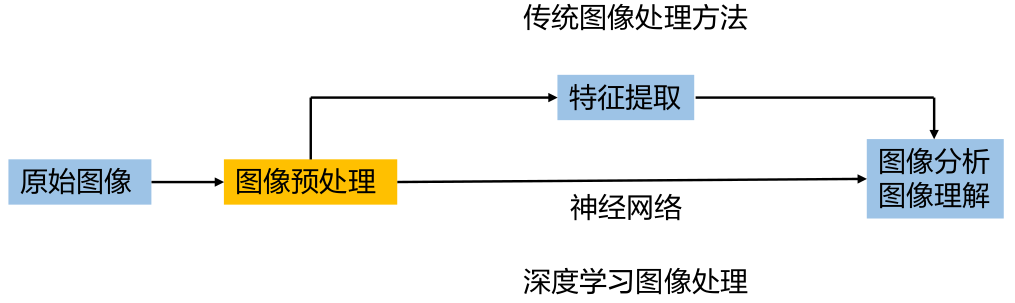
■ 图像处理的一般流程
图像处理的一般流程:
传统图像处理算法中图像预处理的目的:是消除图像中无关的信息,恢复有用的真实信息,增强有关信息的可检测性、最大限度地简化数据,从而改进特征提取、图像分割、匹配和识别的可靠性。
图像预处理包括:灰度变换,几何矫正,图像增强,图像滤波等操作。
■ 灰度变换
▲ 灰度变换
图像灰度变换是将原始图像中每一个点的灰度值,按照特定映射函数,变换为另一个灰度值。
灰度变换是对每一个像素点单独的操作,记录像素点的原始值为S,灰度变换的映射函数为T(s) ,变换后像素点的值为d,即:d=T(s)
选择不同的灰度变换函数,可以实现增强图像视觉效果的目的。对于灰度级为 L的图像,映射函数是一个将 [0, L−1] 的输入值映射到 [0, L−1] 的输出值的函数。可以将映射函数的图形绘制出来,表示灰度变换的效果。
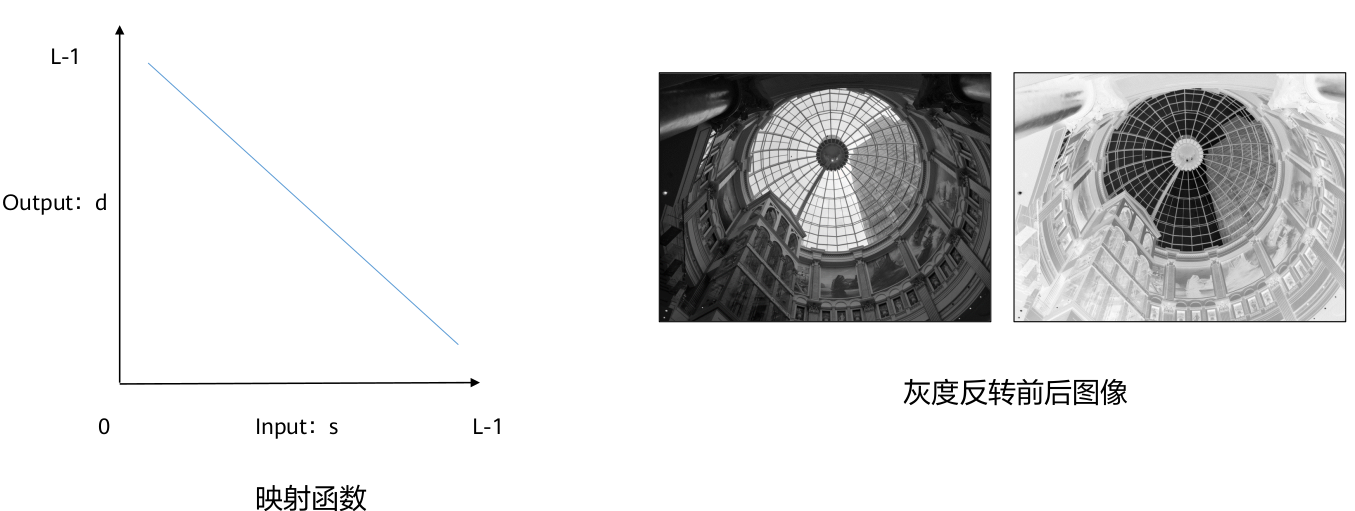
▲ 反转
图像反转:将原图灰度值反转的操作,简单说就是将黑色变为白色,白色变为黑色。
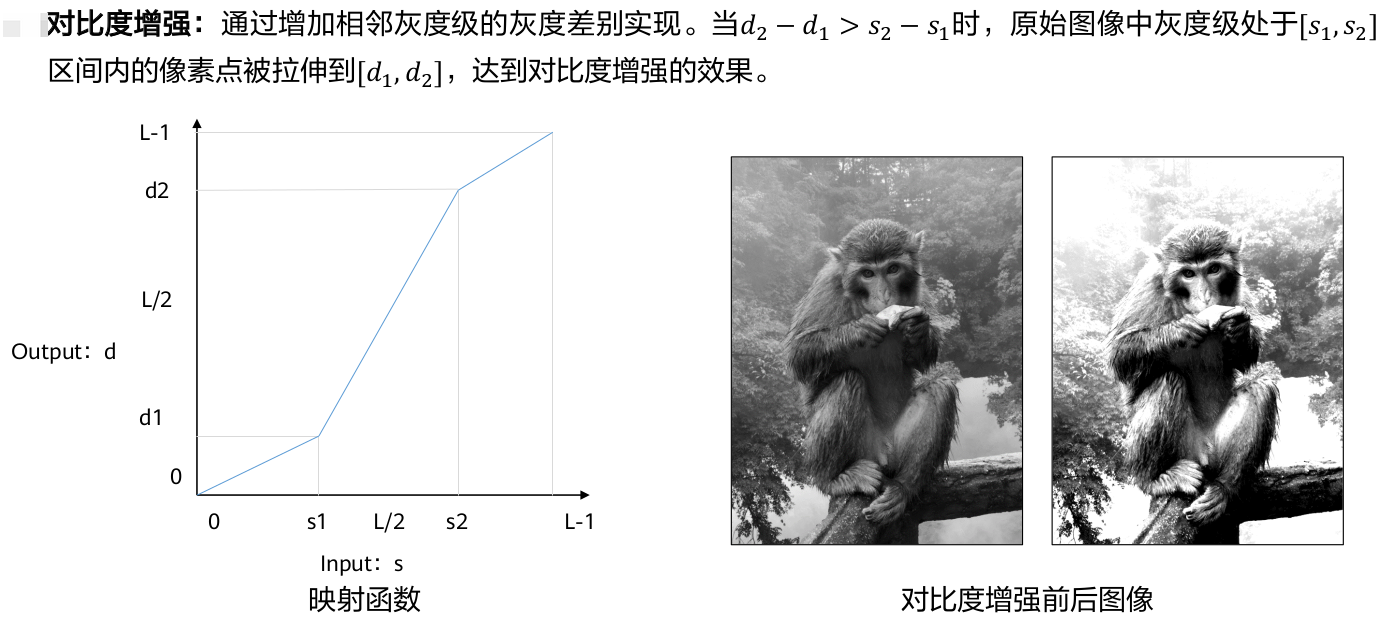
▲ 对比度增强
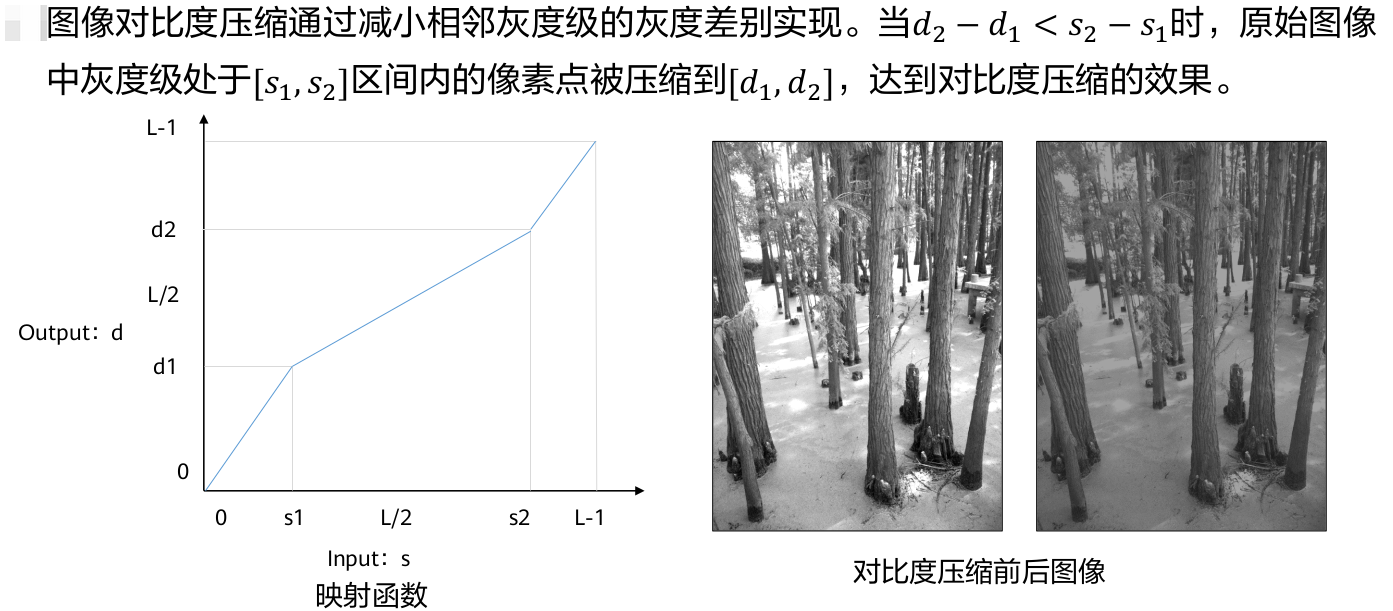
▲ 对比度压缩
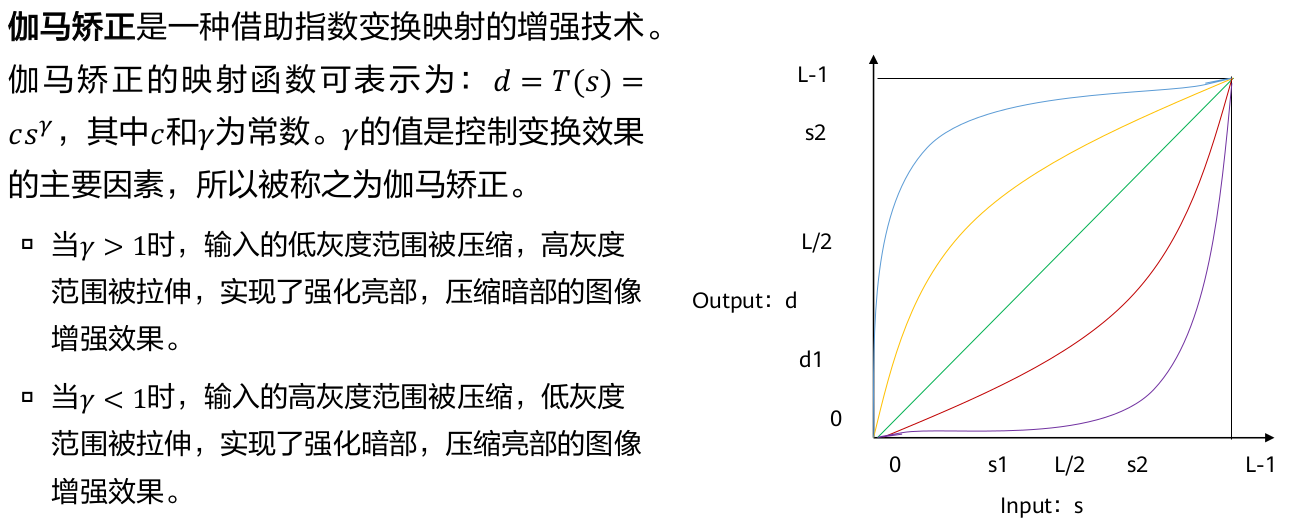
▲ 伽马矫正
γ的值距离 1 越远,伽马矫正的变换强度越大。
▲ 直方图
直方图:反映的是一幅图像中各灰度级像素出现的频率,反映了图像灰度分布的情况。
直方图的绘制:以灰度级i为横坐标,纵坐标为灰度级出现的频率Vi =ni/n,
ni为灰度级为i的像素个数,n 为像素总个数,绘制频率同灰度级的关系图。
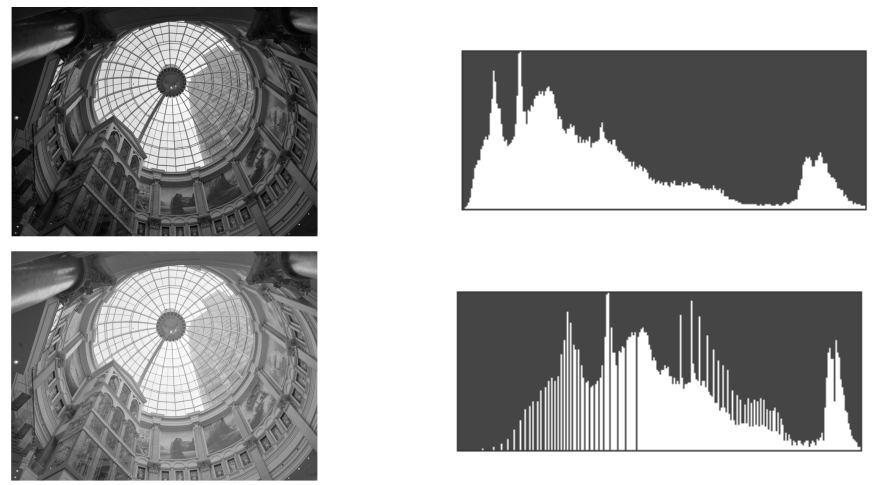
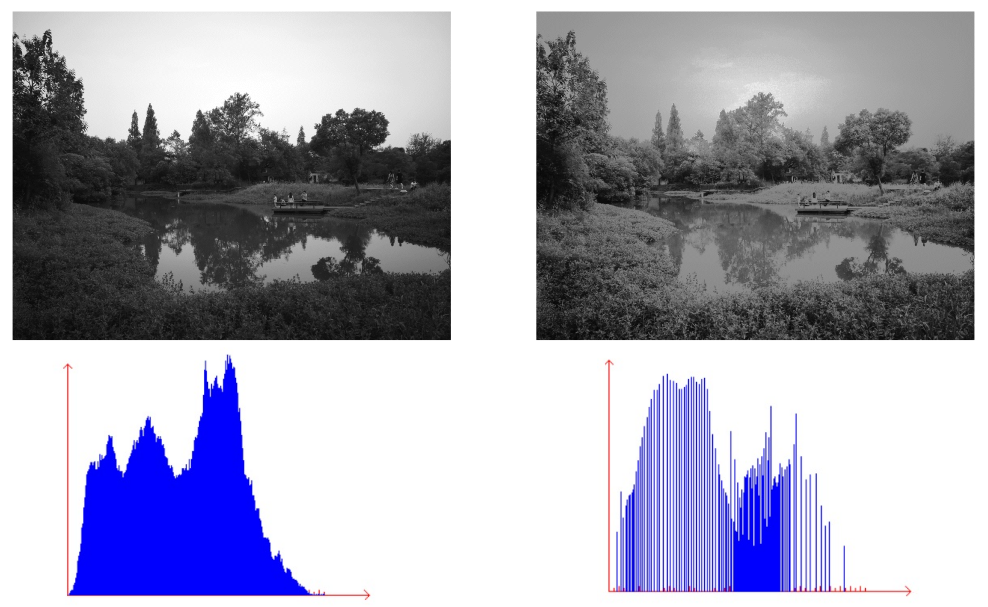
◎ 灰度图像直方图
以下是两幅灰度图像的直方图,直方图的形状能反映图像的视觉效果。
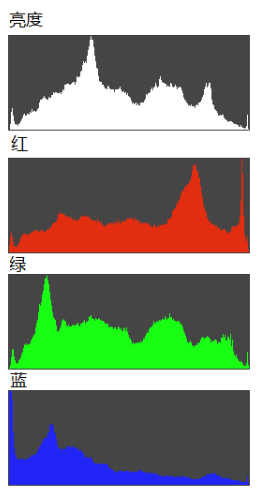
◎ 彩色图像直方图
对于彩色图像,可以对不同的通道分别绘制直方图。
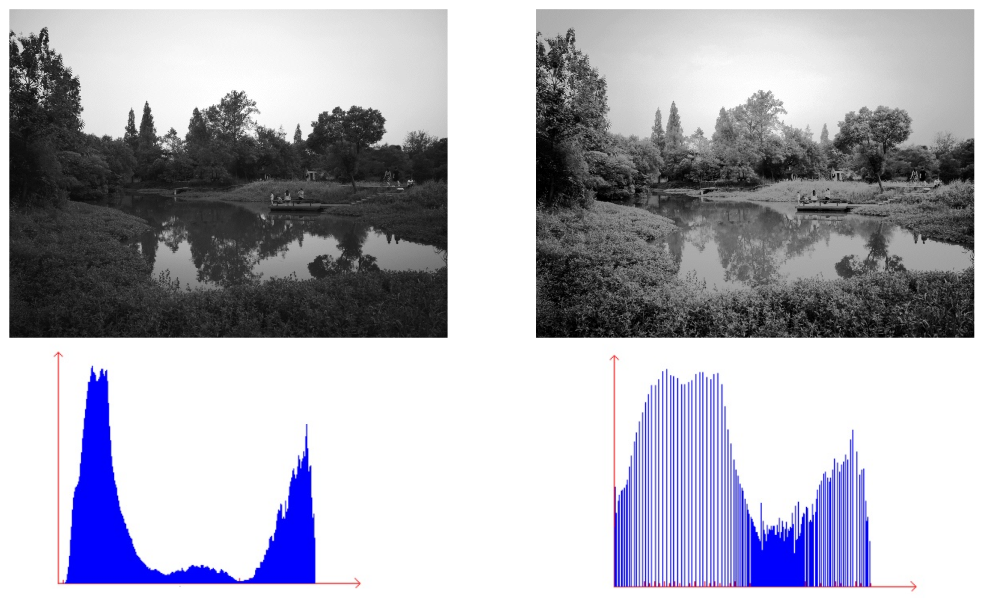
◎ 直方图均衡化
直方图均衡化:调整原始图像的直方图,即灰度概率分布图,使之呈均衡分布的样式,以达到灰度级均衡的效果,可以有效增强图像的整体对比度。直方图均衡化能够自动地计算变换函数,并产生有均衡直方图的输出图像。能够有效增强改善图像过暗、过亮和细节不清晰的问题。在常用的图像处理库中,直方图操作都有API(cv2.equalizeHist(img))直接调用实现。
整图处理。
◎ 直方图规定化
直方图均衡化总是得到全局均衡化的输出图像,但实际应用中经常需要对某些特定的灰度区间进行增强,如提升暗部或增强亮部。使用直方图规定化的方法可以按需要灵活地对直方图的分布进行调整。这种定制化调整是直方图规定化的特点。
直方图规定化的方法也是调整原始图像的直方图,使得其概率分布逼近目标直方图的概率分布。使用直方图规定化的方法,需先根据经验知识,计算最合适的目标直方图,与原始图像一起作为输入,输出规定化后的图像,从而达到特定的图像增强效果。
▲ 空间滤波
空间滤波:是一种局部处理方式,像素p的输出值由输入图像中像素p及其邻域 N 中的像素值确定。
计算方法:将邻域 N 的像素值和一个与邻域同样尺寸的子图像进行模板运算。子图像被称为模板、核或滤波器。
模板:可看作一副尺寸为 n × n 的小图像 W , n 一般取奇数称为模板的尺寸,每个位置上的值w 被称为权重。在进行计算时,将模板的中心和像素 p 对齐,选取原始图像中和模板相同范围的邻域 N的像素值作为输入。 常用的模板运算有模板卷积和模板排序。
◎ 模板卷积
模板卷积:指用模板与需处理图像空间进行卷积的运算过程。卷积过程不能原地完成,所以输出结果要使用另一幅图像。
◎ 模板排序
模板排序:用模板来提取待处理图像中与模板同尺寸的图像子集, 将邻域 N 的像素值进行排序,选择特定次序的灰度值,作为像素p 位置的输出值,如最大值、最小值、中位数等。
◎ 均值滤波
均值滤波:模板权重都为 1 的滤波器,它将像素的邻域平均值作为输出结果。均值滤波有图像平滑、去除噪声的作用,但随着模板尺寸的增加图像会变得模糊,经常用于图像模糊化。
◎ 高斯滤波
高斯滤波:模板根据高斯分布来确定模板系数,接近中心的权重比边缘大。可以减少由模板尺寸增加所造成的图像模糊。
◎ 中值滤波
中值滤波:将邻域内像素排序后的中位数值输出以代替原像素值,属于模板排序运算的滤波器。它不仅能实现降噪,而且保留了原始图像的锐度,不会修改原始图像的灰度值。
中值滤波的使用非常普遍,它对椒盐噪声( Salt & Pepper Noise )的抑制效果很好,在抑制随机噪声的同时能有效保护图像边缘信息。但中值滤波是一种非线性变化,它可能会破坏像素点的线性关系,不适用于点、线等细节较多的图像或高精度的图像。
◎ 图像锐化
锐化处理的主要目的:突出图像中的边缘、轮廓线和图像细节。
图像锐化实现:将求取的边缘按照一定系数比例叠加到原始图像上,即可实现对图像的锐化操作。
例如使用 Laplacian 梯度算子作为锐化操作的模板,其中 A 是大于等于 1 的系数。
◎ 边缘检测
图像边缘是图像的最基本特征,是图像分割所依赖的最重要特征。
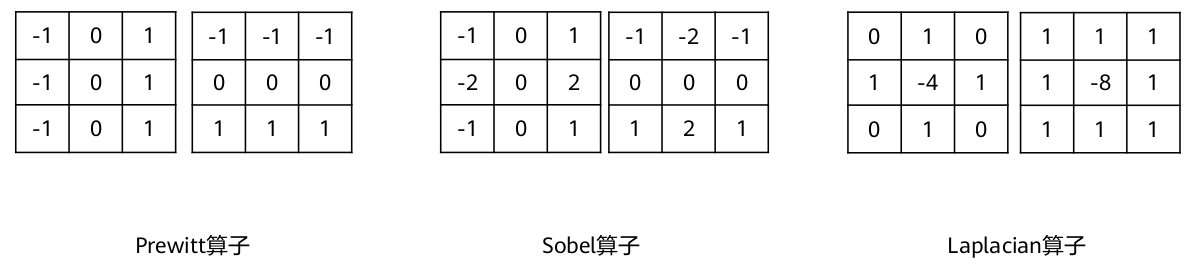
边缘检测算子主要有:
一阶梯度: Prewitt 梯度算子、 Sobel 梯度算子。
二阶梯度: Laplacian 梯度算子。
■ 坐标变换
图像的坐标变换又称为图像的几何计算,常见的基本变换包括:图像的平移、旋转、镜像、缩放等。
图像的坐标变换的实现方式:通过坐标向量和变换矩阵相乘实现。
▲ 平移
▲ 镜像
▲ 旋转
▲缩放
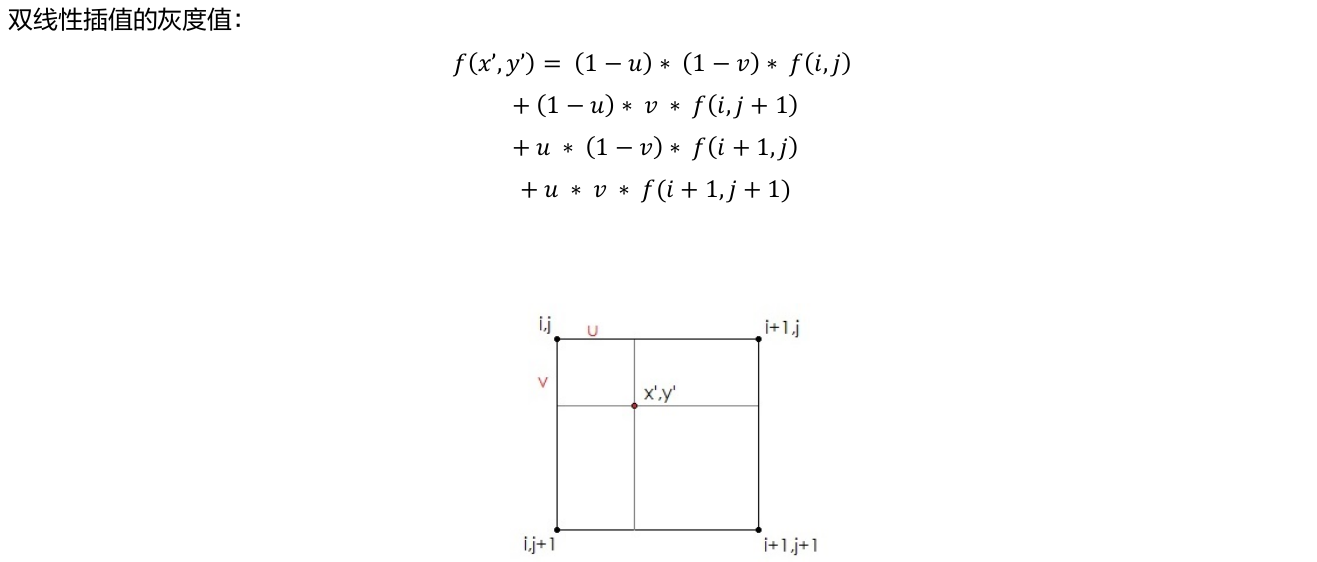
▲ 插值
最邻近插值与双线性插值
▲ 仿射变换
在二维平面对图像进行线性坐标变换的方法,包括了图像平移、缩放、旋转、镜像等。仿射变换保留了图像中的 “平行性”和“平直性”,即仿射变换后直线和平行线仍然保持是直线和平行线。变换公式为:
▲ 彩色图像处理
彩色图像的每个像素点都有多个通道,例如 RGB 图像中每个像素有 (r, g, b) 三个值。对于多通道图像的处理,有两种思路:
①将每个像素看做一个多维度的向量,直接用向量的表达方式进行图像处理;
②将其看作多幅单通道图像的组合体,处理过程中对每个通道的图像单独处理,最后再将每个通道的结果合成为一副彩色图像。
单通道处理:
数字图像处理中,最通用的颜色空间是 RGB 颜色空间,在处理彩色图像时,可以将 R , G , B 三通道进行分离,对三个通道分别进行前面介绍的预处理操作。
色调增强:
由于人眼对 HSV 空间的三个分量的感受是独立的,可以对 HSV 单独的分量图进行处理达到图像增强的目的。
对 HSV 空间的 H 分量进行处理可以实现对图像色调的增强。
色相的调整通常在 H 原始值上加上一个小的偏移量,使其在色相环上有小角度的调整。调整后,图像的色调会变为冷色或者暖色;色相 H 的值对应的是一个角度,并且在色相环上循环。所以色相的修正可能会造成颜色的失真。
饱和度增强:
对 HSV 空间的 S 分量进行处理可以实现图像饱和度的增强。饱和度的调整通常是在 S 原始值上乘以一个修正系数。
修正系数大于 1 ,会增加饱和度,使图像的色彩更鲜明。
修正系数小于 1 ,会减小饱和度,使图像看起来比较平淡。
亮度增强:
对 HSV 空间的 V 分量进行处理可以实现图像亮度的增强。
直接将彩色图像灰度化,也可以得到代表图像亮度的灰度图,计算量比 HSV 颜色空间变换低,但在 HSV 空间中进行亮度增强处理可以得到增强后的彩色图像。
■ 图像预处理在深度学习中的作用
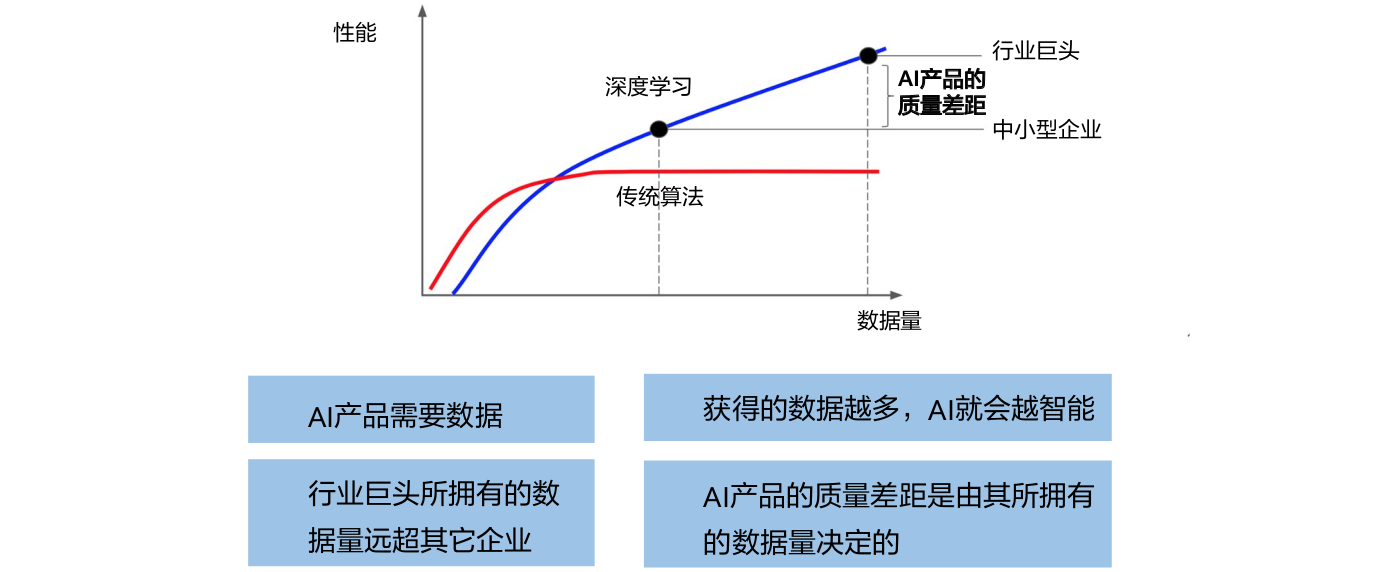
▲ 数据的重要性
▲ 数据增强
数据增强:即增加训练数据样本。防止过拟合最有效的方法是增加训练样本,足够多的数据可以让模型看见尽可能多的例外情况并不断修正自己,从而效果更好。数据增强是一个省时有效的方法,在不同领域有不同的实现方法:
在图像处理领域常用的方法是将图片进行旋转、平移缩放等(图片变换的前提是通过变换不能改变图片所属类别,例如手写数字识别,类别6和9进行旋转后容易改变类目)。
语音识别中对输入数据添加随机噪声。
NLP中常用思路是进行近义词替换。
说明:本文内容来源于网络,仅作为学习用途,如有侵权,请联系作者删除。