ROS-Navigation包中DWA算法研究一（DWA算法介绍）

一、DWA算法介绍

DWA算法全称为：Dynamic Window Approach，中文为动态窗口法，其原理主要是在速度空间（v,w）中采样多组速度，并模拟这些速度在一定时间内的运动轨迹，再通过一个评价函数对这些轨迹打分，最优的速度被选择出来发送给下位机。
动态窗口的意思是
根据移动机器人的加减速性能限定速度采样空间在一个可行的动态范围呢。

二、DWA算法推导

推导过程请参考：
https://blog.csdn.net/heyijia0327/article/details/44983551添加链接描述

2.1、建立模型

在上述文章中建立了两种模型：

1、模型一

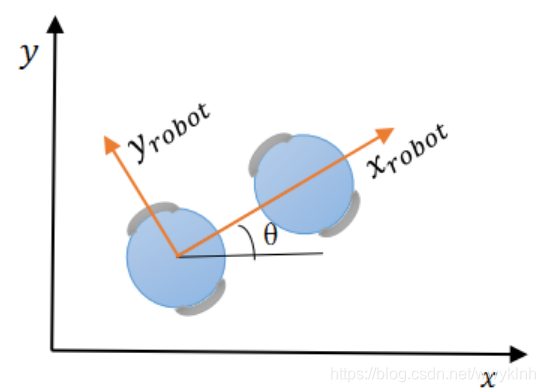
机器人为全向运动，即机器人可以在x，y方向运动，也可以旋转。
则在Δt时间呢，机器人运动轨迹如下：
$\bullet x=x+v_{x}\Delta t\cos (\theta_{t} )-v_{y}\Delta t\sin (\theta_{t} )$
$\bullet y=y+v_{x}\Delta t\sin (\theta_{t} )-v_{y}\Delta t\cos (\theta_{t} )$
$\bullet \theta _{t}=\theta _{t}+w\Delta t$
其中x，y为世界坐标系， $v_{x}$ 、 $v_{y}$ 为车辆坐标系，具体如下图所示：
在这里插入图片描述

2、模型二

在模型一中是假设机器人在相邻时间段内的轨迹是直线，模型二采用圆弧代替。
假设机器人不是全向机器人，它做圆弧的半径为：
$r=\frac{v}{w}$
当旋转w不为0时，机器人的坐标为：
$\bullet x=x-\frac{v}{w}\sin (\theta _{t})+\frac{v}{w}\sin (\theta _{t}+w\Delta t)$
$\bullet y=y-\frac{v}{w}\cos (\theta _{t})-\frac{v}{w}\cos (\theta _{t}+w\Delta t)$
$\bullet \theta _{t}=\theta _{t}+w\Delta t$

2.2、速度采样

根据机器人的轨迹模型，根据速度就可以推算出轨迹，因此只需要采样很多速度，推算轨迹，然后评价这些轨迹好不好即可。
在机器人速度（v,w）的二维空间里存在无限种可能，但是机器人本身和环境的限制可以将机器人的速度限制在一定范围内。主要受以下条件限制：

一、移动机器人自身最大最小速度限制

$V_{m}=\left \{v\in \left [ v_{min},v_{max}\right ],w\in \left [ w_{min},w_{max}\right ]\right \}$

二、移动机器人受电机性能影响

由于电机扭矩有限，因此存在最大加减速，因此存在一个动态窗口，在窗口内的速度就是机器人可以达到的最大速度。
$V_{d}=\left \{(v,w)|\begin{matrix} v\in \left [ v_{c}-\dot{v}_{b}\Delta t,v_{c}+\dot{v}_{a}\Delta t\right ]\\ w\in \left [ w_{c}-\dot{w}_{b}\Delta t,w_{c}+\dot{w}_{a}\Delta t\right ] \end{matrix}\right \}\dot{v}$
其中， $v_{c}$ , $w_{c}$ 是机器人的当前速度， $\dot{v}_{b}$ 、 $\dot{v}_{a}$ 、 $\dot{w}_{b}$ 、 $\dot{w}_{a}$ 分别对应最大加速度，最大减速度。

三、基于移动机器人安全考虑

为了能在碰到障碍物之前停下，因此在最大减速度范围下，速度有一个范围：
$V_{a}=\left \{(v,w)|v\leq \sqrt{2\cdot dist(v,w)\cdot \dot{v}_{b}},w\leq \sqrt{2\cdot dist(v,w)\cdot \dot{w}_{b}}\right \}$
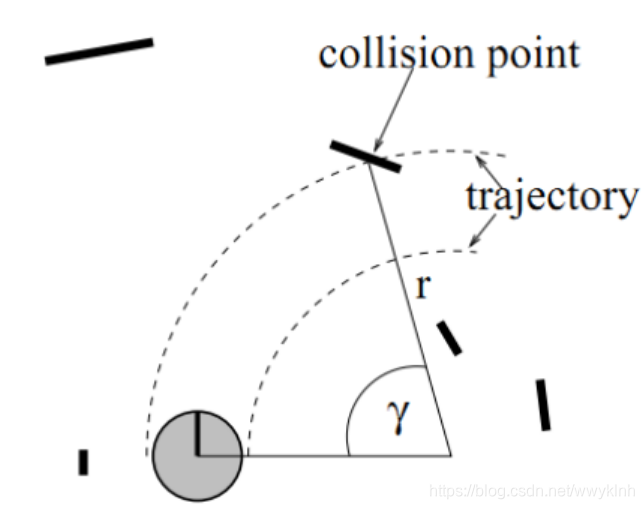
其中， $d i s t (v, w)$ 为速度 $(v, w)$ 对应轨迹上离障碍物最近的距离，如下图所示：
在这里插入图片描述注意：这个条件需要模拟出轨迹，找到障碍物位置之后，计算出障碍物到轨迹的距离，然后看当前速度能否在碰到障碍物之前停下，如果能停下，这个速度就是可接受的，否则，这对速度就得抛弃。

2.3、评价函数

在采样的速度组中，有若干组轨迹是可行的，因此采用评价函数的方式对每条轨迹进行评价，采用的评价函数如下:
$G(v,w)=\sigma (\alpha \cdot heading(v,w)+\beta \cdot dist(v,w)+\gamma \cdot velocity(v,w))$

一、方位角评价函数

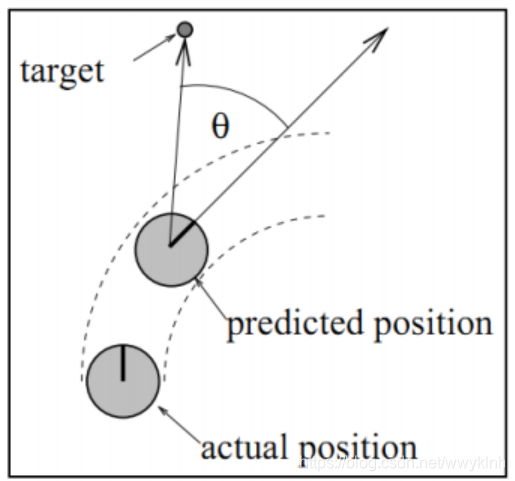
$h e a d i n g (v, w)$ 是用来评价机器人在当前设定的采样速度下，达到模拟轨迹末端时的朝向和目标之间的角度差距，如下图所示：
在这里插入图片描述

二、空隙

$d i s t (v, w)$ 代表机器人在当前轨迹上与最近的障碍物之间的距离。如果这条轨迹上没有障碍物，那就将其设定为一个常数。

三、速度

$v e l o c i t y (v, w)$ 用来评价当前轨迹的速度大小。

四、平滑处理

上面三个部分计算出来后，每一个需要进行归一化处理，之后再相加。
即每一项除以每一项的总和：
$normal_{-}head(i)=\frac{head(i)}{\sum_{n}^{i=1}head(i)}$
$normal_{-}dist(i)=\frac{dist(i)}{\sum_{n}^{i=1}dist(i)}$
$normal_{-}velocity(i)=\frac{velocity(i)}{\sum_{n}^{i=1}velocity(i)}$
其中，n为采样的所有轨迹点，i为待评价的当前轨迹点。

三、DWA算法实现

程序中代码注释已经很全，也可以参考以下内容：
https://blog.csdn.net/subiluo/article/details/81912732

% -------------------------------------------------------------------------
%
% File : DynamicWindowApproachSample.m
%
% Discription : Mobile Robot Motion Planning with Dynamic Window Approach
%
% Environment : Matlab
%
% Author : Atsushi Sakai
%
% Copyright (c): 2014 Atsushi Sakai
%
% License : Modified BSD Software License Agreement
% log: 20181031 增加详细的注释信息 下标的定义
% 20181101 ：增加画出障碍物的大小，更直观的看到障碍物和机器人之间的位置关系
% -------------------------------------------------------------------------
 




function [] = DynamicWindowApproachSample()

close all;
clear all;

disp('Dynamic Window Approach sample program start!!')

%% 机器人的初期状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
% x=[0 0 pi/2 0 0]'; % 5x1矩阵 列矩阵  位置 0，0 航向 pi/2 ,速度、角速度均为0
x = [0 0 pi/10 0 0]'; 

% 下标宏定义 状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
POSE_X      = 1;  %坐标 X
POSE_Y      = 2;  %坐标 Y
YAW_ANGLE   = 3;  %机器人航向角
V_SPD       = 4;  %机器人速度
W_ANGLE_SPD = 5;  %机器人角速度 

goal = [10,10];   % 目标点位置 [x(m),y(m)]

% 障碍物位置列表 [x(m) y(m)]
obstacle=[0 2;
          2 4;
          2 5;      
          4 2;
%           4 4;
          5 4;
%           5 5;
          5 6;
          5 9
          8 8
          8 9
          7 9];
% obstacle=[0 2;
%           4 2;
%           4 4;
%           5 4;
%           5 5;
%           5 6;
%           5 9
%           8 8
%           8 9
%           7 9
%           6 5
%           6 3
%           6 8
%           6 7
%           7 4
%           9 8
%           9 11
%           9 6];
      
obstacleR = 0.5;% 冲突判定用的障碍物半径
global dt; 
dt = 0.1;% 时间[s]

% 机器人运动学模型参数
% 最高速度m/s],最高旋转速度[rad/s],加速度[m/ss],旋转加速度[rad/ss],
% 速度分辨率[m/s],转速分辨率[rad/s]]
Kinematic = [1.0,toRadian(20.0),0.2,toRadian(50.0),0.01,toRadian(1)];
%定义Kinematic的下标含义
MD_MAX_V    = 1;%   最高速度m/s]
MD_MAX_W    = 2;%   最高旋转速度[rad/s]
MD_ACC      = 3;%   加速度[m/ss]
MD_VW       = 4;%   旋转加速度[rad/ss]
MD_V_RESOLUTION  = 5;%  速度分辨率[m/s]
MD_W_RESOLUTION  = 6;%  转速分辨率[rad/s]]


% 评价函数参数 [heading,dist,velocity,predictDT]
% 航向得分的比重、距离得分的比重、速度得分的比重、向前模拟轨迹的时间
evalParam = [0.05, 0.2 ,0.1, 3.0];

area      = [-1 11 -1 11];% 模拟区域范围 [xmin xmax ymin ymax]

% 模拟实验的结果
result.x=[];   %累积存储走过的轨迹点的状态值 
tic; % 估算程序运行时间开始

% movcount=0;
%% Main loop   循环运行 5000次 指导达到目的地 或者 5000次运行结束
for i = 1:5000  
    % DWA参数输入 返回控制量 u = [v(m/s),w(rad/s)] 和 轨迹
    [u,traj] = DynamicWindowApproach(x,Kinematic,goal,evalParam,obstacle,obstacleR);
    x = f(x,u);% 机器人移动到下一个时刻的状态量 根据当前速度和角速度推导 下一刻的位置和角度
    
    % 历史轨迹的保存
    result.x = [result.x; x'];  %最新结果 以列的形式 添加到result.x
    
    % 是否到达目的地
    if norm(x(POSE_X:POSE_Y)-goal')<0.5   % norm函数来求得坐标上的两个点之间的距离
        disp('Arrive Goal!!');break;
    end
    
    %====Animation====
    hold off;               % 关闭图形保持功能。 新图出现时，取消原图的显示。
    ArrowLength = 0.5;      % 箭头长度
    
    % 机器人
    % quiver(x,y,u,v) 在 x 和 y 中每个对应元素对组所指定的坐标处将向量绘制为箭头
    quiver(x(POSE_X), x(POSE_Y), ArrowLength*cos(x(YAW_ANGLE)), ArrowLength*sin(x(YAW_ANGLE)), 'ok'); % 绘制机器人当前位置的航向箭头
    hold on;                                                     %启动图形保持功能，当前坐标轴和图形都将保持，从此绘制的图形都将添加在这个图形的基础上，并自动调整坐标轴的范围
    
    plot(result.x(:,POSE_X),result.x(:,POSE_Y),'-b');hold on;    % 绘制走过的所有位置 所有历史数据的 X、Y坐标
    plot(goal(1),goal(2),'*r');hold on;                          % 绘制目标位置
    
    %plot(obstacle(:,1),obstacle(:,2),'*k');hold on;              % 绘制所有障碍物位置
    DrawObstacle_plot(obstacle,obstacleR);
    
    % 探索轨迹 画出待评价的轨迹
    if ~isempty(traj) %轨迹非空
        for it=1:length(traj(:,1))/5    %计算所有轨迹数  traj 每5行数据 表示一条轨迹点
            ind = 1+(it-1)*5; %第 it 条轨迹对应在traj中的下标 
            plot(traj(ind,:),traj(ind+1,:),'-g');hold on;  %根据一条轨迹的点串画出轨迹   traj(ind,:) 表示第ind条轨迹的所有x坐标值  traj(ind+1,:)表示第ind条轨迹的所有y坐标值
        end
    end
    
    axis(area); %根据area设置当前图形的坐标范围，分别为x轴的最小、最大值，y轴的最小最大值
    grid on;
    drawnow;  %刷新屏幕. 当代码执行时间长，需要反复执行plot时，Matlab程序不会马上把图像画到figure上，这时，要想实时看到图像的每一步变化情况，需要使用这个语句。
    %movcount = movcount+1;
    %mov(movcount) = getframe(gcf);%  记录动画帧
end
toc  %输出程序运行时间  形式：时间已过 ** 秒。
%movie2avi(mov,'movie.avi');  %录制过程动画 保存为 movie.avi 文件

%% 绘制所有障碍物位置
% 输入参数：obstacle 所有障碍物的坐标   obstacleR 障碍物的半径
function [] = DrawObstacle_plot(obstacle,obstacleR)
r = obstacleR; 
theta = 0:pi/20:2*pi;
for id=1:length(obstacle(:,1))
 x = r * cos(theta) + obstacle(id,1); 
 y = r  *sin(theta) + obstacle(id,2);
 plot(x,y,'-m');hold on; 
end
% plot(obstacle(:,1),obstacle(:,2),'*m');hold on;              % 绘制所有障碍物位置
    


%% DWA算法实现 
% model  机器人运动学模型  最高速度m/s],最高旋转速度[rad/s],加速度[m/ss],旋转加速度[rad/ss], 速度分辨率[m/s],转速分辨率[rad/s]]
% 输入参数：当前状态、模型参数、目标点、评价函数的参数、障碍物位置、障碍物半径
% 返回参数：控制量 u = [v(m/s),w(rad/s)] 和 轨迹集合 N * 31  （N：可用的轨迹数）
% 选取最优参数的物理意义：在局部导航过程中，使得机器人避开障碍物，朝着目标以较快的速度行驶。
function [u,trajDB] = DynamicWindowApproach(x,model,goal,evalParam,ob,R)
% Dynamic Window [vmin,vmax,wmin,wmax] 最小速度 最大速度 最小角速度 最大角速度速度
Vr = CalcDynamicWindow(x,model);  % 根据当前状态 和 运动模型 计算当前的参数允许范围

% 评价函数的计算 evalDB N*5  每行一组可用参数 分别为 速度、角速度、航向得分、距离得分、速度得分
%               trajDB      每5行一条轨迹 每条轨迹都有状态x点串组成
[evalDB,trajDB]= Evaluation(x,Vr,goal,ob,R,model,evalParam);  %evalParam 评价函数参数 [heading,dist,velocity,predictDT]

if isempty(evalDB)
    disp('no path to goal!!');
    u=[0;0];return;
end

% 各评价函数正则化
evalDB = NormalizeEval(evalDB);

% 最终评价函数的计算
feval=[];
for id=1:length(evalDB(:,1))
    feval = [feval;evalParam(1:3)*evalDB(id,3:5)']; %根据评价函数参数 前三个参数分配的权重 计算每一组可用的路径参数信息的得分
end
evalDB = [evalDB feval]; % 最后一组
 
[maxv,ind] = max(feval);% 选取评分最高的参数 对应分数返回给 maxv  对应下标返回给 ind
u = evalDB(ind,1:2)';% 返回最优参数的速度、角速度  

%% 评价函数 内部负责产生可用轨迹
% 输入参数 ：当前状态、参数允许范围（窗口）、目标点、障碍物位置、障碍物半径、评价函数的参数
% 返回参数：
%           evalDB N*5  每行一组可用参数 分别为 速度、角速度、航向得分、距离得分、速度得分
%           trajDB      每5行一条轨迹 每条轨迹包含 前向预测时间/dt + 1 = 31 个轨迹点（见生成轨迹函数）
function [evalDB,trajDB] = Evaluation(x,Vr,goal,ob,R,model,evalParam)
evalDB = [];
trajDB = [];
for vt = Vr(1):model(5):Vr(2)       %根据速度分辨率遍历所有可用速度： 最小速度和最大速度 之间 速度分辨率 递增 
    for ot=Vr(3):model(6):Vr(4)     %根据角度分辨率遍历所有可用角速度： 最小角速度和最大角速度 之间 角度分辨率 递增  
        % 轨迹推测; 得到 xt: 机器人向前运动后的预测位姿; traj: 当前时刻 到 预测时刻之间的轨迹（由轨迹点组成）
        [xt,traj] = GenerateTrajectory(x,vt,ot,evalParam(4),model);  %evalParam(4),前向模拟时间;
        % 各评价函数的计算
        heading = CalcHeadingEval(xt,goal); % 前项预测终点的航向得分  偏差越小分数越高
        dist    = CalcDistEval(xt,ob,R);    % 前项预测终点 距离最近障碍物的间隙得分 距离越远分数越高
        vel     = abs(vt);                  % 速度得分 速度越快分越高
        stopDist = CalcBreakingDist(vel,model); % 制动距离的计算
        if dist > stopDist % 如果可能撞到最近的障碍物 则舍弃此路径 （到最近障碍物的距离 大于 刹车距离 才取用）
            evalDB = [evalDB;[vt ot heading dist vel]];
            trajDB = [trajDB;traj];   % 每5行 一条轨迹  
        end
    end
end

%% 归一化处理 
% 每一条轨迹的单项得分除以本项所有分数和
function EvalDB=NormalizeEval(EvalDB)
% 评价函数正则化
if sum(EvalDB(:,3))~= 0
    EvalDB(:,3) = EvalDB(:,3)/sum(EvalDB(:,3));  %矩阵的数除  单列矩阵的每元素分别除以本列所有数据的和
end
if sum(EvalDB(:,4))~= 0
    EvalDB(:,4) = EvalDB(:,4)/sum(EvalDB(:,4));
end
if sum(EvalDB(:,5))~= 0
    EvalDB(:,5) = EvalDB(:,5)/sum(EvalDB(:,5));
end

%% 单条轨迹生成、轨迹推演函数
% 输入参数： 当前状态、vt当前速度、ot角速度、evaldt 前向模拟时间、机器人模型参数（没用到）
% 返回参数; 
%           x   : 机器人模拟时间内向前运动 预测的终点位姿(状态); 
%           traj: 当前时刻 到 预测时刻之间 过程中的位姿记录（状态记录） 当前模拟的轨迹  
%                  轨迹点的个数为 evaldt / dt + 1 = 3.0 / 0.1 + 1 = 31
%           
function [x,traj] = GenerateTrajectory(x,vt,ot,evaldt,model)
global dt;
time = 0;
u = [vt;ot];% 输入值
traj = x;   % 机器人轨迹
while time <= evaldt   
    time = time+dt; % 时间更新
    x = f(x,u);     % 运动更新 前项模拟时间内 速度、角速度恒定
    traj = [traj x]; % 每一列代表一个轨迹点 一列一列的添加
end

%% 计算制动距离 
%根据运动学模型计算制动距离, 也可以考虑成走一段段圆弧的累积 简化可以当一段段小直线的累积
function stopDist = CalcBreakingDist(vel,model)
global dt;
MD_ACC   = 3;% 
stopDist=0;
while vel>0   %给定加速度的条件下 速度减到0所走的距离
    stopDist = stopDist + vel*dt;% 制动距离的计算 
    vel = vel - model(MD_ACC)*dt;% 
end

%% 障碍物距离评价函数  （机器人在当前轨迹上与最近的障碍物之间的距离，如果没有障碍物则设定一个常数）
% 输入参数：位姿、所有障碍物位置、障碍物半径
% 输出参数：当前预测的轨迹终点的位姿距离所有障碍物中最近的障碍物的距离 如果大于设定的最大值则等于最大值
% 距离障碍物距离越近分数越低
function dist = CalcDistEval(x,ob,R)
dist=100;
for io = 1:length(ob(:,1))  
    disttmp = norm(ob(io,:)-x(1:2)')-R; %到第io个障碍物的距离 - 障碍物半径  ！！！有可能出现负值吗？？
    if dist > disttmp   % 大于最小值 则选择最小值
        dist = disttmp;
    end
end
 
% 障碍物距离评价限定一个最大值，如果不设定，一旦一条轨迹没有障碍物，将太占比重
if dist >= 2*R %最大分数限制
    dist = 2*R;
end
 
%% heading的评价函数计算
% 输入参数：当前位置、目标位置
% 输出参数：航向参数得分  当前车的航向和相对于目标点的航向 偏离程度越小 分数越高 最大180分
function heading = CalcHeadingEval(x,goal)
theta = toDegree(x(3));% 机器人朝向
goalTheta = toDegree(atan2(goal(2)-x(2),goal(1)-x(1)));% 目标点相对于机器人本身的方位 
if goalTheta > theta
    targetTheta = goalTheta-theta;% [deg]
else
    targetTheta = theta-goalTheta;% [deg]
end
 
heading = 180 - targetTheta;  

%% 计算动态窗口
% 返回 最小速度 最大速度 最小角速度 最大角速度速度
function Vr = CalcDynamicWindow(x,model)

V_SPD       = 4;%机器人速度
W_ANGLE_SPD = 5;%机器人角速度 

MD_MAX_V = 1;% 
MD_MAX_W = 2;% 
MD_ACC   = 3;% 
MD_VW    = 4;% 

global dt;
% 车子速度的最大最小范围 依次为：最小速度 最大速度 最小角速度 最大角速度速度
Vs=[0 model(MD_MAX_V) -model(MD_MAX_W) model(MD_MAX_W)];
 
% 根据当前速度以及加速度限制计算的动态窗口  依次为：最小速度 最大速度 最小角速度 最大角速度速度
Vd = [x(V_SPD)-model(MD_ACC)*dt x(V_SPD)+model(MD_ACC)*dt x(W_ANGLE_SPD)-model(MD_VW)*dt x(W_ANGLE_SPD)+model(MD_VW)*dt];
 
% 最终的Dynamic Window
Vtmp = [Vs;Vd];  %2 X 4  每一列依次为：最小速度 最大速度 最小角速度 最大角速度速度
Vr = [max(Vtmp(:,1)) min(Vtmp(:,2)) max(Vtmp(:,3)) min(Vtmp(:,4))];
 
%% Motion Model 根据当前状态推算下一个控制周期（dt）的状态
% u = [vt; wt];当前时刻的速度、角速度 x = 状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
function x = f(x, u)
global dt;
F = [1 0 0 0 0
     0 1 0 0 0
     0 0 1 0 0
     0 0 0 0 0
     0 0 0 0 0];
 
B = [dt*cos(x(3)) 0
    dt*sin(x(3)) 0
    0 dt
    1 0
    0 1];
 
x= F*x+B*u;  

%% degree to radian
function radian = toRadian(degree)
radian = degree/180*pi;

%% radian to degree
function degree = toDegree(radian)
degree = radian/pi*180;

%% END