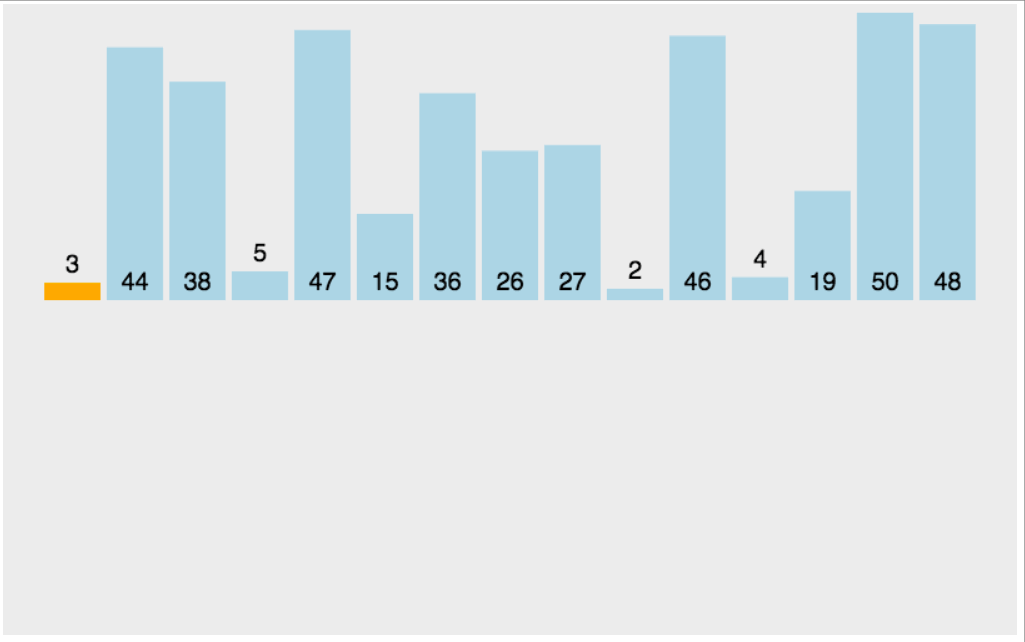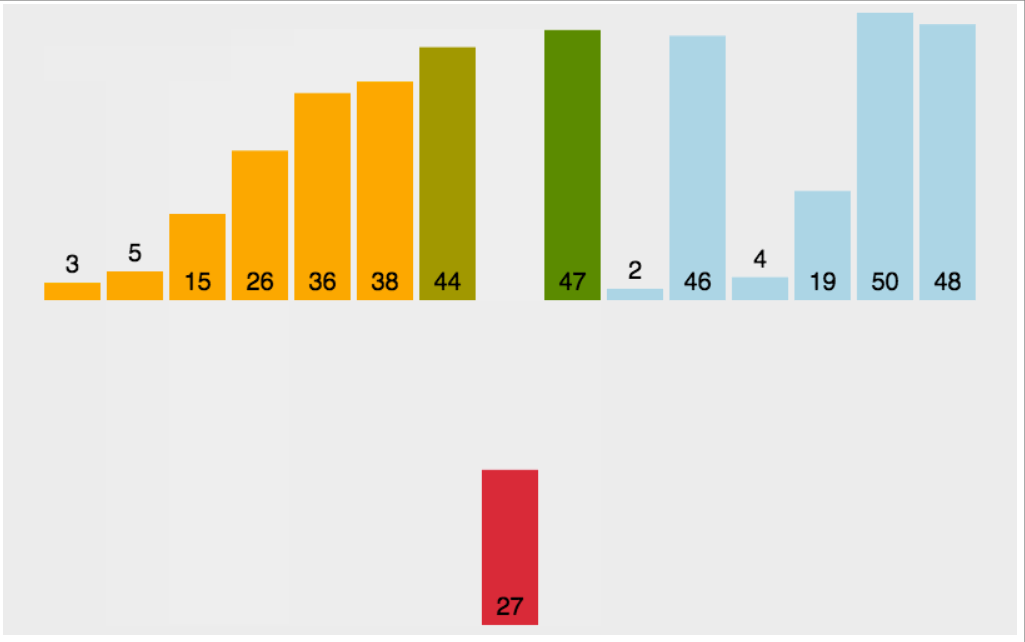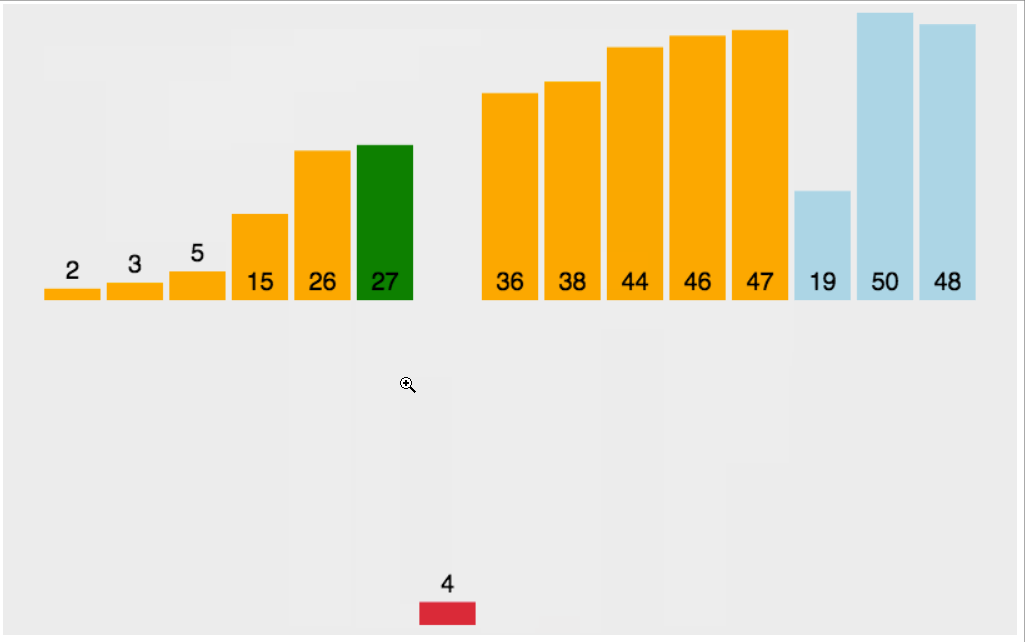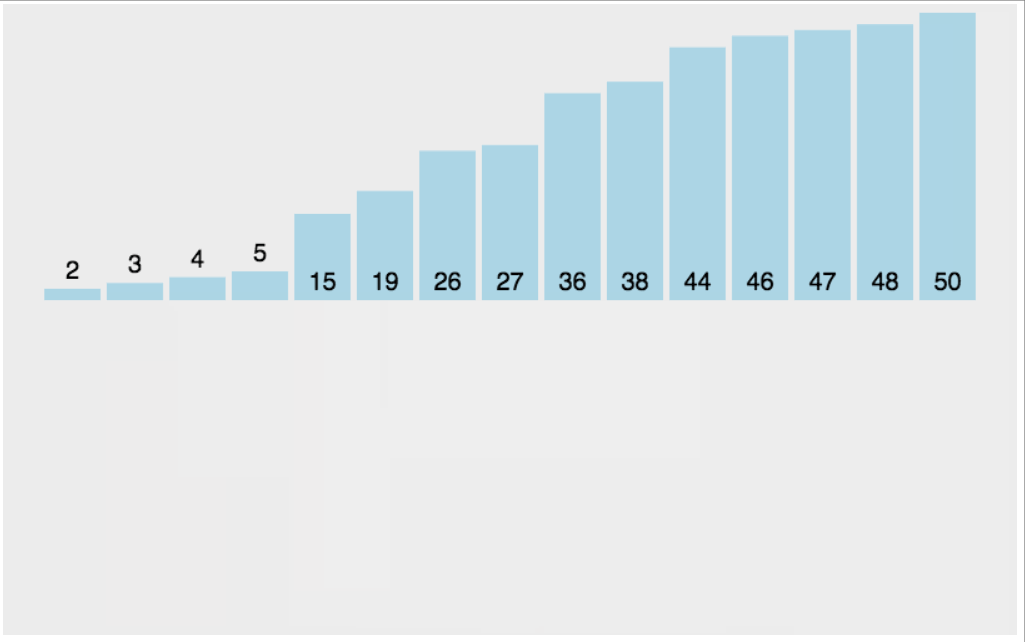
插入排序是一种简单且稳定的排序算法，适合小规模数据或部分有序数据。

// 插入排序函数
void insertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) { // 从第二个元素开始
        int key = arr[i]; // 当前需要插入的元素
        int j = i - 1;

        // 将比 key 大的元素向后移动
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key; // 插入 key 到正确位置
    }
}

#include <stdio.h>
// 打印数组函数
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    int arr[] = {12, 11, 13, 5, 6}; // 待排序数组
    int n = sizeof(arr) / sizeof(arr[0]); // 计算数组长度

    printf("排序前的数组: \n");
    printArray(arr, n);

    insertionSort(arr, n); // 调用插入排序函数

    printf("排序后的数组: \n");
    printArray(arr, n);

    return 0;
}

优化建议

1.二分查找优化：在已排序部分使用二分查找确定插入位置，减少比较次数。

void insertionSortOptimized(int arr[], int n) {
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int left = 0, right = i - 1;

        // 二分查找插入位置
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (arr[mid] > key) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        // 移动元素
        for (int j = i - 1; j >= left; j--) {
            arr[j + 1] = arr[j];
        }
        arr[left] = key; // 插入 key
    }
}

2.小规模数据：插入排序在小规模数据或部分有序数据中表现优异。

3.结合其他排序算法：在快速排序或归并排序中，对小规模子数组使用插入排序。