空间划分技术在CAD建模中被广泛应用，用于提高建模计算的效率。经过不断研究，衍生出了各种各样的空间划分技术，从对空间简单等分的空间格，到有固定划分结构的八叉树、KD树，再到根据实际场景自适应划分的BVH（Boundary Volume Hierarchy）、R-Tree，总能找到一种适合应用场景的类型。

​       作为一种辅助性的空间数据结构，空间划分技术介于操作算法和几何对象之间，它通过筛选作用，排除大量与特定空间操作无关的几何对象，从而大大提高空间操作的效率。本文以八叉树为例，讲解空间划分的基本原理和应用。

1.基本原理

       八叉树相关的操作有2个：构造和查询。

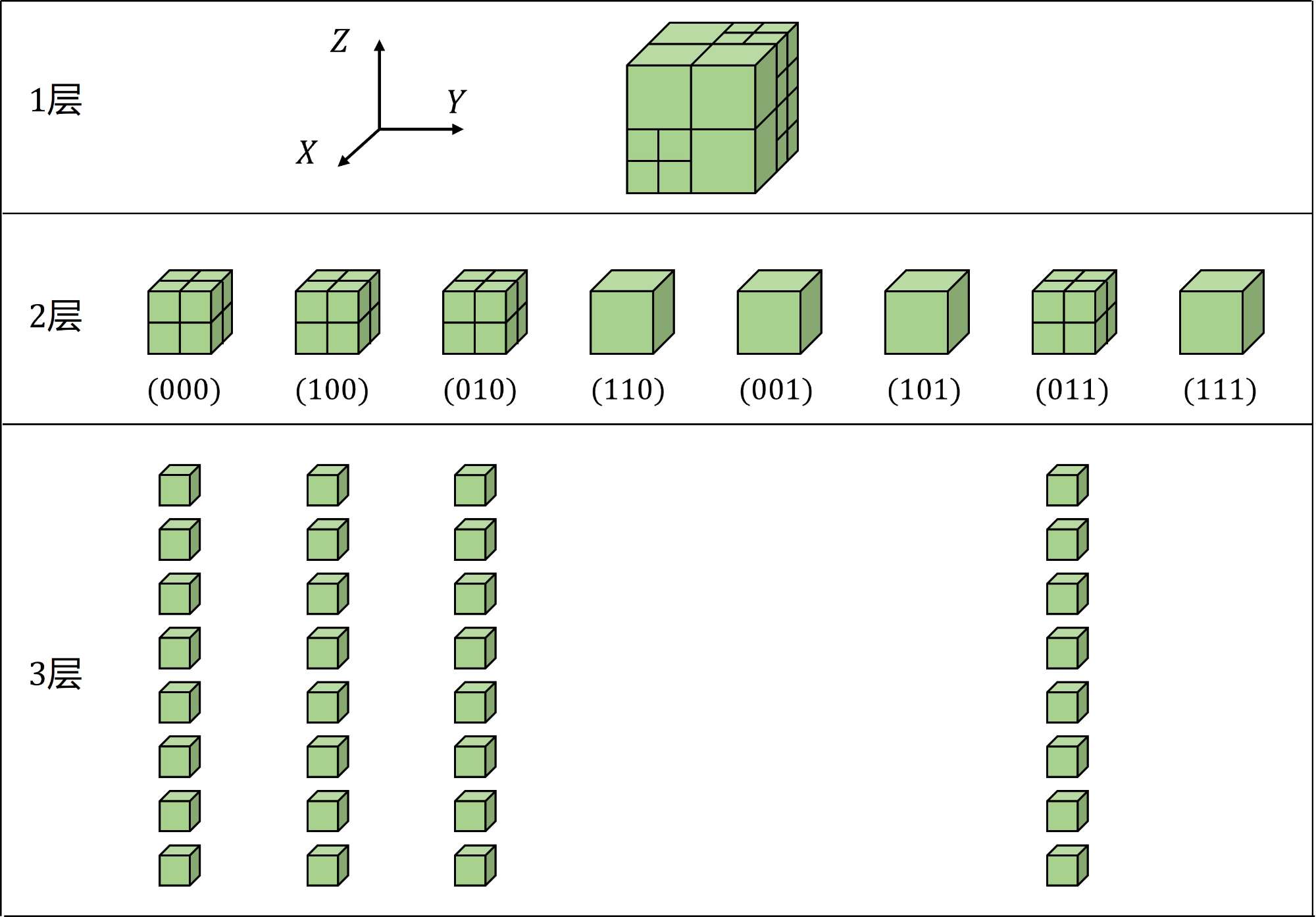
       构造。如图1所示，蓝色为由一系列三角形组成的弯管状网格，绿色为网格创建的八叉树。如图2所示，上述八叉树有三层结构，第一层仅有1个根节点，第二层是根节点分裂而来的8个子节点，第三层的子节点更多，是由第二层的节点分裂而来的。需要注意的是，不是每个第二层的节点都会再次分裂。为了方便讲述，我们将第二层的子节点按坐标轴进行编号，即$(X,Y,Z)$，数字0代表在坐标轴的离原点近的地方，数字1反之，比如$(1,0,0)$在前面左下角的位置。第二层的4个节点，被分裂成了更小的8个子节点，分别是$(0,0,0)$、$(1,0,0)$、$(0,1,0)$、$(0,1,1)$，而其它节点没有再被细分，这是因为在这几个节点对应的空间中没有几何对象，如果被细分了，反而会增加存储空间和查询时间。在八叉树中，虽然有些节点不会被细分，但一旦被细分，一定会是分裂为8个子节点。
 

       简单讲解一下上述八叉树可能的构造过程：（1）确定包围几何对象的包容盒，包括每个三角形的包围盒和整个网格的包围盒；（2）创建八叉树的根节点，其对应的空间就是整个网格的包围盒，这也是后续操作的最大空间；（3）依次将三角形放入八叉树中。对于某一三角形，从根节点开始，依次用其包围盒与子节点判断是否相交，如果相交，则为相关节点，继续与相关节点的子节点判断是否相交，如此不断深度遍历，直到树的最大层数的节点，将此三角形存储在这个叶子节点中。在此过程中，相关节点（即存在三角形的包容盒与之相交）被分裂，即子节点被创建出来。

       查询。查询的过程与构造相似，假设我们要考虑的问题是平面与图1中的网格求交。首先，利用平面与八叉树中的节点包围盒判断相交，深度遍历获取所有的相关叶子节点，然后，将叶子节点中的三角形取出，查询结束。后面就是对平面和被筛选出的三角形进行真正的求交操作了。

       使用八叉树之前，需要考虑这几件事情：

• 构建八叉树的终止条件是什么？固定层数？最大层数？叶子节点中的几何对象数？这会影响构建效率和查询效率。
• 何时创建八叉树的节点？是在开始时一并创建，还是构建过程中按需创建？这涉及到内存分配方式，可能极大的影响构建时间。
• 几何对象存储方式，是只存储在叶子节点上，还是也存在中间节点上？这会影响查询时的筛选效果。
   

2. 应用实例

       考虑这样一个经典问题：如图3所示，沿某一确定方向，计算一系列点在网格上的投影点。最简单直接的方法是：对于每个点，沿设定方向作直线，然后与每个三角形求交。简单直接法实现起来非常简单，但是，当点非常多时，效率非常差，因为直接法的时间复杂度是$O(n\ast m)$，其中，$n$是待投影点的个数，$m$是网格包含三角形的个数。
 

       由于该问题是固定方向的，可以进行降维，将大部分计算限定在XY平面进行。如果固定方向不是Z轴，则以固定方向为Z轴构建局部坐标系，并进行坐标转换即可。这样，简单直接法中判断直线与三角形是否相交，就可以转换为判断点是否在三角形内，这可以大大减少计算量。

       基于上面的降维处理，如果点数较多，简单直接法还可以被优化：首先，计算每个三角形的的XY包容盒，并存储起来；然后，直线与三角形求交之前，先判断点是否在相应的XY包容盒内，如果不在里面，则直线肯定不与三角形相交，从而筛选掉大量不相关的三角形，但优化直接法的时间复杂度依然是$O(n\ast m)$。

       对于空间划分方法，则可以采用四叉树，而不是八叉树，即只在XY平面上划分空间。应用四叉树的一般流程是：(1) 构造四叉树；(2) 利用树结构查询相关几何对象（这里是筛选出可能相交的三角形）；(3) 真正的计算操作（这里是计算直线与三角形的交点）。

       现在对比3种方法的实际效果，给定待投影点的个数为1,000，网格包含的三角形个数约为100,000，四叉树的层数选择为5。3种方法的投影用时见表1。四叉树方法比优化直接法快了10多倍，更是比简单直接法快了80多倍！
 

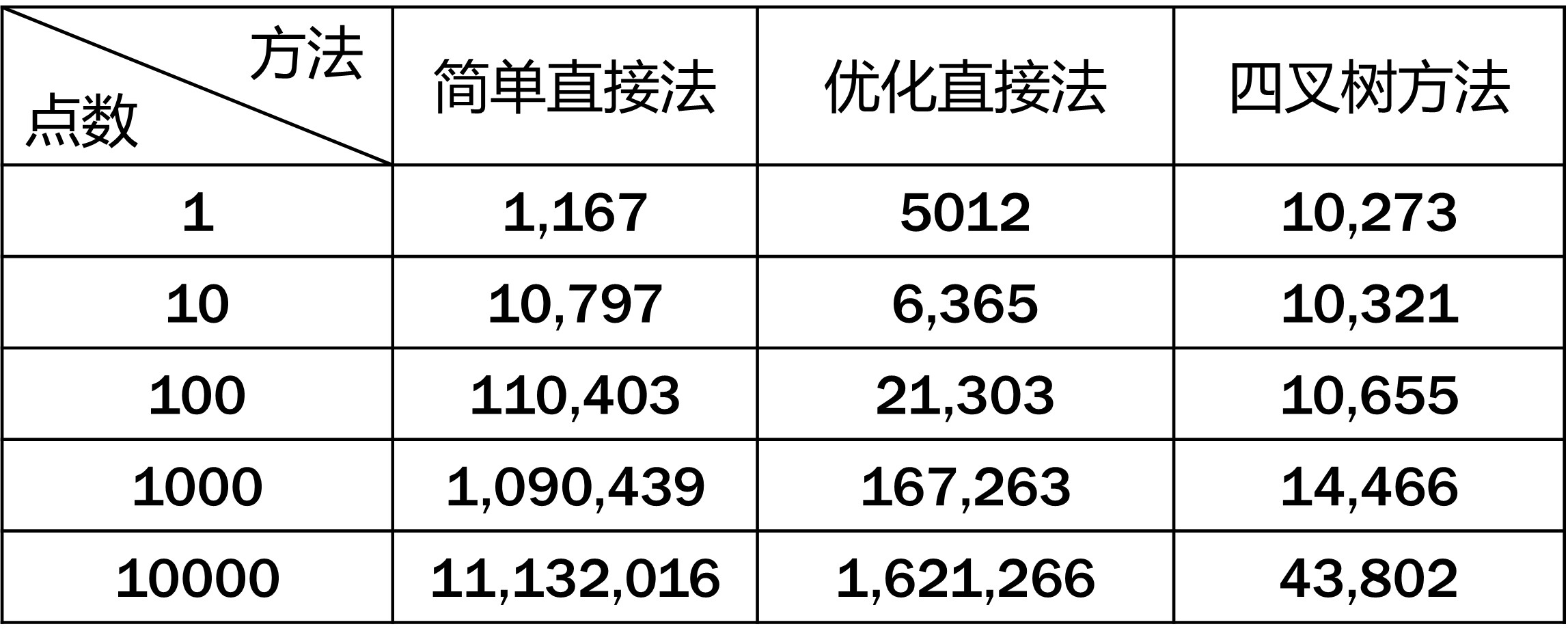
       那么，采用四叉树方法一定比直接法快吗？答案是否定的，因为四叉树方法存在构建四叉树的固定开销。这与问题规模有关，而点投影问题的规模是待投影点的个数和网格包含的三角形数目，一般两者越大，加速比越好。上述两个参数有一定相似性，本文只探讨待投影点的个数对性能表现的影响。表2是在不同点数情况下3种方法的统计结果。从表中可以看出，简单直接法的用时基本与点数呈线性相关，而另外2种方法则没有这样的关系，这是因为，在三角形个数一定的情况下，两者均存在固定开销。优化直接法的固定开销大概是4,600 us，四叉树方法的大概是10,200 us。因此，优化直接法在点数为1时效率比简单直接法差，而四叉树方法在点数为10时就不行了。相反，当点数增加到10,000时，直接法与四叉树方法的差距进一步增大。
 

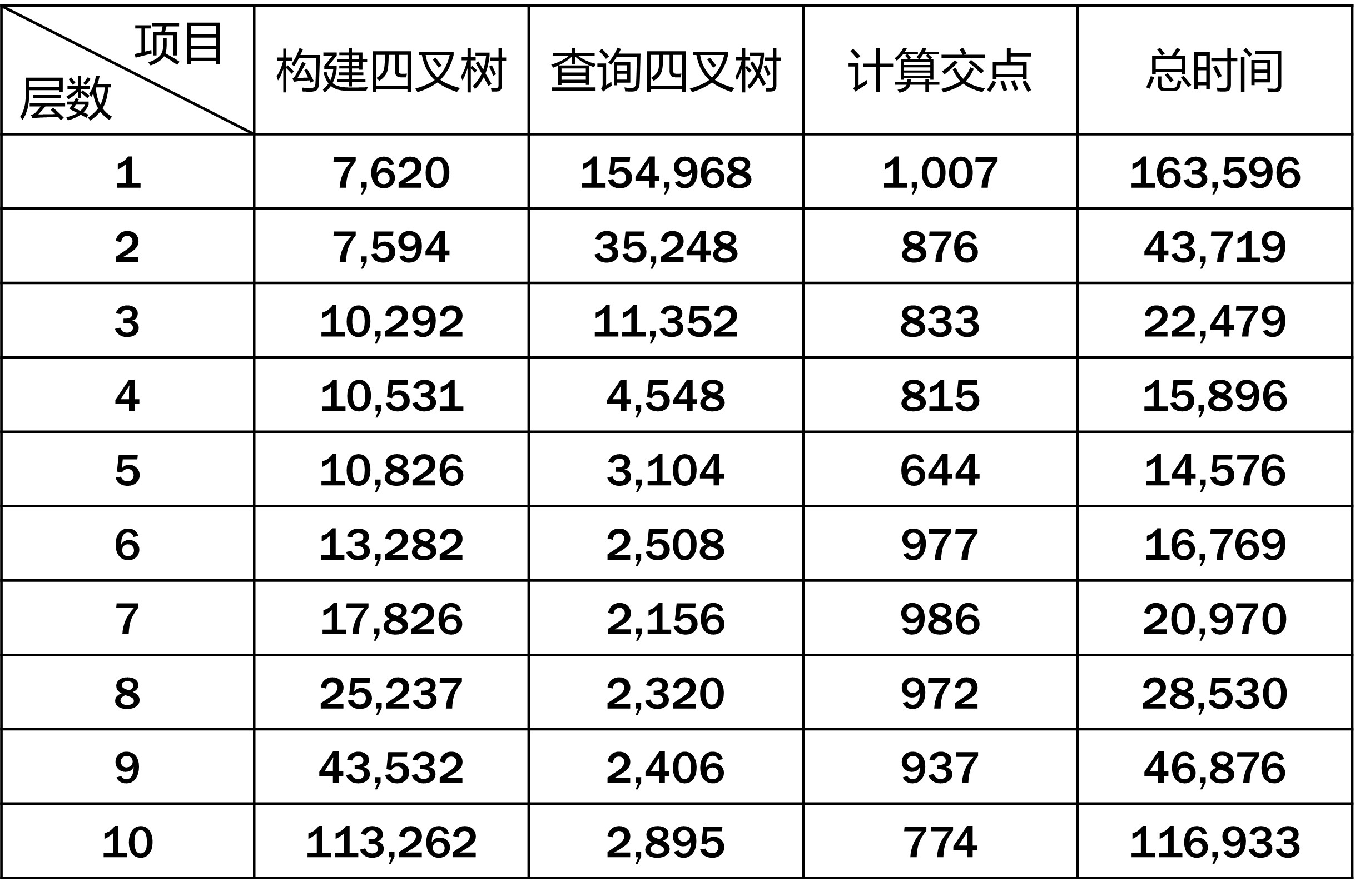
       现在探讨对四叉树应用效果影响比较大的参数：层数。直观感受是：四叉树层数太少，四叉树的筛选作用较小；层数太多，构建四叉树的时间和占用的空间可能很大，极端情况下，层数加1，节点个数翻4倍。表3是在不同层数下四叉树方法的表现。当层数为1时，效率基本与优化直接法相当，随着层数增加，效率逐渐提升，但当层数太多时，则得不偿失了。对于现在讨论的问题，最优的层数应该是4-6层。但是，影响最优层数的因素很多，比如：网格包含的三角形个数及其在空间中的分布、计算交点的复杂程度等。在这里，提供一个指标用于估计层数$k$，也就是叶子节点的平均几何对象数$t$，即：
$$t=\frac{m}{4^{k-1}}.$$
其中，$m$是网格包含三角形的个数。请注意，最优层数需要根据实际应用确定，一般会认为在 $t=10$ 附近比较合适。
 

       之所以要介绍空间划分技术，因为它们是CAD建模中必须要用的技术。后面对不同方法的分析，则希望引导读者进一步思考，并在实际应用中感受不同方法、不同参数的不同效果，毕竟“纸上得来终觉浅，绝知此事要躬行”。

文章首发于微信公众号：CAD智造干将，欢迎关注