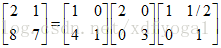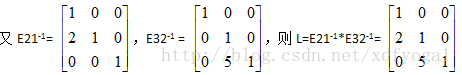前面我们曾经通过高斯消元将矩阵A最终转化成了上三角阵U,那么今天我们就继续深入探索A和U之间到底有什么样的联系。在开始之前,先交代一些需用到的基础理论。假设A是可逆阵,则有AA-1=I,两边同时转置,根据乘积的转置等于各自转置的反顺序相乘,则有(A-1)TAT=I,这个式子表示A转置的逆等于A的逆的转置,也就是说,对单个矩阵而言,转置和求逆可以任意颠倒次序。
假设矩阵A= 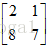
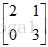
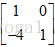
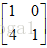
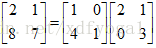
顺便提一下,有时候我们会将主元单独列出来,所以有时候我们有时候也可将A分解成
,这个称之为LDU(D表示diagonal对角阵)分解,这样看起来更平衡,因为两边是三角阵,中间是对角阵。
那么为什么我们要对A进行LU分解呢?
假设有一个3*3的矩阵A,经过E21,E31,E32消元后得到U。
举一个具体的例子,假设E21= 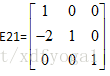

从上面的L中可看出,如果不存在行互换,消元乘数(1、2行之间的消元乘数2和2、3行之间的消元乘数5)可直接写入L中,因此我们又可以用一种新的角度来看待消元,当我们进行消元步骤时,只要步骤正确,那么我们可以在得到LU的过程中把A扔掉,当完成A第二行中的消元,U中则保存了新的第二行,同时L中得到了消元所用的乘数,然后我们可以不用再考虑A了,因为A中所有的信息都包含于U和L中。这是对消元的另一种全新认识。
现在考虑一个问题,对于一个n*n的矩阵A,假如一次乘法和加法算一次操作,那么需要多少次操作才能完成所有的消元?
首先第一行下面的所有元素都要进行乘法和加法的操作,所以第一批消元应该是n*(n-1)次操作,为了后面计算方便,假设需要n2次操作,然后第二行下面的元素需要(n-1)2次操作,后面以此类推,得到共需要消元次数n2+(n-1)2+…+12,利用积分,可得操作次数大概是n的三次方级别,这是求变换A需要多少次操作,那么对于右侧常数列b,易得其需要n2级别操作,而我们经常会遇到矩阵A和好几个右侧向量b的情形,所以如果我们之前花时间将A先分解为LU,那么之后就可以以较少操作次数去处理每一个右侧向量b了。