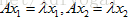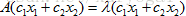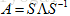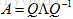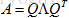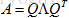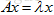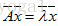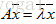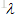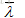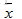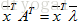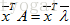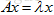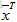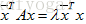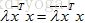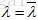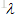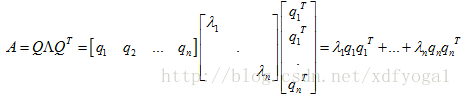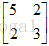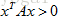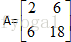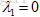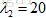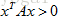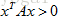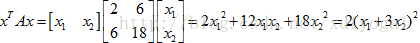对称阵是非常重要的矩阵,对于实对称矩阵,其特征值也为实数,且特征向量是垂直的。注意这里的垂直是指:如果特征值互不相同,那么每个特征值对应的特征向量是在一条线上,那些线之间总是垂直的;如果特征值重复,那特征值就对应一整个平面的特征向量,这是因为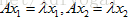 ,则
,则 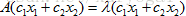 ,在那个平面上,我们总可以选到垂直的向量。比如对于单位阵,它是对称阵,单位阵只有一个特征值即为1,每个向量都是其特征向量,在这些特征向量组成的平面上,总能够挑选出一组垂直的。由于对称阵的n个无关特征向量总是垂直的,因此矩阵原来的对角化形式
,在那个平面上,我们总可以选到垂直的向量。比如对于单位阵,它是对称阵,单位阵只有一个特征值即为1,每个向量都是其特征向量,在这些特征向量组成的平面上,总能够挑选出一组垂直的。由于对称阵的n个无关特征向量总是垂直的,因此矩阵原来的对角化形式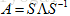 可变成
可变成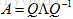 ,其中Q为正交阵,正交阵的逆等于其转置,因此对称矩阵可进一步分解为
,其中Q为正交阵,正交阵的逆等于其转置,因此对称矩阵可进一步分解为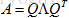 ,这是线性代数中的一个有名的定理:给定一个对称矩阵A,一定能分解成
,这是线性代数中的一个有名的定理:给定一个对称矩阵A,一定能分解成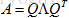 这样的形式,即正交矩阵乘以对角矩阵乘以正交矩阵的转置,这在数学上称为谱定理,谱(spectrum)就是指矩阵的特征值集合,在力学上,这常称为主轴定理。
这样的形式,即正交矩阵乘以对角矩阵乘以正交矩阵的转置,这在数学上称为谱定理,谱(spectrum)就是指矩阵的特征值集合,在力学上,这常称为主轴定理。
为什么实对称阵的特征值是实数?
从定义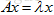 开始推导,两边取共轭则有
开始推导,两边取共轭则有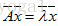 , 因为讨论的是实对称阵,因此可以写成
, 因为讨论的是实对称阵,因此可以写成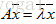 ,这个式子说明如果矩阵A有特征值
,这个式子说明如果矩阵A有特征值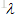 和特征向量x,那它一定有另一特征值
和特征向量x,那它一定有另一特征值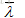 和特征向量
和特征向量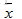 ,对方程转置,则
,对方程转置,则 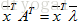 ,则
,则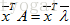 ,同乘x,则
,同乘x,则 ;对
;对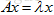 两边同乘
两边同乘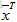 ,则有
,则有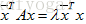 ,两式左侧相同,因此有
,两式左侧相同,因此有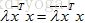 ,因为我们不关心特征向量是零向量的情况,因此有
,因为我们不关心特征向量是零向量的情况,因此有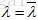 ,则
,则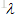 是实数。
是实数。
现在我们换一种思维去理解谱定理,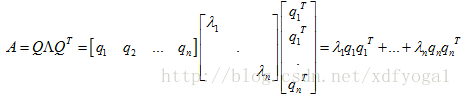 ,标准正交特征向量,实特征值,上式表示每个对称阵都可表示为其相互垂直的特征向量的组合。
,标准正交特征向量,实特征值,上式表示每个对称阵都可表示为其相互垂直的特征向量的组合。
前面所讲的行列式方法求特征值基本是针对小规模矩阵的,比如2*2,3*3的矩阵,对于大规模矩阵这种求法是无能为力的,比如50*50的矩阵。对于这种大规模矩阵,我们只能对其特征值作些定性的分析,比如对于50阶矩阵,其主元是较容易求得的,由于主元的乘积等于行列式,而特征值的乘积又等于行列式,因此主元的乘积就等于特征值的乘积,另外对于对称阵,我们还有主元的符号与特征值的符号一致,个数相同,正主元个数等于正特征值个数。
正定矩阵(positive definite matrix)
首先正定矩阵都是对称的,且所有特征值都是正数,举个例子,假设对称阵A= 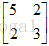 ,经过消元可知其两个主元为5和11/5,都为正,因此A为正定阵,主元的乘积等于行列式,则A的行列式为5*11/5=11,对称阵特征值的个数、正负情况与主元相同,经过计算A的特征值为
,经过消元可知其两个主元为5和11/5,都为正,因此A为正定阵,主元的乘积等于行列式,则A的行列式为5*11/5=11,对称阵特征值的个数、正负情况与主元相同,经过计算A的特征值为 ,矩阵的特征值正负在微分方程中是很重要的,因为根据特征值正负,可以确定系统稳定与否,另外对于正定矩阵还有结论:其行列式及所有子行列式都是正的。
,矩阵的特征值正负在微分方程中是很重要的,因为根据特征值正负,可以确定系统稳定与否,另外对于正定矩阵还有结论:其行列式及所有子行列式都是正的。
判定矩阵是否为正定矩阵(positive definite matrix)有以下4种方法,每种方法都是正定性的完整判断条件:
1、特征值判定:如果矩阵的所有特征值均为正,则该矩阵正定
2、行列式判定:如果矩阵的所有顺序主子式为正,则矩阵正定
3、主元判定:如果所有主元为正,则矩阵正定
4、如果对任意的非零向量x有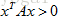 ,则矩阵A正定
,则矩阵A正定
举个例子,比如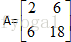 ,我们知道它是一个半正定矩阵(positive semi-definite matrix),根据特征值之和等于迹(trace,为矩阵对角线元素之和),特征值之积等于行列式(所有主元之积),又该矩阵为奇异阵,因此A的行列式为0,则一定有一特征值
,我们知道它是一个半正定矩阵(positive semi-definite matrix),根据特征值之和等于迹(trace,为矩阵对角线元素之和),特征值之积等于行列式(所有主元之积),又该矩阵为奇异阵,因此A的行列式为0,则一定有一特征值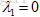 ,又迹为20,因此另一特征值
,又迹为20,因此另一特征值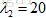 ,由此看到该矩阵的特征值大于等于0,定义为半正定也就是因为存在这个等于0,因此根据特征值判定此矩阵不是正定矩阵;再看行列式,A的第1个子行列式就是其第一个元素2,第2个子行列式就是其自身的行列式为0,则根据行列式也可判断出A不是正定阵;再根据主元判断,A只存在唯一的主元为2,不存在第2个主元,因此不满足所有主元为正,因此非正定;最后根据
,由此看到该矩阵的特征值大于等于0,定义为半正定也就是因为存在这个等于0,因此根据特征值判定此矩阵不是正定矩阵;再看行列式,A的第1个子行列式就是其第一个元素2,第2个子行列式就是其自身的行列式为0,则根据行列式也可判断出A不是正定阵;再根据主元判断,A只存在唯一的主元为2,不存在第2个主元,因此不满足所有主元为正,因此非正定;最后根据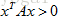 ,
,
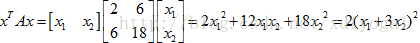
由上式可知,当x1+3x2=0时,上式等于0,不满足对任意的非零向量x都有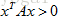 , 因此矩阵不正定。
, 因此矩阵不正定。