十四、【机器学习】【监督学习】-弹性网回归 (Elastic Net Regression)

系列文章目录

前言

在先前的文章系列中，我们深入探讨了机器学习的基础框架和算法分类，为读者构建了关于这一领域的坚实理论基础。本章节我们将焦点转向监督学习领域中的一个核心算法—— 弹性网回归 (Elastic Net Regression)，旨在详尽解析其内在逻辑、应用实践及重要参数调整策略。

一、基本定义

（一）、监督学习

监督学习（Supervised Learning）是机器学习中的一种主要方法，其核心思想是通过已知的输入-输出对（即带有标签的数据集）来训练模型，从而使模型能够泛化到未见的新数据上，做出正确的预测或分类。在监督学习过程中，算法“学习”的依据是这些已标记的例子，目标是找到输入特征与预期输出之间的映射关系。

（二）、监督学习的基本流程

数据收集：获取包含输入特征和对应正确输出标签的训练数据集。
        数据预处理：清洗数据，处理缺失值，特征选择与转换，标准化或归一化数据等，以便于模型学习。
        模型选择：选择合适的算法，如决策树、支持向量机、神经网络等。
        训练：使用训练数据集调整模型参数，最小化预测输出与实际标签之间的差距（损失函数）。
        验证与调优：使用验证集评估模型性能，调整超参数以优化模型。
        测试：最后使用独立的测试集评估模型的泛化能力，确保模型不仅在训练数据上表现良好，也能在未见过的新数据上做出准确预测。

（三）、监督学习分类算法（Classification）

定义：分类任务的目标是学习一个模型，该模型能够将输入数据分配到预定义的几个类别中的一个。这是一个监督学习问题，需要有一组已经标记好类别的训练数据，模型会根据这些数据学习如何区分不同类别。
例子：垃圾邮件检测（垃圾邮件 vs. 非垃圾邮件）、图像识别（猫 vs. 狗）。

二、弹性网回归 (Elastic Net Regression)

（一）、定义

弹性网回归（Elastic Net Regression）是一种线性回归模型，它结合了岭回归（Ridge Regression）和Lasso回归（Least Absolute Shrinkage and Selection Operator Regression）的优点，通过同时使用L1和L2正则化来解决高维数据和多重共线性问题。弹性网回归不仅能够处理多重共线性，还可以进行特征选择，避免过拟合，尤其是在特征数量远远超过样本数量的情况下。

（二）、基本概念

弹性网回归通过在损失函数中加入L1和L2两种类型的正则化项，来限制回归系数的大小和数量。L1正则化有助于特征选择，因为它可以将一些不重要的特征系数压缩至零，从而简化模型。L2正则化有助于减少模型方差，提高模型稳定性，尤其是在存在多重共线性时。弹性网回归通过一个超参数α来平衡这两种正则化方式的影响，其中α介于0和1之间，α=0时模型退化为纯粹的岭回归，α=1时模型退化为纯粹的Lasso回归。

（三）、训练过程

弹性网回归的训练过程涉及以下关键步骤：

1. 损失函数定义

弹性网回归的目标是找到一组权重𝑤w，使得预测输出尽可能接近实际输出，同时最小化模型的复杂度。其损失函数定义为：

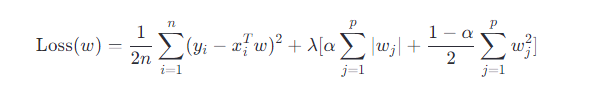
其中，

𝑦𝑖是第𝑖个样本的实际输出。
𝑥𝑖是第𝑖个样本的输入特征向量。
𝑛是样本的数量。
𝑝是特征的数量。
𝜆是正则化强度，控制正则化项的影响力。
𝛼是平衡L1和L2正则化作用的参数，范围在[0, 1]内。

2. 模型优化

优化过程通常采用迭代算法，如梯度下降或坐标下降法。在每一步迭代中，算法会更新权重向量𝑤，以降低损失函数的值。对于坐标下降法，每次迭代只更新一个权重𝑤𝑗，直到所有权重都更新完毕，然后重复此过程直至收敛。

3. 超参数选择

正则化强度𝜆λ和平衡参数𝛼α的选择对模型的性能至关重要。这些超参数可以通过交叉验证（Cross-validation）来确定，即在训练集上分割出一部分作为验证集，尝试不同的超参数组合，选择那些在验证集上表现最好的参数。

4. 模型评估

在训练完成后，应使用独立的测试集来评估模型的泛化能力，确保模型不仅能很好地拟合训练数据，还能在新数据上给出准确的预测。

（四）、特点：

双重正则化：弹性网回归结合了L1和L2正则化，能够同时实现特征选择和模型稳定性的提升。
处理多重共线性：在存在多重共线性的情况下，Lasso回归可能只选择一组相关特征中的一个，而弹性网回归则可以更公平地选择相关特征，同时保持模型的稳定性。
高维数据处理：在特征数量远大于样本数量的情况下，弹性网回归依然能够有效地进行特征选择和模型训练。

（五）、适用场景：

高维数据：特征数量远大于样本数量，需要进行特征选择和模型复杂度控制。
多重共线性：特征间存在较高的相关性，需要一个稳健的模型来避免过度依赖单一特征。
需要特征选择：在需要识别哪些特征对预测最重要时，弹性网回归可以提供有用的信息。

（六）、扩展

弹性网回归可以与其他机器学习技术结合，如集成学习、深度学习等，来进一步提高预测性能。此外，还可以通过自适应弹性网回归等方法来进一步优化特征选择过程，或者在特定应用领域中针对数据特性进行定制化改进。例如，可以将弹性网回归应用于基因表达数据分析、金融风险评估等领域，以处理高维和高度相关的特征集。

三、总结

弹性网回归是一种强大的线性模型，它结合了Lasso回归和岭回归的优点，通过同时使用L1和L2正则化，既能够处理多重共线性问题，也能够进行有效的特征选择。在高维数据集中，尤其是当特征数量远大于样本数量时，弹性网回归提供了一个实用的解决方案，可以帮助识别哪些特征对模型的预测能力贡献最大，同时保持模型的简单性和鲁棒性。通过适当的超参数调优，弹性网回归能够构建出具有良好泛化能力的模型，适用于多种数据分析和预测任务。在实际应用中，弹性网回归常常被用于生物信息学、金融分析、市场预测等领域，尤其是在处理大量潜在影响因素时，能够帮助研究人员聚焦于关键驱动因素。

更多内容，防止走丢，请关注公众号，公众号会持续更新各类技术内容和职场介绍：

码上云游