一、棋盘覆盖问题

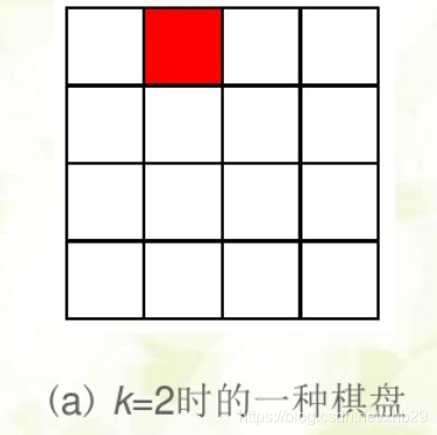
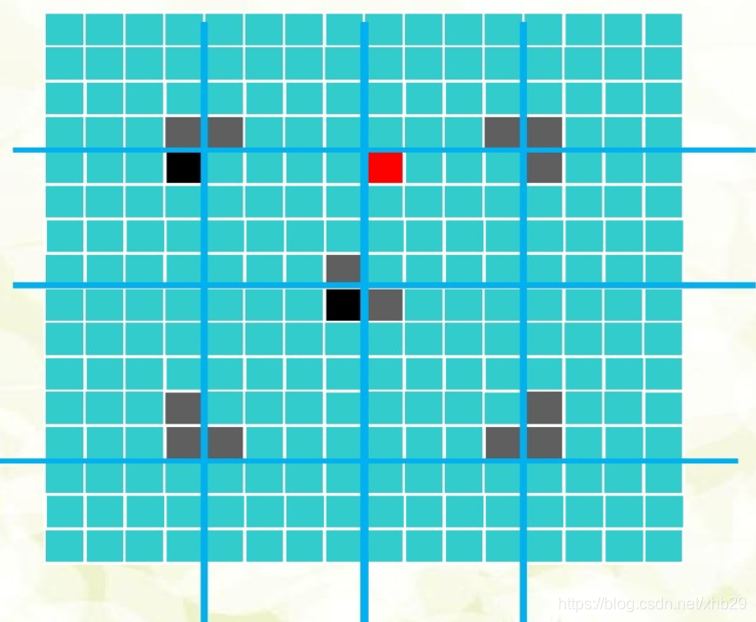
在一个2^k*2K个方格组成的棋盘，恰好有一个方格和其他方格不同，称该方格为特殊方格，且称该棋盘为特殊棋盘。显然特殊方格出现的位置有4^k情况

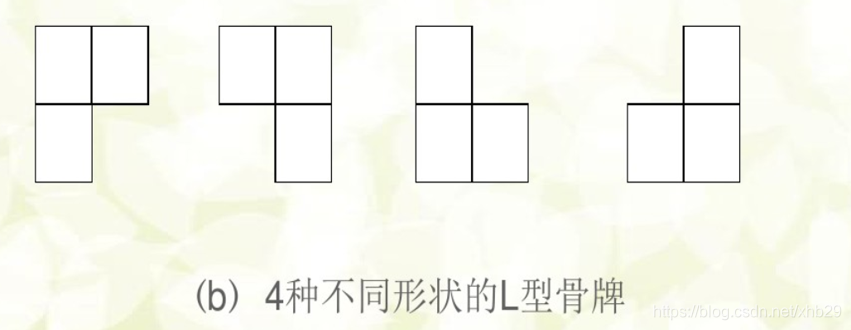
棋盘覆盖问题要求用如图（b）所示的L型骨牌给定棋盘上特殊方格以外的所有方格，且任何2个L型骨牌不得重叠

二、详细求解过程

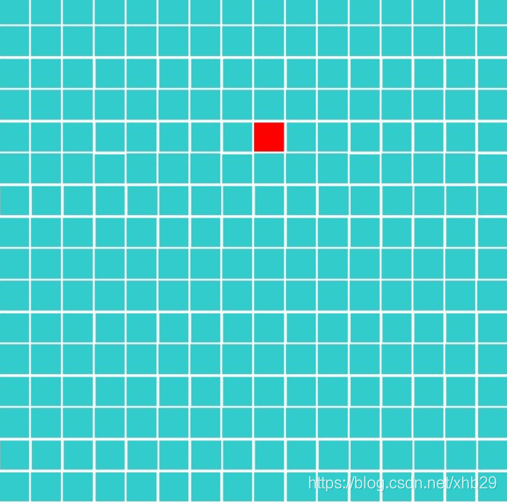
棋盘有一个特殊方格

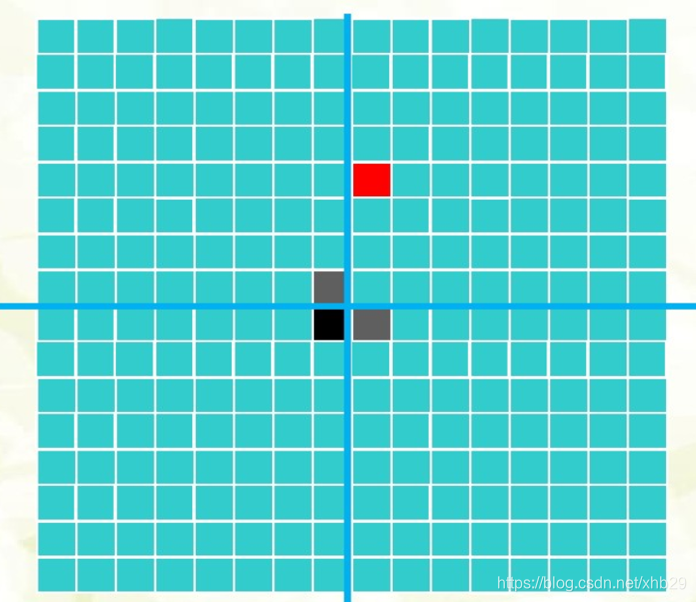
第一次分割

第二次分割

第三次分割

第四次分割

三、代码实现

主要用MFC实现的，这里就截图手写部分代码，其他部分框架都是自动生成的。用的是单文档的。
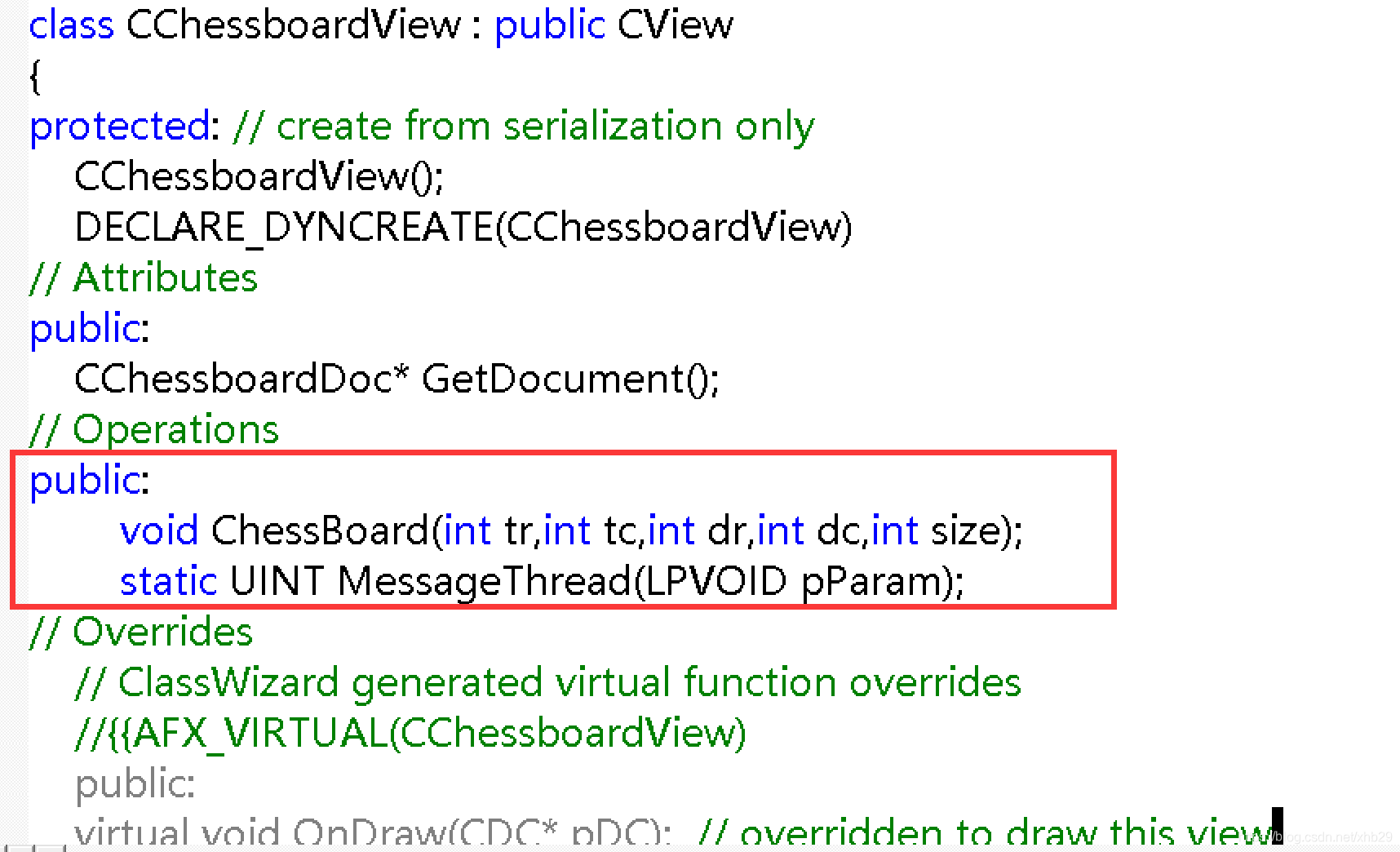
头文件代码
第一个是程序代码。
第二个是开启一个线程不开启的程序中途单击或者移动会卡死。

ondraw函数代码画出棋盘的界面

这里就是棋盘代码的整个实现程序和左键单击代码

/*
整个棋盘算法实现的程序
*/
void CChessboardView::ChessBoard(int tr,int tc,int dr,int dc,int size)
{
   
	Sleep(200);//让程序暂停下
	RECT rt;
	int s;
	if(size==1)
	{
   
	
		return;
	}
	int t =tile++;
	CString count;
	s=size/2;

	if(dr<tr+s&&dc<tc+s)
		ChessBoard(tr,tc,dr,dc,s);
	else
	{
   
		Board[tr+s-1][tc+s-1]=t;
	    
		//后面几个其实以此类推就行了基本也都是一样的
		//画一个绿色的背景格子
		CClientDC dc(this);
		CBrush pNewBrush(RGB(0,255,0)); 
		CBrush *pOldBrush=dc.SelectObject(&pNewBrush);
		dc.Rectangle((tr+s)*50,(tc+s)*50,(tr+s)*50+50,(tc+s)*50+50);//