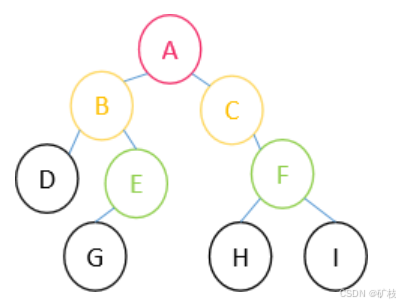
给出一棵二叉树的中序遍历：DBGEACHFI 与后序遍历：DGEBHIFCA ，确定此二叉树的前序遍历。

中序+前后序其中一个才能确定整棵树。以上题为例。

步骤 1: 确定根节点

在后序遍历中，最后一个元素总是树的根节点。因此， A 是这棵树的根节点。

步骤 2: 在中序遍历中找到根节点

在中序遍历 DBGEACHFI 中找到 A ，那么 A 左边的 DBGE 是左子树的中序遍历， CHFI 是右子树的中序遍历。

步骤 3: 在后序遍历中分割左右子树

根据中序遍历中左右子树的元素数量，在后序遍历 DGEBHIFCA 中找到对应的左右子树。左子树的后序遍历是 DGEB ，右子树的后序遍历是 HIFC 。

步骤 4: 递归构建左子树

对于左子树中序遍历 DBGE 和后序遍历 DGEB ：

后序遍历的最后一个元素 B 是左子树的根节点。

在中序遍历 DBGE 中找到 B ，那么 D 是 B 的左子树， GE 是 B 的右子树。

重复步骤3。

步骤 5: 递归构建右子树

对于右子树中序遍历 CHFI 和后序遍历 HIFC ：

后序遍历的最后一个元素 C 是右子树的根节点。

在中序遍历 CHFI 中找到 C ，那么左子树为空， HFI 是 C 的右子树。

重复步骤3。

前序+中序-求后序同理。（注意遍历顺序不一样）