文章目录
前言
上一篇文章我们讨论了yolov3,yolov3在速度与精度上达到了一个较好的平衡,堪称经典之作,可惜在yolov3之后的原作者Joseph Redmon因为yolo的军事应用和对他人个人隐私风险而退出了yolo系列的研究,从此cv界痛失一员大将.但是经典之作总会源远流长,即使yolo原作者Joseph Redmon退出了研究,yolo算法巨大的影响力使得其他的研究者对yolo算法进行进一步讨论研究与发展,由此衍生出yolov3SPP,yolov4,yolov5等等一系列的算法,今天我们要讨论的是yolov4在yolov3的基础上做出的一些改动.v3
PS:如果是小白,建议看一看上一篇yolov3中的相关基础知识.
一、Yolov4网络结构
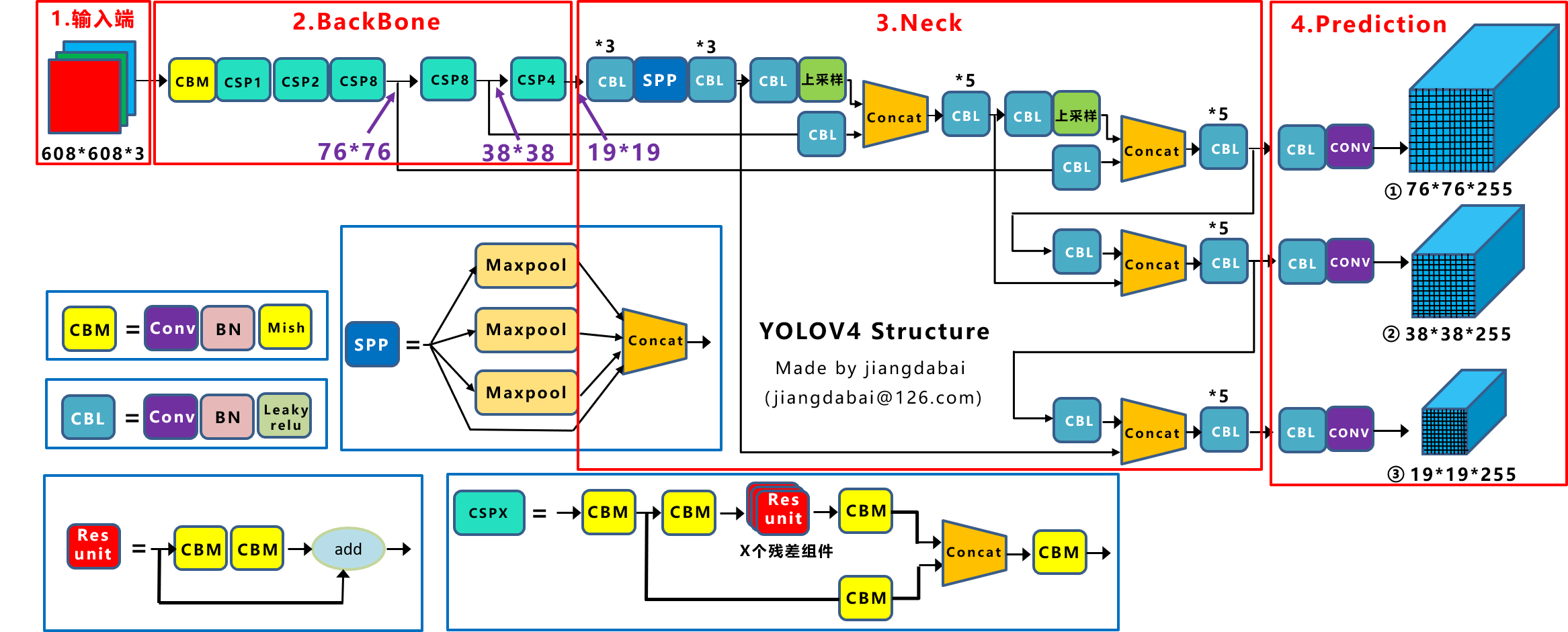
相对于yolov3,yolov4的改动还是比较多的,在网络结构方面主要的改动是修改了Backbone中的残差模块,在backbone后面又添加SPP模块,PAN与Yolo Head模块与yolov3基本一致,话不多说,直接上图.
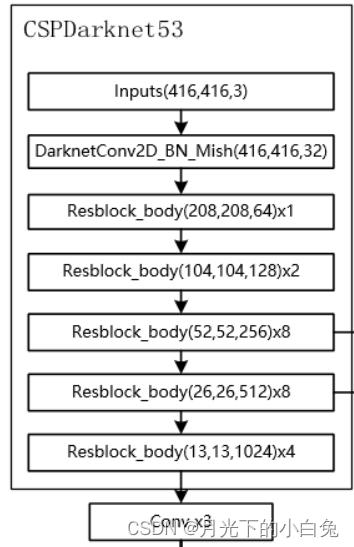
1.backbone:CSP Darknet-53
与Darknet53相比的第一点小改动,残差层之前的2层conv+bn+Relu变成了一层的conv+bn+Mish,主要原因是把Darknet53中残差层之上用来下采样的3x3卷积放入了Resblock_body中.
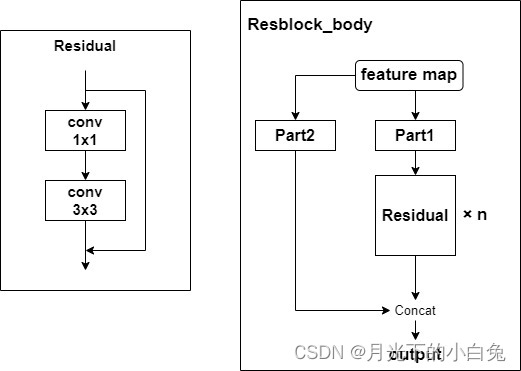
第二点则是对Residual_block的改进,Darknet53中的残差结构与resnet的结构基本相同,但在CSPDarknet53中提出了一种性能更好的残差结构,如下图所示:
对输入的feature map分别进行两次1x1卷积生成Part1与Part2,将Part1输入n个Residual结构中,最后将提取出的特征图与Part2在通道上拼接在一起,每经过一个Resblock_body通道数增加一倍,这种新的残差结构建立了一个大的残差边,这个大的残差边绕过了很多的残差结构,整个CSPDarknet的结构块,可看作一个大的残差块+内部多个小的残差块.
2.SPP池化
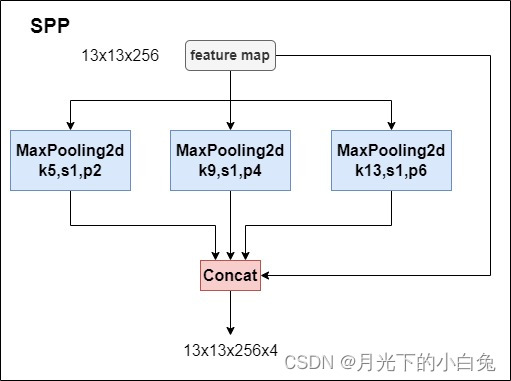
yolov4中新增了SPP池化,它借鉴了SPPnet的结构,但也不是完全相同.具体结构如下图
SPPnet主要解决的问题:
1.有效避免了R-CNN算法对图像区域剪裁、缩放操作导致的图像物体剪裁不全以及形状扭曲等问题
2.解决了卷积神经网络对图像重复特征提取的问题,大大提高了产生候选框的速度,且节省了计算成本。
而yolo中的SPP通过三个不同大小的MaxPooling层进行特征提取,获取到不同感受野大小的三个额外特征图,然后再将得到的特征图拼接在一起,这样使得经过SPP获取得到的特征图具有不同的感受野,特征图包含的信息更全面,另外一方面,Maxpooling层提取kernel_size大小的滑动窗口中最大的值,而上下文语义特征指的是多个相邻的像素点所组成的物体轮廓,个人认为,Maxpooling的滑动窗口提取相邻区域的最大值有一定的特征提取作用,因为都是邻近区域的最大值,所以可能在提取目标轮廓上有一定的促进作用,也就是说,SPP模块可能还增强特征图的上下文特征,但是Maxpooling层的局限性在于丢失大量信息,在使用pooling层还是conv层降图片尺度时我们需要考虑哪一种更适合自己的网络,但最近的很多网络都使用conv代替了pooling,如何减少信息丢失?这是一个值得思考的问题.
3.PAN和Yolo head
PANet对应Neck模块,是FPN的改进版本,FPN主要方法是自顶向下对浅层大尺度特征图进行下采样与深层特征图进行特征融合,输出多个不同尺度的特征图进行预测,PANet在此基础之上增加了对深层特征图的上采样操作,将深层小尺度特征图上采样后concat在一起,提出了一种自顶向下+自底向上的特征融合方式。
PANet可以被看作一个Multiple-input-multiple-output encoder.它对网络性能影响最大的主要有两个方面:
(1) 多尺度特征融合.
(2) 分而治之:简而言之就是输出多个不同尺度具有不同感受野特征图.
对于这两个影响因素谁更重要,可以参考论文YOLOF(You Only Look One-level Feature ),该论文针对提出了一种single-input-single-output的encoder,通过在残差模块中堆叠膨胀卷积使得单级特征图具有更大的感受野,在保证精度的前提下减少了encoder的参数量.
在PAN的论文中特征图融合用的是将两个特征图直接add的方法,但是yolov4中将之改为concat,为什么要改呢?
对于特征图融合的两种方法的理解:
add:将两个特征图直接相加,是resnet中的融合方法,基于这种残差堆叠相加,可以有效地减小因为网络层数加深而导致的cnn网络退化问题.add改变特征图像素值,并没有完全保留原本特征图信息,更多的可以看作对原特征图信息的一种补充,深层特征图在卷积过程中丢失了许多细节信息,通过add的方式得以补全,是在二维的平面上对特征图的增强.因此我认为add在进行图像特征增强时使用最佳.concat:将两个特征图在通道数方向叠加在一起,原特征图信息完全保留下来,再对原特征图增加一些我们认为是较好的特征图,丰富了特征图的多样性,是在空间上对原特征图的增强,这样在下一次卷积的过程中我们能得到更好的特征图.
Yolo head结构与yolov3中基本一致,此处不再多写.
二、改进点
1.Mosaic数据增强
从数据集中随机选取四张图片,进行随机裁剪,缩放,色域变换等等,最后将四张图拼接在一起
作者表示Mosaic数据增强的优点是丰富了检测物体的背景和小目标,并且在计算Batch Normalization的时候一次会计算四张图片的数据,使得mini-batch大小不需要很大,一个GPU就可以达到比较好的效果。
简而言之,当batch_size=1,正常我们只读取1张图片作为训练处理,而Mosaic将4张图片拼接起来使得网络同时处理四张图片,相当于将batch_size放大了4倍,因为图片输入的尺寸不能改变,所以原图片一般都是经过缩小再拼接的,这就导致原本可能大目标的物体变成中目标或者小目标,变相增加了网络训练过程中的小目标数量,因此在检测小目标精度将会得到提升.
2.anchor偏移机制
yolov3中对anchor中心点偏移量
(
t
x
,
t
y
)
(t_x,t_y)
(tx,ty)和先验框缩放量
(
t
w
,
t
h
)
(t_w,t_h)
(tw,th)进行了限制,使得anchor中心点的偏移量在
[
0
,
1
]
[0,1]
[0,1]之间,这样大大减少了anchor中心点偏移过远导致召回率和精度过低.
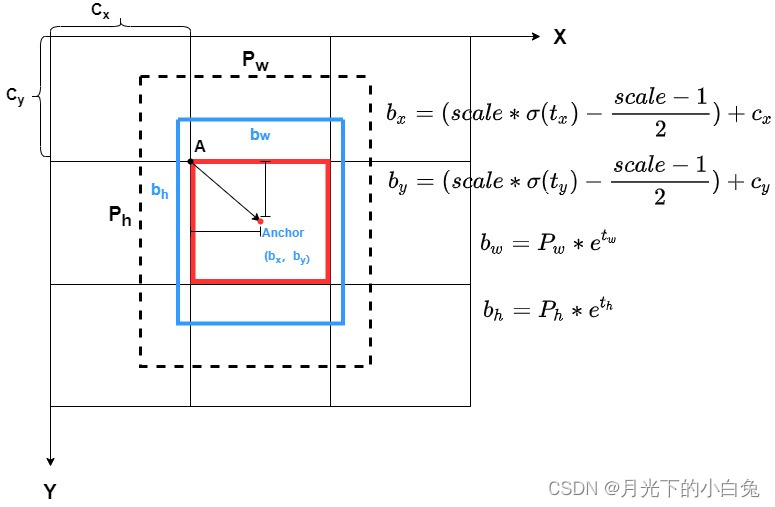
yolov4中考虑了sigmoid函数的局限性,并对anchor中心点偏移量
(
t
x
,
t
y
)
(t_x,t_y)
(tx,ty)的进一步限制,下图所示
(
c
x
,
c
y
c_x,c_y
cx,cy) 网格左上角坐标
(
P
w
,
P
h
P_w,P_h
Pw,Ph) 先验框宽与高
(
b
x
,
b
y
b_x,b_y
bx,by) Anchor最终坐标
(
b
w
,
b
y
b_w,b_y
bw,by) 最终预测框宽与高
由上图可知,yolov4在处理anchor的偏移量(
t
x
,
t
y
t_x,t_y
tx,ty)的公式于yolov3不大一样,因为sigmoid函数在x趋近于
+
∞
+∞
+∞与
−
∞
-∞
−∞的时候才能无限接近于1,这就导致某些中心点在网格顶点的目标无法较好的被预测到,因此我们想到添加一个除了
σ
(
x
)
\sigma(x)
σ(x)之外的限制参数
s
c
a
l
e
scale
scale,使得偏移量的值域增大到1以上,从而使得某些中心点在网格顶点的目标也能得到较好得回归效果.在我们平时搭建网络过程中,
s
c
a
l
e
scale
scale一般取为2的时候效果较好.所以公式可以简化为:
b
x
=
(
2
∗
σ
(
t
x
)
−
0.5
)
+
c
x
b_x =(2*\sigma(t_x)-{0.5})+c_x
bx=(2∗σ(tx)−0.5)+cx
b
y
=
(
2
∗
σ
(
t
y
)
−
0.5
)
+
c
y
b_y =(2*\sigma(t_y)-{0.5})+c_y
by=(2∗σ(ty)−0.5)+cy
b
w
=
P
w
∗
e
t
w
b_w=P_w*e^{t_w}
bw=Pw∗etw
b
h
=
P
h
∗
e
t
h
b_h=P_h*e^{t_h}
bh=Ph∗eth
3.正负样本匹配
针对yolov3的匹配机制导致正样本过少,正负样本匹配不均匀的问题,在匹配正样本的过程之中,在正样本匹配机制上做了以下两点改进:
1. 不再限制一个GT只匹配一个最大iou的anchor template,设定一个阈值,只要anchor template的iou大于这个阈值则判定为正样本
2.(
t
x
,
t
y
t_x,t_y
tx,ty)的值域从[0,1]扩展到了[-0.5,1.5],首先我们计算出GT框的中心点坐标并找到该中心点坐标落 入的网格位置,因此在yolov4中一个GT框可用多个anchor去匹配。
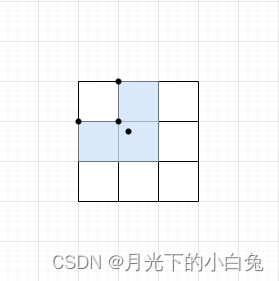
如果GT框中心点落入到网格左上方,相对于左边网格左顶点和上方网格的左顶点而言,该中心点的偏移量在[-0.5,1.5]的范围之内,所以左方和上方的网格皆可为该GT框提供anchor template进行正样本匹配,这样就增加了更多正样本.
同理可知:
如果GT框中心点落入右上,则右方和上方的网格的anchor template也可作正样本匹配,
如果GT框中心点落入左下,则左方和下方的网格的anchor template也可作正样本匹配,
如果GT框中心点落入右下,则右方和下方的网格的anchor template也可作正样本匹配,
还有一种极端情况就是GT中心点正好落入该网格中心点,这时就只需要用这一个网格的anchor template匹配正样本就足够了.
通过这两种方式大大的增加了正样本数量,一定程度上缓解了正负样本匹配不均匀问题.
4.Loss
在学习Loss之前yolov4中还有一个值得说一说的改进点为label smoothing标签平滑 ,给自己数据集打过标签的同学都知道,手动打标签也会存在一定的误差,而在训练过程中我们将标签值设为1,也是会存在一定的误差的,因此我们对标签值设立一个很小很小的惩罚项
ϵ
\epsilon
ϵ,在一定程度上可以平衡手动标签的损失.
yolov4的损失函数改动主要是在定位损失上面,在yolov3的文章中我们已经提到过了
L
o
s
s
l
o
c
Loss_{loc}
Lossloc采用MSE损失函数计算不太合理了,因为一个好的损失函数应该既考虑到预测框与Gt框的宽高损失与中心点损失,还要考虑到iou重合度,个人认为两个框之间的重合度更能反应真实框与预测框之间的差异.
所以yolov4中采用了CIOU来计算定位损失,
L
o
s
s
l
o
c
=
∑
i
∈
p
o
s
(
1
−
c
i
o
u
)
Loss_{loc}=\sum_{i\in pos}(1-ciou)
Lossloc=i∈pos∑(1−ciou)
C
I
O
U
=
I
O
U
−
(
G
T
框与预测框中心点的欧式距离
同时包含预测框和真实框的最小闭包区域的对角线距离
)
−
α
v
CIOU=IOU-( \frac{GT框与预测框中心点的欧式距离}{同时包含预测框和真实框的最小闭包区域的对角线距离})-αv
CIOU=IOU−(同时包含预测框和真实框的最小闭包区域的对角线距离GT框与预测框中心点的欧式距离)−αv
α
=
v
1
−
I
O
U
+
v
α =\frac{v}{1-IOU+v}
α=1−IOU+vv
v
=
4
π
2
∗
(
a
r
c
t
a
n
w
g
t
h
g
t
−
a
r
c
t
a
n
w
h
)
2
v = \frac{4}{\pi ^2}*(arctan\frac{w_{gt}}{h_{gt}}-arctan\frac{w}{h})^2
v=π24∗(arctanhgtwgt−arctanhw)2