《数字图像处理》第三章灰度变换和空间滤波学习笔记附部分例子代码(C++ & opencv)

灰度变换和空间滤波

前言

本系列博客参考书为, 数字图像处理第三版-冈萨雷斯
在这里插入图片描述

第三版教材中图片下载地址： book images downloads

vs2019配置opencv可以查看：VS2019 & Opencv4.5.4配置教程

后续剧情：
数字图像处理第四章频率域滤波学习笔记
 数字图像处理第六章彩色图像处理学习笔记
 数字图像处理第七章小波域多分辨率处理学习笔记
 数字图像处理第九章形态学图像处理学习笔记
 数字图像处理第十章图像分割学习笔记
 数字图像处理第11章表示和描述学习笔记

1. 变换和滤波基础

空间域处理表示为:
$g (x, y) = T [f (x, y)]$
其中f(x, y)是输入图像, g(x, y)是处理后的图像, T是在点(x, y)的邻域上关于f的一中算子.
灰度变换函数: $s = T (r)$ , 其中r是输入图像任意点的灰度, s表示输出后的灰度.

2. 一些基本的灰度变换函数

2.1 图像反转:

$s = L - 1 - r$
适用于增强嵌入在暗区域中的白色或灰色区域
特别是当黑色面积占主导地位.

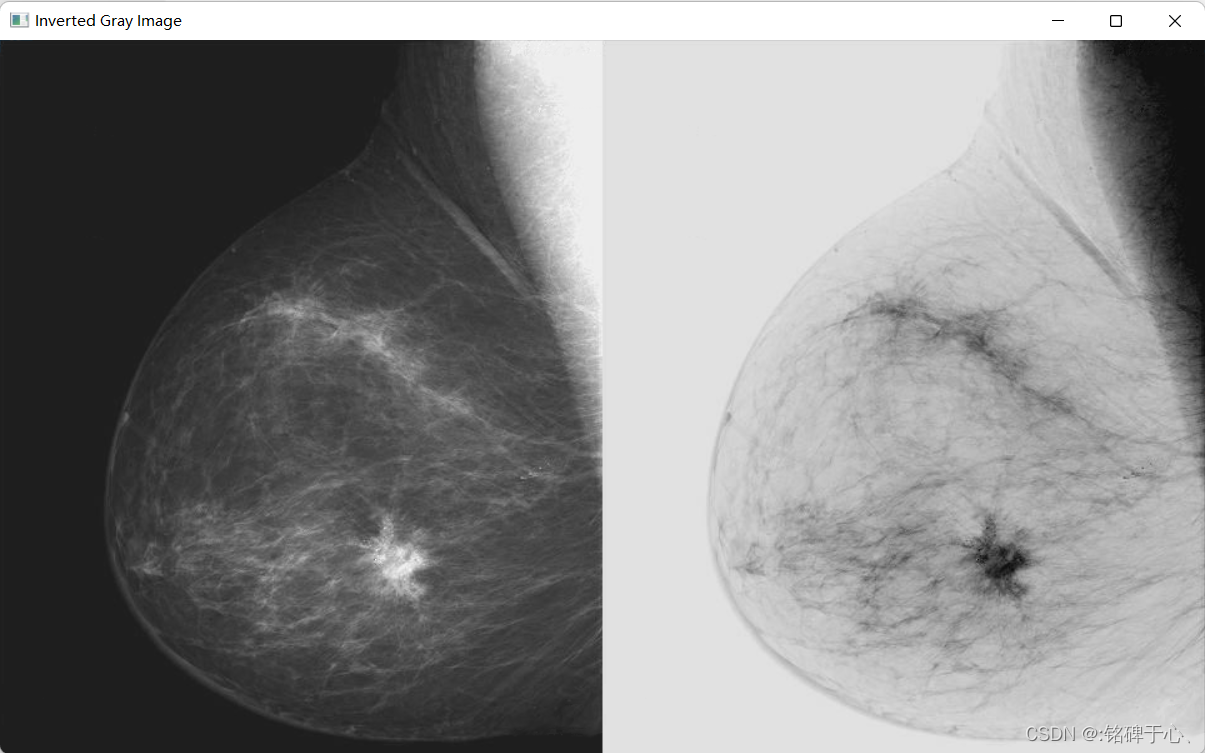
opencv中使用到的是bitwise_not函数

void inversionImage(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cerr << "Could not open or find the image!" << std::endl;
        return;
    }
    Mat in_img;
    bitwise_not(img, in_img);    //图像反转操作, 对应课本的式(3.2-1)

    Mat com_img;
    hconcat(img, in_img, com_img);    //拼接图像

    imshow("Inverted Gray Image", com_img); //输出拼接图像
    waitKey(0);
}

运行结果如下:
请添加图片描述

2.2 对数变换:

$s = c l o g (1 + r)$
完成图像灰度级的扩展或压缩
作用于图像的傅里叶频谱, 会丰富细节

opencv中使用add函数和log函数实现

Mat logTransform(Mat input, int c) {
    //add(input, Scalar(1.0), input);
    input.convertTo(input, CV_32F);

    Mat result;
    log(1.0 + input, result);    //默认以10为底
    //归一化到0-255范围
    normalize(result, result, 0, 255, NORM_MINMAX);
    result = c * result;
    result.convertTo(result, CV_8U);
    return result;
}

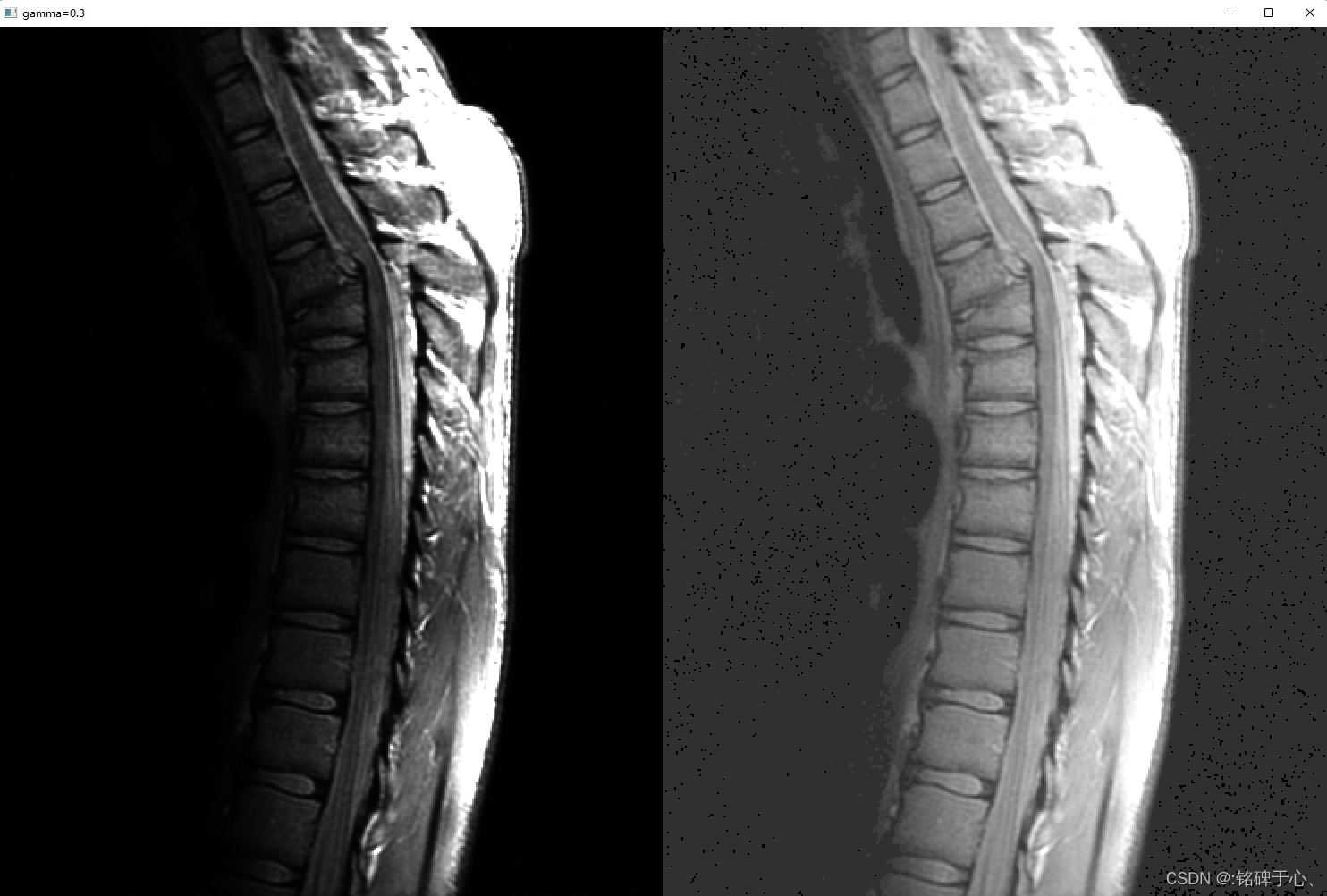
请添加图片描述

2.3 幂律变换:

$s=cr^{γ}$
部分γ值的幂律曲线将较窄范围的暗色输入值映射为较宽范围
用于"伽马校正".
进行对比度增强: 1)对于整体偏暗的图像, 选择伽马值小于1的来完成变换; 2)而对于遭到"冲淡"的图像, 伽马值选择大于1的值.

Mat gammaTransform(Mat input, float gamma, int c) {

    input.convertTo(input, CV_32F);
    Mat result;
    pow(input / 255.0, gamma, result);

    result = c * result;

    normalize(result, result, 0, 255, NORM_MINMAX);
    result.convertTo(result, CV_8U);    //转成uint8格式, 合并操作需要俩图片数据类型一样

    return result;
}

左图, gamma选择0.4, 右图gamma选择4.1; c均选择为1
请添加图片描述

2.4 分段线性变换函数:

对比度拉伸:
灰度级分层:
比特平面分层:

// layerNum的取值范围为1~8
Mat layerTransform(Mat input, uchar layerNum) {
    Mat result;
    uchar bits = 1 << (layerNum - 1);
    result = input & bits;
    result = result * 255;
    return result;
}

请添加图片描述
重构也很简单

Mat layer6 = img & 32;
Mat layer7 = img & 64;
Mat layer8 = img & 128;
Mat reconstract = (layer6 + layer7 + layer8);
imshow("layer6+7+8", reconstract);
waitKey(0);

请添加图片描述

3. 直方图处理

直方图用离散函数表示: $p(r_{k})=n_{k}/MN$ , 其中rk表示第k级灰度值, nk表示图像中灰度为rk的像素个数.
注意: 均值是平均灰度的度量, 方差(或标准差)是图像对比度的度量. 得到直方图, 就能求出这俩个计算的值.

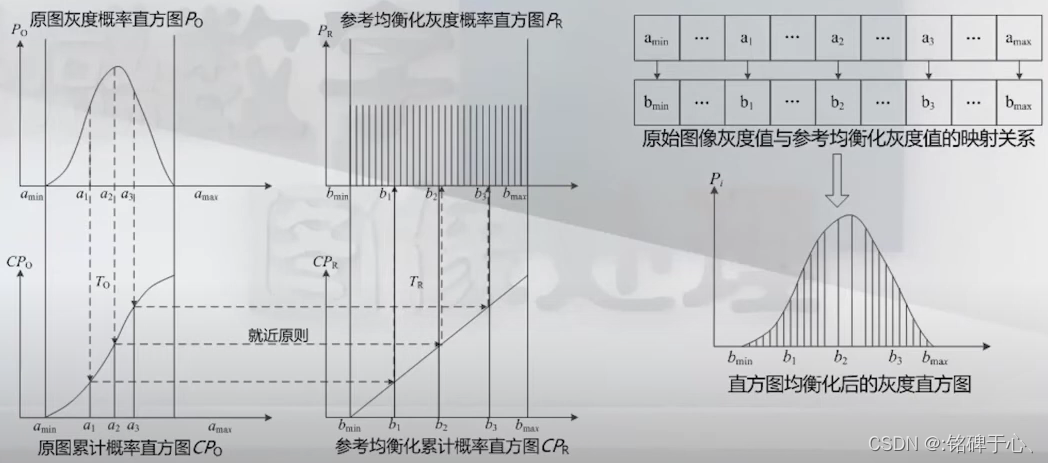
3.1 直方图均衡化

均质化是直方图匹配的一种特殊情况, 对图像重新分配像素值, 使一定范围内的像素值数量大致相同.
优点: 适用于背景和前景都太暗或太亮的图像, 以及曝光过度或曝光不足的图像.
缺点: 可能会增加背景噪声的对比度并且降低有用信号的对比度, 导致对比度过分增强.
原始图和参考图中的灰度累积概率使用就近原则建立关系.

请添加图片描述

均衡化的实现:

如果原图像的灰度值a的累积概率为 $CP_{a}$ , 则该累积概率值所对应的等概率分布图像的灰度值为 $b_{max}-b_{min})×CP_{a} + b_{min}$ , 其中 $b_{max}, b_{min}$ 分别为预期要得到的灰度最大值和最小值.

opencv具体代码实现:

Mat img = imread(path, IMREAD_GRAYSCALE);
Mat result;
equalizeHist(img, result);

Mat com_img;
hconcat(img, result, com_img);    //拼接图像
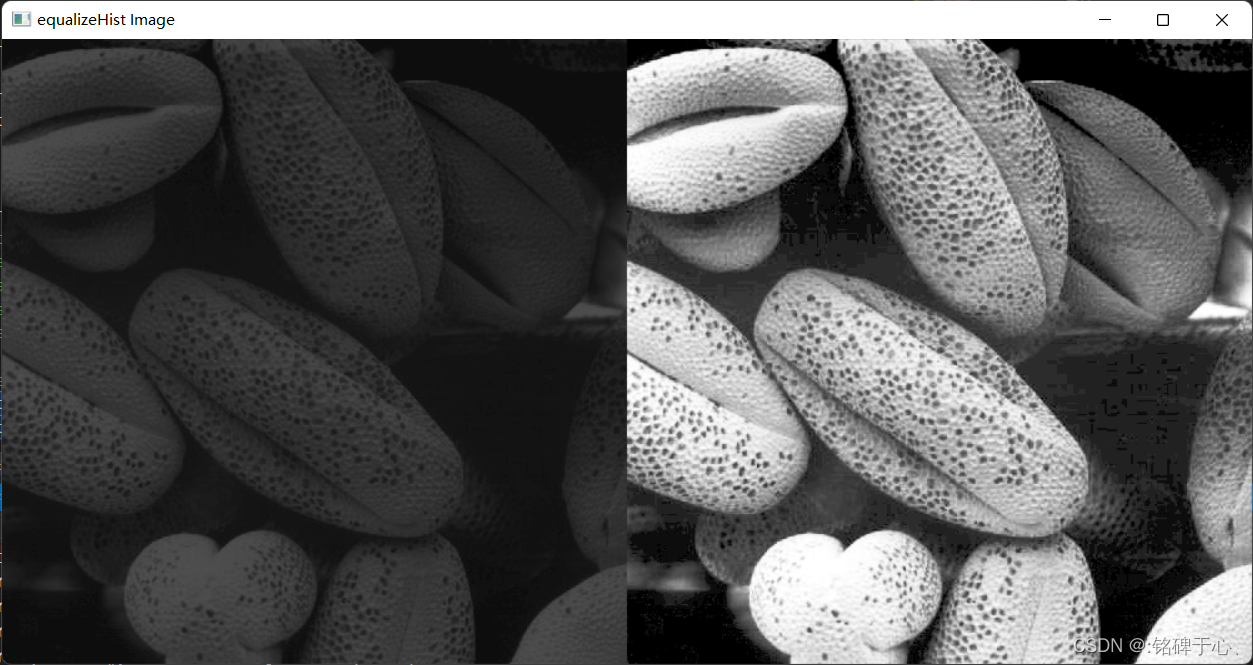
imshow("equalizeHist Image", com_img);
waitKey(0);

请添加图片描述

局部直方图均衡:

Mat localEqualizeHist(Mat input, int blockSize) {
    Mat result = input.clone();
    for (int y = 0; y + blockSize < result.rows; y += blockSize) {
        for (int x = 0; x + blockSize < result.cols; x += blockSize) {
            Mat localImg(result, Rect(x, y, blockSize, blockSize)); //见博客结尾补充第二点
            equalizeHist(localImg, localImg);
        }
    }
    return result;
}

void test(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    Mat histResult;
    equalizeHist(img, histResult);

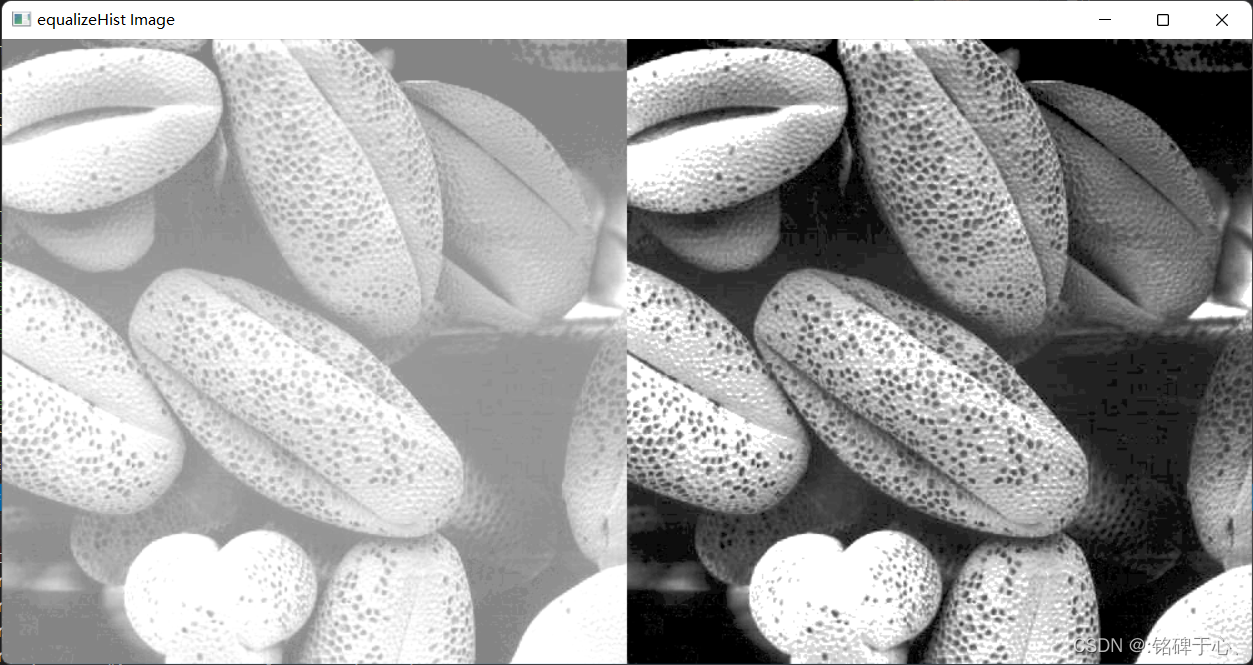
    Mat localHistRes = localEqualizeHist(img, 3);

    Mat comImg;
    hconcat(img, histResult, comImg);    //拼接图像
    hconcat(comImg, localHistRes, comImg);

    imshow("equalizeHist Image", comImg);
    waitKey(0);
}

请添加图片描述

3.2 直方图匹配

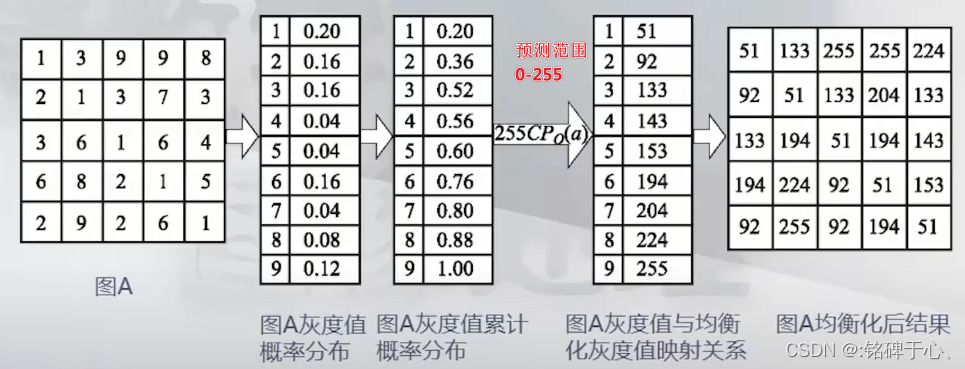
示例: 图A为原始图像, 图B为参考图像
此图演示的是概率值往大的方向就近, 所以图A的"1"与图B的"2"建立联系
直方图匹配大多数时候都是试凑过程.
请添加图片描述

4. 空间滤波基础

4.1 空间滤波原理

滤波产生一个新像素, 新像素的坐标等于邻域中心的坐标, 像素的值是滤波操作的结果.若执行的是线性操作, 则该滤波器称为线性空间滤波器, 反之, 则相反. 滤波器作用的结果主要与滤波器系数和大小有关.
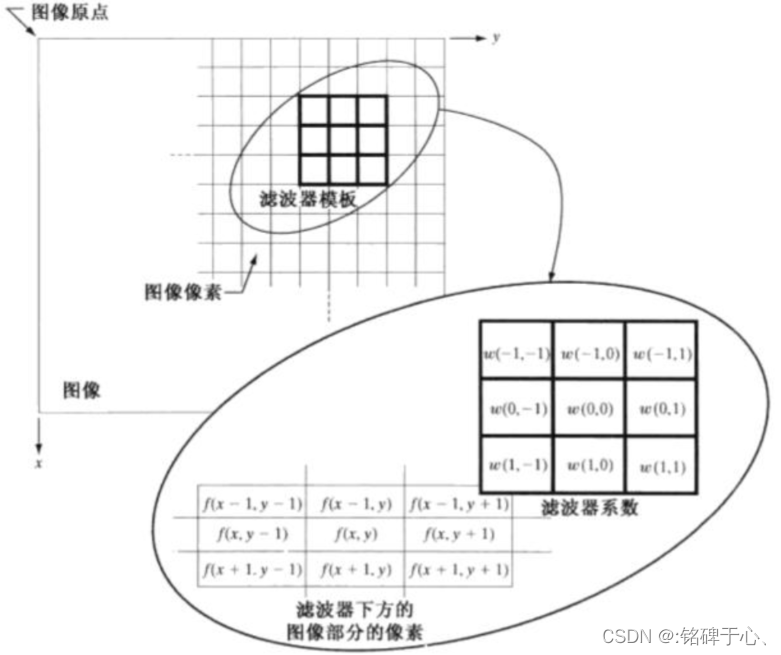
请添加图片描述

4.2 空间相关与卷积

相关: 滤波器模板移过图像并计算每个位置乘积之和的处理.

$w(x,y)☆f(x,y)=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x+s,y+t)$

卷积: 机制类似, 但首先要把滤波器旋转180度.

$w(x,y)★f(x,y)=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x-s,y-t)$

注意: 在图像处理文献中，您很可能会遇到卷积滤波器、卷积模板或卷积核这些术语, 但是这些滤波器未必用到真正的卷积, 要避免混淆.

5. 平滑空间滤波器

通常用于模糊处理和降低噪声.

5.1 平滑线性滤波

opencv实现直接调用blur函数即可.

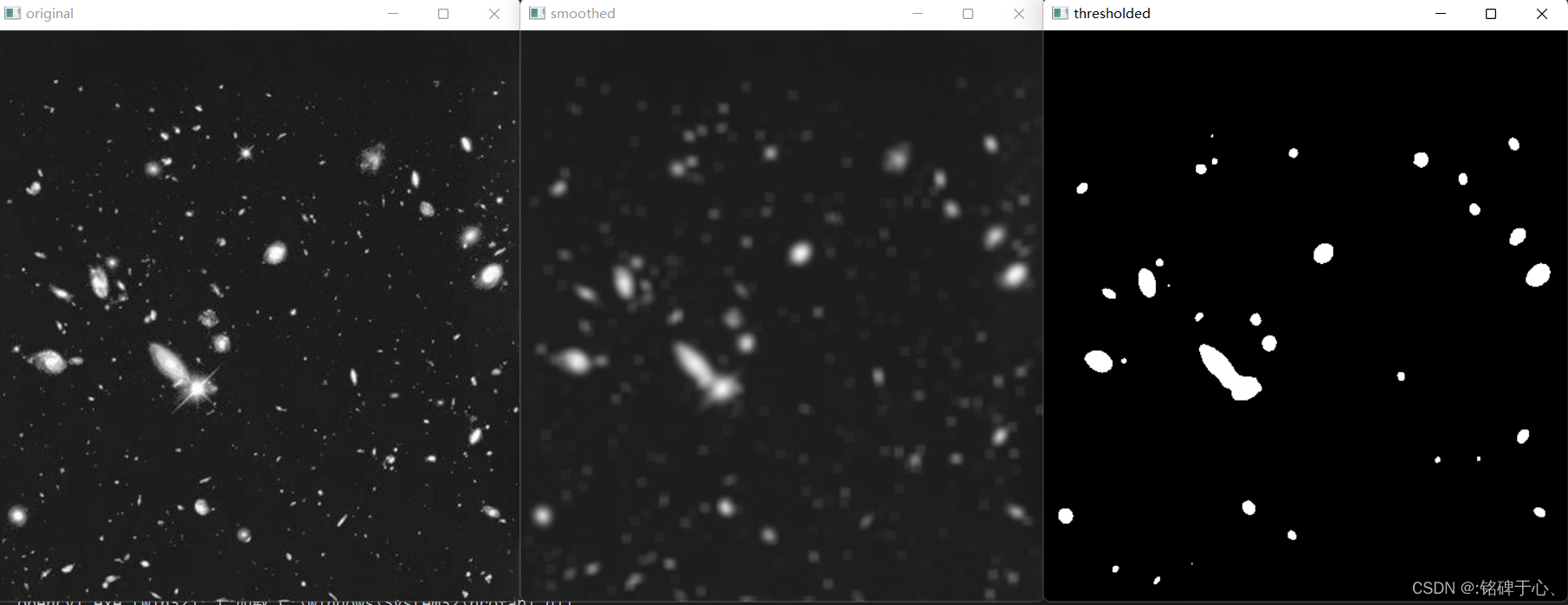
Mat smoothFilter(Mat input, int blockSize) {
	Mat result;
    // 下图使用的滑动块大小为9
	blur(input, result, Size(blockSize, blockSize));
	
	Mat thresholdedImg;
    //表示灰度值大于105的像素设置为255(最大值).
	threshold(result, thresholdedImg, 105, 255, THRESH_BINARY);

	imshow("original", input);
	imshow("smoothed", result);
	imshow("thresholded", thresholdedImg);

	waitKey(0);
	return result;
}

请添加图片描述

5.2 统计排序(非线性)滤波器

本节主要介绍中值滤波器, 该类滤波器对于处理脉冲噪声(椒盐噪声)非常有效. 具体流程为, 首先将邻域内的像素分类排序, 确定其中值, 将该中值赋予滤波后的对应像素点. 例如, 对于3x3的邻域, 中值为第5大的值.
opencv使用medianBlur函数即可, 但注意, 其滤波核的大小必须为奇数.

opencv的补充:

使用cv::Mat::isContinously()来判断图像矩阵是否以连续方式存储
为了避免很大的图像进行不必要的复制, 每个Mat对象都有自己的表头, 复制运算符只复制标头和指向大矩阵的指针, 而不是数据本身.
例: 在一个大图像上创建感兴趣的区域.

Mat D (A, Rect(10, 10, 100, 100) ); //使用矩阵完成
Mat E = A(Range::all(), Range(1,3)); //使用行, 列完成边界
// 此时修改D或E, 同样会修改矩阵A中对应区域的值.