题目
You are playing a very popular Tower Defense game called "Runnerfield 2". In this game, the player sets up defensive towers that attack enemies moving from a certain starting point to the player's base.
You are given a grid of size n×m𝑛×𝑚, on which k𝑘 towers are already placed and a path is laid out through which enemies will move. The cell at the intersection of the x𝑥-th row and the y𝑦-th column is denoted as (x,y)(𝑥,𝑦).
Each second, a tower deals pi𝑝𝑖 units of damage to all enemies within its range. For example, if an enemy is located at cell (x,y)(𝑥,𝑦) and a tower is at (xi,yi)(𝑥𝑖,𝑦𝑖) with a range of r𝑟, then the enemy will take damage of pi𝑝𝑖 if (x−xi)2+(y−yi)2≤r2(𝑥−𝑥𝑖)2+(𝑦−𝑦𝑖)2≤𝑟2.
Enemies move from cell (1,1)(1,1) to cell (n,m)(𝑛,𝑚), visiting each cell of the path exactly once. An enemy instantly moves to an adjacent cell horizontally or vertically, but before doing so, it spends one second in the current cell. If its health becomes zero or less during this second, the enemy can no longer move. The player loses if an enemy reaches cell (n,m)(𝑛,𝑚) and can make one more move.
By default, all towers have a zero range, but the player can set a tower's range to an integer r𝑟 (r>0𝑟>0), in which case the health of all enemies will increase by 3r3𝑟. However, each r𝑟 can only be used for at most one tower.
Suppose an enemy has a base health of hℎ units. If the tower ranges are 22, 44, and 55, then the enemy's health at the start of the path will be h+32+34+35=h+9+81+243=h+333ℎ+32+34+35=ℎ+9+81+243=ℎ+333. The choice of ranges is made once before the appearance of enemies and cannot be changed after the game starts.
Find the maximum amount of base health hℎ for which it is possible to set the ranges so that the player does not lose when an enemy with health hℎ passes through (without considering the additions for tower ranges).
Input
The first line contains an integer t𝑡 (1≤t≤1001≤𝑡≤100) — the number of test cases.
The first line of each test case contains three integers n𝑛, m𝑚, and k𝑘 (2≤n,m≤50,1≤k<n⋅m2≤𝑛,𝑚≤50,1≤𝑘<𝑛⋅𝑚) — the dimensions of the field and the number of towers on it.
The next n𝑛 lines each contain m𝑚 characters — the description of each row of the field, where the character "." denotes an empty cell, and the character "#" denotes a path cell that the enemies will pass through.
Then follow k𝑘 lines — the description of the towers. Each line of description contains three integers xi𝑥𝑖, yi𝑦𝑖, and pi𝑝𝑖 (1≤xi≤n,1≤yi≤m,1≤pi≤5001≤𝑥𝑖≤𝑛,1≤𝑦𝑖≤𝑚,1≤𝑝𝑖≤500) — the coordinates of the tower and its attack parameter. All coordinates correspond to empty cells on the game field, and all pairs (xi,yi)(𝑥𝑖,𝑦𝑖) are pairwise distinct.
It is guaranteed that the sum of n⋅m𝑛⋅𝑚 does not exceed 25002500 for all test cases.
Output
For each test case, output the maximum amount of base health hℎ on a separate line, for which it is possible to set the ranges so that the player does not lose when an enemy with health hℎ passes through (without considering the additions for tower ranges).
If it is impossible to choose ranges even for an enemy with 11 unit of base health, output "0".
题意
有n*m的格子,“#”是敌人会经过的位置,有k个防御装置,有对应的位置和攻击力,对于每个防御装置,每增加r的攻击半径,怪物就会增加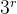
思路
首先,可以发现r的取值不能很大,怪物的血量呈指数上升,稍微打一下表可以发现,r大于13的话就不可能杀死了。
其次,一个防御建筑的有效攻击应该是,它能覆盖到的格子数*它的攻击力-它给怪物增加的血量。
所以现在的问题就变成了,每个防御装置可以选择0-13半径的攻击范围,问最多能产生多少的有效攻击。因为半径的选择范围很小,可以用这一点进行状压dp
首先可以先对每个防御塔,在不同的半径下能产生的有效伤害预处理。
bool check(int x,int y,int p,int q,int r){
return (x-p)*(x-p)+(y-q)*(y-q)<=r*r;
}
for(int i=1;i<=k;i++){
int x,y,w;
cin>>x>>y>>w;
for(int j=0;j<=13;j++){
b[i][j]=0;
for(int p=1;p<=n;p++){
for(int q=1;q<=m;q++){
if(a[p][q]=='.')continue;
if(check(x,y,p,q,j))b[i][j]+=w;;
}
}
}
}定义dp[i][j]为前i个防御塔,用了j状态的半径(二进制的14位表示0-13是否使用),能产生的最多的有效攻击。
转移较为简单
for(int i=1;i<=k;i++){
for(int j=0;j<(1<<14);j++){
dp[i][j]=dp[i-1][j]+b[i][0];
for(int p=1;p<=13;p++){
if((j>>p)&1){
dp[i][j]=max(dp[i][j],dp[i-1][j^(1<<p)]+b[i][p]);
}
}
}
}最后比较每一种状态
#include <bits/stdc++.h>
using namespace std;
#define int long long
char a[55][55];
int dp[3000][1<<13];
int b[10000][20];
bool check(int x,int y,int p,int q,int r){
return (x-p)*(x-p)+(y-q)*(y-q)<=r*r;
}
void solve(){
int n,m,k;
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
cin>>a[i]+1;
}
for(int i=1;i<=k;i++){
int x,y,w;
cin>>x>>y>>w;
for(int j=0;j<=13;j++){
b[i][j]=0;
for(int p=1;p<=n;p++){
for(int q=1;q<=m;q++){
if(a[p][q]=='.')continue;
if(check(x,y,p,q,j))b[i][j]+=w;;
}
}
}
}
for(int i=1;i<=k;i++){
for(int j=0;j<(1<<14);j++){
dp[i][j]=dp[i-1][j]+b[i][0];
for(int p=1;p<=13;p++){
if((j>>p)&1){
dp[i][j]=max(dp[i][j],dp[i-1][j^(1<<p)]+b[i][p]);
}
}
}
}
int ans=0;
for(int i=0;i<(1<<14);i++){
int res=dp[k][i];
int p=1;
for(int j=1;j<=13;j++){
p*=3;
if((i>>j)&1)res-=p;
}
ans=max(ans,res);
}
cout<<ans<<'\n';
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}