什么是堆？

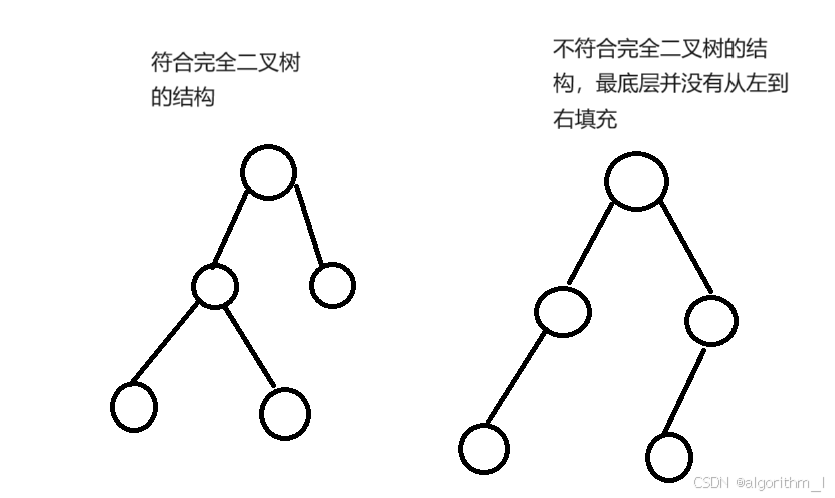
堆可以定义为一棵完全二叉树，且树的节点包含键值，用数组来实现的数据结构。
完全二叉树是指除了最底层，其他每一层都被完全填充，并且在最底层从左到右依次填充。

堆的类型

堆被分为两种类型：
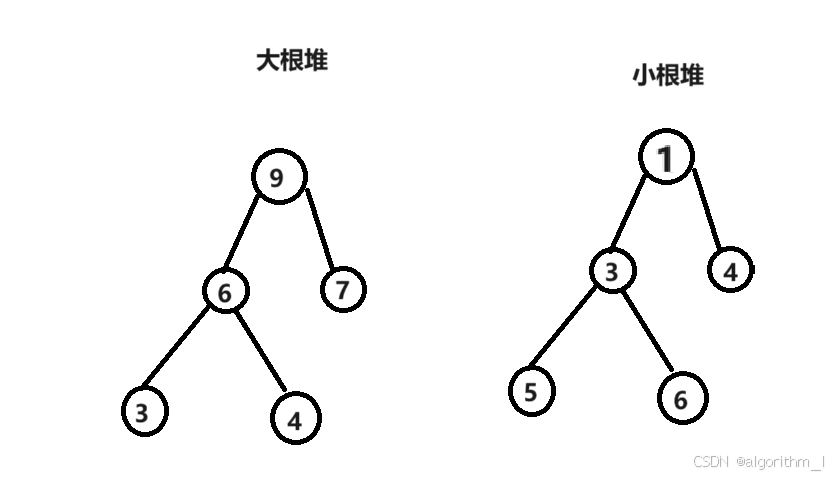
大根堆：对于每个节点 i，父节点的值始终大于或等于其子节点的值。
小根堆：对于每个节点 i，父节点的值始终小于或等于其子节点的值。

这就保证了堆的第一个元素对于大根堆来说一定是所有数的最大值，对于小根堆来说一定是最小值
使得查询最大值（或最小值）的时间复杂度为O(1)。

堆的作用

1.插入一个值
2.输出最小值（小根堆）或最大值（大根堆）
3.删除最小值（小根堆）或最大值（大根堆）
4.删除任意一个数
5.修改任意一个数

如何建堆

对于一开始一堆散乱无序的数据来说，是还不形成堆的，所以要建堆。要建堆的话，就要掌握向下调整的操作了。
向下调整操作是指：如果是小根堆，当父亲节点比最小的孩子节点大时，应该要将父亲节点的值和最小的孩子节点进行交换，一直交换到父亲节点的值小于孩子节点为止（小根堆）
我们拿一组数据模拟一下该过程（在建小根堆的情况下，向下调整的前提是该父亲节点的子树都是小根堆）

1.对于4的节点来说，左子树和右子树都满足了小根堆（父节点大于两个孩子节点），但4大于2，找到最小的孩子节点也就是2，然后对其进行交换，进入第二个过程。
2.4的节点仍然没有满足大于两个孩子节点的条件，所以继续调整，到了最终状态，满足小根堆的条件

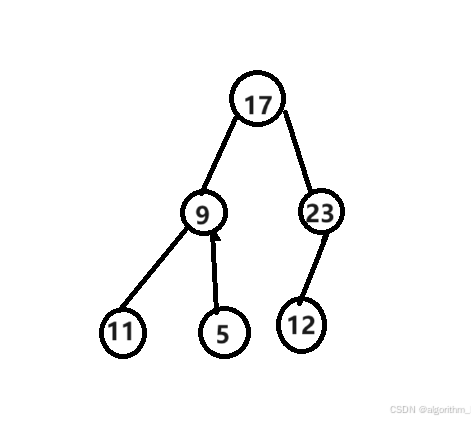
观察这张图，这既不符合小根堆，也不符合大根堆，如果我想让这些数据变成符合小根堆的性质，该如何操作呢。
我们知道堆是数组来实现的，同时堆又是完全二叉树，那就可以用数组下标关系来表示节点之间的父子关系

父亲节点*2=左孩子节点
父亲节点*2+1=右孩子节点（一定要下数据从下标为1开始，不然无法正常查找父子关系）

上面可知，如果要建堆，就要利用向下调整的操作，但无序的数据又不像上面的例子一样，除了根节点以外的左子树和右子树都形成了小根堆。应该要如何操作呢？从上到下的进行多次向下调整不行，那么我们可以先对最后一个父亲节点进行向下调整。

最后一个父亲节点=数据总数n/2

这组数据来说最后一个父亲节点是3=6(数据总数)/2，也就是23的位置。
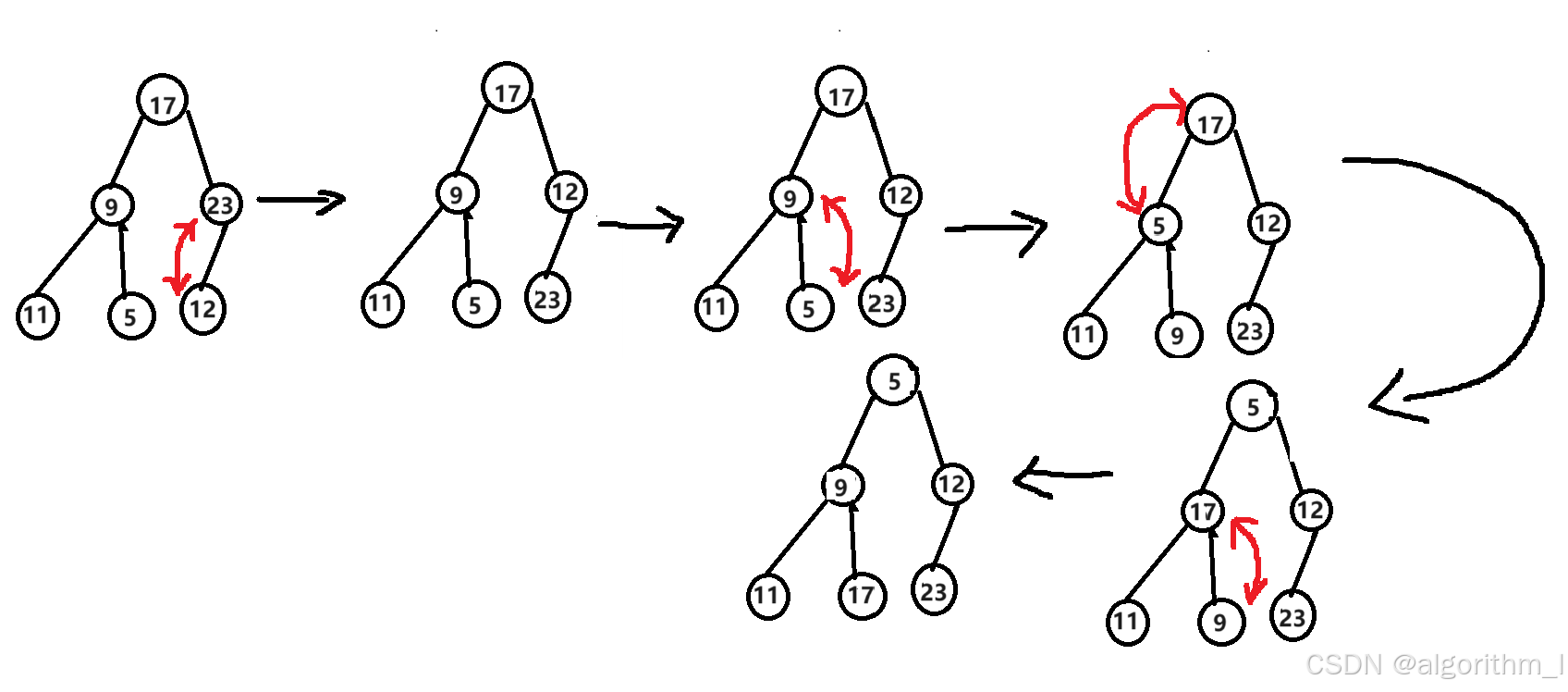
接下来画图分析从最后一个父亲节点向下调整的过程。

从最后一个父母节点往后依次调整，最终将会形成小根堆。

堆的实现

接下来用代码实现建堆，实现一个堆排序的过程吧，这里使用递归和非递归两种方式进行向下调整操作

#include<iostream>
using namespace std;
const int N=1e5+10;
int h[N];//实现堆的数组
int nums;//记录堆中元素个数
int m;//操作次数
void down1(int u){
	//递归做法
	int t=u;
	if(u*2<=nums&&h[t]>h[u*2]) t=u*2;
	//如果左孩子存在，并且父亲节点存储值比左孩子存储值大，t记录左孩子节点
	if(u*2+1<=nums&&h[t]>h[u*2+1]) t=u*2+1;
	//如果右孩子存在，并且上面t节点的存储值比右孩子大，说明找到更小的值了，用t记录该节点
	if(u!=t){
	//说明有孩子并且是存储值最小的孩子节点
	swap(h[u],h[t]);//交换
	down1(t);//让孩子节点作为父亲节点递归交换
	}
}
void down2(int u){
	//	非递归做法
	int c=u*2;//先默认最小的孩子是u*2，也就是左孩子
	while(c<=nums){
	//判断左孩子是否存在
	if(c+1<=nums&&h[c]>h[c+1]) c=c+1;//如果右孩子存在，并且右孩子的值比左孩子更小，就让c记录右孩子
	if(h[u]<h[c]) break; //如果父亲节点的值小于最小的节点了，那么已经符合小根堆的性质，直接跳出循环
	swap(h[u],h[c]);//交换
	u=c;c=u*2;//迭代
} 
}
int main(){
	cin >> nums >> m;
    for(int i=1;i<=nums;i++) scanf("%d",&h[i]);
    for(int i=nums/2;i;i--) down2(i);
    while(m--){
        printf("%d ",h[1]);
        h[1]=h[nums--];
        //输出最小的值后，删掉最小元素，一般是用最后一个元素替代最小值（也就是第一个元素）
        down2(1);//第一个元素再向下调整，找到删除后最小的，也就是第二小，就可以实现排序了
    }
	return 0;
}

接下来我们实现一个模拟堆进行堆的更多操作

这里需要用到插入，插入肯定是在末尾插入的，那么有向下调整的操作，那么一定有向上调整的操作，和向下调整同理，如果孩子节点比父亲节点小，那么需要进行向上调整。
对于这道题而言，题目要求需要删除和修改第k个插入的数，那么我们想要快速找到第k插入个数的下标，就需要开一个数组（下面简称ph[]）记录第k个插入的数的下标。还要开一个数组记录下标对应的是第几个插入的数（下面简称hp[]）。
是为什么呢？
在上面我们说到，向上调整或向下调整都是需要交换值的，那么如果我们要开一个数组ph，在交换值得同时，由于值对应的下标有所改变，那么下标对应的k值一定发生了变化，那么ph里面的值就要发生改变，但如果要改变ph中的值，那我们就要开一个数组来记录下标对应的k值，然后根据这个k值，作为ph的索引，改变两个不同k值对应的下标。（这里有点绕，需要反复理解）

#include<iostream>
using namespace std;
const int N=1e5+10;
int h[N];//数组实现堆
int ph[N];//存放第k个插入的数的下标
int hp[N];//存放某个下标存放着第几个插入的数
int idx;//用来记录是第几个插入的数
int nums;//用来记录堆内有多少数组
int m;//m次操作
void heap_swap(int a,int b){
	swap(hp[a],hp[b]);//先交换a，b两个下标下所指向的idx值（第几个插入的数）
	swap(ph[hp[a]],ph[hp[b]]);//通过hp找到是第几个插入的数，再找到下标，然后改变ph内的值
	swap(h[a],h[b]);
}
void down(int u){
  	int t=u;
	if(u*2<=nums&&h[t]>h[u*2]) t=u*2;
	//如果左孩子存在，并且父亲节点存储值比左孩子存储值大，t记录左孩子节点
	if(u*2+1<=nums&&h[t]>h[u*2+1]) t=u*2+1;
	//如果右孩子存在，并且上面t节点的存储值比右孩子大，说明找到更小的值了，用t记录该节点
	if(u!=t){
	//说明有孩子并且是存储值最小的孩子节点
	heap_swap(u,t);//交换,但不只是简单的值交换
	down(t);//让孩子节点作为父亲节点递归交换
	}
}
void up(int u){
	while(u/2 && h[u] < h[u/2]){
	//直到不再有父亲节点或者已经满足小根堆的性质，停止循环
	heap_swap(u,u/2);
	u=u/2;
}
}
int main(){
  cin >> m;
    while(m--){
        string s;
        cin >> s;
        if(s=="I"){
            int x;
            scanf("%d",&x);
            h[++nums]=x;//先++nums，因为数据要从1开始存储，才能正确表示父子关系
            idx++;
            ph[idx]=nums;hp[nums]=idx;//插入时同时更新hp数组和ph数组
            up(nums);//插入操作只需向上调整
        }
        else if(s=="PM") printf("%d\n",h[1]);
        else if(s=="DM"){
            heap_swap(1,nums);
            nums--;
            down(1);//与上面的堆排序类似，让最后一个值覆盖第一个最小值，删除
        }
        else if(s=="D"){
            int a;
            scanf("%d",&a);
            a=ph[a];//记录第a个插入的数的下标
            heap_swap(a,nums);//删除操作，让最后一个数覆盖要删除的数
            nums--;
            up(a);//向上调整和向下调整只会执行一个，看不满足哪一个性质
            down(a);
        }
        else{
            int a,x;
            scanf("%d%d",&a,&x);
            a=ph[a];
            h[a]=x;
            up(a);
            down(a);
        }

    }
	return 0;
}

STL中的优先队列

STL的优先队列（priority_queue）的底层实现就是堆
在C++中，优先队列默认建大根堆
如果要建小根堆的话
建小根堆声明：priority_queue<int,vector<int>,greater<int>> q;
STL中的堆常用接口函数
push():插入元素
top()：输出最小值（小根堆）或最大值（大根堆）
pop():删除元素

以上是本人对堆的理解，创作不易，如果您从中有收获的话，请您帮我点个赞吧，谢谢啦。如有问题，也可以在评论区一起交流哦。接受一切问题的指出，感谢大家！