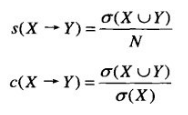关联分析:FP-Growth算法
关联分析又称关联挖掘,就是在交易数据、关系数据或其他信息载体中,查找存在于项目集合或对象集合之间的频繁模式、关联、相关性或因果结构。关联分析的一个典型例子是购物篮分析。通过发现顾客放入购物篮中不同商品之间的联系,分析顾客的购买习惯。比如,67%的顾客在购买尿布的同时也会购买啤酒。通过了解哪些商品频繁地被顾客同时购买,可以帮助零售商制定营销策略。关联分析也可以应用于其他领域,如生物信息学、医疗诊断、网页挖掘和科学数据分析等。
1. 问题定义
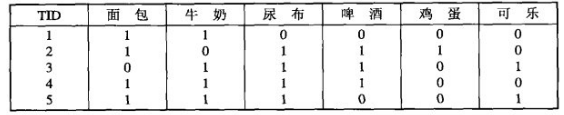
图1 购物篮数据的二元表示
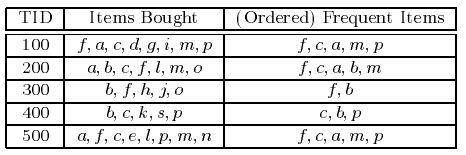
图1表示顾客的购物篮数据,其中每一行是每位顾客的购物记录,对应一个事务,而每一列对应一个项。令I={i1, i2, … , id}是购物篮数据中所有项的集合,而T={t1, t2, … , tN}是所有事务的集合。每个事务ti包含的项集都是I的子集。在关联分析中,包含0个或多个项的集合被称为项集(itemset)。所谓的关联规则是指形如X→Y的表达式,其中X和Y是不相交的项集。在关联分析中,有两个重要的概念——支持度(support)和置信度(confidence)。支持度确定规则可以用于给定数据集的频繁程度,而置信度确定Y在包含X的事务中出现的频繁程度。支持度(s)和置信度(c)这两种度量的形式定义如下:
公式1
其中,N是事务的总数。关联规则的支持度很低,说明该规则只是偶然出现,没有多大意义。另一方面,置信度可以度量通过关联规则进行推理的可靠性。因此,大多数关联分析算法采用的策略是:
(1)频繁项集产生:其目标是发现满足最小支持度阈值的所有项集,这些项集称作频繁项集。
(2)规则的产生:其目标是从上一步发现的频繁项集中提取所有高置信度的规则,这些规则称作强规则。
2. 构建FP-tree
FP-growth算法通过构建FP-tree来压缩事务数据库中的信息,从而更加有效地产生频繁项集。FP-tree其实是一棵前缀树,按支持度降序排列,支持度越高的频繁项离根节点越近,从而使得更多的频繁项可以共享前缀。
图2 事务型数据库
图2表示用于购物篮分析的事务型数据库。其中,a,b,…,p分别表示客户购买的物品。首先,对该事务型数据库进行一次扫描,计算每一行记录中各种物品的支持度,然后按照支持度降序排列,仅保留频繁项集,剔除那些低于支持度阈值的项,这里支持度阈值取3,从而得到<(f:4),(c:4),(a:3),(b:3),(m:3,(p:3)>(由于支持度计算公式中的N是不变的,所以仅需要比较公式中的分子)。图2中的第3列展示了排序后的结果。
FP-tree的根节点为null,不表示任何项。接下来,对事务型数据库进行第二次扫描,从而开始构建FP-tree:
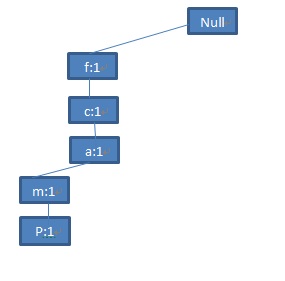
第一条记录<f,c,a,m,p>对应于FP-tree中的第一条分支<(f:1),(c:1),(a:1),(m:1),(p:1)>:
图3 第一条记录
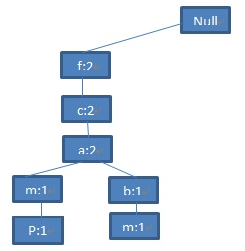
由于第二条记录<f,c,a,b,m>与第一条记录有相同的前缀<f,c,a>,因此<f,c,a>的支持度分别加一,同时在(a:2)节点下添加节点(b:1),(m:1)。所以,FP-tree中的第二条分支是<(f:2),(c:2),(a:2),(h:1),(m:1)>:
图4 第二条记录
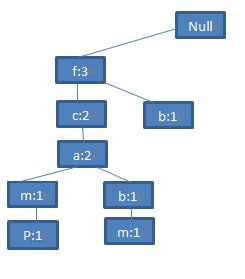
第三条记录<f,b>与前两条记录相比,只有一个共同前缀<f>,因此,只需要在(f:3)下添加节点<b:1>:
图5 第三条记录
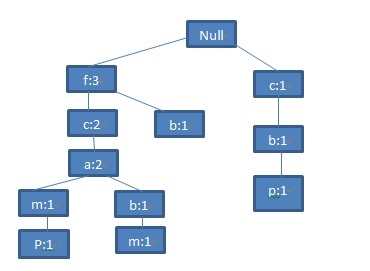
第四条记录<c,b,p>与之前所有记录都没有共同前缀,因此在根节点下添加节点(c:1),(b:1),(p:1):
图6 第四条记录
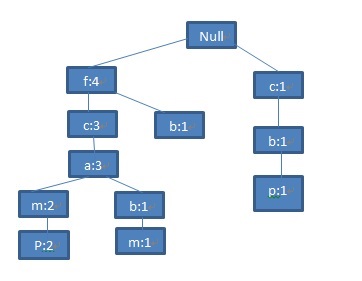
类似地,将第五条记录<f,c,a,m,p>作为FP-tree的一个分支,更新相关节点的支持度:
图7 第五条记录
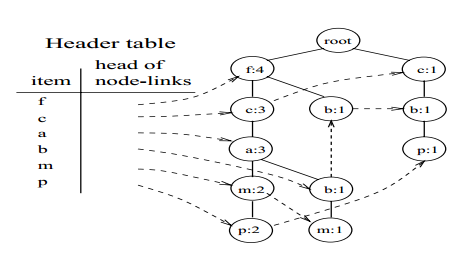
为了便于对整棵树进行遍历,建立一张项的头表(an item header table)。这张表的第一列是按照降序排列的频繁项。第二列是指向该频繁项在FP-tree中节点位置的指针。FP-tree中每一个节点还有一个指针,用于指向相同名称的节点:
图8 FP-tree
综上,FP-tree的节点可以定义为:
|
1
2
3
4
5
6
7
8
9
10
11
|
class
TreeNode {
private
:
String name;
// 节点名称
int
count;
// 支持度计数
TreeNode *parent;
// 父节点
Vector<TreeNode *> children;
// 子节点
TreeNode *nextHomonym;
// 指向同名节点
...
}
|
3. 从FP-tree中挖掘频繁模式(Frequent Patterns)
我们从头表的底部开始挖掘FP-tree中的频繁模式。在FP-tree中以p结尾的节点链共有两条,分别是<(f:4),(c:3),(a:3),(m:2),(p:2)>和<(c:1),(b:1),(p:1)>。其中,第一条节点链表表示客户购买的物品清单<f,c,a,m,p>在数据库中共出现了两次。需要注意到是,尽管<f,c,a>在第一条节点链中出现了3次,单个物品<f>出现了4次,但是它们与p一起出现只有2次,所以在条件FP-tree中将<(f:4),(c:3),(a:3),(m:2),(p:2)>记为<(f:2),(c:2),(a:2),(m:2),(p:2)>。同理,第二条节点链表示客户购买的物品清单<c,b,p>在数据库中只出现了一次。我们将p的前缀节点链<(f:2),(c:2),(a:2),(m:2)>和<(c:1),(b:1)>称为p的条件模式基(conditional pattern base)。我们将p的条件模式基作为新的事务数据库,每一行存储p的一个前缀节点链,根据第二节中构建FP-tree的过程,计算每一行记录中各种物品的支持度,然后按照支持度降序排列,仅保留频繁项集,剔除那些低于支持度阈值的项,建立一棵新的FP-tree,这棵树被称之为p的条件FP-tree:
图9 p的条件FP-tree
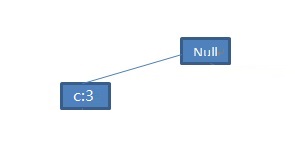
从图9可以看到p的条件FP-tree中满足支持度阈值的只剩下一个节点(c:3),所以以p结尾的频繁项集有(p:3),(cp:3)。由于c的条件模式基为空,所以不需要构建c的条件FP-tree。
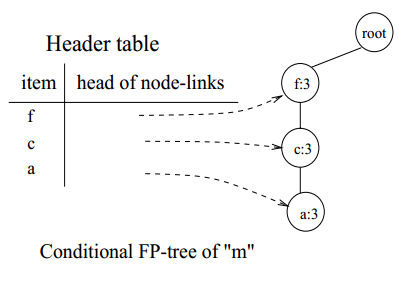
在FP-tree中以m结尾的节点链共有两条,分别是<(f:4),(c:3),(a:3),(m:2)>和<(f:4),(c:3),(a:3),(b:1),(m:1)>。所以m的条件模式基是<(f:2),(c:2),(a:2)>和<(f:1),(c:1),(a:1),(b:1)>。我们将m的条件模式基作为新的事务数据库,每一行存储m的一个前缀节点链,计算每一行记录中各种物品的支持度,然后按照支持度降序排列,仅保留频繁项集,剔除那些低于支持度阈值的项,建立m的条件FP-tree:
图10 m的条件FP-tree
与p不同,m的条件FP-tree中有3个节点,所以需要多次递归地挖掘频繁项集mine(<(f:3),(c:3),(a:3)|(m:3)>)。按照<(a:3),(c:3),(f:3)>的顺序递归调用mine(<(f:3),(c:3)|a,m>),mine(<(f:3)|c,m>),mine(null|f,m)。由于(m:3)满足支持度阈值要求,所以以m结尾的频繁项集有{(m:3)}。
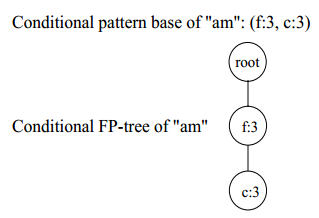
图11 节点(a,m)的条件FP-tree
从图11可以看出,节点(a,m)的条件FP-tree有2个节点,需要进一步递归调用mine(<(f:3)|c,a,m>)和mine(<null|f,a,m>)。进一步递归mine(<(f:3)|c,a,m>)生成mine(<null|f,c,a,m>)。因此,以(a,m)结尾的频繁项集有{(am:3),(fam:3),(cam:3),(fcam:3)}。
图 12 节点(c,m)的条件FP-tree
从图12可以看出,节点(c,m)的条件FP-tree只有1个节点,所以只需要递归调用mine(<null|f,c,m>)。因此,以(c,m)结尾的频繁项集有{(cm:3),(fcm:3)}。同理,以(f,m)结尾的频繁项集有{(fm:3)}。
在FP-tree中以b结尾的节点链共有三条,分别是<(f:4),(c:3),(a:3),(b:1)>,<(f:4),(b:1)>和<(c:1),(b:1)>。由于节点b的条件模式基<(f:1),(c:1),(a:1)>,<(f:1)>和<(c:1)>都不满足支持度阈值,所以不需要再递归。因此,以b结尾的频繁项集只有(b:3)。
同理可得,以a结尾的频繁项集{(fa:3),(ca:3),(fca:3),(a:3)},以c结尾的频繁项集{(fc:3),(c:4)},以f结尾的频繁项集{(f:4)}。
4. 算法实现
声明FP-tree节点:
class TreeNode
{
//Constructors-Destructors
public:
TreeNode();
TreeNode(string);
~TreeNode();
//Member variables
private:
string nodeName;
int supportCount;
TreeNode *parentNode;
vector<TreeNode *> childNodeList;
TreeNode *nextHomonymNode;
//Member functions
public:
string getName();
void setName(string);
int getSupportCount() const;
void setSupportCount(int);
TreeNode* getParentNode() const;
void setParentNode(TreeNode*);
vector<TreeNode*> getChildNodeList() const;
void addChild(TreeNode*);
TreeNode* findChildNode(string) const;
void setChildren(vector<TreeNode*>);
void printChildrenNames() const;
TreeNode* getNextHomonym() const;
void setNextHomonym(TreeNode *nextHomonym);
void countIncrement(int);
};
构建HeaderTable:
//HeaderTable存储事务数据库的数据
vector<TreeNode*> FPTree::buildHeaderTable(vector<vector<string>> transRecords)
{
vector<TreeNode*> F1; //存储满足支持度阈值的节点,并按照支持度降序排列,支持度相等的情况下按照字母顺序排序,所以构建的FP-tree与论文有所不同,但是最终生成的频繁项集是一样的
if (transRecords.size() > 0)
{
map<string, TreeNode*> mp;
//calculate supportCount of every transRecords
for (vector<string> record : transRecords)
{
for (string item : record)
{
//if item not in map, put item into map and set supportCount one
if (mp.find(item) == mp.end())
{
TreeNode *node = new TreeNode(item);
node->setSupportCount(1);
mp.insert(map<string, TreeNode*>::value_type(item, node));
}
//if item in map, supportCount plus one
else
{
mp.find(item)->second->countIncrement(1);
}
}
}
//put TreeNodes whose supportCount greater than minSupportThreshold into vector F1
for (auto iterator = mp.begin(); iterator != mp.end(); iterator++)
{
if (iterator->second->getSupportCount() >= minSupportThreshold)
{
//cout << "iterator->second = " << iterator->second->getSupportCount() << endl;
F1.push_back(iterator->second);
}
}
//sort vector F1 by supportCount
sort(F1.begin(), F1.end(), sortBySupportCount);
}
return F1;
}
构建FP-tree:
TreeNode* FPTree::buildTree(vector<vector<string>> transRecords, vector<TreeNode*> F1)
{
TreeNode *root = new TreeNode(); //根节点root
for (vector<string> transRecord : transRecords)
{
//拷贝transRecord到record
vector<string> record;
for (auto iter = transRecord.begin(); iter != transRecord.end(); iter++)
{
record.push_back(*iter);
}
record = sortedByF1(record, F1); //根据F1中存储的频繁项集,将record按照支持度降序排列,并且仅保留频繁项集,剔除那些低于支持度阈值的项
//顺序比较record中的节点和FP-tree中的节点,如果record中的节点已经存在于FP-tree中,将该节点的支持度加一,继续比较下一个节点,否则调用addNodes来添加剩余节点到FP-tree中
TreeNode *subTreeRoot = root;
TreeNode *tmpRoot = nullptr;
if (!root->getChildNodeList().empty())
{
while (!record.empty() && (tmpRoot = subTreeRoot->findChildNode(*(record.begin()))) != nullptr)
{
tmpRoot->countIncrement(1);
subTreeRoot = tmpRoot;
record.erase(record.begin());
}
}
addNodes(subTreeRoot, &record, F1);
}
return root;
}
添加节点:
void FPTree::addNodes(TreeNode *ancestor, vector<string> *record, vector<TreeNode*> F1)
{
if (!record->empty())
{
while (!record->empty())
{
string item = *(record->begin());
record->erase(record->begin());
TreeNode *leafNode = new TreeNode(item);
leafNode->setSupportCount(1);
leafNode->setParentNode(ancestor);
ancestor->addChild(leafNode);
for (TreeNode *f1 : F1)
{
if (f1->getName() == item)
{
while (f1->getNextHomonym() != NULL)
{
f1 = f1->getNextHomonym();
}
f1->setNextHomonym(leafNode);
break;
}
}
addNodes(leafNode, record, F1);
}
}
}
sortedByF1:
vector<string> FPTree::sortedByF1(vector<string> transRecord, vector<TreeNode*> F1)
{
//如果item是频繁项,则一定对应于F1中的序号,按照该序号对item进行排序,存储到rest中
map<string, int> mp;
for (string item : transRecord)
{
for (int i = 0; i < F1.size(); i++)
{
TreeNode *tNode = F1[i];
if (tNode->getName() == item)
{
mp.insert(map<string, int>::value_type(item, i));
}
}
}
vector<pair<string, int>> vec;
for (auto iterator = mp.begin(); iterator != mp.end(); iterator++)
{
vec.push_back(make_pair(iterator->first, iterator->second));
}
sort(vec.begin(), vec.end(), sortByF1);
vector<string> rest;
for (auto iterator = vec.begin(); iterator != vec.end(); iterator++)
{
rest.push_back((*iterator).first);
}
return rest;
}
递归调用FP-Growth挖掘频繁项:
//postPattern存储后缀,比如从HeaderTable中的p节点开始挖掘频繁项时,postPattern为p
void FPTree::FPGrowth(vector<vector<string>> transRecords, vector<string> postPattern)
{
vector<TreeNode*> headerTable = buildHeaderTable(transRecords); //构建headerTable
TreeNode *treeRoot = buildTree(transRecords, headerTable); //构建FP-tree
//递归退出条件:根节点没有孩子节点
if (treeRoot->getChildNodeList().size() == 0)
{
return;
}
//输出频繁项集
if (!postPattern.empty())
{
for (TreeNode *header : headerTable)
{
cout << header->getSupportCount() << ends << header->getName() << ends;
for (string str : postPattern)
{
cout << str << ends;
}
cout << endl;
}
}
//遍历headerTable
for (TreeNode *header : headerTable)
{
vector<string> newPostPattern;
newPostPattern.push_back(header->getName());
//存储原先的后缀
if (!postPattern.empty())
{
for (string str : postPattern)
{
newPostPattern.push_back(str);
}
}
//newTransRecords存储前缀节点链
vector<vector<string>> newTransRecords;
TreeNode *backNode = header->getNextHomonym();
//通过getNextHomonym遍历同名节点,通过getParentNode获取前缀节点链
while (backNode != nullptr)
{
int supportCount = backNode->getSupportCount();
vector<string> preNodes;
TreeNode *parent = backNode;
while ((parent = parent->getParentNode())->getName().length() != 0)
{
preNodes.push_back(parent->getName());
} while (supportCount-- > 0)
{
newTransRecords.push_back(preNodes);
}
backNode = backNode->getNextHomonym();
}
FPGrowth(newTransRecords, newPostPattern); //递归构建条件FP-tree
}
}
5. 讨论
在韩家炜教授提出FP-growth算法之前,关联分析普遍采用Apriori及其变形算法。但是,Apriori及其变形算法需要多次扫描数据库,并需要生成指数级的候选项集,性能并不理想。FP-growth算法提出利用了高效的数据结构FP-tree,不再需要多次扫描数据库,同时也不再需要生成大量的候选项。
对于单路径的FP-tree其实不需要递归,通过排列组合可以直接生成。韩家炜教授在其论文中提到了针对单路径的优化算法。论文中也提到了面对大数据时,如何调整FP-growth算法使之适应数据量。