目录
6.3 向量点乘公式3,如果都是单位向量,那么A·B = cos θ
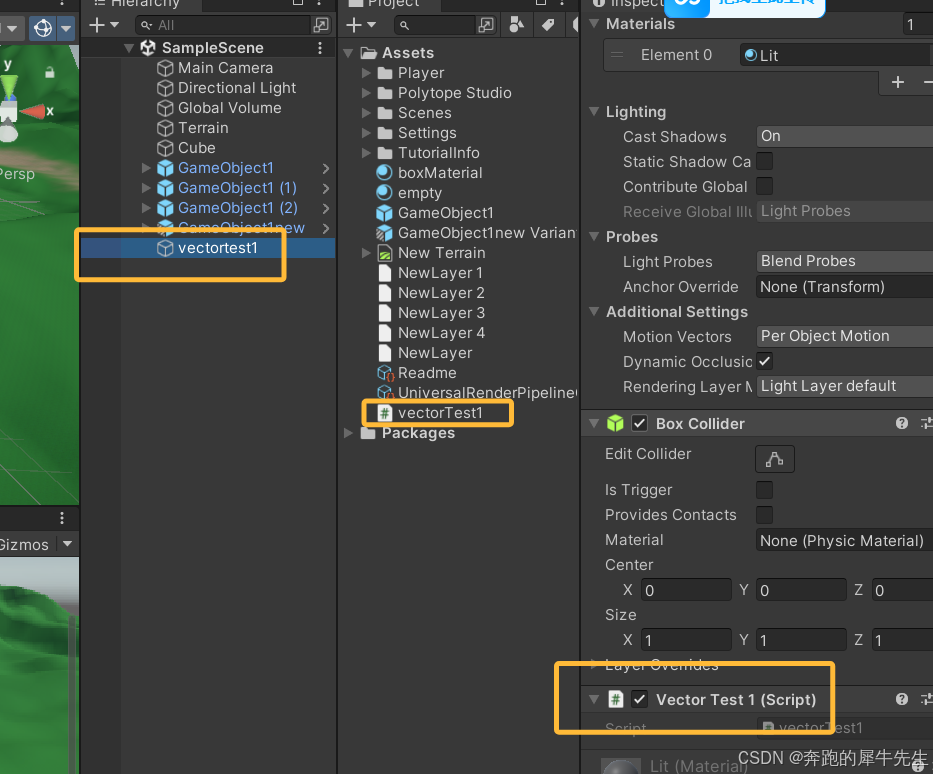
8.0 unity里的C#脚本新建以后,必须挂到bierarcry下才会生效
8.1 结构体vector 有几种, 虽然有多个数,但是还不是矩阵, 都还是向量vector
8.2 vector3 在unity里,可以是向量,坐标,旋转方向,缩放比例等
8.5.1 可以显示 Vector3结构体变量的某个维度坐标
8.5.2 可以显示 Vector3结构体变量的其他属性(变量本身的方法属性一般不大写首字母)
8.6 unity里2个向量的一些计算(Vector3.方法,大写首字母)
1 unity里的向量:
- 一般坐标原点(0,0,0) 到某个点(x,y,z) 指向的一个有方向的线段
- 起点:坐标原点的坐标:zero(0,0,0)
- 终点:箭头的坐标
- 一般的向量都是从原点出发的,也有其他不从原点出发的向量
- 起点:起点的坐标
- 终点:箭头的坐标
2 向量加法
2.1 向量加法的几何意义
- 平行四边形法
- 把一个向量接在另外一个向量的箭头(尾部)得到的点,(从原点出发)形成的新向量
2.2向量加法的标量算法
- 向量的加法,可以转化为标量的计算
- 因为向量,本身是以终点的坐标来表示的,加法也可以用这个坐标的3个维度的标量直接计算即可
- A+B=(xa+xb), (ya+yb) ,(za+zb)
3 向量减法
3.1 向量减法的几何意义
- 三角形法
- 从被减的向量的尾部箭头,往减去它的向量的尾部箭头,连线+方向,(注意不是从原点生成的,而是直接生成了起点和终点,)形成的新向量即是减法的结果。
3.2 向量减法的标量算法
- 向量的减法,可以转化为标量的计算
- 因为向量,本身是以终点的坐标来表示的,减法也可以用这个坐标的3个维度的标量直接计算即可
- A-B=(xa-xb), (ya-yb) ,(za-zb)
4 向量的标量乘法
- a是标量
- aA(x,y,z)= (ax,ay,az)
5 向量之间的乘法要注意是左乘 还是右乘
5.1 注意区别
- A*B != B*A
5.2 向量,矩阵,张量,还是要注意区分,不要随便混用
- 向量相乘,矩阵相乘,其实是不一样的
- 虽然向量可以看成是1维的矩阵,但一般还是把矩阵认为至少是二维的
- 1维的: vector 向量
- 2维的: matrix 矩阵
- 3维+的: tensor 张量
6 向量的点乘 / 点积
- A·B =x1*y1+x2*y2
- 为什么呢
- 因为这里是说的向量的点乘
- 肯定需要两个向量可以进行乘法,所以肯定是一个横向量,1个总向量T
- 因此所得结果才是一个标量
- A*B = (x1,x2)*(y1,y2)T= (x1y1+x2*y2)
6.1 向量点乘公式1
- A*B = (x1,x2)*(y1,y2)T= (x1y1+x2*y2)
- 得到的结果是一个标量
6.2 向量点乘公式2
- A·B =|A| · |B| · cos θ
- 得到的结果是一个标量
6.3 向量点乘公式3,如果都是单位向量,那么A·B = cos θ
- A·B =|A| · |B| · cos θ
- 如果把AB,标准化为单位向量,那么|A|=1 · |B| =1
- A·B = cos θ
- 又因为 cos y = x 那么 y=arccos x
- 这样可以直接求出 θ
- 为什么可以标准化为单位向量后,来计算 夹角 θ
- 因为本身2个向量之间的夹角θ 也和两个向量本身的长度无关
- 所以直接拿到A,B对应的 单位向量即可
6.4 向量点乘的几何意义
- A·B =|A| · |B| · cos θ
- 其实就是一个向量A,往另外一个向量B的方向上进行投影,形成的新A*cos θ ,与B 相乘的结果。 结果是1个标量,没有方向
7 向量的叉乘
向量的叉乘结果还是1个向量
7.1 向量叉乘的几何意义
- AxB 就是他们法线方向投影形成的一个新向量
- AxB ,其实就是一个向量A,往另外一个向量B的法线(正交)方向上进行投影,形成的新A*sin θ ,与B 相乘的结果 , 计算结果是一个新向量
8 unity里的 多种向量 vector
8.0 unity里的C#脚本新建以后,必须挂到bierarcry下才会生效
8.1 结构体vector 有几种, 虽然有多个数,但是还不是矩阵, 都还是向量vector
- vector2 2维的, (x,y) 描述3维的向量
- vector3 3维的, (x,y,z) 描述3维的向量
- vector4 四元数, (x,y,z,w) 描述4维的向量
- 注意:矩阵是这样的,matrix = [[1,2],[1,2]]
8.2 vector3 在unity里,可以是向量,坐标,旋转方向,缩放比例等
- 向量: Vector3 v=new Vector3(1,1,0.5f);
- 坐标: Vector3 v=new Vector3(1,1,0.5f);
- 旋转: Vector3 v=new Vector3(1,1,0.5f);
- 缩放: Vector3 v=new Vector3(1,1,0.5f);
8.3 结构体的初始化方法有两种
- new
- v=Vector3.zero;
8.3.1 用new,new一个新的实例除了
- Vector3 v=new Vector3(1,1,0.5f);
- 类型 变量名 = new 类名(参数)
8.3.2 直接变量=特定的固定/内置属性
- v=Vector3.zero;
- 变量= Vector3.zero
- 变量= Quaternion.identity
8.4 特殊的vector,系统封装好后可以直接用
- v=Vector3.zero;
- v=Vector3.one;
- v=Vector3.forward; //同坐标轴的3个方向的单位向量, z方向,(0,0,1)
- v=Vector3.right; //同坐标轴的3个方向的单位向量, x方向,(1,0,0)
- v=Vector3.up; //同坐标轴的3个方向的单位向量,x方向,(0,1,0)
可以直接改变V的各个坐标值
- v.x=0;
- v.y=0;
- v.z=0;
8.5 unity里单个向量的一些计算
8.5.1 可以显示 Vector3结构体变量的某个维度坐标
- Debug.Log(v1.x+v1.y+v1.z);
- Debug.Log() 同时只能显示1个
8.5.2 可以显示 Vector3结构体变量的其他属性(变量本身的方法属性一般不大写首字母)
- 显示其长度:模,v1.magnitude
- 讲其标准化, v1.normalized
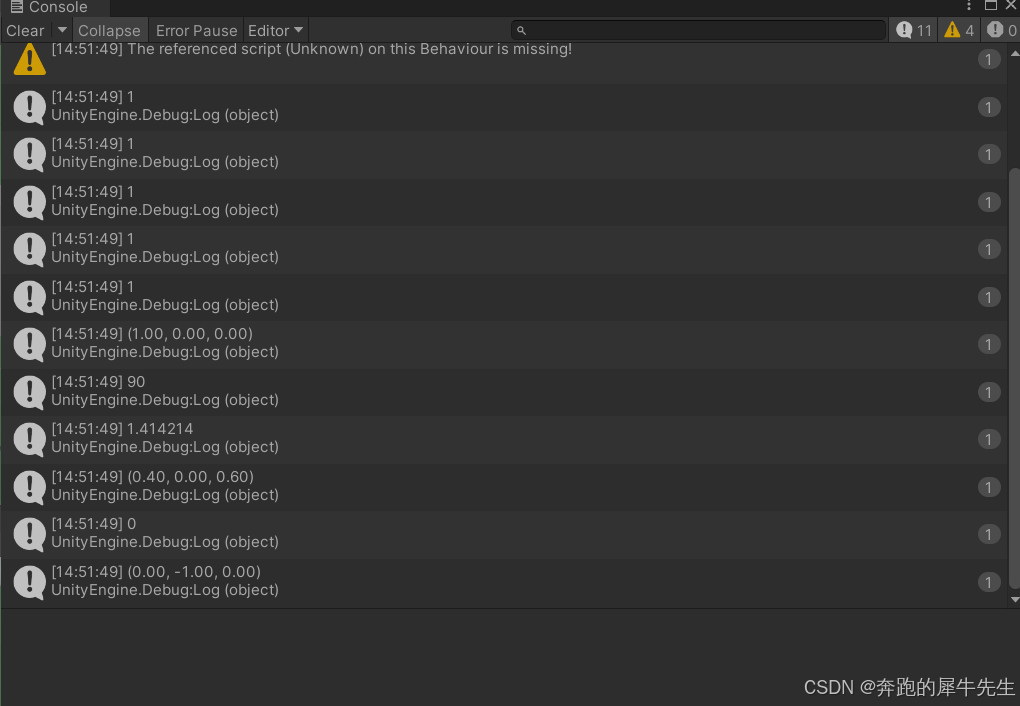
8.6 unity里2个向量的一些计算(Vector3.方法,大写首字母)
- 计算2个向量之间的夹角
- 包装的方法内部就是用点乘算出来的
- Vector3.Angle(v1,v2)
- 计算2个向量之间的距离
- Vector3.Distance(v1,v2)
- 计算2个向量之间的lerp插值
- Vector3.Lerp(v1,v2,0.6f)
- 计算2个向量之间的点乘
- Vector3.Dot(v1,v2)
- 计算2个向量之间的叉乘
- Vector3.Cross(v1,v2)
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class vectorTest1 : MonoBehaviour
{
// Start is called before the first frame update
void Start()
{
Vector3 v1=Vector3.right;
Debug.Log(v1.x+v1.y+v1.z);
Vector3 v2=Vector3.forward;
Debug.Log(v2.x+v2.y+v2.z);
Vector3 v3=Vector3.up;
Debug.Log(v3.x+v3.y+v3.z);
//计算1个向量之间的属性
Debug.Log(v1.x+v1.y+v1.z);
Debug.Log(v1.magnitude);
Debug.Log(v1.normalized);
//计算2个向量之间的夹角
Debug.Log(Vector3.Angle(v1,v2));
//计算2个向量之间的距离
Debug.Log(Vector3.Distance(v1,v2));
//计算2个向量之间的lerp插值
Debug.Log(Vector3.Lerp(v1,v2,0.6f));
//计算2个向量之间的点乘
Debug.Log(Vector3.Dot(v1,v2));
//计算2个向量之间的叉乘
Debug.Log(Vector3.Cross(v1,v2));
}
// Update is called once per frame
void Update()
{
}
}